ĐẠI SỐ SƠ CẤP_ÔN THI ĐẠI HỌC
-
Upload
le-ngoc-son -
Category
Documents
-
view
459 -
download
0
Transcript of ĐẠI SỐ SƠ CẤP_ÔN THI ĐẠI HỌC
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 1/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 1 -
TÀI LIỆU ÔN THI ĐẠI HỌC
(Đại số sơ cấp)
PHẦN I: PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
Phương trình và bất phương trình bậc 2, 2( 0;ax bx c a .
Câu 1: Tìm m để phương trình: 2 2( 3) 4 12 0x m x m có hai nghiệm cùng lớn hơn -1.
Giải
Để pt đã cho có hai nghiệm cùng lớn hơn -1 thì m thỏa mãn hệ sau:
' 2
1 2
0 ( 3) 4 12 07
1. ( 1) 0 1 2( 3) 4 12 0 3.2
1 31
2
m m
f m m m
x x m
Câu 2: Tìm a để BPT: (1)
2
( 1) 2( 2) 2 1 0a x a x a , có nghiệm trong ( 1,2). Giải
Xét ba trường hợp của a như sau
TH1:1
1; (1) 6 3 0 .2
a x x (thỏa mãn)
TH2: 1;a ta có
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 2/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 2 -
2'
2 2
1
2 2
2
2
5 3 5 5 3 55 5 00 2 2
2 ( 2) 5 5 2( 1) 5 5 3
1 ( 2) 5 5 ( 1) 5 5 3
5 3 5 5 3 5
2 2
5 5 3 .
1 4
a a a
x a a a a a a a
x a a a a a a
a
a a a
a
(VN)
TH3:
1a
+ ' 0 (1; ).a
'
2 21
2 2 2
5 3 5 5 3 5 5 3 5 5 3 50
2 2 2 21
1( 1) ( 2) 5 5 3 5 52
2( 1) ( 2) 5 5 3 5 5
5 3 5 5 3 52 2( ; 1 / 2) (1
a a
x a a a a a a
x a a a a a a a
a
a
5 3 5( ; 1 / 2).2; )
a
Câu 3: Tìm m để pt: [ ]+ 2 2 0x x x x m , có hai nghiệm không âm. ([x] là phần nguyên của x).
Giải
Đặt [ ] [ ];y x z x x , ta có, 2 2 0,z z y y m trong đó y nguyên và 0 1.z
Pt theo z có nghiệm1
2z
, với 21 4( )y y m , vì 0z nên
1
2z
và
10 1
2z
hay 21 9 0 2.y y m
Gọi1 2
x x là hai nghiệm không âm của pt, ta có [ ] [ ]1 1 2 2
;y x y x đều không âm, và
[ ]; [ ].1 1 1 2 2 2
z x x z x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 3/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 3 -
- Nếu1 2
y y thì [ ] [ ]1 2
x x và [ ]+ [ ]+2 2
1 1 1 1 2 2 2 22 0; 2 0x x x x m x x x x m , trừ vế
theo vế ta được1 2
x x (trái với GT)
- Nếu1 2 1 2
1y y y y (do số nguyên).
Vì 2 2 2
1 1 2 2 2 20 2;0 2 2 0(*)y y m y y m y y m nên
2 2 2 2
1 2 2 1 1 2 2 1 1 2 1 22 2 | | 2 ( ) | 1 | 2,y y y y y y y y y y y y Vì
1 2y y
là số nguyên dương nên 1 2
1 2
| 1 | 1
| 1 | 0
y y
y y
- TH1:1 2 1 2 1 2
| 1 | 1 2 2; 0y y y y y y (không thỏa)
-
TH2: [ ] [ ]1 2 1 2 1 2 1 2| 1 | 0 1 1; 0 1; 0y y y y y y x x
Từ (*) suy ra: 0 2m và nghiệm1,2
1 1 4
2
m x
.
Câu 4. Tìm ĐK của a,b để pt: 2 1 0 (1);x ax x bx có nghiệm chung. Khi
đó tìm GTNN của | | | | .P a b
Giải
- Gọi0
x là nghiệm chung của hai pt trên, ta có,
2
0
2
0
.x ax
a b x x a bx bx a b
Thế vào (1) ta được :
2
2
2 2 2 2
1 11 0 1 ( ) ( ) 0
2 3 1 0 3 2 1 0
a a a b a ba b a b
a ab b ab a b
Vậy điều kiện của a,b là 2 23 2 1
a b
ab a b
thì pt có hai chung.
- Ta có | | | |P a b , thế vào điều kiện trên ta được2 2 2 23 | || | 2 | | | | 1 6 1 5 | | 0a b a b a P a P
Để pt luôn có nghiệm thì
2 2
24 0 24 | | 2 6P P P Min P
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 4/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 4 -
Phương trình và bất pt quy về bậc hai
Ví dụ 1. Tìm m để pt : ( )x m x mx m , cos 3 nghiệm phân biệt thỏa mãn
1 2 3.1 2x x x
Giải
pt (1) đã có 1 nghiệm x m nên pt x mx m phải có haio nghiệm phân biệtthảo một trong các TH sau :
- TH1 :1 2
1 2 .m x x
- TH2 :1 2
1 2 .x m x
- TH3 :1 2
1 2 .x x m
- Xét TH1 :1 2 1 2
1 2
11 1. ( 1) 0
1 2 11
2 21. (2) 0
m
m f
m x x x x S
x x f
(VN)
- Xét TH2 :
2'
21 2
1
22
2 11 2
2 3 00 11 2 2 .
1 2 3 1 6
2 2 3 2
m m
m m x m x m
x m m m
x m m m
- Xét TH3 :
2
'
1 2
1 2
1 2
22 22 3 0
0 11 2 1. ( 1) 0
1 61. (2) 0 22
22
m m m
m m
x x m f m x x
f m x x
S
(VN)
- Vậy với 126
m thì pt (1) có 3 nghiệm thỏa mãn1 2 3
1 2 .x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 5/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 5 -
Ví dụ 2. Tìm m để pt : 3 23 3 2 0x mx x m có 3 nghiệm thỏa mãn1 2 3.
1 2x x x
giải
Xét hàm số3 2 2
( ) 3 3 2 ; '( ) 3 6 f x x mx x m f x x mx m
- pt '( ) 0 f x luôn có hai nghiệm phân biệt nen hs luôn có CĐ, CT. Giả sử1 2
x x là hai
nghiệm của pt '( ) 0 f x , khi đó :
2 2
1 1 2 2
2 2 2 2
1 2 1 2
2(1 ) ; 2(1 )
. 2(1 ) 2(1 ) 4 7 4 0,
y m x m y m x m
y y m x m m x m m m m
- Suy ra, pt đã cho luôn có ba nghiệm1 2 3
x x x
- Vì1 2
1 0x x nên pt luôn có 2 nghiệm trái dấu. Để pt có nghiệm thỏa mãn ĐKBT thì
2( 1) 0 2 0 12.1(2) 0 10 2 0 5
5
m f m m
f m m
Bài 1. Biện luận theo m số nghiệm của pt : (1).( 1)( 2)( 3) 1 0x x x x m
Giải
Pt 1 2 2 2 2 2( 3 )( 3 2) 1 0 ( 3 ) 2( 3 ) 1 0.x x x x m x x x x m
Đặt 2 9( 3 ), .
4t x x t
Pt quay trở về : (2);2 '2 1 0 .t t m m
- TH1 : ' 0 0m , Pt có 2 nghiệm PB
+ Nếu9 25
14 16
m m thì pt (2) có 2 nghiệm PB dẫn đến pt (1) có 4 nghiệm PB.
+ Nếu9 25
14 16
m m thì pt (2) có 1 nghiệm đẫn đến pt (1) có 2 nghiệm PB.
- TH2 : ' 0 0m , pt (2) có nghiệm kép 1t , dẫn đén pt (1) có 2 nghiệm phân
biệt.
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 6/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 6 -
- TH3 : ' 0 0m , pt (2) vô nghiệm dẫn đến pt (1) vô nghiệm.
Bài 2. Tìm a để pt : 416ax ax a x ax cos 4 nghiệm PB lập thành
một cấp số nhân.
Giải
Nhận thấy 0x không là nghiệm của pt (1), chia hai vế pt (1) cho 2x ta được
2
2
1 116 2 17 0x a x a
x x
, đặt
1;| | 2t x t
x , ta có :
216 2 15 0t at a
Để pt (1) có 4 nghiệm PB thì pt (2) phait có 2 nghiệm phân biệt thỏa mãn1 2
| |,| | 2.t t Gọi
1 2 3 4, , ,x x x x là 4 nghiệm lập thành một CSN của pt (1), ta có
1 4,x x là hai nghiệm của pt :
2
11 0x t x , và
2 3;x x là hai nghiệm của pt 2
21 0x t x , gọi q là công bội ta có,
2 3 3 3
2 1 3 1 4 1 1 4 1 1 1 3
2 23 2 2 3 2 2 2
1. ; . ; . . 1 . ;
11 .
x x q x x q x x q x x x q x q x q
x x q x x x q x q x q
Vậy 3
1 2 3 43
1 1; ; ;x x x q x q
q q .
Theo ĐL Viét ta có,
3
31 2 3 4
21 2 1 3 1 2 2 4 3 4 2
1 1
16
1 1 2 171 1
16
a b q q x x x x q
q a c a x x x x x x x x x x q q
a q q
Đặt1
;| | 2t q t q
ta được
3
4 3 2
4 2
2 1516 2 3 4 02 15 16
316
a t t
t t t t a
t t
PT này có nghiệm : 3 5 1 2; ;2 2 2
t t t vì | | 2t nên 5 85 170.2 16 8
a t a
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 7/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 7 -
BÀI TẬP
Bài 1. Biết PT 227 12 2001 0ax x x có ba nghiệm PB. Tính số nghiệm của PT :
2
4( 27 12 2001)(3 27) (3 .ax x x ax ax x
Giải
Đặt2 2( ) 27 12 2001 '( ) 3 54 12 ''( ) 6 54 2(3 27) f x ax x x f x ax x f x ax ax
Pt quy về : [ ]22 ( ). ''( ) '( ) f x f x f x .
Đặt [ ]2( ) 2 ( ). ''( ) '( ) '( ) 2 ( ). '''( ).g x f x f x f x g x f x f x
Gọi1 2 3
x x x là nghiệm của pt : ( ) 0 f x , suy ra
2
1 2 3 1 2 3( ) ( )( )( ) '( ) 12 ( )( )( ) f x a x x x x x x g x a x x x x x x , vậy '( ) 0g x
cũng có 3 nghiệm PB1 2 3, ,x x x do đó hs g x đạt cực trị tại ba điểm. Ta có
[ ]
[ ]
[ ]
2
1 1
2
2 2
2
3 3
( ) '( ) 0
( ) '( ) 0 ( ) 0
( ) '( ) 0
g x f x
g x f x g x
g x f x
có hai nghiệm PB
1. Phương trình và bất pt chứa căn
Bài 1. Giải bất pt :1 1 1
1x
x x x x
(1).
ĐK :
2 10 1 0 1
1 0 1.0 11
0
x x x
x x x x x x
x
- Với 1x ;
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 8/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 8 -
-
22
2
2
2
( 1)1 1 1 1 1 1(1)
11 1 ( 1) 1 ( 1) 1
( 1) 1 2 ( 1) ( 1) 2 ( 1) 1 0 ( ( 1) 1) 0
1 5 1 5( 1) 1 1 0 ( 1)
2 2
x x x x x x x
x x x x x x
x x x x x x x x x x
x x x x x x x x x x x x x
x x x x x x x
- Với 1 0x
2
2
2
(1 )1 1 1 1
(1) 1 1( )
( 1) 1 ( 1) 1
( 1) 1 2 (1 ) (1 ) 2 (1 ) 1 0
( (1 ) 1) 0 ( )
x x x x x
x x x x x
x x x x x x x x
x x x x x x x x x x
x x VN
Vậy bất pt có nghiệm là :1 5
1;2
x x
.
Bài 2. Giải bất pt :2
1 1 2 (1)4
x x x
Giải
ĐK : 1 1x
22 42
2 2
2 22 2 2 2 2
22
(1) 1 1 2 2 2 1 44 16
2(1 1 ) (1 ) 2(1 1 )(1 1 ) (1 )(1 1 )16 16
(1 )(1 1 )16
x x x x x x
x x x x x x x x
x x x x
+ x là một nghiệm của (*).
+ Khi 0x ,
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 9/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 9 -
(ñuùng vôùi moïi
2 22 2 2
22 2 2
22 2
2
22 2 2
2
2 (1 )(1 1 ) 2 1 1 (1 1 )16 16
1 1 (1 1 )161 1 (1 1 ) 0 0
16 (1 1 )
(1 1 )16 0 0)
(1 1 )
x x x x x
x x x
x x x
x
x x x
x x
Vậy tập nghiệm của bất pt là [ 1;1].S
Bài 2. Giải pt (1)2
2 3 3 2 11 1 (1 ) (1 )
33
x x x x
Giải
- Với 1 0x
3 3
2 3 3
1 1 (1 ) (1 )
1 1 (1 ) (1 ) 0 (1) .
x x x x
x x x V N
- Với 0 1x , đặt os( );0 .2
x c t t
3 2 sin(1) 1 sin (1 cos ) cos
3
sinsin cos cos sin
sin cos cos sin sin cos sin cos
t t t t
t t t t t
t t t t t t t t
cos cos
cos sin
cos
t t t t
t x
Bài 3. Giải pt (1)6 10
42 3x x
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 10/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 10 -
Đặt
2 2
2 2 2
2
22 2 2 4 3 22
2
3 2
60.
2
10 10 10(1) 4 4 4
2 6 6 63
0 40 4 0 4
1010 (4 ) ( 6) 8 12 48 96 0(4 )
60 4 0 4
2( 2)( 6 48) 0
t x
t t t t t
t t t
t
t t t
t t t t t t t t t
t
t t
t t t t
(vì
Vôùi
3 2( 6 48) 0).
6 6 12 2 4 .
2 2 2
t t
t x
x x
Bài 4. Giải pt (1)32 2 23 37 8 6 7 2 3 12 3x x x x x x
Giải
- Đặt 32 2 23 37 8; 6 7; 2 3 12t x x u x x v x x
(1) 3t u v
- Ta có,
Khi töùc laø
Khi töù
3 3 3 3 3 3 3 3
2 2
2 2
32 23
27 ( ) ( )
( ) ( ) ( ) ( ) 0
( )( ) ( )( ) 0
( )( )( ) 0
7 5 56 7 2 3 12 ,
2
t u v t u v t u v t u v
t u v u t v tv v u uv v t
u v t tv t v u uv
u v
u v t v t u v t
t u
u v x x x x x
v t
c laø
Khi töùc laø
3 2
2 23 3
7 5 52 3 12 ,
25
6 7 7 8 .3
2
x x x
x
t u x x x x x
- Vậy pt có 6 nghiệm7 5 5 7 5 5 3
; ; 5; .2 2 2
x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 11/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 11 -
Bài 5. Giải bất pt (1)1 1
... 52 4
x x x x x
Giải
ĐK :1
4x ; ta có
2
1 1 1 1
2 4 4 2x x x
.
2
1 1 1 1 1 9(1) ... 5 5
2 4 2 4 4 2
120 20.4
x x x x x x
x x
Bài 6. Giải pt (1)3 36 6 4 4 0x x
- Đặt 3 6 4t x ,
ta có3
3 3 2 2
3
6 4 06( ) 0 ( )( 6) 0
6 4 0
t x t x t x t x t x tx
x t
2 2 6 0
t x
t x tx
, hệ pt trên tương đương với hệ3
2 2
3 3
(I)6 4 0
6 0(II)
6( ) 8 0
t x
t x
t x tx
t x t x
3 2( ) 6 4 0 ( 2)( 2 2) 0
2 1 3 1 3.
2 1 3 1 3
t x t x
I t x t t t
t t t
x x x
2 2
3 3
6 0(II)
6( ) 8 0
t x tx
t x t x
; đặt 2, ( 4 0)S x t P tx S P
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 12/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 12 -
2 2
2
586 0 6 9( )
2( 12) 8 0( 6) 8 0
3
P S P P S II
S S S P S
- Vì 2 4 584 4. 0
9 9S p nên hệ (II) vô nghiệm.
Vậy pt co 3 nghiệm là 2; 1 3.x x
Bài 7. Giải pt 2 32( 3 2) 3 8 (1).x x x
Giải
ĐK : 2.x
- Đặt 22 0; 2 4 0.u x v x x
2 2 2 2(1) 2( ) 3 2 2 3 0 2 ( 2 ) ( 2 ) 0
2( 2 )(2 ) 0
2
u v uv u v uv v v u u v u
v u v u v u
u v
(loaïi)
- 2 22 2 4 2 2 6 4 0 3 13v u x x x x x x
Bài 8. Giải bất pt 21 12 2 18 7
2 4
x x x x
(1).
Giải
ĐK :1
2
x
2 21 1 18 7 1 1 ( 1)(1) 2 1
2 4 8 2 4 8
x x x x x x x x
- Đặt1 1;
2 4
x u x v
, khi đó 2 2 2 22 2 2u v u v u v u v
2 2 2 21 1
2 0 ( ) 0 6 3 02 43 6.
x u uv v u v u v x x x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 13/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 13 -
Vậy nghiệm của bất pt là :1
23 6
x
x
Bài 9. Giải bất pt (1).3 20013 1 2 4 3
304x x x
ĐK : 2x
3 2001(1) 3 1 2 4 3
304x x x ;
xét3
23
2001 1 1 2001( ) 3 1 2 4 ; '( ) 0304 3042 4(3 1)
f x x x x f x x x
Vậy ( ) f x đồng biến, ( ) 3 0 f x x , suy ra tập nghiệm là : 2 0.x
Bài 10. Giải pt (1).2 4 233 1 1
3x x x x
Giải
22 2 2
2
2 2
2 2
3 1(1) 2( 1) ( 1) ( 1)
3 1
1 3 12 1
31 1
x x x x x x x x
x x
x x x x
x x x x
- Đặt (1)
(loaïi)
22
2
1
1 3 3; 0; 2 131 3
2
t x x
t t t t x x
t
- 2 2
2
2 2
1 1 1 1 12 1 1
31 13 3
x x x x t x x x
x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 14/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 14 -
- Vậy pt có một nghiệm 1x .
Bài 11. Giải và biện luận pt (1)3 2 4 4 4x x x x m .
GiảiĐK : 4x
2 2
(1) 4 1 4 2 4 1 4 2x x m x x m
- Đặt (1) (2).4; 0; | 1 | | 2 |t x t t t m
+ TH1 : (2) 30 1; 1 2 2 3 .2m t t t m t m t
Nếu3
0 1 1 32
m m
, thì (2) có nghiệm là
3 34
2 2
m m t x
2
34
2
m x
là nghiệm của (1).
Nếu 1 3m m thì (2) vô nghiệm, do đó (1) cũng vô nghiệm.+ TH2 : 1 2;(2) 1 2 1t t t m m
Nếu 1m thì (2) có vô số nghiệm, do đó (1) cso vô số nghiệm.
Nếu 1m thì (2) vô nghiệm, do đó (1) vô nghiệm.
+ TH3 :3
2;(2) 1 22
m t t t m t
Nếu3
2 12
m m
thì
2
3 3 3(2) 4 4 .
2 2 2
m m m t x x
Nếu 1m thì (2) vô nghiệm, do đó (1) vô nghiệm.
Bài 12. giải pt (1)2 32 4
2
x x x
.
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 15/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 15 -
ĐK : 3x
2 3(1) 2 4 1 1
2
x x x
; đặt
(1)
(2)
2
2
2 4 131;(1)
2 4 12
x y y x y
y x x
[
2 22( ) 4( ) 2( )( ) 5( ) 0
( ) 2( ) 5] 02( ) 5 0
x y y x y x y x y x y x
y x y x y x
y x
Hệ đã cho tương đương với
(I)
(II)
2
2 2
2 4 1
2( ) 5 02( ) 4( ) 2
y x
x y y
y x x y y x y x
- 2
3 17 3 17
4 4( ) .2 3 1 0 3 17 3 17
4 4
x x y x I
y y y y
- 2 22( ) 5 0 2( ) 5 0( )2[( ) 2 ] 3( ) 2 0 2( ) 3( ) 4 2 0
x y x y II x y xy x y x y x y xy
+ Đặt 2; ( 4 0).S x y P xy S P
2
52 5 0
2( )32 3 4 2 0
4
S S II
S S P P
Khi đó ,x y là nghiệm của pt
2 25 3 5 130 4 10 3 0
2 4 4
5 13 5 13
4 4 .5 13 5 13
4 4
X X X X X
x y
y x
Vậy (1) có 4 ngiệm là :5 13 3 17
; .4 4x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 16/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 16 -
Bài 13. Giải pt (1).3
2
1 2
52
x
x
Giải
ĐK : 1x ; đặt 21; 1 .u x v x x
2 2
2 2
2(1) 2( ) 5 2 ( 2 ) ( 2 ) 0
52
( 2 )(2 ) 02
uv u v uv u u v v u v
u v
u v u v u v
v u
-
2 2 2
2 1 2 1 1 4( 1) 4 5 3 0( )u v x x x x x x x x VN
- 2 2 2 5 372 2 1 1 4 4 1 5 3 0
2v u x x x x x x x x x
Vậy (1) có 2 nghiệm5 37
2x
.
Bài 14. Giải pt (1).3 32 23 7 1 8 8 1 2x x x x x
Giải
- Đặt 3 32 23 7 1; 8; 8 1 2,u x v x x w x x u v w
- Ta có, 3 3u v w u v w
Suy ra, 3 3 3 3 )(u v w u v w u v v w u w
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 17/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 17 -
3 23
3 32 2
3 23
2
2 2
2
7 1 8
)( 8 8 1
7 1 8 1
7 1 8
8 8 1
7 1 8 1
x x x u v
u v v w u w v w x x x x
u w x x x
x x x x x x x
x x x x x x
x x x x x x x
- Vậy pt có 4 nghiệm 0; 1; 9.x x x
Phương trình và bất pt mũ, lôgarit
Bài 1. Giải pt (1).2
2 7 7log log ( 3) log 2 log ( 3)
2x x x x x x
Giải
ĐK : 0x
[ ]=0
2
2 2 7 2
22 2 7
2 7
(1) log log 2 log ( 3) log 02 2
loglog log 2 log ( 3) 22 log 2 log ( 3)
x x x x x
x x x x x x
x x
- 2 2
2
ln ln 2log 2 ln( ) ln 2
2 2x x x x
x x x x
Xét2
ln 1 ln( ) ; 0 '( ) ; '( ) 0 0
t t f t t f t f t t
t t
, suy ra pt có nhiều nhất là hai
nghiệm, 2; 4x x (nhẩm nghiệm)
- 2 7
log 2 log ( 3)x x , đặt2
log 2t t x x
Ta có, 2 2 2
7log ( 3) ( 3) 7 (2 3) 7 4 6.2 9 7t t t t t t
x t x
4 2 96 1
7 7 7
t t
t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 18/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 18 -
+ Xét4 2 9 4 4 2 2 9 1
( ) 6 '( ) ln 6 ln ln 0 ( ) .7 7 7 7 7 7 77 7
t t t t
t t f t f t f t N B
Suy ra, ( ) 1 f t có duy nhất một nghiệm là2
2 log 2 4t x x
KL : (1) có hai nghiệm là 2; 4x x .
Bài 2. CMR không tồn tại a để bất pt sau có nghiệm duy nhất :
1
2
log 11 log 2 3 log 2a a
ax x ax x
Giải
ĐK :ax x
a
; đặt ; .t ax x t
log loglog 11 log log 11 log
log log
log loglog 11 . log log 11 . log *
log log
a a
a a a a
a a
a a
a a a a
a a
t t t t
t t t t
- Nếu 1 log 2 0a
a thì (*) log 2. log 11 log . loga a a a
t t
+ Xét ( ) log . loga a
f t t t
(2
2
1'( ) . log ( 1) . log 1 1; 0)
( 1) ln( 2) ln a a
t f t t t a t
t a t a
Do đó, ( ); 0 f t t là hàm đồng biến, ( ) 3 3 f t t , BPT có vô số nghiệm
- Nếu (*)20 1 log 2 0, log 2. log 11 log 2 log ( 1)
a a a a a a t t
Tương tự trường hợp trên ta có, ( ) (3) 3 f t f t hay 2 22 1 9 2 8 0ax x ax x ,
vì bất phương trình này luôn có nhiều hơn một nghiệm nên không tồn tại a để BPT có nghiệm duynhất.
Bài 3. Giải PT2 2
1 1 12 2
x
a a a a
, với 0 1a
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 19/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 19 -
Giải
Chia hai vế của pt cho21
2
x
a
a
ta được, (*)
2
2 2
1 21
1 1
x
a a
a a
- Đặt tan ;04
a t t
, ta có, os(*) (sin2 ) ( 2 ) 1x x t c t
Vì os0 sin 2 1, 0 2 1t c t nên os(sin 2 ) ( 2 )x x t c t là hàm nghịch biến, do đó PT có nghiệm
duy nhất 2.x
2. Phương trình và bất phương trình lượng giác
Bài 1. Giải pt 1 cos cos cos cos16
x x x x
Giải
2 2
1 3 1 3 1cos cos cos cos
4 4 4 4 2
cos
cos cos
cos
cos cos
cos
cos cos
PT x x x x
x
x x
x
x x
x
x x
- (loaïi)cos
cos
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 20/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 20 -
-
1cos
3 12cos cos1 2 2(2) cos
1 2 1 3
cos3 32 2 2cos2 2
x
x x x
x x
5cos cos
62
cos cos3
cos cos3
cos cos6
x
x
x
x
2 52 | | 2
3 6 ( )
2 | | 26 3
k x k k
k x k
-
3cos cos cos cos 2
2 6 6(3) ( )5 53cos cos cos 2cos6 62
x x x x k k
x x x k x
Vậy bất pt đã cho có nghiệm là
2 5
2 | | 23 6 ( ).
2 | | 23 6
k x k k
k x k
Bài 2. Giải pt 3 1 tan sin cos sin cosx x x x x
ĐK :
cos .sintan
cos
k x k x x x
k x k x x k
x k
k x k
k x k
3 1 tan tan tanx x x ; đặt tant x , ta được :
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 21/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 21 -
(*)3 1 ( 2) 5( 3)t t t
- Đặt 21 1u t t u
2 2 3 2 2(*) 3 ( 1) 5( 2) 3 5 3 10 0 ( 2)(3 5) 0
2 1 2 3 tan arctan .
u u u u u u u u u
u t t x x k
- Vậy pt đã cho có nghiệm là arctan .x k k
Bài tập
Bài 1. Giải pt tansin cos3 1 tan
sin cosx x x
x x x
Giải
ĐK :
cos .sintan
cos
sin cos tanarctan
x x k x k x
x x k k x k
x x x x k
tantan1 tan
tanx x
x x
, đặt tant x , ta được,
*3 1 t t t
t
- Ta xét hàm số212
( ) 1 ; ( ) ; ( ) 23
t t f t t g t h t
t
- Vì ( ), ( ) f t g t là các hàm đồng biến nên ( ). ( ) f t g t cũng là hàm đồng biến, mặt khác ( )h t là
hàm nghịch biến nên (*) có nghiệm duy nhất, ta nhẩm được nghiệm đó là 0t
- Suy ra, tanx x k k .
Bài 2. Giải BPT | cos | | cos | | cos | | cos |x x x x
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 22/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 22 -
- Giả sử | cos |x
Đặt | cos | cos cos | cos | | cos | | |x x x x t x t t
(1)2| cos | | cos | 1 2 (1 2 ) 1 1x x t t t t
+ TH1: | cos |x
Chứng minh tương tự trên ta có, (2)1
| cos | | cos |x x
Từ (1) và (2) ta có: 3| cos | | cos | | cos | | cos | 22
x x x x
+ TH2:1
| cos |2
x
Vì | cos | | cos | | cos | | cos | | cos |x x x x x
| cos | | cos | | cos | | cos |x x x x
- Giả sử1
| cos |x
+ TH1:1
| cos |2
x , chứng minh tương tự trên ta có | cos | | cos | 1x x
Suy ra, | cos | | cos | | cos | | cos | | cos | | cos | | cos |x x x x x x x
+ TH2:1
| cos |x
Khi1
| cos | | cos | | cos | 12
x x x , ta có điều phải chứng minh
Khi
1
| cos | 2x , ta luôn có điều phải chứng minh.
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 23/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 23 -
Bài 6. Cho ( ),n P x n thỏa2
0 1
( )( ) 0, ( ) ( ) ; 1
2n
n n
x P x P x P x P x n
. CMR:
20 ( )
1n x P xn
Giải
+ Với 0n thì2
01 0 0
( )( ) ( ) 0 ( )
2 2 x P x x
P x P x P x
+ Với 1n thì2
12 1 1
( )( ) ( ) ( )
2 2 4 2 x P x x x x
P x P x P x
+ …Vậy 10 ( ) ( )n n P x P x
Mặt khác
22
1 1
1 ( )( )1 ( ) 1 ( ) 0 ( ) 1
2 2 2nn
n n n
P x x P x x P x P x P x
Vậy ( ),n P x n tăng và bị chặn
+ Đặt lim ( ) ( )nn
P x f x
. Từ công thức đã cho ta được 2( ) ( ) x x f x x
Do ( ),n P x n tăng nên ( ) ( )n P x f x x
Đặt
2
1 1
( )( ) ( ) ( ) ( ) ( )
2
( )( ( )) ( )
( ) ( ) 1 ( ) 12 2 2
nn n n n n
n n n
n n n
x P xu x x P x u x x P x u x
u x x P x x P x x
u x u x u x
2
1 2( ) ( ) 1 ( ) 1 ... 12 2 2
n
n n n
x xu x u x u x x
Xét hàm số 12
nt
y t
trong đó ; 0;1t x t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 24/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 24 -
1
0;1
2' 1 . . 1 ; ' 0
2 2 2 1
2max
1
n n
t
t n t y t y x
n
y
n
Mặt khác 12
nt
y t
trong đó 0;1t nên 0 y
Suy ra2
0 ( )1n x P x
n
Bài 7 Giải hệ
2 2 2 32
34
1
8
x y z
xy yz zx
xyz
(1)
Giải
2 3( ) 2( )
23
(1)4
1
8
0 3
41
8
x y z xy yz zx
xy yz zx
xyz
x y z xy yz zx
xyz
Theo định lí viet ta có , , x y z là nghiệm của pt
3 33 1 10 4 3 0
4 8 2t t t t (2)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 25/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 25 -
Đặt cos ;(0 ) t u u
3 1(2) 4cos 3cos 0
2
1cos32
5 7; ;
9 9 9
u u
u
u uu u u
Vậy5 7
cos ; ;9 9 9
x y z
và các hoán vị của chúng
Bài 8 Tìm m để hệ
3
3
0
0
(1)
(2)
x mx y
y my x
có 5 nghiệm
Giải
+ 0 x y là một nghiệm của hệ
+ Ta tìm m để hệ có 4 nghiệm khác 0
Hệ
4 24 4 2 2
4 2
0
( ) 00
x mx yx
x y m x y m y my yx
Thế 3 x mx vào (2) ta được
3 3 3
2 2 3 2
( ) ( ) 0
( ) ( ) 1 0
x mx m x mx x
x x m m x m
Đặt 2 ,t x m t m
Phương trình trở thành
2 3 4 3
22
2
( ) 1 0 1 0
1 10 ( 0)
1 12 0
t m t mt t mt mt
t mt m t t t
t m t t t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 26/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 26 -
Đặt1
u t t
. Phương trình trở thành 2 2 0 (3) u mu
+ Pt có 2 nghiệm 2 8 0 2 2m m
+ Ta có 211 0u t t ut
t : có 2 nghiệm trái dấu thỏa mãn 1 20m t t
Suy ra ứng với mỗi t thì pt 2 t m có 2 nghiệm x
Vậy 2 2m là giá trị cần tìm
Bài 9 Giải hệ2 2 4 4 6 2
2 3 3
2 (1 )
1 ( ) (3 ) 0
y x y y x x
x y x y x
Giải
Hệ
2 2 2 6 2
2 3 3
1 (1 ) (1 )
1 ( ) (2 )
(1)
(2)
x y y x x
x y x y x
Lấy (1) – (2) ta được
2 2 2 2 6 2 3 3 3
2 2 2 2 6 2 3
2 2 2 2 3 2
1 (1 ) 1 ( ) 2
1 (1 ) 1 ( ) 2
1 (1 ) 1 ( ) ( )
y x y y x x xy x
x y x y y x xy
x y x y x y
Ta thấy 0; 0 0VP VT VT VP
2 2 2 2 3 21 (1 ) 1 ( ) ( ) 0 x y x y x y
33
2 2 2 22 2
1
1
11 (1 ) 1 ( )1
1
x x y
x y y x y
x x y x y x y
y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 27/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 27 -
Thử lại thấy (1; -1) là nghiệm của hệ
Bài 10 Cho 17a b c . CMR hệ
2 1
0 1
ax bx c
x
có nghiệm
Giải
Giả sử hệ vô nghiệm thì 2 1; 0,1ax bx c x
Cho
1 11
12 4 2
0 1
x a b ca b
x c
x c
Xét hệ
2 4 2
3 44 2
C a b ca A B C
a b B c b A B C
c A A c
Khi đó
2 4 2 3 4
2 4 2 3 4 17
a b c A B C A B C A
A B C A B C A
Mâu thuẫn với giả thiết. Vậy hệ có nghiệm
Bài 11. Giải và biện luân hệ
2 2
2 2
2 2
(1)
(2)
(3)
x m y m k
y n z n k
z p x p k
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 28/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 28 -
Với3
, , 02
k m n p m n p
Giải
+ Giả sử ( ; ; ),( '; '; ') x y z x y z là 2 nghiệm phân biệt của hệ và ' x x
Từ (1): 2 2 2 2' ' ' x m y m k x m y m y y
Từ (2): 2 2 2 2' ' ' y n z n k y n z n z z
Từ (3): 2 2 2 2' ' ' p x p k z p x p x x
Do đó hệ đã cho nếu có nghiệm thì có nghiệm duy nhất
+ Ta chỉ cần chỉ ra 1 nghiệm của hệ
Xét tam giác đều ABC cạnh k: Từ một điểm bất kì trong tam giác thì khoảng cách từ điểm đó đềncác cạnh có tổng bằng đường cao. Nên ta tìm được điểm I sao cho
32
IM m
IN n
IP pk
IM IN IP
Khi đó
2 2 22 2
2 2 2
MA IA IM x m x m y m k
MB IB IM y m
( thỏa (1) )
Tương tự các trương hợp còn lại.
A
B C
I
N
PM
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 29/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 29 -
Bài 12 Giải hệ phương trình
x x y
y z
z x z
e y e
e z e
e x e
Giải
+ Nếu 0 ta có hệ1 (1)
(2)
y
y y z
y e
e z e
Đặt ( ) 1 f y y e
'( ) 1 0, y f y e y : hàm số nghịch biến
'(0) 0 Do đó ( ) 0 f y có nghiệm duy nhất 0 0 y z
Hệ có nghiệm 0 x y z
+ Nếu 0 0 yz . Khi đó hệ tương đương với
1 .1
11 .1
1
.11
1
( )
y x x
y y
z y y
z z
x z z
x x
y ee y ee
e y ee z e
e e
y eee x
ee
Xét hàm2
. ( 1)( ) '( ) 0, ( )
1 ( 1)
t t t
t t
t e e e t t g t t g t
e e
đồng biến
Khi đó : nếu
( ) ( )
( ) ( )
(voâ lí)
z x
y z
y g x g y e e
z x g z g x
e e y z x
Do đó 0 x hệ vô nghiệm. Vậy nghiệm của hệ là 0 x y z
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 30/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 30 -
Bài 13. Giải hệ phương trình3 2 3 21 1
6 4 2
0 , 1
ln
64 96 36 3 0
(1)
(2)
x x x y y y
x y
xe e
y
x y x
Giải
+ PT (1)3 2 3 21 1ln ln x x x y y ye x e y
Xét hàm số
3 2
3 2
1
2 1
( ) ln ; 0 1
1'( ) (3 2 1) 0; 0 1
t t t
t t t
f t e t t
t t t e t t
( ) f t là hàm số đồng biến. Mà ( ) ( ) x f y x y
+ Thay x y vào (2) ta được: 6 4 264 96 36 3 0 x x
Đặt cos 0;2
; x u u
. PT trở thành: 6 4 246cos 96cos 36cos 3 0u u u
3 2 4 2
23
2
4 (4cos ) 24cos 9cos 3 0
4 4cos 3cos 2 1
2 2cos 3 1 1
1cos6
2
18 3
u u u
u u
u
u
k
u
Do5 7
0; ; ;2 18 18 18
u u u u
Vậy hệ đã cho có 3 nghiệm là5 5 7 7
cos ;cos ; cos ;cos ; cos ;cos18 18 18 18 18 18
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 31/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 31 -
Bài 14 Giải hệ
3 2
3 2
2 2
(13 ) (2 2 2 26) 5 7 7 30 0
(17 ) (2 2 2 26) 3 2 0
11 28 0
(1)
(2)
x x y z x y z yz yz y z
x x y z x y z yz yz y z
x x
(3)
Giải
+ Từ (3) ta có : 4 7 (*)
+ Đặtu y z
v yz
thì (1) và (2) trở thành
3 2
3 2
2 3 2
2 2
(13 ) (2 2 26) 5 7 30 0
(17 ) (2 2 26) 3 2 0
(2 7) (5 ) 13 26 30 0
(1 2 ) ( 2 3) 17 26 2 0
5 5
5 1 5 1
x x u x u v v u
x x u x u v v u
u x x v x x x x
u x x v x x x
u x y z x
v x yz x
Suy ra y, z là nghiệm của pt : 2 ( 5) 5 1 0 X x X x
PT có nghiệm 2 310 21 0 7
7(do (*))
x x x x
x
Thay x = 7 vào pt ta được y = z = 6
Vậy nghiệm của hệ là (7;6;6)
Bài 15 Cho hệ
2
2
2
0;
ax bx c y
ay by c z a
az bz c x
. CMR: 2
1 4 0b ac thì hệ vô nghiệm
Giải:
Cộng 3 phương trình ta được
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 32/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 32 -
2 2 2( 1) ( 1) ( 1) 0ax b x c ay b y c az b z c (*)
Đặt 2( ) ( 1) f t at b t c . Khi đó (*) trở thành: ( ) ( ) ( ) 0 f x f y f z
Từ giả thiết2( 1) 4 0 ( ) 0
( ) 0;
( ) ( ) ( ) 0; , ,
( ( ) ( ) ( )) 0; , ,
voâ nghieämb ac f t
af t t
af x af y af z x y z
a f x f y f z x y z
Suy ra (*) vô nghiệm hay hệ đã cho vô nghiệm
Bài 16 Tìm a sao cho:2 2
2 2
12 7
1
3 10 5 2
(1)
(2)
a x xy y
a
x xy y
có nghiệm
Giải
+ Lấy (1) nhân 2 trừ cho (2) ta được : 2 4( 3 ) 1
1 x y a
a
+ Khi đó, lấy a bất kì: a < -1 thì1
11
a
a
. Lúc đó ta xét hệ
2 2
2 2
2 7 1
3 10 5 2
(3)
(4)
x xy y
x xy y
Lấy 2 nhân (3) trừ (4) ta được: 2( 3 ) 0 3 x y x y
Thay x = - 3y vào (3) ta được pt: 2 2 19 6 7 1
2 y y y y
Với a < -1 thay
3 3
2 21 1
2 2
x x
y y
vào hệ đã cho (thỏa)
Vậy a < -1 là giá trị cần tìm
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 33/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 33 -
Bài 17. Giải hệ2 2 2 2
3 3 3 3
tan tan tan
tan tan tan
x y z m
x y z m
Giải
ĐK
2
2
2
k
k
k
Đặt tan ; tan ; tanu x v y w z
Ta quy về hệ sau:2 2 2 2
3 3 3 3
u v w m
u v w m
+ Nếu m = 0 thì
2 2 2 0 0 tan tan tan 0
u v w u v w u v w
x k
y l
z p
+ Nếu 0m thì
6 2 2 2 2 2 2 4 4 4
2 4 4 4
4 4 4 4
( . . . ) ( )( )
( )=
m u u v v w w u v w u v w
m u v w
u v w m
Mặt khác ta có
4 2 2 2 2 4 4 4 2 2 2 2 2 2
4 2 2 2 2 2 2
( ) 2( )
2( )
m u v w u v w u v u w v w
m u v u w v w
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 34/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 34 -
2 2 2 2 2 2
0
0 0 0
0
u v
u v u w v w uv uw vw v w
w u
TH1:tan tan 0
0tan
arctan
x k x y
u v w m y l z m
m p
TH2:tan tan 0
0tan
arctan
z k z y
w v u m y l x m
x m p
TH3:tan tan 0
0tan
arctan
x k x z
u w v m z l y m
m p
Vậy hệ có nghiệm
k
l
p
;
arctan
x k
z l
y m p
và các hoán vị
Bài 18 Giải hệ3 2 2
2 2
(2 )(3 2 ) 3
3 3 2
6
3
(1)
(2)
(3)
(4)
x x z z
y y x x
y z z
z
Giải
Từ (3) 2 26 0 0 6 y z z z
Từ (1) 23 2(3 ) 3 3 0 x z x z . Phương trình nay có nghiệm khi
2 03 0
3
z z z
z
Khi đó ta có:
30
0 6
30 3
z z
z
z z z
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 35/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 35 -
+ Với1
00
x z
y
+ Với
23 3
x z y
Vậy hệ có nghiệm là (1;0;0); (2;-3;3)
Bài 19 Giải hệ ; , , 0
(1)
(2)
(3)
a bc xz
x zb c
a xy a b c y x
c ab yz
z y
Giải
Lấy (1).c + (2).a +(3).b ta được:
2 2 2
2 2 2
( ) ( ) ( )
0
(*)
ac bc ab ac bc abb yz a xy c xz x z y y z z
a b c axy byz czy
a b c axy byz czy
Quy đông pt trong hệ ta được
2 2
2 2
2 2
az bx cxz x z
bx cy axy x y
cy az byz y z
Cộng các pt ta được
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
0
(**)
az bx bx cy cy az axy byz cxz y z x y x z
axy byz cxz y z x y x z
axy byz cxz y z x y x z
Lấy (*) + (**) ta được
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 36/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 36 -
2 2 2( ) ( ) ( ) 0
yx a
a xy b yz c xz yz b
x c
Nhân các pt trong hệ ta suy ra 2 2 2 y z abc xyz abc
Từ đó ta có nghiệm của hệ là
ac ac x x
b b
ab ab y y
c c
bc bc z z
a a
( Vì x,y,z cùng dấu)
Bài 20 Giải hệ
2
2
2
2
2
2
x x y y
y z z
z x x
GiảiTa thấy x = y =z =0 là một nghiệm của hệ
Mặt khác 1; 1; 1 y z không phải là nghiệm của hệ
Khi đó ta đưa hệ về dạng:
2
2
2
2
12
1 2
1
y x y
z
x z
Đặt
2
2tantan tan 2 tan 4 tan8
1 tan
tan tan87
a x a y a z a x a
ak
x a a a
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 37/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 37 -
Thử lại (thỏa)
Vậy hệ có nghiệm (0;0;0);2 4
tan ;tan ;tan7 7 7
k k k
PHẦN II : BẤT ĐẲNG THỨC
I. BẤT ĐẲNG THỨC CƠ BẢN
Bài 1: Cho A, B, C là 3 góc của một tam giác bất kì. Tìm GTLN của biểu thức:
4cos 4cos 3cos F A B C
Khái quát: Cho 0 2M N . Tìm GTLN của cos cos cos F M A M B N C
Giải
Vì A, B, C là 3 góc của một tam giác nên ta có
cos sin2 2 2 2 2 B C A B C
2 2
22
4cos 4cos 3cos 4(cos cos ) 3cos
8cos cos 3 1 sin 6sin 8sin cos 32 2 2 2 2 2
2 8 8 176 sin cos cos 3 3
2 3 2 3 2 3 3
F A B C A B C
A B A B C C C A B
C A B A B
Dấu = xảy ra khi
2cos 122
sin cos2 3 2
A B
C A B
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 38/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 38 -
cos 1 22 2
2 2sin cos sin
2 3 2 2 3cos 1 2
2 22 2
sin cos sin2 3 2 2 3
(loaïi)
A B A Bk
C A B C
A B A Bk
C A B C
0( 0 0)
2 22arcsin 2arcsin
3 3
vì A B k A B C A B
C C
Vậy GTLN của F là17
3
Khái quát tương tự trên, ta có
2
2 2 2
2
cos cos cos 2 sin 2 sin cos2 2 2
2 sin cos cos2 2 2 2 2 2
C C A B F M A M B N C N M N
C M A B M A B M N N N N N N
Vậy GTLN của F là2
2
M N
N . Đạt được khi
2arcsin2
A B
M C
Bài 2 Cho
2 2 2 2 2 2
0 p q a b c d . Cmr 2 2 2 2 2 2 2( )( ) ( )a c q b d pq ab cd
Tổng quát cho nhiều cặp số
Cho 2 2 2 2
1 1
0n n
k k k k
p q a b
. Cmr
2
2 2 2 2
1 1 1
n n n
k k k k k k k
a q b pq a b
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 39/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 39 -
+ Nếu 2 2 2 2 2 2( )( ) 0 p a c q b d thì (1) đúng
+ Nếu 2 2 2 2 2 2( )( ) 0 p a c q b d thì kết hợp với đk bài toán ta có
2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2( )( ) 0 0 0
0 0 p a c q b d p a c pq
p q a b c d q b d
Xét tam thức bậc hai
2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2
2 2 2
( ) ( ) 2( )
2 2 2
( ) ( ) ( )
f x p a c x pq ab cd x q b d
p x pqx q a x abx b c x cdx d
px q ax b cx d
2 2 2( ) 0 p
p a c f q
( ) 0 f x có nghiệm
2 2 2 2 2 2 2( ) ( )( ) 0
ñpcm
pq ab cd p a c q b d
Khái quát tương tự ta xét 2 2
1
( ) ( ) ( )n
k k k
f x px q a x b
có nghiệm suy ra kết luận
Bài 3 Cho a b c . Cmr 2 2 23 3a a b c a b c ab bc ca c
Giải
Xét tam thức 2( ) 3 2( ) x x a b c x ab bc ca có nghiệm
2 2 2
1,2 3a b c a b c ab bc ca
x
Mà ta lại có
2
2
3 ( ) 3 2( )
( ) ( )
( )( ) 0
3 ( ) ( )( ) 0
(gt)
(gt)
f a a a b c a ab bc ca
a ab ac bc a a b c a b
a b a c
f c c b c a
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 40/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 40 -
Và3
a b ca c
2 2 2
1,2 3 ñpcm
a b c a b c ab bc ca
a x c a c
II. Bất đẳng thức Cauchy
Bài 1. Tìm nghiệm dương của hệ2 2 2
32
4 4 2 96
xyz
x xy y z
GiảiÁp dụng BĐT Cauchy ta có
2 2 2 2 2 2 2
23
4 4 2 ( ) ( 4 ) 4
2 4 4 2( 2 2 )
2.3 4( ) 96 1
(do )
x xy y z x z z y xy
xz yz xy xz yz xy
xyz xyz
Dấu bằng xảy ra khi
2 2 24
2 22 232 4, , 0
32
x z y
x z y y xz yz xy xyz x z x y z
xyz
Vậy2
4
y
x z
là nghiệm của hệ
Bất đẳng thức ( ) ( ) ( ) ( ) ( ) ( ) F A F B F C G A G B G C
Bài 1. Cmr x , ta có
12 15 203 4 5
5 4 3
x x x x x x
Khi nào dấu đẳng thức xảy ra
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 41/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 41 -
a) Cho , , 0a b c . Cmr 2 2 2a b c a bc b ca c ab
b) Cho , , 0 x y z thỏa mãn 1 xyz . Cmr 2 2 2 3
1 1 1 2 x y z
y z x
Giải
Áp dụng BĐT Cauchy ta có
2
2
2
12 152 (3 ) 2.3
5 4
12 202 (4 ) 2.4
5 3
15 202 (5 ) 2.54 3
x x x x
x x x x
x x x x
12 15 202 2(3 4 5 )
5 4 3
x x x x x x
đpcm
Dấu = xảy ra khi
12 15
5 4 015 20
4 3
x x
x xx
a) Áp dụng BĐT Cauchy ta có
2 2 2 2 2 2( ) ( ) ( ) 2 2 2 ( ) ( ) ( )
2 2 2
a b b c c a ab bc ca ab bc bc ca ca ab
a bc b ca c ab
đpcm
Dấu = xảy ra khi2 2 2a b c
a b cab bc ca
b) Áp dụng BĐT Cauchy ta có
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 42/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 42 -
2
2 2 2 2
2
11 4
1 13
1 4 1 1 1 41
1 4
x y x
y
y z x y z y x y z x y z
z y z x z x
z x
2 2 2
33 3 3
1 3 11 1 1 4 4 2 x y z
x y z xyz y z x
Dấu = xảy ra khi 1
1
x y z x y z
xyz
Bài 2 Cho các số dương , , y z thỏa mãn 1 xyz . Cmr:
3 3 3 3 3 31 1 13 3
x y y z z x
xy yz zx
GiảiÁp dụng BĐT Cauchy ta có
33 3 3
33 3 3
33 3 3
1 3 3
1 3 3
1 3 3
y xy xy
z yz yz
x zx zx
3 3 3 3 3 33 3 3 3 3 3
23
1 1 11 1 1
3 3 3 3( ) 3.3 3 3
x y y z z x x y x z x y z x
xy yz zx
z xy x yz y zx z xy x yz y zx xyz
Vậy3 3 3 3 3 31 1 1
3 3 x y y z z x
xy yz zx
Dấu = xảy ra khi 1 x y z
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 43/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 43 -
Bài 3. Cho , , 0 y x thỏa mãn 1 xyz . Cmr :
1 1 112 2 2 x y z x y z x y z
a)1 1 1 9 1 1 1 1 1
9a b c a b c a b c a b c
b)1 1 4 1 1 1 1
4a b a b a b a b
Giải
+ Trước tiên ta cm với , 0a b thì1 1 1 1
4a b a b
Thật vậy, áp dung BĐT Cauchy ta có
2
1 1 1 1 1 141 1 1 42
a b aba b
a b a b a ba b ab
+ Áp dụng BĐT trên ta có
1 1 1 1 12 ( ) ( ) 4
1 1 1 1 1
2 ( ) ( ) 4
1 1 1 1 1
2 ( ) ( ) 4
y z x y x z x y x z
y z x y y z x y y z
y z x z y z x z z z
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 44/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 44 -
1 1 1 1 1 1 1
2 2 2 2
1 1 1 1 1 1 1 1 1 1 1 1 1 11
2 4 4 4 4
x y z x y z x y z x y y z z x
x y y z z x x y z
Dấu = xảy ra khi3
1 1 14 4
, , 0
x y y z z x
x y z
x y z
x y z
x y z
LUYỆN TẬP
Bài 1. Cho 2 3, , 0 1 x y z xy z . Cmr: 2 3 6 x y z
Giải
Ta có
2 362 3 6 6 x y z x y y z z z xy z
Dấu = xảy ra khi 2 3 1 1
, , 0
x y z
xy z x y z
x y z
Bài 2. Cho1 1 1
, , 0 1 x y z x y z
. Cmr: 9 x y z
Giải
Áp dung BĐT Cauchy ta có
3
3
31 1 1
9 91 1 1 13
x y z xyz
x y z x y z x y z
x y z xyz
Dấu = xảy ra khi 31 1 1 1
x y z
x y z x y z
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 45/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 45 -
Bài 3. Cho , , , , 0a b c a b c . Cmr
a)2 2 2
2 2 2
a b c a b c
b c a b c a b)
3 3 3
3 3 3
a b c a b c
b c a b c a
c)2 2 2
2 2 2
a b c b c a
b c a a b c
Giải
a) Áp dụng BĐT Cauchy ta có
2
2
2 2 2 2
2 2 2 2
2
2
1 2 2
1 2 2 3 2
1 2 2
a a a
b b b
b b b a b c a b c
c c c b c a b c a
c c c
a a a
(1)
Mặt khác ta có
2 2 2
32 2 2 3 . . 3
a b c a b c
b c a b c a (2)
Từ (1) và (2) ta suy ra
2 2 2 2 2 2
2 2 2 2 2 22 2
a b c a b c a b c a b c
b c a b c a b c a b c a
b) Do , , 0a b c nên áp dụng BĐT Cauchy ta có
3 3
33 3
3 3 3 3 3
33 3 3 3 3
3 3
33 3
1 1 3 3.
1 1 3 3. 6 3
1 1 3 3.
a a a
b b b
b b b a b c a b c
c c c b c a b c a
c c ca a a
(3)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 46/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 46 -
Mặt khác ta có
3 3 3 3 3 3
33 3 3 3 3 36 2.3 . . 2
a b c a b c
b c a b c a
(4)
Từ (3) và (4) ta suy ra đpcm
c) Áp dụng BĐT Cauchy ta có
2 2 2 2
2 2 2 2
2 2 2 2
2 2 2 2
2 2 2 2
2 2 2 2
2 . 2 2.
2 . 2 2.
2 . 2 2.
a b a b a a
b c b c c c
a c a c c cb b b b a a
c b c b c c
a c a c a a
đpcm
Bài 4: Cho x,y thay đổi. Tìm GTNN của
2 2 2 2( 1) ( 1) 2 A x y x y y
Giải
Trong mp Oxy, xét ( 1; )M x y và ( 1; ) x y
Theo BĐT tam giác ta có OM ON MN nên:
2 2 2 2 2 2( 1) ( 1) 4 4 2 1 x y x y y y
Do đó 22 1 2 : ( ) y y f y
+ Với 2 y ta có 2( ) 2 1 2 f y y y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 47/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 47 -
2
2
2
2 2
2'( ) 1
1
2'( ) 0 1 0 2 1
10
4 1
1
3
y f y
y
y f y y y
y y
y
y
Ta có bảng biến thiên
y 13
2
'( ) f y 0
( ) f y
2 5
2 3
( ) 2 3Min f y
+ Với 2 y ta có 2( ) 2 1 2 5 2 3 f y y
Vậy 2 3 A . Đạt được khi 01
3
x y
Bài 5: Cho , , 0 x y z , và 0 xyz . Tìm
2 2 2( ) ( ) ( )min
2 2 2
x y z y z x z x y
y y z z z z x x x x y y
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 48/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 48 -
Ta có
22 2 2 2
2 2( ) 2
.
yz y z y z x x
y z y z y y z z
Với 2 2 2 1 yz x y z x x y yz z
Tương tự ta cũng có:2
2
( ) 2
( ) 2
y z x y y
x y z z
Đặt , , a x x b y y c z z . Ta được
2 2 2( ) ( ) ( )
2 2 22 2 2
x y z y z x z x y a b c
b c c a a b y y z z z z x x x x y y
Khi đó bài toán chuyển thành:
Cho , , 0a b c và 1abc . Tìm min2 2 2
a b c
b c c a a b
Ta có
2
2. ( 2 ) . ( 2 ) . ( 2 )
2 2 2
a b ca b c a b c b c a c a b
b c c a a b
Áp dụng BĐT Bunhiacopski ta có
2
3 3 32 2 2
a b ca b c ab bc ca
b c c a a b
2
2 2 2 3 3 3
a b ca b c
b c c a a b ab bc ca
Mà
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 49/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 49 -
2 2 2 2 2 2
2
2 2 2 3
3
a b c ab bc ca a b c ab bc ca ab bc ca
a b c ab bc ca
Do đó ta được
12 2 2
a b c
b c c a a b
min 12 2 2
a b c
b c c a a b
. Đạt được khi 11
a b ca b c
abc
Bài 6: Cho , , 0 x y z . Tìm
1 1 1min
2 2 2
x y z x y z
yz zx xy
Giải
Ta có
1 1 12
2 2 2 2 2 2
1 12 2 2
x y z x y z x y z xyz
yz zx xy yz zx xy
x y z xyz
z zx xy
Áp dụng BĐT Cauchy ta có
3
3
1 1 39
1 11 2 2 2 232 2 2 8
xyz xyz x y z
xyz x y z yz zx xy yz zx xy xyz
Vậy1 1 1 9
min
2 2 2 2
x y z x y z
yz zx xy
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 50/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 50 -
Đạt được khi 1 x y z
Bài 7: Cho , , x y z là 3 số dương và 1 y z . Chứng minh rằng
2 2 22 2 2
1 1 182 x y z
x y z
Giải
Với mọi , ,u v w
ta luôn có
u v w u v w
Xét1 1 1
; , ; , ;u x v y w z x y z
. Ta có
2
2 2 2 2
2 2 2
23
23
1 1 1 1 1 1
: ( )
1 99 9 9
P x y z x y z x y z x y z
xyz t t xyz
Với 23t xyz . Đk:
21
03 9
x y zt
Đặt9
( ) 9 f t t t
,1
0;9
t
2
9 1'( ) 9 0, (0; ]
9 f t t
t
hàm số nghịch biến. Do đó1
( ) 829
f t f
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 51/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 51 -
Vậy 82 P . Đạt được khi 23
1 1
9 3, , 0
x y z
xyz x y z
x y z
Bài 8: Chứng minh
2 2 22 2 2 3 2
: 1 1 12
A x y y z z z
Giải
Với mọi ,u v ta có
u v u v
Đặt ;1 , 1 ; , ;1 , ' 1 ;u x y v z y w z x w x z
. Ta có
+ 2 2 22 21 1 1 1u v u v x y y z x z
+ 2 2 2 2 2(1 ) (1 ) 1 (1 )v w v w y z z x x y
+ 2 2 2 2 2' ' (1 ) (1 ) 1 (1 )v w v w v w x y z x y z
2 2 22 1 (1 ) 1 (1 ) 1 (1 )u v w z x x y y z
Đặt (1;1 ); (1;1 ); (1;1 )a z x b x y c y z
2 2 21 (1 ) 1 (1 ) 1 (1 ) 18 3 2a b c a b c z x x y y z
3 22 3 2
2u v w u v w
đpcm
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 52/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 52 -
Bài 9. Cho 0a b . Cmr:1 1
2 22 2
b aa b
a b
Giải
2 2
2 2
2 2
2 22 2
22
1 1 1 12 2 log 2 log 2
2 2 2 2
1 1 1 1log 2 log 2
2 2
1 1log 2 log 2
2 2
1 1log 2 1 log 2 12 2
1log 1
2
a b
a b
a
b aa b a b
a b a b
a ba b
a ba b
a b
a b
a
b a
a b
22
2 2
1log 1
2
1 1ln 1 ln 1
2 2ln 2 ln 2
bb
a b
a b
Đặt 2 2 1 1; (do )a b x y x y a b
Xét hàm số:2
1ln 1
( )ln
t f t t
YCBT tương đương với bài toán: Cho 1 x y . Cmr ( ) ( ) x f y
Ta có
23 2 222
2 2
2 12 1 1 1 .ln ln 1. .ln .ln 1 11 11 1'( ) . 0 1
ln ln,
t t t t t t t t t t t
t t t
( ) f t nghịch biến 1 ( ) ( )t f x f y với 1 x y đpcm
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 53/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 53 -
LUYỆN TẬP THÊM PHƯƠNG TRÌNH - BPT - HỆ
Bài 1. Cho , thay đổi luôn thỏa1
sin sin2
. Tìm GTLN và GTNN của
cos 2 cos 2 P .
Giải
Xét hệ:2 2
11 sin sinsin sin22
cos 2 cos 2 1 2sin 1 2cos P P
2 2
1sin sin
2*2 2 sin sin p
đặt
sin
: 1, 1sin
x
x y y
Khi đó:
22 2
1 12 2*
2 2 2 2 4
x y x y
x y p y xy p
1
2
2 38
x y
p xy
khi đó: , x y là nghiệm của phương trình: 2 1 2 30
2 8
p X X
Phương trình này có nghiệm thoả 1 21 1 X X
1 2 30
4 21 2 30
1 02 81 01 2 3
1 0 1 02 811 0 1 02 2
11 0 1 02 2
p
p
f p
f S
S
7
42 2 3 19
2 3 12 22 3 4
12
p p
p p p
p
1 7
2 4 p
Vậy 7 1max ; min4 2 P P .
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 54/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 54 -
Bài 2. Cho , , B C là 3 góc của 1 tam giác thỏa 2 2 2tan tan tan 22 2 2 A B C
.
CMR:4
tan , tan , tan
2 2 2 3
A B C .
Giải
Trong tam giác bất kỳ ta luôn có:
tan tan tan tan tan tan 12 2 2 2 2 2
A B B C A C
Thật vậy: ta có1
tan cot tan2 2 2
tan 2
A B C A BC
tan tan 12 2 tan tan tan tan tan tan 12 2 2 2 2 21 tan tan tan
2 2 2
A B A B B C A C
A B C
Xét hệ:
2 2 2
tan tan tan tan tan tan 12 2 2 2 2 2 *
tan tan tan 22 2 2
A B B C A C
A B C
Đặt
tan2
tan , , 02
tan
2
A x
B y x y m
C m
222 2 2 2
111*
2 2 22 2
xy y x m xy y x m xy ym mx
x y m x y m m x y xy x y xy m
2
111
1 22
142 2
2
xy x y m xy x y m
xy y x m x y m x y m
xy x y m x y m x y m
x y m
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 55/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 55 -
+ Giải 2 : Ta thấy
22
2 2
4 2 4 1 2
4 8 4 2 0,
S P m m m
m m m m m
2 vô nghiệm.
+ Giải 1 : ta có , y là nghiệm của phương trình
2
2 2
2 1 2 0
2 2 1 0 **
X m X m m
X m X m m
Vậy hệ có nghiệm
, 0 ** x y có nghiệm1 2
, 0 X X
2 2
22
2 4 2 1 003 4 0
0 2 1 02
0 2 0
m m mm m
P m mm
S m
40 4
033
2
mm
m
Vì , , y m có vai trò như nhau nên4
0 , ,3
x y m
4tan , tan , tan
2 2 2 3
A B C
Bài 3. Giải hệ phương trình: 3
3
2 3
2 3
x y x I
y x y
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 56/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 56 -
2 23 3
3 3 2 2
2 2
2 2
2 22 2
2 2
5 02 3
2 3 0
5 2 4 05 0
5 05 2 4 0
5 2 4 0
x y x xy y x y y x x y I
x y x y x y x y x xy y x y
x y
x y x y x xy y xy x xy y
x xy y x y x xy y xy
x y x xy y xy
x
2
2 22 2
2 2 0
0 1 10 1 1
0 1 10 1 1
2 1 05 5
5 05 0 5 522 4 0
vng5 0
x x x x x x
y y y y y y y
x x x y x x
x xy y x xy y y y xy x y xy
x xy y
Vậy nghiệm của hệ là 0; 0 , 1;1 , 1; 1 , 5; 5 , 5; 5
Bài 4. Tìm m để hệ phương trình: 2 12 1 x y m I y x m
có ít nhất 1 nghiệm.
Giải
ĐK: , 1 y
Đặt:2
2
1 0 1
11 0
t y y t
x uu x
khi đó:
2
2
2 1 1
2 1 2
u t m I
t u m
Lấy 1 2 vế theo vế ta có:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 57/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 57 -
2 22 0
2 1 0
12
u t t u
u t u t
u t
u t
+ TH1: u t thay vào 1 ta có: 22 2 0 *u u m để hệ I có ít nhất một nghiệm thì *
phải có nghiệm không âm, tức:
8 15 00
1
0 0402
02
m
P S m
phương trình * vô nghiệm, vậy I vô nghiệm.
+ TH2:1
2u t thay vào 1 ta có: 2 5
2 0 **2
t t m để hệ I có ít nhất một nghiệm thì
** phải có nghiệm không âm, tức:
8 19 0 1905 19 580 0
54 2 8 20
1 204
m mm
P m
mS
Bài 5. Giải các hệ phương trình:
3 3
2
3 1
2 2 2
x y x ya
x xy
Giải
Ta thấy 0 x không là nghiệm của 2 22 2 x
x x x
thay vào 1 ta có:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 58/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 58 -
33 4 2
24 2
2
2 23 2 10 8 0
1 1 15 4 0
2 14
x x x x x x x x
x x y x x
x y x
Vậy nghiệm của hệ là: 1;1 , 1; 1 , 2; 1 , 2;1 .
2 3
2
2 2 1
2 2
x y y x yb
y xy
Giải
Thay 2 vào 1 ta có:
2 3 2 3 2 2 02 2 0 2 0
2
y x y y y xy x y y xy y y x
x
+ TH1: 0 y không thỏa
+ TH2: 2 y x thay vào 2 ta có:
2 2 2 1 24 2 2 3 1
3 3 x x x x y
Vậy nghiệm của hệ là:1 2 1 2
; , ; .3 3 3 3
Bài 6. Giải các phương trình và bất phương trình:
2 11 7 1
1
xa x x
x
Giải
ĐK:1
1
x
x
- TH1: 1 khi đó:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 59/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 59 -
1 7
1 1 1 7 11 1
x x x x x x
x
1 7 x x (vô lý)
1 vô nghiệm.
- TH2: 1
+ 1 x là nghiệm của 1
+ 1 x ta có:
1
1 1 1 7 17
11
1 7
3
x
x x x x x
x x
x x
x
Vậy phương trình 1 có nghiệm là: 1; 3 x x
3 3 31 2 1 3 1 2b x x x
Giải
3 33
33
3
3 2
2
2 1 2 3 3 1 2 1 1 2 1 3 1
3 1 2 1 3 3 1 31 2 1 3 1 1
1 2 1 3 1 1
6 7 0
6 7 0
0
7
6
x x x x x x
x x x x x x
x x x
x x
x x
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 60/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 60 -
Ta có: 0 x không thỏa 1
Vậy 1 có nghiệm76
x
2 2 1 2 1 2 1 3c x x x x x
Giải
Đk: 1 x
Ta có:
2
2
2 1 1 1 1 1
2 1 1 1 1 1
x x x x
x x x x
2
2
2 2
2
3 2 1 1 1 1 2 1
2 1 1 1 2
1 1 0 1 1
9 1 4 8 43 1 2 2
1 1 0 1 1
1 4 8 41 2 2
2( )
4 13 0 4 9 54 9 5 0
2
voâ nghieäm
x x x
x x x
x x
x x x x x
x x
x x x x x
x
x x x x x x
x
02 x
1
5
42
x
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 61/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 61 -
Vậy nghiệm của phương trình là:5
14
x x
1 1 1
42 4 2
d x x x
Giải
ĐK:1
4 x
Ta có:
2
1 1 1 1 1 12 4 4 2 4 2
x x x x
1 1 1
42 4 2
1 1 1
2 4 2
1 10
4 4
x x
x
x x
Vậy nghiệm của phương trình là14
x
Bài 7. Giải các phương trình và bất phương trình:
3 2 3 2 5 1a x x x
Giải
ĐK:23
x
Đặt2
2
3 2 0 3 2
33 0
t x t x
u xu x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 62/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 62 -
2 21
1 0
1
t u t u
t u t u
t u
t u
+ TH1: t u
3 2 3
3 2 3
5
2
x x
x x
x
+ TH2: 1t u
2
3 2 1 3
3 2 3 1
3 2 3 2
17 6 0
6
x x
x x
x x x
x x x
x
Vậy nghiệm của hệ là: 51; 6;2
x x x
10
3 28 1 3 1
xb x
x x
Giải
ĐK: 0
Ta có 0 x không là nghiệm của 1
Với 0 :
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 63/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 63 -
2
10 8 1 3 12 3
8 1 3 1
2 8 1 3 1 3
2 8 1 3 2 3 1
19 3 33 3 1
4 19
313 274 39 0
1
39
313
x x x x
x x
x x x
x x x
x x x x
x x
x
x
Kết hợp với ĐK ta có nghiệm của BPT là: 1 x
21 1 1 7 3c x x x x x
Giải
Đk: 1 x
Ta có 0 x không là nghiệm của 3
Với 0 ta có:
2
2
2
2
3 1 71 1
1 11 7
1 1
1 7 1 12
6 03 (
x x x x
x
x x x x x
x
x x x x x
x x x
loaïi)
Vậy nghiệm của phương trình là 2
2 2 2
4
2 2
x xd
x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 64/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 64 -
Giải
Đk: 2 2 và 0 x
2
2
2
2 224
2 2
2 2 2 4 4
4 0 2 2
x x
x x x
x x x
x x
Kết hợp với điều kiện ta có nghiệm của phương trình là 2 0 0 2 x
2 1 1 2
3 52 1 1
x xe
x x x
Giải
Đk:1
20
x
x
2
2 1 1 3 25
2 1 12 1 1 2 2 1 1 3 2
2 1 1 0 2 1 1 0
1
21 loaïi
x x x
x x x x x x x x
x x x x
x
x
Vậy phương trình có 1 ngiệm là1
2 x
2 23 2 1 1 6 g x x x x
Giải
ĐK:
1
2
1
x
x
x
+ TH1: 1 x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 65/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 65 -
26 1 2 1 1 1
2 1 1
2 1 2
x x x x x
x x x
x x x
Ta có0
0
VP
VT
Phương trình 6 vô nghiệm.
+ TH2: 2 x tương tự 6 vô nghiệm.
Vậy phương trình 6 có nghiệm duy nhất là 1
2 22 5 3 1 2 7h x x x x x
Giải
Đk:
1
3
22
x
x
x
7 1 2 3 1 2 1 * x x x x x
+ TH1: 1 x là nghiệm của 7
+ TH2:3
2 x
2
2
* 2 3 1 1 2 1
2 3 2 1
2 1 2
0 1 0
0
1
x x x x x
x x x
x x
x x x x
x
x
Kết hợp với điều kiện ta có:
3
2 x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 66/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 66 -
+ TH3: 2 x
2
2
2
* 2 3 1 1 2 1
2 3 2 1
2 2
26 0
3
x x x x x
x x x
x x
x x x
x
Kết hợp với ĐK ta có BPT vô nghiệm.
Vậy nghiệm của 7 là3
12
x x
2 22 1 3 1 1 8i x x x x
Giải
Đk: 1 1
8 2 1 1 3 1 1 1
2 3 1 1 3 1 0
1 2 3 1 3 1 0
x x x x x x
x x x x
x x x x
3 22
1 0
2 3 1 3 1
11
04 8 6 0
4 8 6 0 (voâ nghieäm)
x
x x x
x x
x x x x
x x
Vậy phương trình có nghiệm 0 1 x
1 1 1 x x
k x x x
(đã giải ở phần trước)
Bài 8. Giải các phương trình và bất phương trình:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 67/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 67 -
2 1
2 3 11 2
x xa
x x
Giải
Đk: 2 1 x x
Đặt2
01
xt
x
2
11 2 3
13 2 0
2
21 2 11
2 4 1 222
1
voâ lyù
t t
t t t
t
x x x x x x x x
x
Vậy 2 là nghiệm duy nhất của 1
42 21 1 2 2b x x x x
Giải
Đk: 1 1 x x
Đặt 4 2 1 0t x x khi đó:
3 22
2
2
12 2 2 1 0
11 1 0
1 0
t t t t
t t t t
t t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 68/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 68 -
2 4
24 2
24 2
2
2
2 2
2
2
1
1 5 3 5 7 3 5
2 2 2
1 5(
2
1 11 1
7 3 51 5 1122
1 1 ( 1)
7 3 5 7 3 51 2 2
1 2 1 1
77 3 51
22
loaïi)
t
t t t
t
x x x x
x x x x
x x x
x x x
x x x x
x x x
Vậy phương trình có nghiệm là7
12
x x
1 1
2 31 1
x xc
x x
Giải
ĐK:1
1
x
x
Đặt1
01 x
t x
2
2
13 2
2 1 0 1
11 1 1 1
10 ( )
3 0 3
loaïi
t t
t t t
x x x x
x x
x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 69/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 69 -
Vậy 3 là nghiệm của phương trình.
2 2* 4 1 2 2 2 4d x x x x x
Giải
Đk: x
Ta có14
x không là nghiệm của Phương trình 4 .
2
2
4 3 2
22
3 2 2
2
2 2 1 14 2 ; 0
4 1 4 24 4 4
216 8 1
8 21 15 2 0 1 8 13 2 0
1
1 13 150
168 13 2 0 13 150( )
16loaïi
x x x x x x
x x x x
x x x x
x x x x x x
x
x x
x x x
Vậy nghiệm của phương trình là13 150
116
x x
2* 2 2 2 1 5e x x x
Giải
Đk:12
x
21 1
5 1 2 2 12 2
x x
Đặt 1 2 1 1 y x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 70/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 70 -
2 21 1
1 2 1 1 2 12 2
y x y x a
Theo đề ta có 2 21 1 1 1
1 1 1
2 2 2 2
x x y b
Lấy b a ta có 2 2 0x y
x y x y
+ Với 1 2 1 1 x y x x x
2
2
2 1 2 1
4 2 0
2 2
2 2 (loaïi)
x x x
x x
x
x
+ với 1 2 1 1 x y x x x
2
2
2 1 2 1
2 (voâ lyù)
x x
x
Vậy phương trình có nghiệm là 2 2 x .
2 23 5 7 3 7 2 3 7 f x x x x
Giải
Đk:2
13
x
x
Đặt2
2
3 5 7 0
3 7 2 0
t x x
u x x
Ta có hệ:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 71/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 71 -
2 2
222
22 2
2
733 32 5
22 53
3
77 3 5 73 5 733
2 23 7 2 3 7 23 3
226 59 14 0 7
26
xt u t t u
x xt ut u x
u
x x x x x x
x x x x x x
x x x
x
Vậy phương trình có nghiệm là7
226
x x
4 41 15 2 8 g x x
Giải
Đk: 15 1
Đặt4
41 0
15 0t xu x
ta có hệ phương trình:
224 4 2 2
2 2 22 2
22
16 2 2 16
2
2 2 0
02 16 04 2 2 160
t ut u
t u t u tu t u
t u
t u t u t
ut u tuut t utu
0 1 0 1
0 15
2( )
16voâ nghieäm
t x x
u x
t u
tu
Vậy phương trình có nghiệm là 1 15 x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 72/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 72 -
3 3 2 2 4 9h x x
Giải
Đk: 2 x
Đặt3
3 23 2
3t
t x x
3
3
3 2
3 2
2
2
3
29 4
3
24 4
3
2 3 16 8 16
3 24 44 0
22 22 0
22 0 ( )
3 2 2 3 6 2
voâ nghieäm
t t
t t t
t t t
t t t
t t t t
t t
x x x
Vậy phương trình có nghiệm 2
Bài 9. Giải các phương trình, bất phương trình:
4 4 4 42 2 2
2log 2 log 2 log log log 1
2 x x
xa x x x
x
Giải
Đk: 2 x
Ta có:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 73/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 73 -
42 2 2
4
42 2 2
4
4 42 2
1 1log 2 log 2 1 log
4 41 1
log 2 log 2 1 log 24 4
1 1log log log 12 4 2 4
2 1 2 1log log log 2 1
4 41
log 2 log 2 2 log log 24
x x x
x x x
x x
x x x
x x
x x x
x x
x x x
2
2
4 42 2
2
2
2 22
log log 2
2
2 1log log log log 2 2
2 4
log log 2
2
log log 2 log log 21 log *2 2
x
x x
x
x x
x
x x
x
x
x x x
Vì 2 nên ta có:
2 2* log log , 2.ñuùng x x x
Vậy nghiệm của 1 là 2 x
log 22
2 2log log 12 .3 .5 12 2 x
x xb
Giải
Đk: 2 x
2 2 2
2
log log log
log 2
2
1 12 2 3 5 12
3 25
30 900 30
log 2 4
x x x
x
x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 74/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 74 -
Vậy nghiệm của BPT là 4 x
2log 7.10 5.25 2 1 3 x xc x
GiảiĐk: 7.10 5.25 0 x x
2 13 7.10 5.25 2
5 27 5 2 *
2 5
x x x
x x
Đặt5
02
x
t
2
2* 7 5
25 7 2 0 1
5
2 51 1 0
5 2
x
t t
t t t
x
Vậy nghiệm của BPT là 1 0 x
22
4 22
1log 7 12 log 2 log 4 1 4
2d x x x x
Giải
Đk:
2
3
4
x
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 75/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 75 -
22 2 2 2
22 2
22 2
2 2
22
22 2
2
4 log 7 12 log 2 log 4 log 2
2 4log 7 12 log *
2
: 42 4
* log 7 12 log2
2 14 24 6 8
8 16 0 4 0 ( )
3
2 4* log 7 12 log
22 1
TH1
voâ lyù
- TH2:
x x x x
x x x x
x x x
x x
x x x x
x x x
x
x x x x
x
2
2
22 2
2 2
2
4 24 6 8
3 20 32 0
84
38
333 4
2 4* log 7 12 log
2
2 14 24 6 8
8 16 0 ( 4)
TH3:
ñuùng
x x x
x x
x
x
x
x x x x
x x x x
x x x
Vậy
nghiệm của BPT là8
3 3 43
x x
2 2 2 2 21 lg 1 4 2 1 .lg 1 0 5e x x x x
Giải
Đk: 1 1 x x
Đặt 2 22 1 lg 1 0t x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 76/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 76 -
2
2 2
2
2
05 4 0
4
2 1 lg 1 0
1 0 1
0lg 1 0
(loaïi)
(loaïi)
t t t
t
x x
x x
x x
Vậy nghiệm của phương trình là 1 x
3 32 8.2 6 2 2.2 1 6 x x x x f
Giải
Đặt 2 0 xt
33
3
2
8 126 6 1
2 21 1
12 0
2
2 21
(loaïi)
x
t t t t
t t t t
t t t
t
x
Vậy nghiệm của phương trình là 1 x
2 4 43 8.3 9.9 0 7 x x x x g
Giải
Đk: 4 x
24 43 3
7 1 8 9 0 *3 3
x x
x x
Đặt43
03
x
xt
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 77/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 77 -
2
4
4
4 2
2
* 9 8 1 0
1 11 0
9 9
3 0 43
3 1
3 9
3 3 4 2 ( 2)
05 0
5
(ñuùng )
(loaïi)
x
x
x
x
x x
t t
t t
x
x x x
x x x
x
Vậy nghiệm của BPT là 4 x
4 4 18.3 9 9 8 x x x xh
Giải
Đk: 0 x
4 4
4
4 4
4 4
8 8.3 9.9 9 0
3 98. 9 09 9
8.3 9 9 0 *
x x x x
x x x
x x
x x x x
Đặt4
3 0 x xt
4
2
2
4 4
4
4
1* 8 9 0
9
3 9 3
2 2 0
1
2
16
(loaïi)
(loaïi)
x x
t t t
t
x x x x
x
x
x
Vậy nghiệm của PT là 16 x
3 1125 50 2 9 x x xk
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 78/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 78 -
3
2
9 5 .25 2 .25 2.2 0
5 21 2 0 *
2 5
x x x x x
x x
Đặt5
02
x
t
2
3 2
2* 1 0
2 0 1
51 0
2
x
t t
t t t
x
Vậy nghiệm của PT là 0 x
1 11
9 6 4 0 10 x x
xl
Giải
Đk: 0 x
1 1
3 210 1 0 *2 3
x x
Đặt
1
30
2
xt
2
1
3
2
1* 1 0 1 0
1 52
1 5
2
3 1 5 1
2 2 1 5log
2
(loaïi)
x
t t t t
t
t
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 79/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 79 -
Nghiệm của BPT
32
1
1 5log
2
x
8.3 3.2 24 6 11 x x xm
Giải
11 8 3 3 2 3 3 0
3 3 13 3 8 2 0
32 8
x x x
x x x
x
x
x
Vậy nghiệm của PT là 1 3 x x
35 21 7 5 21 2 12 x x
xo
Giải
5 21 5 21
12 7 8 *2 2
x x
Đặt5 21
02
x
t
2
5 21
2
7* 8 8 7 0
5 211 021
log 775 21 7
2
x
x
t t t t
xt xt
Vậy nghiệm của PT là5 21
2
0 log 7 x x
Bài 10. Giải bất phương trình: 3 9log 1 log 4 3 4 1 1 x x x x
Giải
Đk: 0 x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 80/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 80 -
1 1 4 3 4 1 * x x x x
0 1
* 1 1 0;1
* 2 1 8 7 **
+ TH1:
(ñuùng )+ TH2: x>1
x
x
x x
Đặt 0t x
2
1** 2 1 8 7
2
14 12 8 0 2
t t t
t t t t
Kết hợp với điều kiện ta có
11 111 122 4
2 42
xt x
t x x
Vậy nghiệm của BPT là0 1
4
x
x
Bải 11. Giải phương trìn:
2
33log 1log 3 2 3 1
x x x x x x
Giải
Đk: 0 1 x
Ta có:
3 333 3
3 3
3 3
3 3
loglog 3 log .log 3 3
log log 13 3
log 3 log .log 33
1 3 3
x
x
x x x x x x
x x
x x x x x x x x x
x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 81/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 81 -
3
3 3
3
3 13
213 12
log log 1 3 133 1
2
3 13
2
(loaïi) x
x x x
x x x x x
x
Vậy nghiệm của BPT là1 3 13
2 2 x x
Bài 12. Giải phương trình: log 2 log 5 6 5 2 1 x x x x x x
Giải
Đk:65
x
2
2
2
2
1 log 2 log 5 6 5 2
2 5 6 5 2
2 9 10 2 2 5 2 0 *
2
2* 4 18 20 0
5
62
56
* 0 0 ;2
5
+ TH1:
+TH2:
(ñuùng )
x x x x x x
x x x x
x x x x x
x
x x x
x
x
x
Vậy nghiệm của BPT là6
2 55
x x
Bài 13. Giải và biện luận phương trình: log 2 log * x x m
Giải
Đk: 0 1 x
0 *- TH1: m vô nghiệm.
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 82/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 82 -
0
0 1: * 2
- TH2:
Vôùi
m
x m
Nếu 2 *thìm có vô số nghiệm
Nếu 0 2 *thìm vô nghiệm 1: * 2Vôùi x m
Nếu 2 *thìm vô nghiệm
Nếu 0 2 *thìm có vô số nghiệm.
Bài 14. Giải các phương trình:
2 4log 4 log 5 0 1a x x
Đk:
1
1
x
x
Đặt 4log , 0.t x t
24 2 21log log log
2t x x x .
Khi đó
2
4 4
25 25
11 4 5 0
5
log 5 log 25
4 4 .
loaïit t t
t
x x
x x
Vậy nghiệm của pt đã cho là: 254 .
2 12 1 23 3 1 6.3 3 2 x x x xb
22
2
2 3.3 9.3 3.3 1
3.3 9.3 3.3 1 *
x x x
x x x
Đặt 3 , 0 xt t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 83/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 83 -
2* 3 9 3 1 **t t t
- TH1:1
3t
2
3
** 3 12 1 0
6 33
3
6 33
3
6 33 6 333 log .
3 3
loaïi
x
t t
t
t
x
- TH2:1
0 .3
t
2** 3 6 1 0
3 2 3
3
3 2 3
3
loaïi
loaïi
t t
t
t
Vậy nghiệm của pt đã cho là: 3
6 33log .
3 x
2 5 24 5 7 5 7 x x xc
Bài 15. Giải và biện luận phương trình:
12 2
1 1 1
x a a a x
x x
Giải
Đk: 0 x
0 : 1 x thỏa 0a
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 84/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 84 -
2 2 2
22 2
2
2
0
1 1
1 1
2 1
4 1
1 0 1 ( ).
1 0 1
voâ lyù
(phöông trình voâ nghieäm).
x
x a a a x
x a a x a a
a x a
x a
a a
a a
Vậy phương trình có nghiệm 0, 0a
Bài 16. Giải các hệ:
11
2
3 2
x y y xa I
x y x y
Giải
Đk: 0, 0 x y
Ta thấy 0, 0 x y
là một nghiện của hệ.
Với 0 y , đặt , 0 x t y t ta có:
2
2
11'
2
3 2'
t y y y t y I
t y y t y y
Chia 1' cho 2' vế theo vế ta được:
22 2 2
2
2 4 2 4 2
2
2
16 1 1
61
6 6 5 6 0
3
33
2 2
2
loaïi
loaïi
t t t t t
t t
t t t t t t
t
t t
t t
t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 85/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 85 -
+ 3 3 3t x y x y . Thay vào 1 ta được:
1 3 3 32 3
2 4 4 y y y y x .
+ 2 2 2 .t x y x y Thay vào 1 ta được:
23 2 3 2.
2 y y y y x
Vậy nghiệm của hpt đã cho là:3 3 3 2
; , ; 2 .4 4 2
13 3
12 8
x x y y
b II
x y y
Giải
Đk:
10
3 0
x y
x y
Đặt1
, 3; 0, 0t x u x y t u y
.
22 2
33 325 2 5
t ut u t u II
tut u t u tu
,t u là 2 nghiệm của phương trình:
2
1
213 2 0
2 2
1
t
u X X X
X t
u
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 86/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 86 -
1 11 11
273 2
2 10 ; 3 103 10
2 10; 3 10
3 10
x xt y y
u x y x y
x y
x y
1 12 42
1 43 1
3; 1
5; 1
x xt y y
u x y x y
x y
x y
Vậy nghiệm của hpt đã cho là: 2 10 2 10
; 3 10 , ; 3 10 , 3;1 , 5; 1 .3 10 3 10
2 2
14
84
x y xyc III
x y xy
Giải
Đk: 0. xy
Đặt , ; 0.u xy v x y u
2 2
14 14
684
10 164
4 1010
v u v u III
v uv u
v xy xy
u x y x y
, x y là 2 nghiệm của phương trình:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 87/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 87 -
2 810 16 0
2
X X X
X
Vậy nghiệm của hpt đã cho là: 8; 2 , 2; 8 .
2 23 3
3 3
2 3
6
x y x y xyd IV
x y
Giải
Đặt 3 3,t x u y
3 3
22 2
2 3
6
2 3 62 9
866
t u t u tu IV
t u
t tu u tu t ut u tu
tut ut u
Vậy ,t u là nghiệm của phương trình
2
3
3
3
3
46 8 0
2
2 8
4 64
64482
X X X
X
x x
y y
x x y y
Vậy nghiệm của hpt đã cho là 8; 64 , 64; 8
3 3 65
12
10 2
x y xye
x y
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 88/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 88 -
Đk: 0 xy
- Nếu 0 y không là nghiệm của hệ.
- Nếu 0 y đặt x ky ta có:
263 3
3 6
51
25
1 *2
ky y ky
k k
Đặt 6 0t k
6
26
2 2
5* 1 0 1 122 2
2
13128
64 6413
1 1128
64 6413
213
t k
t t t k
x
yk x y
k x y x
y
Vậy nghiệm của hpt đã cho là2 128 128 2
; , ;13 13 13 13
lg lg
lg 4 lg 3
3 4
4 3
x y
f V x y
Giải
Đk: , 0 x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 89/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 89 -
2 2
2
2 2 2
2
2 2 2 2
lg lg3 lg lg 4
lg 4 lg 4 lg lg3 lg3 lg
lg lg3 lg lg 4
lg 4 lg 4lg lg 3 lg3lglg lg3lg 4 lg lg 4
lg3lg 4lg lg 3lg lg 3 lg 4 lg3
lg lg3lg 4 lg lg 4
lg lg 4 lg 3 lg 3 lg 4 lg 3
1lg lg3
3
x yV
x y
x y
x y x y
x y
x y
y
y y x
1
4
Vậy nghiệm của hpt đã cho là1 1
;4 3
2 2
2 3
1
log log 1
x y g VI
x y x y
Giải
Đk: y y
2 3
1 1
log log 1 2
x y x yVI
x y x y
Đặt 0t x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 90/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 90 -
62
6
66
66
6
2 3
2 3
2 3 3
32 2
1
log 2log 6
log 2log 2
log 2
log 2log 2log 2
12 log log 1
log log 1
log 3log log 1
1 1log
log 3 1 log 6
3 3
13
332
1 13.33
32
t t
t t
t t
t
t
x x y
x y
y
Là nghiệm của hệ.
3 3
2 2
3 3 1
1
y x x y xyh VII
x y
Giải
2 2
2 2
2 2
2 2
2 2
2 2
2 2
3 3 1
1
1 3 3 1
1
1 3 3 0
1
1*1
13 3 0
3 3 0**1
1
y x
y x
x y
x y
x y
x y x xy y xyVII
x y
x y xy xy
x y
xy x y
x y
xy xy
x y x y
x y x y
x y
- Ta giải *
+ 0 x không là nghiệm của *
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 91/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 91 -
+ 0 * x vô nghiệm
- Giải ** : Thay ** vào VII ta có: 3 3 1 x y x y xy
2 2
2 2
2 2
01 0 1
11
1
1
2
0 1
1 0
x y x y x y xy x y
x y xy x y
x y
x y
x x
y y
Là nghiệm của hệ.
2 21 1
1 1
log 1 2 log 1 2 4 1
log 1 2 log 1 2 2 2
x y
x y
y y x xk
y x
Giải
Đk:1 1, 021
1, 02
x x
y y
1 1
1 1
11
1
1 1
2
2
1 2log 1 2log 1 4
log 1 log 1 2
1log 1 2
log 1
log 1 1
2
1 2 log 1 2 2
1 2 1 2 1
0 05 2 0 2 2
5 5
thay vaøo ta coù
log
x y
x y
x x
x
y y
y x
y x
y y
y
x y
y y
y y y
y x y y
y x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 92/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 92 -
Vậy hệ phương trình có 2 nghiệm là 2 2
0,0 ,5 5
5
log 1
2log log
xy
x y
x y
m VIII xy xy
Giải
Đk:
1
0
1
xy
x y
x y
2
2 2 2
2 2
2 2 2 2
2 2
2 2
2
2 1
log 5 log
log log 5
5 52
4 5 0 *
1* : 4 5 0
5
5 5 5 0
5 5
loaïixeùt
xy xy
xy xy
x y xyVIII
x y
x y x y
x y
x y x y x y x y
x y x y x y x y xy
x y xy
xy x y xy
xy
xy y y
x y x y
5 5 5 52 2
5 5 5 5
2 2
loaïi vì
y y x y
x x
Vậy hệ phương trình có nghiệm là:5 5 5 5
;2 2
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 93/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 93 -
222 3 log 3 4
2
2 3 1
4 1 3 8 2
x x y
n y y y
Giải
22 2
22
1 2 3 log 3 4 .log 3
2 3 3 .log 3
x x y
x x y
Đk: 3 y
2
2
2 4 1 6 9 8
3 0
3 0
3 thoûa maõn heä phöông trình
y y y y
y y
y
y
2 13 2 3 0
3Vôùi ta coù
x y x x
x
Vậy hệ có nghiệm 1; 3 3; 3
1 2 1
4
4 3.4 2 13 2 log 2 2
x y y
p x y
Giải
1
2 3 22
x y
Vì 1 2 14 0, 3.4 0 x y y nên áp dụng bất đẳng thức cauchy ta có:
1 2 1 3 2
1 2 1
14 3.4 2 3.4 2 3. 2
2
4 3.4 2
x y y x y
x y y
Mâu thuẫn với 1 . Vậy hệ vô nghiệm.
PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 94/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 94 -
1. CÁC HỆ CƠ BẢN
a. Hệ đối xứng loại I
(2004-D) Tìm m để hệ sau có nghiệm: 1
1 3
x y I x x y y m
Giải
Đặt:0
0
u x
v y
3 3
1
*1 3
1
u v
I u v m
u v
uv m
Khi đó ,u v là nghiệm của phương trình
2 0 ** X X m
Hệ đã cho có nghiệm ; * x y
có nghiệm 0, 0 **u v
có 2 nghiệm dương:
1 4 01
1 0 04
0
m
S m
P m
Bài tập tương tự:
Bài 1. Tìm m để hệ sau có 2 nghiệm:
2 2
2
2 1
4
x y m I
x y
Giải
2
2
2 2 1*
4
x y xy m I
x y
Đặt ,t x y u xy
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 95/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 95 -
2
2
2 2 1 2*
14
t u m t
u mt
Điều kiện để hệ có nghiệm là:
2 4 0 4 4 1 0
0
t u m
m
Khi đó , y là nghiệm của phương trình:
2
2
2 1 0
2 1 0
X X m
X X m
Cả 2 phương trình đều có ' m
Để hệ chỉ có 2 nghiệm thì 0m
Khi đó 1
2
1
1
X x y
X x y
Vậy hệ có 2 nghiệm khi 0m và 2 nghiệm đó là 1;1 , 1; 1
Bài 2. Tìm m để hệ sau có 4 nghiệm: 2 2 22 1 x y xy m I
x y xy m m
Giải
Đặt ,S x y P xy
2
2 1S P m I
SP m m
Khi đó ,S P là nghiệm của phương trình
2 22 1 0 * X m X m m
Có 1 0 * có 2 nghiệm phân biệt là 1 1 1
2 2 2
1 1,
, 1
X m S m P m
X m S m P m
Để hệ I có 4 nghiệm thì:
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 96/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 96 -
2 21 1
2 22 2
4 0 6 1 0
4 0 4 4 0
3 2 3 2
2
S P m m
S P m m
m m
m
Bài 3. Cho , ,a b c thay đổi thỏa: 2 2 2 2
1
a b c I
ab bc ca
CMR:
4 4, ,
3 3a b c
Giải
2 22 2
1
a b ab c I
ab a b c
Đặt ,S a b P ab ta có:
2 2
2 2
22 2
2
2 2
1
2 1 2
1
22112 4 0
1 22
1 1
S P c
P Sc
S Sc c
P Sc
S cS c P c P ScS Sc c
P Sc S cS c
P Sc P c
Điều kiện để hệ I có nghiệm là
2
2 2 2
2 2 2
4 0
02 4 1 0 3 4 0 343 4 02 4 1 0 03
4 4;
3 3
S P
cc c c c
c cc c c
c
Vì vai trò của , ,a b c như nhau nên ta có :4 4
, ,3 3
a b c
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 97/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 97 -
Bài 4. Cho , thay đổi luôn thỏa1
sin sin2
. Tìm GTLN và GTNN của
cos 2 cos 2 P .
(Đã giải)
b. Hệ đối xứng loại II.
(2003-B) Giải hệ phương trình:
2
2
2
2
23
23
y y
x I
x x
y
Giải
Đk: 0, 0 x y khi đó:
2 2
2 2 2 2
2 2
2 2
3 03 2
3 2 3 2
3 23 0
3 2
1
1
voâ nghieäm
x y xy x y x y y I
xy x xy x
x y
xy x xy x y
xy x
x
y
Vậy nghiệm của hệ là 1;1
Bài tập tương tự:
Bài 1. Giải hệ phương trình:3
3
2 3
2 3
x y x
y x y
(Đã giải)
Bài 2. Tìm m để hệ phương trình:2 1
2 1
x y m
y x m
có ít nhất 1 nghiệm.
(Đã giải)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 98/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 98 -
c. Hệ đẳng cấp bậc hai.
Bài 1. Giải hệ phương trình:
2 2
2 2
2 3 4 1
3 3 2
x xy y
x xy y
Giải
+ 20 : 1 4 x y vô nghiệm.
+ 0 x đặt y tx khi đó hệ
2 2 2 2
2 2 2 2
2 2
2 2
2 3 4
3 3
3 2 4 3
3 1 3 4
x tx t x
x x t t x
x t t
x t t
VP của 3 0 nên VT của 3 0
Chia 4 cho 3 ta có:
2
22
2
3 1 3 15 13 2 0 153 2 41
t t t t t t t t
+ với 1t 2
15t ta có hệ:
2
1
11
x y x
y x
+ với2
15
t ta có hệ:
2
228915
225 1589 89
y y x
x x
Vậy hệ có nghiệm là 15 2 15 2
1;1 , 1; 1 , ; , ;89 89 89 89
Bài 2. Tìm m để hệ phương trình:
2 2
2 2
3 4 1
3 2 2
x xy y m
x xy y m
có 4 nghiệm.
Giải
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 99/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 99 -
+ Nếu 0 từ 22 2 y m , với 2 0m x không là nghiệm của phương trình.
+ 0 x , đặt y tx hệ trở thành
2 2 2 2
2 2 2 2
2 2
2 2
3 4 33 2 4
1 3 4
3 2
x x t t x m x x t t x m
x t t m
x t t m
VP của 4 0 nên VT của 4 0 . Chia 2 vế của 3 cho 4 ta có:
22
2
3 1 43 5 2 5 0 *3 2
t t mt m t mt t m
Để hệ có 4 nghiệm phân biệt thì * phải có 2 nghiệm phân biệt tức là
2 34 35 0 2 35m m m m
Vậy phương trình có 4 nghiệm khi 2 35m m
d. Một số hệ khác.
(2003-A) Giải hệ phương trình:
3
1 11
2 1 2
x y x y
y x
Giải
Đk: , 0 x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 100/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 100 -
3
3
34
2 24 2 2
11 1 0
1
2 1 02 11
1
2 12 0
1
1 5
2
1 5
21
1 1 32 0,
2 2 2
voâ nghieäm
x y x y
xy xy
x y x y
x x y x
xy y x
y x x x
x y
x y
x y
y x
x x x x x
Vậy nghiệm của hệ là 1 5 1 5 1 5 1 5
; 1;1 ;2 2 2 2
.
(2006-D) Chúng minh với 0a , hệ:
ln 1 ln 1 x ye e x y
I y x a
có nghiệm duy nhất.
Giải
ln 1 ln 1
ln 1 ln 1 0 1
2
x y
a x x
e x e y
I y x a
e a x e x
y x a
Hệ I có nghiệm duy nhất khi 2 có nghiệm duy nhất trên 1; .
Đặt ln 1 ln 1a x x f x e a x e x
1 11 1
a x x f x e e x a x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 101/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 101 -
Vì 0 1a x ta có:
0
1 10
1 10, 1
a x xe e
x a x f x x
f x đồng biến trên 1;
I có nghiệm duy nhất trên 1;
Bài tập tương tự:
Bài 1. Giải hệ phương trình: 3 3
2 2
3 3 1
1
y x x y xy
x y
(Đã giải)
Bài 2. Giải các hệ phương trình:
3 3
2
3
2
x y x y
a x xy
(Đã giải)
2 3
2
2 2
2
x y y x yb
y xy
(Đã giải)
PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH CHỨA CĂN
Bài 1: Giải phương trình và b t phương trình :
a) 2 11 ( 7)
1
x x x
x
b) 3 3 31 2 1 3 1x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 102/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 102 -
Giải:
a) 2 11 ( 7)
1
x x x
x
(1)
Đk: 1 1x x
Từ (1) ( 1) 1 ( 7) 1x x x x
1
11 7
x x
x x
Thế 1x vào phương trình (1) ( thoả mãn).
Vậy nghiệm của PT (1) là 1x
b) 3 3 31 2 1 3 1x x x (1)
Ta có: (1) 3 331 2 1 3 ( 1)(2 1)( 1 2 1) 3 1x x x x x x x
33 ( 1)(2 1)(3 1) 3x x x
( 1)(2 1)(3 1) 1x x x 2(6 2 9) 0x x x 0
1 55
6
x
x
Thử lại ta thấy1 55
6x
( thỏa mãn)
Vậy phương trình(1) có 2 nghiệm1 55
6x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 103/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 103 -
c) 2 2 1 2 1 2 1x x x x x (*)
Đk: 1x
Từ (*) 2 1 1 1 1 2 1x x x 2 1 2 1 1 2 1 (1)
2 2 1 1 1 2 1 (2)
x x x
x x x
+Giải (1): (1) 23 1 2 2 4 13 0x x x x phương trình vô nghiệm
+Giải (2): (2) 2
11 2 2 4 9 5 0 5
4
x
x x x x x
Thế 1x ;5
4x vào phương trình (*); 1x thoả mãn
Vậy nghiệm của phương trình (*) là 1x .
d)1 1 1
2 4 2x x x (1)
Đk: 14
x
Ta có:1 1 1
2 4 2x x x
1 1 1 1
4 4 4 2x x x
1 1 1
4 2 2x x
1 1 1
4 2 2x
1
04
x 1
4x .
Thay1
4x vào phương trình (1) thoả mãn nên
1
4x là nghiệm của pt (1)
Bài 2: Giải phương trình và b t phương trình :
a) 3 2 3 2 5x x x b) 10 38 1 3 1
x x x x
c) 2( 1 1)( 1 7)x x x x x d)2 2 2
2 2
x x
x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 104/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 104 -
Giải:
a) 3 2 3 2 5x x x (1)
ĐK:2
3x
Ta có: (1) 3 2 3 3 2 ( 3)x x x x
Đặt 3 2 0u x , 3 0v x
Ta có hệ2 2
2 2
3 11u v
u v u v
2 23 11
( )( 1) 0
u v
u v u v
2 23 11
1 0
u v
u v
u v
2 2
2 2
(2)3 11
1 0(3)
3 11
u v
u v
u v
u v
+)Giải(2): (2) 2 2
113 2
11 23 11 2 11
32
x u v u v
v v x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 105/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 105 -
113 2 52
11 23
2
x x
x
+)Giải(3): (3) 2 2 2
11 1 1
22(1 ) 3 11 6 0
3 ( )
u v u v u v u
v v v v v v
v l
(loại)
Vậy phương trình (1) có nghiệm là5
2x
b) 10 38 1 3 1
x x x x
(1).
ĐK:1
8x
Ta có: (1) 8 1 3 1 10
38 1 (3 1)
x x x x
x x
(vì 8 1 3 1 0x x )
2 8 1 3 1 3x x x
4 11 2 2 (8 1)(3 1) 3x x x x
8 (8 1)(3 1) 43 5x x x
2
2
43 5 0
64(8 1)(3 1) (43 5)
5
43313 274 39 0
5
43 139
1313
x
x x x
x
x x
x x
x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 106/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 106 -
Vậy tập nghiệm của bất phương trình (1) là: 1;
c) 2( 1 1)( 1 7)x x x x x (1)
Đk: 1x
Ta có: (1) 2 21 ( 6) 1 7x x x x x x x
2( 6)( 1 1) 0x x x
2 6 0x x ( do 1 1 0x )
2 ( )
3 ( )
x n
x l
Vậy nghiệm của của PT là : 2x
d)2 2 2
2 2
x x
x x x
Đk: 2;2 \ 0x
Ta có:2 2 2
2 2
x x
x x x
2
2 2 2
2
x x
x x
22 2 2 4 4
02
x x x
x
24
0x
x
0;2x
Vậy tập nghiệm của BPT là: (0;2]
e)1 2 1 2
31 2 1
x x
x x x
(1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 107/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 107 -
Đk:1; \ {0}
2x
Ta có : 1 2 1 231 2 1
x x x x x
2
1 2 1 3 2 0x x x x
1 2 1 2 (1 2 )( 1) 3 2
0x x x x x
x
2 (1 2 )( 1)
0x x
x
(1 2 )( 1) 0x x
1
21
x
x
Ta thấy 1x không thỏa mãn phương trình
Vậy nghiệm của phương trình (1) là1
2x
g) 2 23 2 1 1x x x x (*)
Đk: ( ; 2] [1; ) { 1}x
Đặt2 2 2
2
3 2 01
31 0
u x x u v x
v x
Khi đó PT (*) trở thành:
2 2
( ) 1 03 3
u v u v
u v u v
(1)
3 (2)1 03
u v u v u v u v
+ Giải (1): (1) 0 1u v x ( nhận)
+ Giải (2): 2 2(2) 3 2 3 1x x x 2 2 23 2 9 ( 1) 6 1x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 108/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 108 -
2
2 2
21 2
4( 1) 4 4
x x x
x x x
222
2 2 73 4 8 03
x x
x x x
vô
nghiệm
Vậy PT (*) có nghiệm duy nhất: 1x
h) 2 22 5 3 1 2x x x x x (1)
Đk:
; 2 1;3
; 2 ; {1}32; 1 ;
2
x
x x
Ta xét các trường hợp sau:
+) TH1: 1x là nghiệm của (1)
+) TH2: 2x : (1)
1 . 3 2 1 . 2 ( 1x x x x
+) TH3:3
2x : (1) 1 2 1 2 3 0x x x x
1 . 3 2 1 1 . 2
3 2 1 2 ( 1 0)
3 2 . 1 3
x x x x x
x x x do x
x x x
( vô nghiệm vì VP 0 VT 0 )
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 109/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 109 -
2 1 2 3 0x x x ( 1 0)do x
2 1 2 3x x x
2 1 2 ( 2)( 1) 2 3x x x x x
2 ( 2)( 1) 4x x (vô nghiệm)
Vậy bất phương trình có duy nhất nghiệm: 1x
k)1 1 1x x
x x x x
Đk:
10
1 0 11
1 0
x x x x
x
+)Với 1x thìBPT:
2
2
2 2
2 2
22
( 1)1 1 1
11 1
( 1) 1
2 1
2 1 0
1 0.
x x x x
x x x x
x x
x x x x
x x x x x x
x x x x
x x
Đúng 1x
+)Với 1 0x ,ta có: 1x
1 11
1 11
1 11 0
x x x
x x x
x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 110/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 110 -
Mà1
0; [ 1;0)x
x x
.Suy ra BPT đã cho vô nghiệm.
Vậy nghiệm của BPT đã cho là : 1x
m) 2 22 1 3( 1 1 )x x x x (1)
Đk: 1;1x
Ta có: (1) 2 2 2 21 2 1 1 3( 1 ) 3x x x x x x
2 2 2( 1 ) 1 3( 1 ) 3x x x x (2)
Đặt 21t x x , PT (2) trở thành: 2 3 2 0t t 1
2
t
t
+ Với 1t 21 1x x 1
0
x
x
+ Với 2t 21 2x x 22 4 3 0x x (vô nghiệm )
Thử lại ta thấy1
0
x
x
thỏa mãn
Vậy phương trình có nghiệm1
0
x
x
Bài 3. Giải phương trình và b t phương trình:
a)2 1
2 31 2
x x
x x
b)
42 21 1 2x x x x
c)1 1
21 1
x x
x x
d) 2 2(4 1) 2 2(2 )x x x x x
e) 2 2 2 2 1x x x f) 2 23 5 7 3 7 2 3x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 111/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 111 -
Giải:
Cách 1:
a)2 1
2 3
1 2
x x
x x
(1)
Đk: ; 2 1;x
Đặt2
01
x t
x
, PT trên trở thành:
23t
t 2 3 2 0t t
1
2
t
t
+) Với 1t 2
1
1
x
x
2 1x x Vô nghiệm
+) Với 2t 2
21
x
x
24
1
x
x
2 4 4x x 2x
Vậy phương trình có nghiệm 2x
Cách 2:
(1) 2 2
2 14 4 9
1 2
2 4 1 5 1 2 0
9 18 0
2
x x
x x
x x x x
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 112/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 112 -
b) 42 21 1 2x x x x (1)
Đk: 1x
Vì 2 24 1 1 1x x x x nên 4 2
24 2
1(1) 1 2
1
x x
x x
Đặt 4 2 1 0t x x ; PT trên trở thành:2
12t
t 3 2 1 0t t
1 (2)
1 5 (3)2
1 50
2
t
t
t
+) Giải (2): 1t 4 2 1 1x x 2 1 1x x 2 21 1 2x x x 1x
+) Giải (3):1 5
2t
4 2 1 5
12
x x
4
216 1 1 5x x
22 2 1 7 3 5x x
2 24 4 94 42 5 4 7 3 5 4x x x
49 21 5 7
214 6 5x
Thử lại ta có 1x và7
2x thoả mãn (1)
( loại )
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 113/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 113 -
Vậy 1x và7
2x là nghiệm của (1)
c)1 1
21 1
x x
x x
Đk: 1 1x
+ Đặt1
1
x t
x
12t
t 2 2 1 0t t 1t
11
1
x
x
1 1x x
2 2 1 1x x x
2 3 0x x
0
3
x
x
Thử lại ta có 3x thỏa mãn
Vậy phương trình có nghiệm là x 3
d) 2 2(4 1) 2 2(2 )x x x x x (1)
TXĐ: D
Ta có: (1) 2 2(4 1) 2 4 2x x x x x
2 2 2(4 1) 2 3 2 2x x x x x x x (2)
Đặt
2
2 0t x x , PT(2) trở thành:
2 2
(4 1) 3 2 0t x t x x ;
Ta có 2(2 3)x nên PT trên có nghiệm1 (3)
3 2 (4)
t x
t x
+) Giải(3): 1t x 2 2 1x x x 2 22 2 1x x x x
x =1
+) Giải(4): 3 2t x 2 2 3 2x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 114/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 114 -
2 29 12 4 2x x x x
28 13 2 0x x
13 105
1613 105
16
x
x
Thử lại ta có x 1 ,13 105
16x
thỏa mãn
Vậy nghiệm của phương trình (1) là x =1,
13 105
16x
e) 2 2 2 2 1x x x
Đk:1;
2x
Ta có 2 2 2 2 1x x x 2
2 2 1 1 1x x (1)
Đặt 1 2 1y x , 1y , Ta đưa về hệ :
2
1 2 1
2( 1) 1 1
y x
y x
2
2
1 2 1
1 2 1
y x
x y
2
2 2 0
1 2 1
y x y x y x
x y
2
0
1 2 1
y x y x
x y
2
1 2 1
x y
x y
x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 115/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 115 -
2
2
1 2 1
1 2 1
x y
x y
x y
x y
2
2
(2)1 2 1
1 2 1
(3)
x y
x x
x x
x y
+) Giải (2): ta thấy 2 2x y không thỏa mãn nên 2 2x y là nghiệm
+) Giải (3): Vô nghiệm
Vậy nghiệm của phương trình là 2 2x
f)2 2
3 5 7 3 7 2 3x x x x (1)
Ta có: (1) 2 23 5 7 3 3 7 2x x x x
2 2 23 5 7 9 3 7 2 6 3 7 2x x x x x x
26 3 7 2 4 2x x x
2 236 3 7 2 16 16 4x x x x
226 59 14 0x x
2
7
26
x
x
Thử lại nghiệm ta có7
26x , 2x thỏa.
Vậy nghiệm của phương trình là 726
x , 2x
g) 4 41 15 2x x (1)
Đk: 15;1x
Đặt4
4
1 0
15 0
u x
v x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 116/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 116 -
PT(1) qui về hệ sau: 4 4
2
16
u v
u v
2 2 2 2
2
2 16
u v
u v u v
22
2 2
2
2 2 16
u v
u v uv u v
22 2
2
4 2 2 16
u v
uv u v
2
0
8
u v uv
uv
2 0
0 22
02 2
8 0
u v u
uv v u v
uv u v u
uv v
+) Với4
4
0 1 0 1 01
2 15 1615 2
u x x x
v x x
+) Với4
4
2 1 2 1 1615
0 15 015 0
u x x x
v x x
Vậy nghiệm của phương trình là 1x , 15x
h) 3 3 2 2 4x x (1)
Đk: 2;x
Đặt
3 3 2
2 0
u x
v x
PT (1) đưa về hệ sau: 2 3
4
3 4
u v
v u
23
4
3 4 4
v u
u u
3 2
4
3 24 44 0
v u
u u u
32 3 2 2 3 2 82
2 2 42 2
v x x x
u x x
Vậy nghiệm của phương trình là 2x
vô nghiệm
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 117/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 117 -
Biến đổi cơ bản:
Giải:
Điều kiện: 3
9
log (9 72) 0 9 72 1log 73
0 1 0 1
x x
x x x
Ta có: (1)3
log log (log (9 72))x
x x x
3
3
9
3
( 1)( log (9 72)) 0
1 0(*)
log (9 72) 0
1 0( ì log 73)
log (9 72) 0
x
x
x
x x
x
x
x vn v x
x
Giải (*) và kết hợp với điều kiện ta được:9
9
1
0 2 log 73 2
log 73
x
x x
x
Vậy nghiệm của bất phương trình là:9
log 73 2x .
Giải:
Ta có: (1)2
2 (2 4.2 ) (2 4) 0x x x x
(2002-B) Giải bất phương trình:3
log (log (9 72)) 1x
x (1)
(2006-D) Giải phương trình:2 2 2
2 4.2 2 4 0x x x x x (1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 118/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 118 -
2
2
2
2
(2 4)(2 2 ) 0
2 4 1
02 2
x x x
x
x x
x
x
Vậy1
0
x
x
là nghiệm cần tìm.
Giải
Pt 3 2 2 33.2 4.2 .3 3 .2 2.3 0x x x x x x
Nhận thấy 33 x không là nghiệm của Pt, ta chia hai vế của Pt cho 33 x , ta được:
3 22 2 2
3. 4. 2 03 3 3
2 2
3 31
21 loai
3
x x x
x
x
x
Vậy x =1 là nghiệm cần tìm.
BÀI TẬP TƯƠNG TỰ:
Giải:
Điều kiện:
6
0 1 1 5
log 6 0x
x
x x
x
(2006-A) Giải phương trình: 3.8 4.12 18 2.27 0x x x x
1. Giải phương trình: 6
log log 6 0x x
x (1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 119/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 119 -
Nhận xét: 16
x khi 1 5x nên (1) log 6 1 log
x x x x
( 1)( 6 ) 0
2 5
x x x
x
Vậy nghiệm của (1) là 2 < x < 5.
Giải:
Điều kiện: x1
Ta có: (1) log2 2
2
log
log 3
x + log3(log2x) = log2(log2x)
log2(log2x) – log2(log23) + log3(log2x) = log2(log2x)
log3(log2x) = log2(log23)
log2x = 3log2
(log2
3)
x =log (log 3)
2 232 >1
Vậy x =log (log 3)
2 232 là nghiệm của (1).
Giải:
Điều kiện: 3 2
3 2
0 1
2 1 0
0 2 1
4 4 0
x
x
x x
x x x
0 1x
Ta có: (1) 2
(2 1)
1 2log (2 1) 2 log (2 1) log [ (2 1)]x
x x
x x x x
2. Giải phương trình : log2(log3x) + log3(log2x) = log2(log2x) (1)
3. Giải phương trình : 3 2
3 2
2log (2 1) log (4 4 )
x x x x x x x
(1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 120/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 120 -
1 2log (2 1)
2 log (2 1) 21
log (2 1)
x
x
x
x x
x
2log (2 1) 1
log (2 1) loglog (2 1) 11log (2 1) 1 log (2 1) log
x
x x x
x x x
x
x x x
x x x
( 1)(2 1 ) 0 1
1 1( 1)(2 1 ) 0
2
x x x x
x x x x
Kết hợp với điều kiện ta có nghiệm của (1) là:1
2x .
Giải:
Ta có: (1)2 2 2 1 3
2 .3 .5 2.3 .5x x x x
2
2
1 2 3 2 2
1 2 3 2 2
2 2 2
2 2
2 2
2 2 2
2 2
2
2 .3 .5 1
log 2 log 3 log 5 0
1 ( 1)( 3) log 3 2( 1) log 5 0
( 1)[1 ( 3) log 3 2 log 5] 0
( 1)( log 3 3 log 3 2 log 5 1) 0
3 log 3 2 log 5 1
1 log 3
x x x x
x x x x
x x x x
x x
x x
x
Vậy tập nghiệm của bpt là 2 2
2
3 log 3 2 log 5 11;
log 3
10. Giải bất phương trình : 3 9log 1 log 4 3 4 1x x x x (*)
4. Giải bất phương trình :2 2 2 12 .3 .5 270x x x x (1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 121/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 121 -
Giải:
Đk: 0x
Ta có: (*) 3 3
1log 1 log 4 3 4 12x x x x
2
3 3log 1 log 4 3 4 1x x x x
2
1 4 3 4 1x x x x (1)
Đặt 1 1t x x , khi đó PT(1) trở thành:2
4 3 0t t
1
3
t
t
+)Với 1t 1 1x x 0;1x
+)Với 3t 1 3x x 4;x
Vậy tập nghiệm của bất phương trình là 0;1 4;x
Giải:
Đk: ; 3 0;1x
Ta có: (*)
2
2
3 33
log 3 log log 1x x
x x x x
3 3log log 1x x
1x x 1
2x
Giải:
11. Giải phương trình :
233
log 1log 3 2 3x x x
x x x
(*)
12. Giải phương trình : log 2 log 5 6 5 2x x
x x x x (*)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 122/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 122 -
Đk: 0 1x
Ta có: (*) 2
log 2 log 5 6 5 2x x
x x x x
22 5 6 5 2x x x x
Đặt 2 0t x x , PT trên trở thành: 2 5 6t t 2 5 6 0t t 2
3
t
t
+) Với 2t 2 2x x 0x
+) Với 3t 2 3x x 52x
Thử lại ta có 0x ,5
2x thỏa.
Vậy nghiệm của phương trình là 0x ,5
2x
Giải:
+) 0m : Bất phương trình vô nghiệm
+) 0 2m : Tập nghiệm của bất phương trình 1;S
+) 2m : Tập nghiệm của bất phương trình 0;1S
ĐẶT ẨN PHỤ
Giải:
a) Với m=2, ta có: 2 2
3 3log log 1 5 0x x
13. Giải và biện luận bất phương trình : log 2 logx x
m
(2002-A) 2 2
3 3log log 1 2 1 0x x m (1)
a) Giải (1) khi m=2
b) Tìm m để (1) có ít nhất một nghiệm thuộc 31;3
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 123/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 123 -
2 2
3 3
2 3
3 3
32
33
log 1 log 1 6 0
log 1 3 ( ) log 3 3
3log 3log 1 2
x x
x loai x x
x x x
b) Ta có: 3 2
31 x 3 1 log 1 2x
Đặt f( 2
3log 1x ) = 2 2
3 3log 1 log 1 2 2x x m
Khi đó: f(1).f(2)03
(3 2 ) 0 02
m m m
Vậy với 30;2
m thì thỏa mãn đề ra.
Giải:
Ta có: (1) 2
5 54
4 144log log [5(2 1)]
2
x x
2
4
2 4 2 4
2
2
4
4 1445(2 1)
22 144 2 .5.2 2 .5 0
2 20.2 64 0
2 22 4
2 2
x x
x x
x x
x
x x
Vậy nghiệm của (1) là: 2< x <4.
BÀI TẬP TƯƠNG TỰ:
(2006-B) 2
5 5 5log (4 144) 4 log 2 1 log (2 1)x x (1)
1. Giải phương trình:
a) 2 2log 2. log 2. log 4 1x x x (1) b) 3 92. log 3 log 3 log 3 0x x x (1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 124/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 124 -
Giải:
a)2 2
log 2. log 2. log 4 1x x
x (1)
Điều kiện: 0 1x
Ta có: (1)2
2 2
1(2 log ) 1
log .log 2x
x x 2
2 2 22 log log logx x x
2
2
2
2
2
2
log 2
log 2 2
2log 2
x
x x
x x
Vậy nghiệm của phương trình là:2
2
2
2
x
x
b)3 9
2. log 3 log 3 log 3 0x x x
(1)
Điều kiện: 0 1x
Ta có: (1)3 3 3
2 1 30
log log 3 log 9x x x
2
3 3
4
33
1
23
6 log 11log 4 0
4log 3
31
log 32
x x
x x
x x
Vậy nghiệm của (1) là
4
3
1
2
3
3
x
x
.
2. Giải phương trình và b t phương trình
a)2 2 25
4 9 6
2
x x x x x x b)
3 2 2 3 2 2 6
x x
c) 3 5 3 5 3.2x x
x d) 2
2
2log ( ) log 32 6
x x x x
e) 2 3
4 16
2
log 40 log 14 logx x x
x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 125/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 125 -
Giải:
a)2 2 25
4 9 6
2
x x x x x x (1)
Ta có: (1)
2 2
2 3 5
3 2 2
x x x x
Đặt t =
2
2
3
x x
, t > 0.
(1) trở thành: 1 52t
t 22 5 2 0t t
2
2
2 1(1)1
3 222 2
2 (2)3
x x
x x
t
t
Giải (1): 2
2
3
1(1) log
2x x
2
3
2
3
11 1 4 log2
21
1 1 4 log2
2
x
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 126/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 126 -
Giải (2): 2
2
3
(2) log 2x x
2
3
2
3
1 1 4 log 2
21 1 4 log 2
2
x
x
Vậy phươnh trình có 4 nghiệm.
b) 3 2 2 3 2 2 6x x
(1)
Ta có: 3 2 2 =
1
3 2 2
Đặt t = 3 2 2x
, t > 0
Ta có: (1) trở thành:1
6t t
2 6 1 0t t
3 2 2 3 2 23 2 2 1
13 2 2 3 2 2 3 2 2
x
x
t x
x t
Vậy nghiệm của (1) là1
1
x
x
.
c) 3 5 3 5 3.2x x
x (1)
3 5 3 5 3.2x x
x 3 5 3 5
32 2
x x
Ta có:3 5 1
2 3 5
2
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 127/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 127 -
Đặt t =3 5
2
x
, t > 0 ; (1) trở thành1
3t t
2 3 1 0t t
3 5 3 53 5
2 22
3 5 3 5 3 52 2 2
1
1
x
x
t
t
x
x
Vậy nghiệm của phương trình là 11
x
x
d) 2
2
2log ( ) log 32 6
x x x x
(1)
Điều kiện:
2
2
( ; 0) (1; )0
1 512
x x x
x x x
Ta có: (1) 2
2 2
2
5log ( ) 6
log ( )x x
x x
2 2 2
2 2
2
2
22
2
log ( ) 6 log ( ) 0
1 log ( ) 5
2 02 3232 0
( ; 1] [2; )1 129 1 129
; 1 2;1 129 1 129; 2 2
2 2
x x x x
x x
x x x x x x
x
x x
Vậy ta có tập nghiệm của (1) là1 129 1 129
; 1 2;
2 2
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 128/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 128 -
e) 2 3
4 16
2
log 40 log 14 logx x x
x x x (1)
Điều kiện:1 1
0 ; ;1;216 4
x
Tacó :(1)2 3
2 2 2
2 22
log log log40 14
log 4 log 16log
2
x x x
x x x 2 2 2
2 2 2
2 log log log20 42
log 1 2 log 4 log
x x x
x x x
2
2 2
1
22
2
2 log 3 log 2 0
1log 2
2 4log 2
x x
x x
x x
Vậy nghiệm của phương trình (1) là
1
22
4
x
x
g) 2 2
1 2 1 3log (6 5 1) log (4 4 1) 2
x x x x x x
(1)
Điều kiện: 2
2
10 1 2 1
20 1 3 1 1 1
;6 5 1 0 3 3
1 14 4 1 0 ; ;3 2
x x
x x x
x x
x x x
Ta có: (1) 1 2
1 2
11 log (1 3 ) 2 2log (1 3 )x
x
x x
1 2
2
1 2
1 2 1 2 1 2
21 2
1 2 1 2
2
log (1 3 ) log (1 3 ) 2 0
1log (1 3 ) 1 log (1 3 ) log1 2
log (1 3 ) 2 log (1 3 ) log (1 2 )
1(1 3 ) ((1 2 ) 1) 0
1 2(1 3 ) (1 2 ) ((1 2 ) 1) 0
x x
x x x
x x x
x x
x x x
x x x
x x
x x x x
2
2
(6 5 )0
1 2(4 ) 0
x x x
x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 129/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 129 -
1 5 1 1; ; ;
2 6 4 4x x
Kết hợp với điều kiện ban đầu ta được tâp nghiệm của (1) là
1 1
;4 3x
.
Giải:
a)2 2sin cos2 2 3x x (1)
Ta có: (1)2
2
sin
sin
22 3
2
x
x
2 22 sin sin2 3.2 2 0x x
2
2
sin 2
2sin
2 1 sin 0
,sin 12 22
x
x
x k x
k Z x x k
Vậy nghiệm của phương trình là ,
2
x k
k Z x k
b)2 22 2(5 2 6) (5 2 6) 10x x x x (1)
Điều kiện: 2 2 0 ( ; 0) (2; )x x x
3 . Giải các phương trình và bất phương trình:
a)2 2sin cos2 2 3x x b)
2 22 2(5 2 6) (5 2 6) 10x x x x
c)2 1 3 2 2
log (cos 1) log (cos 2 3)x x
d)2 4
log 4 log 5 0x x
f) 2 1 2 2( 1)3 3 1 6.3 3x x x x h) 2(5 24) 5 7 5 7x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 130/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 130 -
Ta có: 5 2 61
5 2 6
Đặt2 2(5 2 6) x x t , t > 0.
(1) trở thành1
10t t
2
2
2
2
2
10 1 0
5 2 6 (5 2 6) 5 2 6
5 2 6 (5 2 6) 5 2 6( )
x x
x x
t t
t
t vn
2 2 1 0x x 1 2
1 2
x
x
Vậy nghiệm của phương trình là1 2
1 2
x
x
.
c)2 1 3 2 2
log (cos 1) log (cos 2 3)x x
(1)
Điều kiện:cosx 1 0
s2 3 0x
co x
Ta có: (1)1
2
2 1 2 1log (cos 1) log (cos 2 3)x x
1
2
2
cos 1 (cos2 3)
cos 2 cos 1 0
cos 1
2
x x
x x
x
x k
Kết hợp với điều kiện ban đầu ta được: x = 0
Vậy x = 0 là nghiệm của (1).
d)2 4
log 4 log 5 0x x (1)
Điều kiện: x 0
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 131/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 131 -
Ta có: (1)4 4
2 log 4 log 5 0x x
4
4
2 14log (*)
22 14log 0
2
x
x
4
18 4 14log 4x
18 4 14
18 4 14 4
418 4 14
4
44
4
x x
x
Vậy nghiệm của (1) là
18 4 14
4
18 4 14
4
4
4
x
x
f) 2 1 2 2( 1)3 3 1 6.3 3x x x x (1)
Điều kiện: 2( 1)1 6.3 3x x 0 x R
Ta có: (1)
2 2
3.3 9.3 (3.3 1)
x x x
2
2
3
3
3.3 9.3 3.3 1
3.3 12.3 1 0
6 2 63 log (6 2 6) 1
36 2 6 log (6 2 6) 1
33
x x x
x x
x
x
x
x
Vậy nghiệm của (1) là: 3
3
log (6 2 6) 1
log (6 2 6) 1
x
x
h) 2(5 24) 5 7 5 7x x x (1)
Điều kiện:5
log 7x
Ta có: (1) 2.5 48 5 7 2 2(5 24)(5 7) 5 7x x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 132/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 132 -
2
2.5 34 2 2(5 24)(5 7)
(2.5 ) 2500
2
x x x
x
x
Vậy x=2 là nghiệm của (1).
Giải:
+ 0a phương trình có nghiệm 0x
+ Ta có 1
2 21 1x a a a x
x x
1x a a x a
2 2 22 2 1x a a x a x a a 2 2 22 1a x a
2 2 4 24 4 2 1a x a a 2
2 24 1x a
+ 0, 1a a phương trình vô nghiệm
+ 1a phương trình có nghiệm 0x
Phương trình đối nghịch của mũ, loga:
Giải:
12) 3 1 2 (1)x
x a
Ta có:(1) 2 23 1 2.4
x x
4. Giải và biện luận phương trình:1
2 21 1x a a a x
x x
1. Giải các phương trình và b t phương trình:
12) 3 1 2
x
x a 3) ( 2)log 5c x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 133/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 133 -
+TH 1: 0, 4 3 0x 2 24 3x x
2 22.4 1 3x x
(1) vô nghiệm
+TH 2: 0x 2 21 3x x
2 22.4 1 3x x
(1) vô nghiệm
+TH 3: 0x không phải là nghiệm của (1)
Vậy phương trình (1) vô nghiệm
) log log 2 cos 0a x
b x a a : ĐK 1 0x
Đặt loga
x t . Ta có pt:1
2 cos 0t a t
2 2 cos 1
0t t a
t
Xét pt 2 2 cos 1 0t t a
2 2' cos 1 sin 0a a
Do đó 2 2 cos 1 0t t a t
+ TH1: 2 2 cos 1 0t t a
2' sin 0a a k
* 2 ( 0)a n n 1t 1
(1)x a
* (2 1) ( 0)a n n 1t (2)x a
+TH2:2 2 cos 1 0
0
t t a
t
0t log 0a
x
* 0 1a 1 (3)x
* 1a 0 1x (4)
Từ (1), (2), (3), (4)
0 1 : 1
1 : 0 1(2 1) ( 0)
a x
a x a n n
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 134/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 134 -
KL:
0 1 : 1
1 : 0 1
(2 1) ( 0)
a x
a x
a n n
3) ( 2)log 5 (1)c x x , ĐK: 0x
(1) 3
5log
2x
x
+ Nhận thấy (1) có nghiệm 3x
+ ta có3
( ) log f x x là một hàm đồng biến,5
( )
2
g x
x
là một hàm nghịch biến.Tức là ( ) f x
giao với ( )g x tại duy nhất một điểm
Vậy pt có duy nhất một nghiệm 3x
2 5 2log 3 log log 10) (1)
x d x x x x .
ĐK: 0x
+ Đặt2
logt x
(1) 2 3 5 10t t t t 1 3 1
15 10 2
t t t
(2)
Nhận thấy 1t là một nghiệm của (2)
+ Đặt1 3 1
( )5 10 2
t t t
f x
ta có1 1 3 3 1 1
'( ) ln ln ln 05 5 10 10 2 2
t t t
f t
( ) f t là hàm đồng biến, vế phải của (2) là một hàm hằng nên 1t là nghiệm duy nhất
Với 1t 2
log x =1 2x
Vậy nghiệm của phương trình là 2x
2. Giải các phương trình và b t phương trình
5log ( 3)) 2
x a x
) 3.9 (13 3 )3 4 0x x c x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 135/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 135 -
Giải:
5log ( 3 )
) 2 (1)x
a x
ĐK 3
0
x
x
0x
(1) 5 2
log ( 3) logx x . Đặt2
log x t
Ta có
2
5 3
t
t
x
x
5 2 3t t 2 1
1 3 (3)5 5
t t
Nhận thấy t = 1 là một nghiệm của (3)
Đặt2 1
( ) 35 5
t t
f t
'( ) 0 f t nên ( ) f t là hàm nghịch biến, vế tráicủa (3) là hàm hằng
nên (3) có nghiệm duy nhất t = 1
Với = 1 x = 2
Vậy nghiệm của phương trình là x = 2
2
2 3) log log ( 3 13) (1)b x x x
ĐK: 0x , 2 3 13 0x x
+ Đặt2
log x t (1) 2
2
3 3 13
t
t
x
x x
3 3.2 13 4t t t
3 1 1
3 13 1 (2)4 2 4
t t t
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 136/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 136 -
(2) nhận t = 3 là một nghiệm
+ Đặt3 1 1
( ) 3 134 2 4
t t t
f t
'( ) 0 f t ( ) f t là hà nghịch biến, vế phải của (2) là
một hàm hằng nên t = 3 là nghiệm duy nhất
Với t = 3 x = 8 (thoả đk)
Vậy nghiệm của phương trình là x= 8
) 3.9 (13 3 )3 4 0x x c x x
Đặt 3x t pt tương đương 23 (13 3 ) 4 0t x t x
2(3 11)x
1
34
t
t x
+1
3t 13 3x 1x
+ 4t x 3 4 (1)x x Đặt ( ) 3x f x x là hàm đồng biến ( '( ) 0 f x )
Nên (2) có nghiệm duy nhất x = 1
Vậy nghiệm của phương trình là 1x
2 2
5 5) ( ) log (11 5)log 30 0 (1)d x x x x x ĐK: 0x
Đặt 5log x t .(1)
2 2
( ) (11 5) 30 0x x t x t 5x 2 2121 110 25 120 120x x x x = 2( 5)x
6
15
t x
t x
+ 5t x
5 5log x x
5x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 137/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 137 -
+6
1t
x
5
6log
1x
x
Vậy nghiệm của phương trình là 5x
Giải:
2
2
2 3 2) log 3 log (4 2 )
x x a x x
ĐK:2
2
1 3 2 0
4 2 0
x x x
x x
+ Ta có 2 22 2 (1 )log 3 log (3 (1 ) )x x (1)
+ Đặt 2(1 )t x 2 2
log 3 log (3 )t
t
t=0 là 1 nghiệm, mà VT là hàm hằng, vế phải là hàm đồng biến nên t=0 là nghiệm duy nhất
2(1 )x =0 x=1
Vậy nghiệm của phương trình là x = 1
2 2
2 3) log ( 3 2 1) log ( 3 4) 0 (1)b x x x x
ĐK: ; 2 1;x
Đặt 2 3 2t x x (1) 2
2 3log ( 1) log ( 2) 0 (*)t t
(*) nhận t=1 làm nghiệm mà VT (*) đồng biến, vế phải là hàm hắng t=1 là nghiệm duy nhất
3. Giải các phương trình và b t phương trình
2
2
2 3 2
2 2
2 3
) log 3 log (4 2 )
) log ( 3 2 1) log ( 3 4) 0
x x a x x
b x x x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 138/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 138 -
t = 1 2 3 2 1x x
3 5
23 5
2
x
x
(thoả)
Vậy nghiệm của phương trình là3 5
2x
,
3 5
2x
Hệ mũ, loga:
Giải:
Điều kiện:0
y x
y
Hpt 4 4
2 22 2
log 1 log ( )4
25 25
y y y x y x
x y x y
2 22
33 4 04
25 25 400
y x x y
x y y
3
4
x
y
Vậy hệ có nghiệm là (3;4).
Giải:
(2004-A) Giải hệ phương trình:1 4
42 2
1log ( ) log 1
25
y x y
x y
(2002-D)Giải hệ phương trình:
3 2
1
2 5 4
4 2
2 2
x
x x
x
y y
y
(1)
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 139/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 139 -
Ta có:14 2
22 2
x x x
x y y
Ta có: (1)3 25 4 0
2x
y y y
y
2 0
10
1 2
4 4
x y x
y y
y x
y y
Vậy nghiệm của (1) là: (0;1) v (2;4).
Giải:
Điều kiện:1
0 2
x
y
Hpt3 3
3 3
1 2 2 ( 1)(2 ) 1
log (3 ) log 3
x y x y
x y
3
3 33
2 ( 1)(2 )
(3 )log log 27
x y y x
x
y
2 2 2 8 4 8 0
y x
x y xy x y
y x
1
2
x y
x y
Vậy nghiệm của (1) là (1;1) v (2;2).
BÀI TẬP TƯƠNG TỰ:
(2005-B) Giải hệ phương trình:2 3
9 3
1 2 1
3 log (3 ) log 3
x y
x y
(1)
b)
lg lg
lg 4 lg 3
3 4
4 3
x y
x y
d)
2 2
2 3
1
log log 1
x y
x y x y
e) 2 2
1 1log 1 2 log 1 2 4
x y y y x x
g)
log 1xy
x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 140/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 140 -
Giải:
b)
lg lg
lg 4 lg 3
3 4
4 3
x y
x y
,
ĐK: 0, 0x y
Ta có
lg lg
lg 4 lg 3
3 4
4 3
x y
x y
2 2
lg 3 lg lg 4 lg
lg 4 lg 4 lg lg 3 lg 3 lg
x y
x y
2
2 3 2
lg 4 lg 3 lg lg 4 lg
lg 3 lg 4 lg 3 lg 4 lg lg 3 lg 3 lg
x y
x y
2 2 3 2lg 3 lg 4 lg 4 lg lg 3 lg 3 lgy y
2 2 2 2lg lg 4 lg 3 lg 3 lg 4 lg 3 0y 2 2lg 4 lg 3 lg lg 3 0y
lg lg 3y 1
3y
1
4x
Vậy nghiệm của hệ phương trình là1 1
;4 3
d)
2 2
2 3
1
log log 1
x y
x y x y
,
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 141/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 141 -
ĐK: 0, 0x y x y
Ta có
2 2
2 3
1
log log 1
x y
x y x y
2 3
1
1
log log 1
x y x y
x y x y
2 3log log 1x y x y
3
3
3
loglog 1
log 2
x y x y
3
3
1log 1 1
log 2x y
3
3
3
log 2log
1 log 2x y
3
3
3
3
log 2
1 log 2
log 2
1 log 2
3
3
x y
x y
3 3
3 3
log 2 log 2
1 log 2 1 log 23 3
2x
;
3 3
3 3
log 2 log 2
1 log 2 1 log 23 3
2y
Vậy nghiệm của hệ phương trình là
3 3 3 3
3 3 3 3
log 2 log 2 log 2 log 2
1 log 2 1 log 2 1 log 2 1 log 23 3 3 3
;2 2
e)
2 2
1 1
1 1
log 1 2 log 1 2 4
log 1 2 log 1 2 2
x y
x y
y y x x
y x
(*)
Giải:
ĐK
0 1 1
10 1 12
1 2 0 11
21 2 0
x
x y
y y
x
(*)
1 1
1 1
log 1 log 1 2 1
log 1 2 log 1 2 2 2x y
x y
y x
y x
Ta có: (1) 2
1 1log 1 2 log 1 1 0x x y y 1log 1 1x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 142/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 142 -
1 1y x
y x
thế vào (2) ta được
1 1log 1 2 log 1 2 2
x x x x
22
1 1log 1 4 log 1
x x x x
2
21 4 1x x 25 2 0x x
0 (l )
2
5
x oai
x
2
5x
2
5y
Vậy nghiệm của hệ phương trình là2
5x ,
2
5y
g)
5
log 1
2 log log
xy
x y
x y
xy xy
(*) ,
Đk:1,
0, 0 1
xy x y
xy x y
Giải:
Ta có: (*) 1 1
2 log 5 log ( )xy xy
xy x y
x y
2 log 5 log ( )
xy xy
xy x y
x y
25
xy x y
x y
(25 ) 25x x x x 225 2 25x x x , đk x 252
2 2(25 2 25)(25 2 25) 0x x x x x x 2 2(23 25)(27 25)x x x x =0
2
2
23 25 0 (1)
27 25 0 (2)
x x
x x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 143/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 143 -
(1)
23 629(l )
223 629 27 629
2 2
x oai
x y
(2) 27 629 23 629
2 2x y
(loại vì x<y)
Vậy nghiệm của hệ phương trình là23 629 27 629
;2 2
x y
h)
219 9 (1)
3 3 24 (2)
x y y
x y x
x y
Giải:
Điều kiện: x0, y Z
(1)1 21
2 2 229 .9 9 9 9 2 .x y x
y y y y y x
(2)2 3 4 2 1
4 4 v y=2 2
y y y y
y y
Vậy hệ có nghiệm là: x = -2, y = 4.
b*)
22
2 3 log 3 4
2
2 3 (1)
4 1 3 8 (2)
x x y
y y y
Giải:2
22 3 log 3 4(1) 2 3
x x y
* Với y1
Ta có (2) 24 1 ( 3) 8y y y 2 9 2 0y y vô nghiệm vì VT >0
* Với 0y1:
(2)
2
4 1 ( 3) 8y y y
2
11 0y y
11 0y
suy ra y=0
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 144/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 144 -
* Với y 0:
(2) 24 1 ( 3) 8y y y 2 3 0y y 3 0y 3 0y
33 1y Mặt khác 2 2 3 0x x 2 2 3
2 1x x
. Từ đó ta có hệ
2
3
2 3
3 1
2 1
y
x x
2
3 0
2 3 0
y
x x
1
3
x
y
hoặc3
3
x
y
Vậy nghiệm của hệ phương trình là ( 1; 3);(3; 3)
c*)
1 2 1
4
4 3.4 1 (1)
3 2 log 2 (2)
x y y
x y
Giải: Ta có (2) 4log 23 2 14 4
2x y Áp dụng bất đẳng thức Cauchy ta có:
(2) 1 2 1 3 2 12 4 3.4 2 3.4 2 3 2
2x y y x y (vô lí)
Vậy hệ phương trình vô nghiệm
16. Giải các hệ phương trình
a)
123
x y y x
x y x y
b)
1
3 3
12 8
x x y y
x y y
c)2 2
14
84
x y xy
x y xy
d) 2 23 3
3 3
2 3
6
x y x y y x
x y
e)3 3 65
210
x y xy
x y
f)
lg lg
lg 4 lg 33 4
4 3
x y
x y
g)
2 2
2 3
1
log log 1
x y
x y x y
h) 3 3
2 2
3 3 1
1
y x x y xy
x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 145/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 145 -
Giải:
a)
1(1)
2
3 (2)
x y y x
x y x y
ĐK: 0, 0x y + 0x y là 1 nghiệm của hệ
+ , 0x y (1):(2)6
x y x
x y y
2 26 6xy y x xy 2 26 5 0x y xy
2
5 6 0x x
y y
2 (3)
3 (4)
x
y
x y
(3) 2x y 3 2 3y y y 1
2
y 2x
(4) 3x y 4 3 3y y y 3
4y
3 3
4x
Vậy nghiệm của hệ phương trình là1
2;2
,
3 3 3;
4 4
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 146/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 146 -
b)
13 3
12 8
x x y y
x y y
+ Ta có
13 3
12 8
x x y y
x y y
13 3
13 5
x x y y
x x y y
+ Đặt1
0u x y
, 3 0v x y 2 2
3
5
u v
u v
2
2 3 5u u
2 29 6 5u u u 22 6 4 0u u 2 3 2 0u u 1 2 (1)
2 1 (2)
u v
u v
(1)
11
3 2
x y
x y
11
7
x y
x y
17 1
7
y y
x y
4 10
3 10
x
y
,4 10
3 10
x
y
(2)
1 2
3 1
x y
x y
1 4
4
x y
x y
14 4
4
y y
x y
5 10
23 10
2
x
y
,3 10
25 10
2
x
y
Vậy nghiệm của hệ pt là4 10
3 10
x
y
;4 10
3 10
x
y
;
5 10
23 10
2
x
y
;
3 10
25 10
2
x
y
c)2 2
14
84
x y xy
x y xy
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 147/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 147 -
Ta có2 2
14
84
x y xy
x y xy
2
2
196 28
84
xy x y x y
x y xy
2 2
84 196 28x y x y x y 28 280x y 10x y 10
16
x y
xy
2
8
x
y
;8
2
x
y
d) 2 23 3
3 3
2 3
6
x y x y y x
x y
Ta có 2 23 3
3 3
2 3
6
x y x y y x
x y
33 3
3 3
2 3
6
x y xy x y
x y
Mà 3
3 33 6x y 2 23 33 216x y x y y x 3 216x y 72x y
3
144 18 xy 512xy
8
64
x
y
,
8
64
y
x
Vậy nghiệm của hệ phương trình là 8;64 , 64;8
e)3 3 65
210
x y xy
x y
Ta có 33 2 233 3 10x y x xy y
236 3 35 3 102
xy x y xy
2
6 6 35 5
3 102 2
xy xy xy
6 35 13
. 102 4
xy xy
256
169xy
2
13128
13
x
y
;
2
13128
13
y
x
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 148/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 148 -
Vậy nghiệm của hệ phương trình là2 128 128 2
; , ;13 13 13 13
f)
lg lg
lg 4 lg 3
3 4
4 3
x y
x y
,
ĐK: 0, 0x y
Ta có
lg lg
lg 4 lg 3
3 4
4 3
x y
x y
2 2
lg 3 lg lg 4 lg
lg 4 lg 4 lg lg 3 lg 3 lg
x y
x y
2
2 3 2
lg 4 lg 3 lg lg 4 lg
lg 3 lg 4 lg 3 lg 4 lg lg 3 lg 3 lg
x y
x y
2 2 3 2lg 3 lg 4 lg 4 lg lg 3 lg 3 lgy y
2 2 2 2lg lg 4 lg 3 lg 3 lg 4 lg 3 0y 2 2lg 4 lg 3 lg lg 3 0y lg lg 3y
1
3y
1
4x
Vậy nghiệm của hệ phương trình là1 1
;4 3
g)
2 2
2 3
1
log log 1
x y
x y x y
ĐK: 0, 0x y x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 149/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 149 -
Ta có
2 2
2 3
1
log log 1
x y
x y x y
2 3
1
1log log 1
x y x y
x y x y
2 3log log 1x y x y 3
3
3
log log 1log 2
x y x y
3
3
1log 1 1
log 2x y
3
3
3
log 2log
1 log 2x y
3
3
3
3
log 2
1 log 2
log 2
1 log 2
3
3
x y
x y
3 3
3 3
log 2 log 2
1 log 2 1 log 23 32
x
;
3 3
3 3
log 2 log 2
1 log 2 1 log 23 32
y
Vậy nghiệm của hệ phương trình là
3 3 3 3
3 3 3 3
log 2 log 2 log 2 log 2
1 log 2 1 log 2 1 log 2 1 log 23 3 3 3
;2 2
h)
3 3
2 2
3 3 1
1
y x x y xy
x y
Ta có 3 3
2 2
3 3 1
1
y x x y xy
x y
3 3
2 2
3 3 1
1
y x x y xy
x y
2 2
1 3 3 1
1
y x x y xy xy
x y
2 2
1
3 3
1
y x
xy
x y
x y
2 2
2 2
1(1)
1
3 3
(2)1
y x
xy
x y
x y
x y
(1) 2
2 1x y Vô nghiệm
(2)2 2
3 3;
1
y x y x
x y
Đặt ( ) 3t f t t ; ( ) f t đồng biến nên: ( ) ( )x y f x f y . Do đó x =
y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 150/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 150 -
2 2 1
x y
x y
1
21
2
x
y
;
1
21
2
x
y
Vậy nghiệm của hệ phương trình là1 1 1 1
; , ;2 2 2 2
k)
2 2
1 1
1 1
log 1 2 log 1 2 4
log 1 2 log 1 2 2
x y
x y
y y x x
y x
(*)
Giải:
ĐK
0 1 11
0 1 12
1 2 0 11
21 2 0
x
x y
y y
x
(*) 1 1
1 1
log 1 log 1 2 1log 1 2 log 1 2 2 2
x y
x y
y x y x
(1) 2
1 1log 1 2 log 1 1 0
x x y y
1
log 1 1x
y
1 1y x
y x thế vào (2) ta được
1 1log 1 2 log 1 2 2
x x x x
22
1 1log 1 4 log 1
x x x x
2
21 4 1x x 25 2 0x x 0 (l )
2
5
x oai
x
2
5x
2
5y
Vậy nghiệm của hệ phương trình là2
5x ,
2
5y
1)
5
log 1
2 log log
xy
x y
x y
xy xy
(*) , Đk:1,
0, 0 1
xy x y
xy x y
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 151/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 _ ĐH Tây Nguyên - 151 -
Giải : (*) 1 1
2 log 5 log ( )xy xy
xy x y
x y
2 log 5 log ( )
xy xy
xy x y
x y
25
xy x y
x y
(25 ) 25x x x x 225 2 25x x x , đk x25
2
2 2(25 2 25)(25 2 25) 0x x x x x x 2 2(23 25)(27 25)x x x x =0
2
2
23 25 0 (1)
27 25 0 (2)
x x
x x
(1)
23 629
223 629 27 629
2 2
x
x y
(2) 27 629 23 629
2 2x y
(loại vì x<y)
Vậy nghiệm của hệ phương trình là 23 629 27 629;2 2
x y
n)
22
2 3 log 3 4
2
2 3 (1)
4 1 3 8 (2)
x x y
y y y
Giải:2
22 3 log 3 4(1) 2 3
x x y
* Với y1 ta có (2) 24 1 ( 3) 8y y y 2 9 2 0y y vô nghiệm vì VT >0
* Với 0y1:(2) 24 1 ( 3) 8y y y 2 11 0y y 11 0y
suy ra 0y
* Với y 0:(2) 24 1 ( 3) 8y y y 2 3 0y y 3 0y
3 0y
loại
5/13/2018 ĐA ̣I SÔ ́ SƠ CÂ ́P_ÔN THI ĐA ̣I HO ̣C - slidepdf.com
http://slidepdf.com/reader/full/dai-so-so-capon-thi-dai-hoc 152/152
Lê Ngọc Sơn_Hồ Quan Bằng_Nguyễn Xuân Tuần_Nguyễn Quốc Việt
Lớp Sư Phạm Toán K07 ĐH Tây Nguyên 152
33 1y Mặt khác 2 2 3 0x x 2 2 3
2 1x x
Từ đó ta có hệ
2
3
2 3
3 1
2 1
y
x x
2
3 0
2 3 0
y
x x
1
3
x
y
hoặc3
3
x
y
Vậy nghiệm của hệ phương trình là ( 1; 3);(3; 3)
p)1 2 1
4
4 3.4 2 (1)
3 2 log 2 (2)
x y y
x y
Giải: Ta có (2) 4log 23 2 14 4
2x y
(2) 1 2 1 3 2 12 4 3.4 2 3.4 2 3. 2
2x y y x y (vô lí)
Vậy hệ phương trình vô nghiệm

































































































































































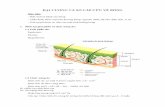





![Tạp chí con đường đại học số 2 [ trường học số ]](https://static.fdocuments.net/doc/165x107/54931f8bb47959794d8b4795/tap-chi-con-duong-dai-hoc-so-2-truong-hoc-so-.jpg)



