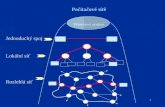
Petriho sítě a GRAFCET, Hanzálek, CAK 2001
Transcript of Petriho sítě a GRAFCET, Hanzálek, CAK 2001

1
�
1. Petr iho sí tě a Grafcet
1.1. Petriho sítě Petriho sítě jsou grafický a matematický nástroj vhodný pro modelování a analýzu systémů diskrétních událostí. Komunikací s automaty se zabýval německý matematik C.A. Petri a ve své disertační práci (1960-62) definoval formalismus později nazvaný Petriho sítě. Tento formalismus byl rozpra-cován na začátku sedmdesátých let na MIT (Massachusetts Institute of Technology) a od po-čátku osmdesátých let se každoročně koná mezinárodní konference zaměřená na teorii a apli-kace Petriho sítí. Díky své schopnosti jednoduše modelovat systémy diskrétních událostí obsahující paralelis-mus, sdílení zdrojů, vazbu na reálný čas a vazbu na okolní prostředí, se Petriho sítě staly oblí-beným nástrojem teoretiků i praktiků. Zejména teoretické výsledky z této oblasti jsou zajíma-vé, jelikož umožňují formálně prokázat vlastnosti modelovaných systémů. Petriho sítě lze zdárně aplikovat v různých oblastech informatiky a automatizace. Zvláště je-jich schopnost modulárně reprezentovat paralelně běžící procesy a komunikace je výrazně odlišuje od stavového diagramu.
1.1.1. Základní názvosloví Neoznačená Petriho síť je orientovaný ohodnocený bipartitní graf. Jako každý graf se i Petri-ho síť skládá z uzlů, jež jsou propojeny hranami. Přívlastek orientovaný značí skutečnost, že hrany grafu jsou orientované. Přívlastek ohodnocený značí skutečnost, že hranám mohou být přiřazeny váhy. Přívlastek bipartitní značí skutečnost, že množina uzlů grafu se skládá ze dvou disjunktních podmnožin – množiny míst a množiny přechodů, přičemž místa a přechody se v průběhu cesty střídají. Označená Petriho síť vznikne umístěním značek do míst neoznačené Petriho sítě.
� místo – může obsahovat nezáporný celý počet značek � přechod – v okamžiku jeho aktivace (přeskoku) jsou ode-
brány značky ze vstupních míst a přidány značky do vý-stupních míst přechodu
� orientované hrany - propojují místa a přechody � počáteční značení (umístění značek v místech před prvním
přeskokem) popisuje počáteční stav systému � vývoj systému je reprezentován přesunem značek v síti na
základě aktivace (přeskoku) přechodů � každé nové značení reprezentuje nový stav systému
Poznámka pro hloubavé: Bylo by zásadní chybou hledat podobnost mezi topologií Petriho sítě a topologií stavového digramu, jež je také orientovaným grafem (jednotlivé stavy jsou uzly tohoto grafu). Pro pře-hlednost uveďme následující důležitá tvrzení: � graf reprezentující všechna dosažitelná značení v Petriho síti je ekvivalentní stavovému
diagramu (praktický dosah tohoto tvrzení uvidíme v níže uvedených příkladech)
hrana
místo se značkou
hrana
přechodhrana
místo bez značky

2
� čtenáři dobře známý stavový diagram lze také nakreslit jako Petriho síť s totožnou topolo-gií. Tato Petriho síť v sobě bude mít během vývoje systému právě jednu značku (ta se bude nacházet v místě jež odpovídá aktivnímu stavu), takže nebude schopna reprezentovat para-lelismus a pozbude tak veškeré elegance.
1.1.2. Pravidla pro změnu stavu systému Jelikož každý přechod může mít jedno nebo více vstupních a výstupních míst, je potřeba defi-novat, za jakých podmínek dochází k přesunu značek v síti, neboli za jakých podmínek dochá-zí k aktivaci přechodů. Přechod je uvolněn, jestliže každé jeho vstupní místo obsahuje počet značek > váze hrany spojující vstupní místo a přechod. Uvolnění přechodu je nezbytnou (nikoli postačující podmínkou) pro jeho aktivaci (přeskoče-ní). Pro aktivaci přechodu musí být splněny další podmínky v závislosti na typu Petriho sítě (například výskyt události asociované s přechodem u synchronizovaných Petriho sítí nebo blíže neurčený okamžik u autonomních Petriho sítí) a “uvolňující“ značky nesmí být spotře-bovány jiným přechodem (). Při aktivaci jsou odebrány značky ze vstupních míst a nové značky jsou vloženy do výstupních míst. Počet odebraných/vložených značek odpovídá váze vstupní/výstupní hrany. Aktivace je nedělitelná operace. Pro jednoduchost si můžeme představit, že doba aktivace je rovna nule. Příklady aktivace autonomní Petriho sítě (autonomní = její vývoj je nezávislý na okolním pro-středí) vidíme na následujícím obrázku, kde čísla připsaná k hranám reprezentují jejich váhu (v případě, kdy je váha hrany rovna 1 se číslo nepíše):
Příklady aktivace Petriho sítě
Důvod, proč jsme zvlášť definovali uvolnění a zvlášť aktivaci přechodu vidíme názorně z následujícího obrázku, kde jsou oba přechody T1 a T2 uvolněny, ale pouze jeden z nich je aktivován. Tato situace se nazývá efektivní konflikt a je nutno předeslat, že úlohou Petriho sítě je konflikt modelovat, nikoli však řešit (například pomocí priority přechodů). Neboli uvedený systém se může vyvíjet dvěma způsoby – do stavu S1 nebo do stavu S2.
karoserie kola motor
automobil
oběd hladový úředník
špinavé nádobí sytý úředník výlisek odpad
tabule plechu
4
3
3
Tento přechod nemůže býtaktivován, jelikož k výroběautomobilu jsou nezbytnáčtyři kola (pokud to ovšemnení Velorex).
AkivaceAkivace
P1 P2
P1 P2
P3 P4
P3 P4
P6 P7
P6 P7
P5
P5
P8 P9 P10
P11
T3 T2
T1
T1 T2

3
Příklad efektivního konfliktu mezi přechody T1 a T2
Z výše uvedených pravidel pro aktivaci přechodu lze odvodit některé typické konstrukce, s kterými se setkáme při modelování systémů pomocí Petriho sítí: paralelismus (přechod s více výstupními hranami) – konstrukce při níž z jedné sekvence vznikne více souběžně vykonávaných a na sobě nezávislých sekvencí (např. založení procesu v operačním systému) synchronizace (přechod s více vstupními hranami) – konstrukce při níž několik sekvencí na sebe navzájem čeká a poté pokračuje jedinou sekvencí (např. schůzka dvou partnerů) výběr (místo s více výstupními hranami) – konstrukce, jež umožňuje, aby se značka pohybova-la různými cestami (např. instrukce switch v jazyku C, nebo sdílení zdrojů) spojení (místo s více vstupními hranami) – konstrukce, jež spojuje několik možných cest vývoje systému do jediné (ukončení instrukce switch v jazyku C, nebo vrácení sdíleného zdroje)
1.1.3. Příklady modelování synchronizovanou Petriho sí-tí
Příklad 1: V počátečním stavu systému se vozík T nachází na kontaktu a. Po stlačení tlačítka s se pohybuje doprava R. Po dosažení kontaktu b se vozík vrací na kontakt a pohybem vlevo L L R
◄──┴──►┌───────┐ ┌─┐│ T │ ─┴─┴─
│└o─────o┘ │ ──o o──a └──────────────────────────────┘b s
Při modelování synchonizovanou Petriho sítí ( syn-chronizovaná = aktivace přechodu je vázána na výskyt události) jsme navíc k jednotlivým místům připojili akce (výstupy řídicího systému) které systém vykonává – čekání „wait“, pohyb vpravo „R“, pohyb vlevo „L“. Skutečnost, že všechna dosažitelná značení v Petriho síti odpovídají stavům ve stavovém diagramu je zřejmá z tabulky:
Stav Značení Petriho sítě (P1,P2,P3) S0 (1,0,0) S1 (0,1,0)
R
wait
L
wait
s.a
R
b
L
a
b
a
P1
T1
P2
T2
P3
T3
s.a
S0
S1
S2
Model Periho sítí Model stavovým diagramem
P4 P5 P6
T1 T2
P1 P2 P3
T1
M0=(1,1,1,0,0,0)
T2
hladový strávník A oběd hladový strávník B
S0
S1 S2
Stavovým diagramem seznačením (P1,P2,P3,P4,P5,P6)
sytý strávník A špinavé nádobí sytý strávník B
P4 P5 P6
T1 T2
P1 P2 P3
P4 P5 P6
T1 T2
P1 P2 P3
M1=(0,0,1,1,1,0) M2=(1,0,0,0,1,1)

4
S2 (0,0,1) Jelikož je tento systém velice jednoduchý, tak stavový diagram má totožnou topologii Petriho sítí.
Příklad 2: Po sepnutí tlačítka s se začnou vozíky T1 a T2 pohybovat z kontaktů a1, a2 dopra-va. Dosáhne-li některý z vozíků kontaktu b, zastaví se a čeká na druhý vozík. Po setkání v bodech b, se oba vozíky vrací do bodů a1, a2.
L1 R1 L2 R2 ┌─┐◄──┴──► ◄──┴──► ─┴─┴─
┌───────┐ ┌───────┐ ──o o──│ T1 │ │ T2 │ s└o─────o┘ └o─────o┘
a1└────────────────────────┘b1 a2└─────────────────────────┘b2
Tato paralelní evoluce dvou procesů (dvou vozíků) se dvěma synchronizačními body (přecho-dy T1 a T4) je dobře patrná z Petriho sítě. Lze říci, že topologie modelovaného systému (dva elementy s vlastní aktivitou) odpovídá topologii Petriho sítě (dvě paralelní větve). Na druhou stranu stavový diagram nereflektuje topologii modelovaného systému. O tom, že práce s Petriho sítí je značně pružnější než práce se stavovým diagramem, se zvídavý čtenář pře-svědčí v okamžiku, kdy se pokusí modelovat systém skládající se ze tří vozíků. V případě Pet-riho sítě stačí přidat třetí paralelní větev, ale stavový diagram je nutno celý překreslit. Příklad 3: Obdobně jako v příkladu 2 se po sepnutí tlačítka s začnou vozíky T1 a T2 pohybo-vat z kontaktů a1, a2 doprava. Dosáhne-li některý z vozíků kontaktu b, nečeká na druhý vozík a vrací do bodu a. V případě, kdybychom modelovali n vozíků synchronizovaných tlačítkem s, potom by Petriho síť obsahovala 3.n míst, zatímco stavový diagram by obsahoval 3 n stavů. Jelikož jak známo z příkladu 1 nachází se každý vozík ve 3 možných stavech (odhlédneme-li od ostatních vozíků) – čekání na startu, pohyb vpravo, pohyb vlevo.
a2a1
b1b2
b2b1
L2
R1 R2
P5
s.a1.a2
P6
T3
P7
P8
T6
wait
R2
b2
wait
L2
a2
R1,R2
L1,L2
wait
T1
R1
b1
wait
T4
L1
a1
a2
P1
P2
T2
P3
P4
T5
s.a1.a2
S1
Model Periho sítí Model stavovým diagramem
S2
S4
S3
a1
S5 L1S6
wait
S0

5
Příklad 4: Vozík T1 je ručně nakládán a po sepnutí tlačítka s1 se začne pohybovat z kontaktu a1 ve směru R1 až do kontaktu b1, kde je vyložen jeřábem. Po vyložení se vrací zpět ve směru L1 na kontakt a1. Stejně funguje i vozík T2, který se po sepnutí tlačítka s2 začne pohybovat z kontaktu a2 ve směru R2 až do kontaktu b2, kde je vyložen stejným jeřábem jako vozík T1. Jeřáb je tedy sdílen oběma vozíky – konec vykládky vozíku T1 ohlašuje signál k1, konec vy-kládky vozíku T2 ohlašuje signál k2.
┌─┐ ╞═══════════╤════════════╡k1,k2 ┌─┐─┴─┴─ │ ─┴─┴─
──o o── │ ──o o──s1 │ s2
L1 R1 ┌┴┐ R2 L2◄──┴──► │ │ ◄──┴──►
┌───────┐ ┌───────┐│ T1 │ │ T2 │└o─────o┘ └o─────o┘
a1└────────────────────────┘b1 b2└─────────────────────────┘a2
R1 R2
a2a1
b1b2
b2b1
L2
R1,L2 L1,R2
P4
s.a1.a2
P5
T3
P6
T5
wait
R2
b2
L2
a2
R1,R2
L1,L2
wait
T1
R1
b1
L1
a1
a2
P1
P2
T2
P3
T4
s.a1.a2
S1
Model Periho sítí Model stavovým diagramem
S2
S4
S3
a1
S5 L1S6
wait
S0
S8S7
a1 a2
b2 b1
P6
T6
P7
T7
P8
T8
P9
T9
P10
T10
P11
jeřáb volný
nakládka
s1.a1
R1
b1
wait
vykládka
k1
L1
a1
P1
T1
P2
T2
P3
T3
P4
T4
P5
T5
nakládka
s2.a2
R2
b2
wait
vykládka
k2
L2
a2

6
1.1.4. Formální definice autonomních Petriho sítí
Tato kapitola ukazuje, že Petriho sítě nejsou pouze grafický, ale i matematický nástroj.
D.1. Neoznačená Petriho síť R představuje uspořádanou čtveřici R = (P,T,Pre,Post), kde:
P = {Pi,...Pm} je konečná množina míst a |P|=m
T = {Ti,...Tn} je konečná množina přechodů a |T|=n
Pre : matice |P| x |T| obsahující celá nezáporná čísla reprezentující váhy hran jdoucích z míst do přechodů (precondition) Post: matice |P| x |T| obsahující celá nezáporná čísla reprezentující váhy hran jdoucích z přechodů do míst (postcondition)
D.2. Incidenční matice C je matice s m řádky a n sloupci pro kterou platí vztah C = Post - Pre D.3. Značená Petriho síť je dvojice (R,M). Kde M, značení Petriho sítě, je zobrazení z P do
celých nezáporných čísel takové, že M(Pi) je počet značek v místě Pi. Jelikož |P| = m, tak M(P) je sloupcový vektor s m prvky. M0 je počáteční značení Petriho sítě.
┌ T1 T2 T3┐
P1 │ 0 0 1 │Post = P2 │ 1 0 0 │ přechod -> místo
P3 │ 0 1 0 │└ ┘┌ T1 T2 T3┐
P1 │ 1 0 0 │Pre = P2 │ 0 1 0 │ místo -> přechod
P3 │ 0 0 1 │└ ┘┌ T1 T2 T3┐ ┌ ┐
P1 │-1 0 1 │ P1│ 1 │C = P2 │ 1 -1 0 │ Mo = P2│ 0 │
P3 │ 0 1 -1 │ P3│ 0 │└ ┘ └ ┘
D.4. Aktivace přechodu. Přechod Ti je uvolněn pro značení M jestliže ∀ Pj ∈ P; M(Pj) >
Pre(Pj,Ti). Neboli počet značek ve vstupním místě musí být > váze hrany jdoucí z tohoto místa do přechodu.
Jelikož chování autonomních Petriho sítí není vztaženo k okolnímu prostředí, tedy ani k času, nemůžeme určit, kdy je přechod aktivován (přeskočen). Toto je důležité zjištění zejména pro studium vlastností autonomních Petriho sítí, kdy bereme v úvahy všechny možné okamžiky kdy je přechod aktivován. Přitom pro autonomní Petriho síť platí, že uvolnění přechodu je jedinou podmínkou pro to, aby mohl být aktivován. Aktivací přechodu Ti se změní původní značení sítě M na nové značení M’ tak, že
∀∀∀∀ Pj ∈∈∈∈ P; M’(Pj) = M(Pj) - Pre(Pj,Ti) + Post(Pj,Ti)
D.5. Aktivační sekvence S je sekvence přechodů, jež byly uvolněny a přeskočeny v průběhu
vývoje systému. T1 T2 T4 T3 T5 T1
Př.: Pro vývoj systému M1 -> M2 -> M3 -> M4 -> M5 -> M6 -> M7
P1
T1
P2
T2
P3
T3

7
je aktivační sekvence S = T1T2T4T3T5T1
neboli říkáme, že aktivační sekvence S vede na změnu značení z M1 na M7 a píšeme:
M1 S >>>> M7
D.6. Charakteristický vektor je řádkový vektor s udávající kolikrát se daný přechod objeví v
průběhu aktivační sekvence S.
Př.: síť obsahuje přechody T1 ....T8 a aktivační sekvence S = T1T2T4T3T5T1 potom je charakteristický vektor s = (2 1 1 1 1 0 0 0)
D.7. Stavová rovnice Petriho sítě. Vývoj Petriho sítě ze značení M0 do M je popsán rovnicí:
M = M0 + C . s’
1.1.5. Vlastnosti Petriho sítí
Formální analýza systému je důležitou součástí každé kritické aplikace. Umožňuje prokázat funkčnost a bezchybnost systému ještě před jeho praktickou realizací. Petriho sítě jsou vhodným nástrojem pro analýzu systémů diskrétních událostí. Neboli poté co sytém namodelujeme (vytvoříme jeho grafickou reprezentaci a z ní odvodíme strukturu systé-mu a jeho značení ) máme možnost prokázat, jaké má systém vlastnosti – například, zda se nedostane do deadlocku (stavu, ve kterém zůstane zablokován). V následujícím textu uvedeme některé vlastnosti značených Petriho sítí.
Ohraničená Petriho síť Značená Petriho síť (R, M0) je ohraničená tehdy, jestliže pro libovolné dosažitelné značení M platí: ∀ Pi ∈ P; M(Pi) < k , kde k je celé kladné číslo.
Důsledek: Jestliže síť není ohraničená � počet značek v některém z jeho míst roste nade všechny meze � stavový diagram roste nade všechny meze � systém nelze realizovat konečným automatem.
Příklad ohraničené a neohraničené Petriho sítě
P1
T1
P2
T2
P5 P3
T3
P4
T4
P6
P1
T1
P2
T2
P3
T3
Místa P1, P2, P3, P4 jsou ohraničená pro k = 1Místa P5, P6 jsou ohraničená pro k = 3� Síť je ohraničená
Při n opakováních aktivační sekvenceS = T1T2 bude M’ = (1, 0, n)� Místo P3 není ohraničené� Síť není ohraničenáObdobně lze postupovat i pro P1 a P2sekvencemi T1T2T3 a T1 T3

8
Binární (bezpečné) Petriho sítě Každé místo obsahuje v průběhu vývoje systému nejvýše jednu značku. Neboli binární síť je ohraničená pro k = 1.
Pseudo-živá Petriho síť Značená Petriho síť (R, M0) je pseudoživá, jestliže všechny její přechody jsou pseudoživé. Přechod Ti je pesudoživý jestliže existuje aktivační sekvence S; M0 S > Mq , přičemž Mq uvolňuje přechod Ti. Neboli síť je pseudoživá, jestliže každý její přechod může být alespoň jednou přeskočen.
Živá Petriho síť Značená Petriho síť (R, M0) je živá, jestliže všechny její přechody jsou živé. Přechod Ti je živý jestliže pro libovolné dosažitelné značení M existuje aktivační sekvence S; M S > Mq , přičemž Mq uvolňuje přechod Ti. Neboli síť je živá, jestliže každý její přechod může být „kdykoli“ přeskočen.
Reverzibilní Petriho sítě Značená Petriho síť (R, M0) je reverzibilní, jestliže pro libovolné dosažitelné značení M existuje aktivační sekvence S, která uvede síť do původního značení M0. Neboli síť je reverzibilní jestliže pro libo-volné značení M dosažitelné z M0 existuje aktivační sekvence S; M S > M0.
Tato síť je pseudoživá, jelikož každý přechod může být alespoň jednou přeskočen. Aktivační sekvence T1T5T7T2T3T4 přivede síť z M0 do stavu, kdy se část
sítě nachází v deadlocku ( přechody T5 T6 a T7), takže síť není živá.
Aktivační sekvence T1T5T6T3 přivede síť z M0 do stavu, kdy žádný přechod není uvol-něn. Živá síť modeluje systém ve kterém se nevyskytuje deadlock.
T6
T5
P7
T7
P6
P1
T1
P4
T3
P5
T4
P2
T2
P3
P1
T1
P2
T2
P3
T3
P4
T4
P5
P1
T1
P2
T2
P3
T3
Přechody T1, T2, T3, T4 jsou živé � síť je živá.Místo P5 není ohraničené � síť není ohraničená.Po n opakováních sekvence T1 T2 lze pomocí nopakování sekvence T3 T4 uvést síť do původníhostavu � síť je reverzibilní.
Síť je živá.Síť není ohraničená.Síť není reverzibilní.

9
Poznámka pro hloubavé: Analýza Petriho sítí na výše uvedených příkladech pouze ilustruje možný postup při prokazo-vání jednotlivých vlastností. Pro automatizaci tohoto postupu se často nevyhneme konstrukci stavového diagramu, avšak v některých případech můžeme použít elegantnějšího postupu (re-dukce sítě, konzervativní komponenty atd...).
1.1.6. Časované Petriho sítě
Časované Petriho sítě patří do skupiny neautonomních Petriho sítí. Jako takové mají vazbu na své okolí, v tomto případě na čas. Pro úplnost uveďme, že všechny sítě uvedené v této kapitole jsou časované Petriho sítě s maximální rychlostí aktivace. P - časované Petriho sítě Definice: P-časovaná Petriho síť je uspořádaná trojice (R, M0, D) kde:
R je neznačená Petriho síť M0 je počáteční značení D je zobrazení z P do množiny nezáporných přirozených čísel, neboli D(Pi)=di
je čas přiřazený místu Pi . Princip: jestliže je značka umístěna do místa Pi potom musí zůstat v tomto místě nejméně po dobu di. Říkáme, že značka po dobu di není k dispozici. Po uplynutí této doby je značka k dispozici a může uvolnit další přechod.
Příklad: Výrobní linka se skládá ze vstupního skladu, soustruhu, brusky a výstupního skladu. Doba soustružení je 5 minut, doba broušení je 3 minuty. V počátečním stavu jsou stroje volné, ve vstupním skladu jsou 3 obrobky a výstupní sklad je prázdný.
P1 vstupní sklad P2 soustruh volný P3 soustruh obsazený P4 bruska volná P5 bruska obsazená P6 výstupní sklad
T - časované Petriho sítě
T1/0 d1=2
d2=3 T2/3 T1/2
d1=2
d2=3
P1
T1
P2
T2
d1=2
d2=3
P1
T1
P2
T2
d1=2
d2=3
P1
T1
P2
T2
P1
T1
P2
T2
(1,0)
(0,1)
(1,0)
t = 0 0<t<3 t = 3 3<t<5 t = 5 5<t<8 t = 8 8<t<10 stavový diagram
značka není k dispozici
P2 P4
P1 T1 T2 T3 P6
P3 P5
d3 = 5 d4 = 3

10
U T-časované Petriho sítě je každému přechodu Tj přiřazena doba dj > 0, po kterou je značka rezervována přechodem Tj.
Jak ilustruje obrázek, tak T-časovaná Petriho sítě může být jednoduše transformo-vána na P-časovanou Petri-ho síť. Obdobně lze transformovat P-časovanou Petriho síť na T-časovanou Petriho síť.
1.1.7. Interpretované Petriho sítě
Definice: interpretovaná Petriho síť má tři následující charakteristiky: - je synchronizovaná (aktivace přechodu je vázána na výskyt události) - je P-časovaná - zahrnuje operační část, jejíž stav je dán množinou proměnných V={ V1,V2, ...}. Tento - - stav je modifikován množinou operací O={ O1,O2, ... }, jež jsou asociovány k místům. - - Stav určuje hodnotu podmínek C={ C1,C2, ... }, které jsou asociovány k přechodům.
Z výše uvedené definice je zřejmé, že aktivace přechodu Tj je podmíněna třemi faktory: - zda je přechod Tj uvolněn (včetně toho, zda jsou uvolňující značky k dispozici vzhledem
k časům di vstupních míst přechodu Tj) - zda je podmínka Cj pravdivá - zda v tomto okamžiku nastala událost Ej
V případě, že přechod není vázán na žádnou vnější událost, potom místo Ej píšeme e. V případě, že přechod není vázán na žádnou podmínku potom píšeme (TRUE). Jestliže je značka vložena do místa Pi , potom provedeme operaci Oi a značka není k dispozici po dobu di.
P1 P2 P1 d1=0 P2 d2=0
T1’
T1 d1=x P1’ d1’=x
T1’’
P3 P4 P3 d3=0 P4 d4=0
V E
Interpretovaná Petriho síť
O C
Okolní prostředí
Operační částVýpočet proměnných
a podmínek
Řídicí částP-časovaná a
synchronizovanáPetriho síť
d1=0, V3←V3 + 1
E1.(V3 > 3)
d2=0, V3←V3 + 2
E2.(TRUE)
d3=2, identita
e.(V3=5)
d4=0, identita
P1
T1
P2
T2
P3
T3
P4

11
Specifikace a příklad interpretované Petriho sítě
Ve výše uvedené specifikaci i příkladu jsme používali nezjednodušenou notaci. V literatuře a aplikacích se samozřejmě můžeme setkat i se zjednodušenou notací, kde: - doba di.není uvedena v případě, že di=0
- operace Oi není uvedena, jestliže se nemění žádná proměnná (identita)
- událost Ei není uvedena, když přechod není vázán na žádnou vnější událost
- podmínka Ci není uvedena, jestliže je vždy splněna (TRUE).
Poznámka pro hloubavé: Díky zapojení Operační části do interpretované Petriho sítě, jsme omezili možnosti analýzy opírající se o autonomní Petriho síť, kde přeskok přechodu není vázán podmínkami Ci jejichž hodnota se může měnit v jiné části sítě.

12
1.2. Grafcet Grafcet, ve francouzštině "Graphe Fonctionnel de Connexion Etapes Transitions", je grafický návrhový nástroj pro řídicí systémy. Popisuje pouze realizovanou funkci, neboli automat v matematickém smyslu, nezávisle na technologii a konečné realizaci. Grafcet vychází z Petriho sítí, které jsou více matematickým nástrojem pro modelování systé-mů diskrétních událostí. Grafcet a je vhodný pro návrh algoritmů řízení PLC (programovatel-ných logických automatů). S trochou nadsázky lze říci, že Grafcet je zjednodušením Petriho sítí se zaměřením na řídicí systémy, ale především s jednoznačnou interpretací vstupů a výstu-pů. Srovnání Grafcetu s ostatními nástroji pro modelování systémů diskrétních událostí včetně Petriho sítí je podáno v [1]. Grafcet byl navržen v letech 1975-1977 francouzskou organizací AFCET "Association Fran-caise pour la Cybérnetique Economique et Technique" a v roce 1987 se stal mezinárodním standardem ( International Electrotechnical Commission 848 - Preparation of function charts for control systems).
1.2.1. Základní koncepce Grafcet obsahuje dva základní prvky : krok a přechod. Aktuální stav systému je v Grafcetu reprezentován aktivitou/neaktivitou všech kroků (neboli dosaženým značením). Každý krok (znázorněn čtverečkem s pořadovým číslem) se může vyskytovat pouze ve dvou základních stavech – buď může být aktivní anebo neaktivní . Aktivita kroku je v Grafcetu znázorněna značkou (tečka). Ke kroku lze vázat akci, jež je výstupem Grafcetu.
│ Kroky, které jsou aktivní na╔═╧═╗ začátku řídicího procesu (popisují║ 3 ║ počáteční stav systému) jsou╚═╤═╝ vyjádřeny symbolem počáteční krok
│ (značen dvojitým čtverečkem).Přechod je značen krátkou vodorovnou úsečkou. Přechod spolu s krokem tvoří dvojici vrcholů bipartitního orientovaného grafu ( hrana jde vždy z kroku do přechodu nebo z přechodu do kroku). Svislé hrany bez vyznačené orientace jsou hrany jdoucí shora dolů, hrany jdoucí zdola nahoru by měly být označeny šipkou. K přechodu je vázána podmínka, jež je vstupem Grafcetu.
┌─┴─┐ Přeskok přechodu reprezentuje změnu│ 1•│ AKTIVNÍ KROK stavu systému v závislosti na└─┬─┘ podmínkách (vstupech Grafcetu).─┼─ PŘECHOD
┌─┴─┐│ 2 │ NEAKTIVNÍ KROK└─┬─┘
Příklad: V počátečním stavu systému se vozík T nachází na kontaktu a. Po stlačení tlačítka s se pohy-buje doprava R. Po dosažení kontaktu b se vozík vrací ke kontaktu a pohybem vlevo L.
L R◄──┴──►
┌───────┐ ┌─┐│ T │ ─┴─┴─
│└o─────o┘ │ ──o o──a └──────────────────────────────┘b s

13
Řešení: ┌────┐│ ││ ╔═╧═╗ krok 1 - počáteční krok│ ║ 1 ║ kroky 2, 3 - provádí akce pro pohyb│ ╚═╤═╝ doprava respektive doleva│(1)─┼─ s.a přechod(1)- je přeskočen, když je krok 1│ ┌─┴─┐┌───────┐ a obě podmínky (s,a)jsou▲ │ 2 ├┤ R │ splněny│ └─┬─┘└───────┘ přechody(2)a(3)-jsou vázány na podmínky│(2)─┼─ b (b,a)│ ┌─┴─┐┌───────┐│ │ 3 ├┤ L ││ └─┬─┘└───────┘│(3)─┼─ a└────┘
1.2.2. Paralelismus a synchronizace
Každý přechod může mít několik kroků vstupních a několik kroků výstupních. Takové přecho-dy nazýváme konvergentní a divergentní AND přechody. Umožňují znázornit počátek (para-lelismus) a konec (synchronizaci) dvou a více paralelních sekvencí. Graficky paralelismus značíme dvojitou čarou za přechodem, synchronizaci pak dvojitou čarou před přechodem. Ná-sledující obrázek představuje divergentní AND před a po přeskoku přechodu (1) a konvergent-ní AND před a po přeskoku přechodu (2).
Paralelismus - Divergent AND Synchronizace - Convergent AND┌───┐ ┌───┐ ┌───┐│ 1•│ │ 4•│ │ 5•│└─┬─┘ └─┬─┘ └─┬─┘
(1)─┼─ a │ │╤══════╧══════╤ ╧═════╤═════╧│ │ (2)─┼─ b
┌─┴─┐ ┌─┴─┐ ┌─┴─┐│ 2 │ │ 3 │ │ 6 │└───┘ └───┘ └───┘
Přeskok při a=1 Přeskok při b=1
┌───┐ ┌───┐ ┌───┐│ 1 │ │ 4 │ │ 5 │└─┬─┘ └─┬─┘ └─┬─┘
(1)─┼─ a │ │╤══════╧══════╤ ╧═════╤═════╧│ │ (2)─┼─ b
┌─┴─┐ ┌─┴─┐ ┌─┴─┐│ 2•│ │ 3•│ │ 6•│└───┘ └───┘ └───┘
1.2.3. Výběr a spojení
Každý krok může mít několik vstupních a několik výstupních přechodů. V těchto případech jsou přechody nazývány konvergentní a divergentní OR přechody. Divergentní OR přechod znázorňuje výběr mezi dvěma popřípadě více následujícími větvemi. Konvergentní OR pře-chod znázorňuje spojení dvou popřípadě více větví do jedné.

14
Výběr - Divergentní OR Spojení - Konvergentní OR┌───┐ ┌───┐ ┌───┐│ 1•│ │ 4•│ │ 5 │└─┬─┘ └─┬─┘ └─┬─┘
│ (3)─┼─ c (4)─┼─ d┌──────┴──────┐ └─────┬─────┘
(1)─┼─ a (2)─┼─ b │┌─┴─┐ ┌─┴─┐ ┌─┴─┐│ 2 │ │ 3 │ │ 6 │└───┘ └───┘ └───┘
Přeskok Přeskoka=1, b=0 c=1
┌───┐ ┌───┐ ┌───┐│ 1 │ │ 4 │ │ 5 │└─┬─┘ └─┬─┘ └─┬─┘
│ (3)─┼─ c (4)─┼─ d┌──────┴──────┐ └─────┬─────┘
(1)─┼─ a (2)─┼─ b │┌─┴─┐ ┌─┴─┐ ┌─┴─┐│ 2•│ │ 3 │ │ 6•│└───┘ └───┘ └───┘
Při použití Grafcetu můžeme systém diskrétních událostí skládat z jednotlivých paralelních synchronizovaných sekvencí. Takovýto popis systému je díky své modularitě velmi přehledný a snadno rozšiřitelný. Příklad: Po sepnutí tlačítka s se začnou vozíky T1 a T2 pohybovat z kontaktů a1, a2 doprava. Dosáhne-li některý z vozíků kontaktu b, zastaví se a čeká na druhý vozík. Po setkání v bodech b, se oba vozíky vrací do bodů a1, a2.
L1 R1 L2 R2 ┌─┐◄──┴──► ◄──┴──► ─┴─┴─
┌───────┐ ┌───────┐ ──o o──│ T1 │ │ T2 │ s└o─────o┘ └o─────o┘
a1└────────────────────────┘b1 a2└─────────────────────────┘b2┌──────┐ ┌─────────────┐│ ╔═╧═╗ ╔═╧═╗ ││ ║ 1 ║ ║ 2 ║ ││ ╚═╤═╝ ╚═╤═╝ ││ │ (synchronizace) │ ││ ╧════════════╤════════════╧ ││ ─┼─ s.a1.a2 ││ ╤════════════╧════════════╤ ││ │ (paralelismus) │ ││ ┌─┴─┐┌─────┐ ┌─┴─┐┌─────┐ ││ │ 3 ├┤ R1 │ │ 4 ├┤ R2 │ ││ └─┬─┘└─────┘ └─┬─┘└─────┘ │▲ ─┼─ b1 ─┼─ b2 ▲│ ┌─┴─┐ ┌─┴─┐ ││ │ 5 │ │ 6 │ ││ └─┬─┘ └─┬─┘ ││ │ (synchronizace) │ ││ ╧════════════╤════════════╧ ││ ─┼─ 1 ││ ╤════════════╧════════════╤ ││ │ (paralelismus) │ ││ ┌─┴─┐┌─────┐ ┌─┴─┐┌─────┐ ││ │ 7 ├┤ L1 │ │ 8 ├┤ L2 │ ││ └─┬─┘└─────┘ └─┬─┘└─────┘ ││ ─┼─ a1 ─┼─ a2 │└──────┘ └─────────────┘

15
Model jasně ukazuje dvě paralelní sekvence zahájené divergetními AND přechody (odpovídají rozjezdům vozíků) a ukončené konvergentními AND přechody (odpovídají vzájemnému čekání vozíků na startu a čekání vozíků na zpáteční cestu).
1.2.4. Pravidla pro tvorbu Grafcetu
Konstrukce modelu pomocí Grafcetu předpokládá pochopení a přesné dodržování následují-cích pravidel, která jsou obsažena v mezinárodním standardu. Pravidlo 1: Počáteční stav
Počáteční stav je dán počátečními kroky (krokem), které jsou definovány jako ak-tivní na počátku vývoje systému.
Pravidlo 2: Uvolnění a přeskok přechodu
Každý přechod se může vyskytovat pouze v jednom ze dvou stavů: buď je uvolněn nebo neuvolněn. Přechod je uvolněn právě tehdy, když všechny předcházející kro-ky sbíhající se v tomto přechodu jsou aktivní. Přechod je přeskočen, jestliže je uvolněn a podmínka jeho přechodu je splněna ("TRUE").
Pravidlo 3: Vývoj aktivních kroků
Přeskočení přechodu zároveň uvede do aktivního stavu bezprostředně následující krok (kroky) a deaktivuje krok (kroky) bezprostředně předcházející.
Přechod (1) není uvolněn Přechod (2) je uvolněn
┌───┐ ┌───┐ ┌───┐ ┌───┐│ 1•│ │ 2 │ │ 4•│ │ 5•│└─┬─┘ └─┬─┘ └─┬─┘ └─┬─┘
│ │ │ │╧═════╤═════╧ ╧═════╤═════╧
(1)─┼─ a (2)─┼─ b┌─┴─┐ ┌─┴─┐│ 3 │ │ 6 │└───┘ └───┘
Pro b=1 je přechod (2) přeskočen┌───┐ ┌───┐│ 4 │ │ 5 │└─┬─┘ └─┬─┘
│ │╧═════╤═════╧
(2)─┼─ b┌─┴─┐│ 6•│└───┘
Pravidlo 4: Současné přeskočení více přechodů Dvojitou čárou před přechodem (synchronizace) a za přechodem (paralelismus) znázorňujeme přechody, které mají být přeskočeny současně (viz. příklad se syn-chronizací vozíků). Jestliže jsou tyto přechody kresleny z estetických důvodů od-děleně (viz. následující obrázek), označíme je hvězdičkou a rozšíříme podmínku přechodu o odpovídající proměnnou (boolovská proměnná X11 má hodnotu TRUE, když je krok 11 aktivní).

16
Současná aktivace přechodů: ┌───┐ ┌───┐ ┌───┐ ┌───┐│10 │ │11 │ │10 │ │11 │└─┬─┘ └─┬─┘ └─┬─┘ └─┬─┘
│ │ │ │╧═════╤═════╧ │ │
─┼─ a odpovídá * ─┼─ a.X11 * ─┼─ a.X10╤═════╧═════╤ │ ││ │ │ │
┌─┴─┐ ┌─┴─┐ ┌─┴─┐ ┌─┴─┐│12 │ │13 │ │12 │ │13 │└───┘ └───┘ └───┘ └───┘
Pravidlo 5: Současná aktivace a deaktivace kroku Jestliže má být krok současně aktivován i deaktivován, je priorita dána aktivaci kroku. Krok tedy zůstane aktivní.
Pravidlo 6: Odstranění nekoncepčnosti
┌───┐ V případě, kdy a=b=1, se v Grafcetu│ 1•│ aktivují kroky 2 a 3. Tato situace└─┬─┘ je nežádoucí, jelikož došlo k
│ paralelizaci, jež by měla být┌──────┴──────┐ popsána divergentním AND (tedy nikoli
(1) ─┼─ a (2) ─┼─ b dvěma přechody pod jednoduchou┌─┴─┐ ┌─┴─┐ vodorovnou čarou, ale jen jedním│ 2 │ │ 3 │ přechodem a to nad dvojitou└───┘ └───┘ vodorovnou čarou).
Takovýto způsob popisu vede na koncepční (interpretační) chyby a tato část grafcetového mo-delu se musí transformovat do jednoznačné formy. Při odstranění této nekoncepčnosti je po-třeba vědět, jaký systém vlastně chceme modelovat. V úvahu přicházejí dvě možnosti:
A) chceme modelovat rozvětvení (divergentní exclusive OR), tudíž pouze jeden z kroků 2 a 3 bude aktivní. V tomto případě doplníme podmínku přechodu (2) o negaci podmínky přechodu (1) - viz model -A- na obrázku níže). Tím jsme znemožnili současný přeskok přechodu (1) a (2). Zároveň jsme rozhodli, že prioritu má krok 2 před krokem 3, jeli-kož v případě, kdy a=b=1 je aktivován krok 2. Tento systém se tedy mohl vyvíjet dvě-ma možnými způsoby:
- je aktivován pouze krok 2 - je aktivován pouze krok 3
┌───┐┌───┐ │ 1•││ 1•│ └─┬─┘└─┬─┘ │
│ ┌────────────┼────────────┐┌──────┴──────┐ (1)─┼─ a.b' (3)─┼─ a.b (2)─┼─ a'.b
(1)─┼─ a (2)─┼─ b.a' │ ╤══╧══╤ │┌─┴─┐ ┌─┴─┐ │ │ │ ││ 2 │ │ 3 │ ├─────────┘ └─────────┤└───┘ └───┘ ┌─┴─┐ ┌─┴─┐
│ 2 │ │ 3 │└───┘ └───┘
-A- -B-
B) chceme modelovat systém, v němž se situace může vyvíjet třemi možnými způsoby: - je aktivován pouze krok 2 - je aktivován pouze krok 3 - jsou současně aktivovány kroky 2 a 3

17
Model takového systému upravíme následujícím způsobem ( viz model -B-): - doplníme podmínku přechodu (1) o negaci podmínky (2) - doplníme podmínku přechodu (2) o negaci podmínky (1) - přidáme přechod (3) vázaný na obě podmínky
Takto popsané systémy jsou již bez koncepčních chyb a jednoznačně graficky znázorňují jeho vlastnosti.
1.2.5. Akce spojené s kroky
Akce bez paměti (probíhající akce) - vykonává se do té doby, pokud krok N s ním spojený je aktivní (proměnná XN reprezentu-
je aktivitu kroku N)
│┌─┴─┐ ┌───────────┐ XN ┌───────────┐│ N ├─┤ AKCE A │ ───┘─ ─ ─ ─ ─ -└────└─┬─┘ └───────────┘─┼─ c A ┌───────────┐│ ───┘─ ─ ─ ─ ─ -└────
Akce bez paměti se zpožděním - je vykonávána od okamžiku, kdy uplynulo zpoždění od aktivace s ním spojeného kroku.
Akce je ukončena ve chvíli, kdy krok přestává být aktivní.
XN ┌──────────┐┌─┴─┐ ┌───┬────────────┐ ───┘─ ─ ─ ─ ─ └────│ N ├─┤ D │AKCE A D=5s │└─┬─┘ └───┴────────────┘ A ┌─────┐─┼─ c ────────┘- - -└────│ ├────┤
5s
Akce bez paměti s časovým limitem - je vykonávána, je-li krok aktivní a nebyl-li překročen časový limit od počátku aktivace
kroku
│ XN ┌──────────┐┌─┴─┐ ┌───┬────────────┐ ───┘- - - - - └────│ N ├─┤ L │AKCE A L=10s│└─┬─┘ └───┴────────────┘ A ┌───────┐─┼─ c ───┘- - - -└───────│ ├───────┤
10s
Akce bez paměti s podmínkou - je vykonávána, je-li krok aktivní a s ním spojená podmínka “b“je splněna ("TRUE")
│ XN ┌────────────┐┌─┴─┐ ┌───┬─────────────┐ ───┘─ ─ ─ ─ ─ ─ └───│ N ├─┤ C │AKCE A if "b"│ b ┌─┐ ┌───────└─┬─┘ └───┴─────────────┘ ───────┘─└──┘─ ─ ─ ──┼─ e A ┌─┐ ┌───┐│ ───────┘─└──┘─ ─└───

18
Akce s pamětí - je spojena se dvěma kroky, jedním krokem startovacím (start, set) a druhým krokem ukončo-
vacím (stop, reset). Akce začíná s náběžnou hranou startovacího kroku a končí s náběžnou hranou ukončovacího kroku
┌─┴─┐ ┌───┬────────────┐│ N ├─┤ S │START AKCE A│ XN ┌───┐└─┬─┘ └───┴────────────┘ ───┘- -└─────────────┼─ c│ XM ┌─┐
───────────────┘-└──│
┌─┴─┐ ┌───┬───────────┐ A ┌───────────┐│ M ├─┤ S │STOP AKCE A│ ───┘- - - - - -└────└─┬─┘ └───┴───────────┘─┼─ d│
Akce s pamětí s časovým limitem - vykonává se po náběžné hraně startovacího kroku. Končí buď po uplynutí daného časové-
ho limitu nebo s náběžnou hranou ukončovacího kroku. Akci pro tři různé časové limity znázorňuje následující obrázek.
│ XN ┌───┐┌─┴─┐ ┌───┬────────────┐ ───┘- -└───────────────│ N ├─┤SL │START A L=5s│└─┬─┘ └───┴────────────┘ XM ┌─┐─┼─ c ───────────────┘-└─────│
A ┌──┐│ ───┘- └────────────────
┌─┴─┐ ┌───┬───────────┐ ├──┤│ M ├─┤ S │ STOP A │ L1└─┬─┘ └───┴───────────┘ A ┌─────┐─┼─ d ───┘- - -└─────────────│ ├─────┤
L2A ┌───────────┐
───┘- - - - - -└───────├─────────────────┤
L3
Některé další varianty komplexních akcí může zvídavý čtenář nalézt přímo v normě IEC 848.
1.2.6. Podmínky přechodu a jejich vyjádření
Podmínka přechodu může být vyjádřena ve čtyřech rozdílných formách: - slovní vyjádření - logický výraz - grafické vyjádření - časově závislé vyjádření Ve všech případech je vždy výsledek podmínky boolská proměnná, která nabývá hodnot "1" TRUE nebo "0" FALSE.

19
Všechna tři následující vyjádření podmínky přechodu ( slovní vyjádření, logický výraz, gra-fické vyjádření) jsou si rovnocenná.
┌───┐│ 1 │└─┬─┘─┼─ Pumpa P běží a (ventil Va nebo ventil Vb je otevřen)
┌─┴─┐│ 2 │└───┘┌───┐ ┌───┐ ┌───┐│ 1 │ │ 1 │ P ────────────┤ &│└─┬─┘ └─┬─┘ │ │─┼─ P.(Va + Vb) ─┼─ d ┌───┐ │ ├──── d
┌─┴─┐ ┌─┴─┐ Va──────┤ 1│ │ ││ 2 │ │ 2 │ │ ├─┤ │└───┘ └───┘ Vb──────┤ │ └───┘
└───┘
Přeskok přechodu nemusí záviset pouze na logické hodnotě podmínky, ale může být závislý na její změně (0→1 nebo 1→0). Pak výskyt událostí tvoří spádové respektive náběžné hrany podmínek.
┌───┐ ┌───┐ ┌───┐│ 1 │ │ 1 │ │ 1 │└─┬─┘ └─┬─┘ └─┬─┘─┼─ c ─┼─ ↑c ─┼─ ↓c
┌─┴─┐ ┌─┴─┐ ┌─┴─┐│ 2 │ │ 2 │ │ 2 │└───┘ └───┘ └───┘
pozitivní logická náběžná hrana sestupná hranaúroveň signálu c signálu c signálu c
Rozdíl chování dvou systémů, kde jeden je podmíněn logickou úrovní a druhý náběžnou hra-nou je znázorněn níže.
┌───┐ ┌───┐│ 1•│ │ 4•│└─┬─┘ └─┬─┘
(1)─┼─ a (3)─┼─ ↑a┌─┴─┐ ┌─┴─┐│ 2 │ │ 5 │└─┬─┘ └─┬─┘
(2)─┼─ a (4)─┼─ ↑a┌─┴─┐ ┌─┴─┐│ 3 │ │ 6 │└───┘ └───┘
pro a=1 jsou přechody při náběžné hraně signálu a(1) a (2) přeskočeny je přeskočen pouze přechod (3)
┌───┐ ┌───┐│ 1 │ │ 4 │└─┬─┘ └─┬─┘
(1)─┼─ a (3)─┼─ ↑a┌─┴─┐ ┌─┴─┐│ 2 │ │ 5•│└─┬─┘ └─┬─┘
(2)─┼─ a (4)─┼─ ↑a┌─┴─┐ ┌─┴─┐│ 3•│ │ 6 │└───┘ └───┘

20
U podmínek závislých na logické úrovni vede přeskok přechodu (1) na nestabilní stav (značka v kroku 2), který končí ve stabilním stavu (značka v kroku 3). U podmínek závislých na náběžné hraně signálu vede přeskok přechodu (3) do stabilního stavu reprezentovaného přítomností značky v kroku 5. Další přeskok do kroku 6 může nastat až při další náběžné hraně signálu a. Podmínky přechodu mohou být dány také kombinací logické úrovně a náběžné/sestupné hrany:
┌───┐│ 1•│ c ┌───────────────└─┬─┘ ─────────┘- - - - - - - -─┼─ c.↑e e ┌─┐ ┌─────────
┌─┴─┐ ──┘-└──────────┘- - - - -│ 2 │ X2 ┌─────────└───┘ ───────────────┘- - - - -
Časově závislé vyjádření Časově závislou podmínku přechodu lze zapsat takto:
┌───┐ X1───────────────┐│ 1•│ - - - - - - - -└─────────└─┬─┘ a ┌────────┐─┼─ T1/a/T2 ────────┘- - - - └───────
┌─┴─┐ T1/a/T2 ┌────┐│ 2 │ ───────────────┘- - └────└───┘ X2 ┌─────────
───────────────┘- - - - -├──────┤ ├──┤
T1 T2
Podmínka přechodu T1/a/T2 nabude hodnoty TRUE po době T1 od změny podmínky a z 0 na 1, podmínka se vrátí na FALSE po době T2 od změny proměnné a z 1 na 0. Když časově závis-lé vyjádření neobsahuje zpoždění T2, potom píšeme pouze T1/a. Pokud podmínka a vyjadřuje stav vstupního kroku, pak se jedná pouze o čisté zpoždění při změně aktivity kroků:
┌─┴─┐│ 1•│ X1 ┌──────────┐└─┬─┘ ────┘ - - - - -└──────────┼─ 10s/X1 10s
┌─┴─┐ ├──────────┤│ 2 │ X2 ┌─────────└───┘ ───────────────┘- - - - -
1.2.7. Strukturovací prostředky Grafcetu
Při návrhu grafcetového modelu složitého systému je nezbytné použít strukturovaný přístup, který umožní dekomponovat systém na několik vzájemně propojených modelů. Nástroje umožňující jistý stupeň strukturování, jsou definovány ve standartu Grafcetu. Jsou jimi opa-kování shodné sekvence a makro (detailní zobrazení kroku). Jelikož interpretace opakování shodné sekvence je díky použití operátoru * zavádějící, uvádíme pouze makro, jež má dosta-tečné vyjadřovací schopnosti pro opakování reentrantních sekvencí.

21
Makro ( detailní zobrazení kroku ) Krok definovaný na určité úrovni může být detailně zobrazen na nižší úrovni hierarchie. Tak jsou globálně definované akce vyšší úrovně dekomponovány do sekvencí elementárních akcí nižší úrovně, které začínají jedním a končí jiným krokem.
┌───┐. │31 │
. └─┬─┘│ . ├─────────┐
─┼─ a . ─┼─ b ─┼─ c│ . ┌─┴─┐ ┌─┴─┐
┌─┴─┐ . │32 │ │34 ││ 3 │ └─┬─┘ └─┬─┘└─┬─┘ . ─┼─ d ─┼─ e
│ . ┌─┴─┐ │─┼─ g . │33 │ ││ . └─┬─┘ │
. ─┼─ f │. ├─────────┘
┌─┴─┐│35 │└───┘
1.3. Srovnání Grafcetu a Petriho sítí Z výše uvedených modelů je zřejmé, že pro srovnání s Grafcetem je vhodná interpretovaná Petriho síť (IPS). Podívejme se nejdříve na společné rysy obou modelů. Oba modely lze reprezentovat bipartitním grafem. Petriho sítě mají dva typy uzlů – místa a přechody. Grafcet má též dva typy uzlů – kroky a přechody. Grafická reprezentace obou mode-lů je podobná, v obou případech je vývoj systému (změna značení) vázán na vnější události. Podívejme se nyní na odlišnosti Grafcetu a Petriho sítí. - Rozdíl 1: Všechny přechody souběžně aktivovatelné v Grafcetu jsou také souběžně aktivová-
ny (viz pravidlo 6 ). Na druhou stranu Petriho síť umožňuje aktivovat pouze jeden ze dvou přechodů uvolněných stejnou značkou (viz efektivní konflikt).
- Rozdíl 2: Značení kroku v Grafcetu lze reprezentovat jedním bitem, zatímco značení Petriho sítě je potřeba reprezentovat celým nezáporným číslem.
- Rozdíl 3: Podmínka vázaná k přechodu u Grafcetu může záviset na značení, což není pravda u IPS.
- Rozdíl 4: Obecná Petriho síť umožňuje přiřadit hranám váhy, což není pravda u Grafcetu. Rozdíly 1 a 2 mají zásadní význam a jejich důsledky lze vidět v následujících obrázcích.
Souběžná aktivace dvou přechodů v Grafcetu versus efektivní konflikt v IPS
Přeskok v Grafcetu při události E1 Dvě možné aktivace v IPS při události E1 E1 E1 nebo
E1 E1 E1 E1 E1 E1

22
Reaktivace kroku a současná aktivace kroku v Grafcetu versus aktivace v IPS
Rozdíl 3 nemá zásadní význam, jelikož pomocí přiřazení operací místům můžeme v IPS do-sáhnout obdobného efektu, jaký má podmínka závislá na značení u Grafcetu. Rozdíl 4 také nemá zásadní význam, jelikož obecnou Petriho síť lze transformovat na Petriho síť u které je váha hrany vždy rovna 1 (i když je to obecně značně komplikované).
1.4. Závěr V této kapitole byly prezentovány různé modely systémů diskrétních událostí. Pokusme se shrnout základní rysy těchto modelů. Základním modelem je autonomní Petriho síť. Umožňuje specifikovat „jak to funguje“, neboli vnitřní logiku modelovaného systému. Na základě modelu autonomní Petriho sítí lze hodnotit fungování systému, neboli analyzovat vlastnosti autonomní Petriho sítě. Neautonomní Petriho sítě (jsou vázané na vnější prostředí) mají dvě základní oblasti použití: - synchronizované Petriho sítě (umožňují modelovat vývoj systému podmíněného vnějšími
událostmi) vhodné pro popis řídicího systému - časované Petriho sítě (umožňují vzít v úvahu čas) vhodné pro hodnocení výkonnosti sytému
(doba výpočtu programu, výkon výrobní linky, propustnost komunikačního kanálu). Grafcet je zaměřen na specifikaci programu pro PLC. Jasně definuje vstupy, výstupy a jejich vztah. Použití Gracetu v průmyslových aplikacích se opírá o fakt, že je mezinárodní normou. Grafcet vychází z Petriho sítí, ale jejich znalost není nezbytná pro pochopení Grafcetu (napří-klad kapitola 1.2. je nezávislá na kapitole 1.1.). Autoři skript děkují panu Janu Kadlecovi za průkopnickou činnost v oblasti Grafcetu a panu René Davidovi za četné rady, náměty a připomínky obsažené v této kapitole.
Reaktivace v Grafcetu Aktivace v IPSpři události E1 při události E1
E1
E2 E1
E2
E1
E2
Současný přeskok v Grafcetu při E1 Aktivace v IPS při E1 E1 E1
E1 E1 E1 E1