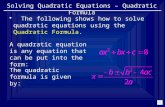
MAT121: SECTION 3.1 QUADRATIC FUNCTIONS OF A QUADRATIC FUNCTION: GRAPH • Shape: Parabola – it...
Transcript of MAT121: SECTION 3.1 QUADRATIC FUNCTIONS OF A QUADRATIC FUNCTION: GRAPH • Shape: Parabola – it...
Section 3.1: Quadratic Functions 1
MAT121: SECTION 3.1
QUADRATIC FUNCTIONS
ANATOMY OF A QUADRATIC FUNCTION: GRAPH
• Shape: Parabola – it may open upwards or down.
• Vertex: Represented as (ℎ, 𝑘). It can be the maximum or minimum point depending on how the
parabola opens.
• Axis of Symmetry: Pass through the vertex. Always represented as the equation, 𝑥 = ℎ.
Quadratic functions can be expressed in two ways:
• Polynomial Form: 𝑓 𝑥 = 𝑎𝑥! + 𝑏𝑥 + 𝑐
• Vertex Form: 𝑓 𝑥 = 𝑎 𝑥 − ℎ ! + 𝑘
VERTEX FORM
𝑓 𝑥 = 𝑎 𝑥 − ℎ ! + 𝑘 Note its similarity to the transformations from Section 2.6
• The sign of a determines the direction in which the parabola opens and whether the vertex is a
maximum or minimum point.
o a > 0 (positive) then the parabola opens upward and the vertex is a minimum.
o a < 0 (negative) then the parabola opens downward and the vertex is a maximum.
• In this form, the vertex is easily determined. (ℎ, 𝑘) are the coordinates of the vertex.
Section 3.1: Quadratic Functions 2
Consider 𝑓 𝑥 = 𝑥 − 1 ! + 2
• Does the parabola open up or down? Why? Up, because a is positive.
• State the vertex. (1, 2)
• Is this a max or min? Minimum
• State the Axis of Symmetry. 𝑥 = 1
• State the Domain and Range. 𝐷𝑜𝑚𝑎𝑖𝑛: −∞,∞ 𝑅𝑎𝑛𝑔𝑒: [2,∞)
Consider 𝑓 𝑥 = 𝑥 + 4 ! + 1.
The function can be rewritten to fit the model. 𝑓 𝑥 = 𝑥 − −4 ! + 1
• State the vertex. (−4, 1)
• Is this a max or min? Minimum
• State the Axis of Symmetry. 𝑥 = −4
• Graph the function. What are the x- and y-intercepts?
x-intercepts: Consider the vertex. It’s above the x-axis and is the minimum, so no x-intercepts.
y-intercept: 𝑓 0 = 0+ 4 ! + 1 = 17 so the y-intercept is (0, 17)
ON YOUR OWN
Consider 𝑓 𝑥 = −2 𝑥 + 6 ! − 5.
• Does the parabola open up or down? Down
• State the vertex. Is it a max or min? Max
• State the y-intercept. (0,−77)
• State the Domain and Range. 𝐷: −∞,∞ 𝑅: (−∞,−5]
• Graph it.
Section 3.1: Quadratic Functions 3
POLYNOMIAL FORM
𝑓 𝑥 = 𝑎𝑥! + 𝑏𝑥 + 𝑐
• The sign of a determines the direction in which the parabola opens and whether the vertex is a
maximum or minimum point.
Consider 𝑓 𝑥 = 3𝑥! − 6𝑥 + 1.
• Does the parabola open up or down? Up, because the coefficient on x2 is positive.
• State the y-intercept. 𝑓 0 = 1, so the y-intercept is (0,1).
• Convert the function to vertex form by completing the square.
3𝑥! − 6𝑥 + 1
3(𝑥! − 2𝑥 )+ 1
3 𝑥! − 2𝑥 + 1 + 1− (3 ∙ 1)
3 𝑥 − 1 ! − 2
• State the vertex. (1,−2) It’s a minimum.
• Find the x-intercepts. Recall (𝑥, 0) represents the x-intercept.
Using the vertex form.
3 𝑥 − 1 ! − 2 = 0
3 𝑥 − 1 ! = 2
𝑥 − 1 ! =23
𝑥 − 1 = ±23
𝑥 = 1±23
Using the polynomial form and DQUAD.
3𝑥! − 6𝑥 + 1
𝑎 = 3
𝑏 = −6
𝑐 = 1
𝑥 = − − 6 ± 24
6
𝑥 = 6 ± 2 6
6 = 3± 63
Section 3.1: Quadratic Functions 4
FINDING AN EXPRESSION FOR VERTEX
Converting the polynomial model to the vertex model yields (page 323)
𝑓 𝑥 = 𝑎 𝑥 +𝑏2𝑎
!
+ 𝑐 −𝑏!
4𝑎
where ℎ!!!""#$%&'() !" !"#$"% = − !!!
and 𝑘!!!""#$%&'() !" !"#$"% = 𝑐 − !!
!!
Make it easier!
Given 𝑓 𝑥 = 𝑎𝑥! + 𝑏𝑥 + 𝑐, the x-coordinate of the vertex is found from – !!!
.
The y-coordinate of the vertex is found from 𝑓 – !!!
.
Consider 𝑓 𝑥 = 2𝑥! + 8𝑥 + 3. Find the vertex.
ℎ = 𝑥 𝑐𝑜𝑜𝑟𝑑𝑖𝑎𝑛𝑡𝑒 𝑜𝑓 𝑉𝑒𝑟𝑡𝑒𝑥 = −8
2 2 = −2
𝑘 = 𝑦 𝑐𝑜𝑜𝑟𝑑𝑖𝑎𝑛𝑡𝑒 𝑜𝑓 𝑉𝑒𝑟𝑡𝑒𝑥 = 𝑓 −2 = 2 −2 ! + 8 −2 + 3 = −5
Thus the vertex is (−2,−5).
ON YOUR OWN
Find the vertex of 𝑓 𝑥 = −𝑥! − 6𝑥 + 2.
ℎ = 𝑥 𝑐𝑜𝑜𝑟𝑑𝑖𝑎𝑛𝑡𝑒 𝑜𝑓 𝑉𝑒𝑟𝑡𝑒𝑥 = 6
2 −1 = −3
𝑘 = 𝑦 𝑐𝑜𝑜𝑟𝑑𝑖𝑎𝑛𝑡𝑒 𝑜𝑓 𝑉𝑒𝑟𝑡𝑒𝑥 = 𝑓 −3 = − −3 ! − 6 −3 + 2 = 11
Thus the vertex is (−3, 11).
Section 3.1: Quadratic Functions 5
(−3, 11)
GRAPHING A QUADRATIC
1. Determine if parabola opens up or down.
2. Find the vertex.
3. Find all intercepts.
4. State the Domain and Range.
5. Sketch the graph.
Consider 𝑓 𝑥 = −𝑥! − 4𝑥 − 7.
1. Opens down.
2. Vertex: ℎ = − !!! !!
= −2
𝑘 = 𝑓 −2 = − −2 ! − 4 −2 − 7 = −3
(−2,−3) Maximum
3. x-intercept: Via DQUAD – none
y-intercept: (0,−7)
4. Domain: −∞,∞ Range: (−∞,−3]
5.
Section 3.1: Quadratic Functions 6
APPLICATIONS
Suppose that a family wants to fence in an area of their yard for a vegetable garden to keep out deer.
One side is already fenced from the neighbor’s property.
• If the family has enough money to buy 160 feet of fencing, what dimensions would produce the
maximum area for the garden?
• What is the maximum area?
1. Start with what you know. 𝑃𝑒𝑟𝑖𝑚𝑒𝑡𝑒𝑟 = 2𝑥 + 𝑦 = 160
2. What is being maximized? 𝐴𝑟𝑒𝑎 = 𝑥𝑦
3. Solve perimeter for y and substitute into area to create the quadratic expression.
2𝑥 + 𝑦 = 160
𝑦 = −2𝑥 + 160
𝐴𝑟𝑒𝑎 = 𝑥𝑦 = 𝑥 −2𝑥 + 160 = −2𝑥! + 160𝑥
4. Since the vertex is the maximum point of this area function, find the x-coordinate of the vertex.
𝑥 = −1602 −2 = 40 𝑓𝑒𝑒𝑡
NOTE: Substituting the x-value into the quadratic expression yields the maximum area not the y-dimension.
To find the y-dimension of the garden, substitute x into 𝑦 = −2𝑥 + 160
𝑦 = −2 40 + 160 = 80 𝑓𝑒𝑒𝑡
5. Find the maximum area.
𝐴𝑟𝑒𝑎 = 𝑥𝑦 = 40 80 = 3200 𝑠𝑞 𝑓𝑒𝑒𝑡
Section 3.1: Quadratic Functions 7
In the shot put, an athlete throws the shot at an angle of 65°. Its height, 𝑔(𝑥), in feet, can be modeled
𝑔 𝑥 = −0.04𝑥! + 2.1𝑥 + 6.1
where x is the shot’s horizontal distance, in feet, from its point of release.
• What is the horizontal distance of the shot at which the maximum height occurs?
• What is the maximum height?
• What is the shot’s maximum horizontal distance (distance of the throw)?
• At what distance does the shot reach 5 feet in height?
1. The horizontal distance of the maximum height is the x-coordinate of the vertex.
𝑥 = −2.1
2 −0.04 = 26.25 𝑓𝑒𝑒𝑡
2. The maximum height is found by
𝑔 26.25 = 33.66 𝑓𝑒𝑒𝑡
3. To find the distance of the throw, calculate the x-intercepts.
Via DQUAD, 𝑥 = −2.76 𝑎𝑛𝑑 55.26. Choose the one that makes
sense. 𝑥 = 55.26 𝑓𝑒𝑒𝑡
4. We’ve been given a y-value and asked to find the x-value.
5 = −0.04𝑥! + 2.1𝑥 + 6.1
0 = −0.04𝑥! + 2.1𝑥 + 1.1
Via DQUAD, 𝑥 = 53.02 𝑓𝑒𝑒𝑡