Holt Algebra 2 7-1 Exponential Functions, Growth, and Decay exponential function baseasymptote...

Holt Algebra 2

7-1 Exponential Functions, Growth, and Decay

exponential functionbase asymptoteexponential growth and decay

Vocabulary

Write and evaluate exponential expressions tomodel growth and decay situations.

Objective

Holt Algebra 2


NotesIn 2000, the world population was 6.08 billion and was increasing at a rate 1.21% each year.1. Write a function for world population. Does

the function represent growth or decay?

2. Predict the population in 2020.

The value of a $3000 computer decreases about 30% each year.3. Write a function for the computer’s value.

Does the function represent growth or decay?

4. Predict the value in 4 years.

Holt Algebra 2


Growth that doubles every year can be modeled by using a function with a variable as an exponent. This function is known as an exponential function. The parent exponential function is f(x) = bx, where the base b is a constant and the exponent x is the independent variable.

Holt Algebra 2


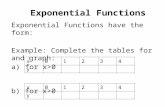
The graph of the parent function f(x) = 2x is shown. The domain is all real numbers and the range is {y|y > 0}.

Holt Algebra 2


Notice as the x-values decrease, the graph of the function gets closer and closer to the x-axis. The function never reaches the x-axis because the value of 2x cannot be zero. In this case, the x-axis is an asymptote. An asymptote is a line that a graphed function approaches as the value of x gets very large or very small.

Holt Algebra 2


A function of the form f(x) = abx, with a > 0 and b > 1, is an exponential growth function, which increases as x increases. When 0 < b < 1, the function is called an exponential decay function, which decreases as x increases.

Holt Algebra 2


Negative exponents indicate a reciprocal. For example:

Remember!

In the function y = bx, y is a function of x because the value of y depends on the value of x.

Remember!

Holt Algebra 2


Tell whether the function shows growth or decay. Then graph.

Example 1A: Graphing Exponential Functions

Step 1 Find the value of the base.

3104

x

f x

The base , ,is less than 1.

This is an exponential decay

function.

34 3

410

x

f x

Holt Algebra 2


Example 1A ContinuedStep 2 Graph the function by using a table of values.

x 0 2 4 6 8 10 12f(x) 10 5.6 3.2 1.8 1.0 0.6 0.3

Holt Algebra 2


Tell whether the function shows growth or decay. Then graph.

Example 1B: Graphing Exponential Functions


g(x) = 100(1.05)x

The base, 1.05, is greater than 1. This is an exponential growth function.

g(x) = 100(1.05)x

Holt Algebra 2


Tell whether the function p(x) = 5(1.2x) shows growth or decay. Then graph.


Example 1C

p(x) = 5(1.2 x) The base , 1.2, is greater than 1. This is an exponential growth function.

Holt Algebra 2


Step 2 Graph the function by using a table of values.

x –12 –8 –4 0 4 8 10f(x) 0.56 1.2 2.4 5 10.4 21.5 30.9

Example 1C Continued

Holt Algebra 2


You can model growth or decay by a constant percent increase or decrease with the following formula:

In the formula, the base of the exponential expression, 1 + r, is called the growth factor. Similarly, 1 – r is the decay factor.

Holt Algebra 2


Clara invests $5000 in an account that pays 6.25% interest per year. What will her investment be worth in seven years?

Example 2A: Economics Application

Step 1 Write a function to model the growth in value of her investment.

f(t) = a(1 + r)t Exponential growth function.

Substitute 5000 for a and 0.0625 for r.

f(t) = 5000(1 + 0.0625)t

f(t) = 5000(1.0625)t Simplify.

Holt Algebra 2


Clara invests $5000 in an account that pays 6.25% interest per year. What will her investment be worth in seven years?

Example 2A: Economics Application

Step 2 Use function to evaluate at t = 7.

f(t) = 5000(1.0625)t Substitute 7 for t.

Holt Algebra 2


In 1981, the Australian humpback whale population was 350 and increased at a rate of 14% each year since then. Write a function to model population growth.

P(t) = a(1 + r)t

Substitute 350 for a and 0.14 for r.

P(t) = 350(1 + 0.14)t

P(t) = 350(1.14)t Simplify.

Exponential growth function.

Example 2B

Holt Algebra 2


A city population, which was initially 15,500, has been dropping 3% a year. Write an exponential function. What will the population be after ten years?

Example 3: Depreciation Application

f(t) = a(1 – r)t Substitute 15,500 for a and 0.03 for r.

f(t) = 15,500(1 – 0.03)t

f(t) = 15,500(0.97)t Simplify.

Exponential decay function.

f(t) = 15,500(0.97)10 =11,430 t=10 for ten years.

Holt Algebra 2


NotesIn 2000, the world population was 6.08 billion and was increasing at a rate 1.21% each year.1. Write a function for world population. Does

the function represent growth or decay?P(t) = 6.08(1.0121)t

2. Use a graph to predict the population in 2020.≈ 7.73 billion

The value of a $3000 computer decreases about 30% each year.3. Write a function for the computer’s value.

Does the function represent growth or decay?

4. Use a graph to predict the value in 4 years.V(t)≈ 3000(0.7)t

≈ $720.30

Holt Algebra 2


5. Tell whether the function shows growth or decay. Then graph.

Notes (continued)

f(x) = 8(½)x

Holt Algebra 2 7-1 Exponential Functions, Growth, and Decay exponential function baseasymptote...

Documents

Transcript of Holt Algebra 2 7-1 Exponential Functions, Growth, and Decay exponential function baseasymptote...