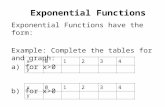
State “exponential growth” or “exponential decay” (no calculator needed)
Exponential Growth and Decay
description
Transcript of Exponential Growth and Decay

Exponential Growth and Decay
Greg Kelly, Hanford High School, Richland, Washington
Glacier National Park, MontanaPhoto by Vickie Kelly, 2004

Ex. Find the equation of the curve in the xy-plane thatpasses through the given point and whose tangent ata given point (x, y) has the given slope
2
slope = Point: (1, 1)3yx

The number of bighorn sheep in a population increases at a rate that is proportional to the number of rabbits present (at least for awhile.)
So does any population of living creatures. Other things that increase or decrease at a rate proportional to the amount present include radioactive material and money in an interest-bearing account.
If the rate of change is proportional to the amount present, the change can be modeled by:
dy kydt

dy kydt
1 dy k dty
1 dy k dty
ln y kt C
Rate of change is proportional to the amount present.
Divide both sides by y.
Integrate both sides.

1 dy k dty
ln y kt C
Integrate both sides.
Exponentiate both sides.
When multiplying like bases, add exponents. So added exponents can be written as multiplication.
ln y kt Ce e
C kty e e

ln y kt Ce e
C kty e e
Exponentiate both sides.
When multiplying like bases, add exponents. So added exponents can be written as multiplication.
C kty e e
kty Ae Since is a constant, let .Ce Ce A

C kty e e
kty Ae Since is a constant, let .Ce Ce A
At , .0t 0y y00
ky Ae
0y A
1
0kty y e This is the solution to our original initial
value problem.

0kty y eExponential Change:
If the constant k is positive then the equation represents growth. If k is negative then the equation represents decay.

Population Growth
In the spring, a bee population will grow according to an exponential model. Suppose that the rate of growth of the population is 30% per month.
a) Write a differential equation to model the population growth of the bees.
b) If the population starts in January with 20,000 bees, use your model to predict the population on June 1st.