Cap6 Frenos y Embragues
-
Upload
cristian-carvajal -
Category
Documents
-
view
105 -
download
4
Transcript of Cap6 Frenos y Embragues
-
FRENOS Y EMBRAGUES
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 87
INDICE 6. FRENOS Y EMBRAGUES ......................................................................................................................88
6.1 INTRODUCCIN ....................................................................................................................................88 6.2 ANLISIS DE UN EJEMPLO SENCILLO. ...................................................................................................89 6.3 CONSIDERACIONES ENERGTICAS. .......................................................................................................91 6.4 EMBRAGUES Y FRENOS CON ZAPATAS INTERIORES...............................................................................93 6.5 EMBRAGUES Y FRENOS DE TAMBOR CON ZAPATAS EXTERIORES. .........................................................96 6.6 EMBRAGUES Y FRENOS DE CINTA O BANDA..........................................................................................99 6.7 EMBRAGUES CNICOS DE ACCIN AXIAL. ..........................................................................................101
6.7.1 Embrague nuevo: distribucin de presiones uniforme. ................................................................102 6.7.2 Embrague usado: desgaste uniforme. ..........................................................................................103
6.8 EMBRAGUES DE DISCO DE ACCIN AXIAL...........................................................................................104 6.8.1 Embrague nuevo: distribucin uniforme. .....................................................................................105 6.8.2 Embrague usado: desgaste uniforme. ..........................................................................................106
6.9 MATERIALES DE FRICCIN. ................................................................................................................107 6.10 EJEMPLOS DE FRENOS Y EMBRAGUES .................................................................................................108
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 88
6. FRENOS Y EMBRAGUES
6.1 Introduccin Son elementos relacionados con el movimiento de rotacin: transmitir o absorber energa mecnica de rotacin. En el momento del embrague dos masas que estn girando a distintas velocidades se intentan llevar a la misma velocidad (en el caso del freno una de ellas tiene velocidad cero). Se produce un deslizamiento relativo, hay rozamiento con generacin de calor e incremento de temperatura (figura 6.1)
Figura 6.1 Representacin esquemtica de un embrague.
El anlisis de funcionamiento incluye el estudio de la fuerza ejercida, del par de rozamiento, de la energa perdiday del aumento de la temperatura. El par de rozamiento depende de:
- la fuerza ejercida. - el coeficiente de rozamiento. - la geometra de las superficies.
El mtodo de anlisis de todos los tipos de embragues y frenos de friccin es:
a) suponer la distribucin de presiones sobre las superficies de friccin. b) determinar la relacin entre la presin mxima y la presin en un punto cualquiera. c) aplicar las ecuaciones de equilibrio esttico para determinar la fuerza actuante, el
par de torsin y las reacciones en apoyos.
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 89
6.2 Anlisis de un ejemplo sencillo. Sea la zapata de la figura 6.2 articulada en un punto fijo B, de corta longitud. La fuerza F presiona el material de friccin -cuya rea es A- sobre una superficie plana que est en movimiento; f es el coeficiente de friccin.
Figura 6.2 Zapata corta actuando sobre un plano
Siguiendo los pasos antes enunciados para el anlisis a), b) y c): a) como la zapata es corta suponemos una presin uniformemente distribuida sobre
la superficie de friccin. b) llamando N a la fuerza normal al plano en movimiento, teniendo en cuenta la
hiptesis que se ha hecho en a) se calcula la presin mxima y la presin en un punto cualquiera (que en este caso coinciden):
p p NA
pi = = =max
c) para el clculo de la fuerza N se plantea el equilibrio de los elementos del freno (figura 6.3):
Figura 6.3 Equilibrio de zapata corta actuando sobre un plano
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 90
M=0 (en la articulacin):
+ + =Nb Fb fNa 0 y por tanto, ( )
FpA b fa
b=
esta ecuacin relaciona F y p, ahora bien si b=f.a entonces F=0. Se produce un
fenmeno de autotrabado del freno. Por lo general no interesa este efecto y se suele coger f'=0,75 a 0,8 del valor de f "autotrabante".
Pueden hallarse tambin las reacciones en la articulacin:
R fpAR pA
x
y F==
- Analizando este caso se pueden hacer dos comentarios: i) respecto al uso del material de friccin: p es constante, luego si se quiere hacer
un aprovechamiento mximo del material de friccin se calcular para que p=pmax.
. ii) si b=f.a, se produce frenado aunque la fuerza F=0, se habla de autotrabado.
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 91
6.3 Consideraciones energticas. Cuando se detienen los elementos rotatorios de una mquina con un freno, ste debe absorber la energa cintica de rotacin calor. De igual forma durante un deslizamiento el embrague absorbe energa calor. La capacidad de un embrague (o freno) est limitada por:
caractersticas del material de friccin. capacidad de disipacin de calor; si el calor se genera ms rpido de lo que se
disipa Temperatura.
Para tener una idea de lo que sucede en un embrague o freno, consideremos un modelo matemtico: T es el momento aplicado por el embrague que se supone constante, los ejes son rgidos, 1 y 2 son las velocidades iniciales (figura 6.4):
Figura 6.4 Esquema de un embrague
=T I1 1&& T I= 2 2&&
integrando las dos ecuaciones anteriores:
11
1 += tIT&
22
2. += tIT&
la velocidad relativa & & & = 1 2 t
IIIIT
+=
21
2121 &
de la ecuacin anterior se puede deducir el tiempo t1 para el que se produce la igualdad de velocidades ( )
( )tI I
T I I11 2 1 2
1 2
= +
Puede hallarse tambin la potencia que se est disipando en funcin de t:
( ) ( )P T T T I II I tdis = = +
.
& 1 2 1 21 2
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 92
Esta potencia es mxima para t=0 (justo en el momento en el que se produce el embraguado). La expresin anterior permite calcular la energa total disipada:
( ) ( )E P dt T T I II I
t dtdist t= = +
0 1 2
1 2
1 20
1 1
( )( )E
I I
I I= +
1 2 1 22
1 22
del anlisis de la ecuacin anterior se deduce fcilmente que la energa total disipada, E, es independiente del momento o par de tensin del embrague y proporcional al cuadrado de la diferencia de velocidades.
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 93
6.4 Embragues y frenos con zapatas interiores. En este caso se pretende estudiar el freno de la figura 6.5 siguiendo los mismos pasos que en el apartado anterior.
Figura 6.5. Freno de tambor con zapata interior
a) Zapata larga: la distribucin de las fuerzas normales no puede suponerse
constante. Se hace la hiptesis de que la presin p en un punto definido por es proporcional a la altura sobre el punto de la articulacin.
b) de la hiptesis a) se deduce por tanto que la presin p, en un punto cualquiera
definido por , se puede relacionar con el punto de presin mxima, pa, definido por a:
P Paasin sin =
la presin mxima se producir a=90 (en caso de que el material de friccin
llegue hasta este punto) y la presin es cero para =0.Un buen diseo de zapata por tanto concentrara ms material de friccin donde hay ms presin, y lo omitira en el taln (=0).
c) siendo b el ancho de la zapata, se determinar la fuerza F mediante la condicin
MA=0. Se plantea el equilibrio sabiendo que:
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 94
dN pbrd P br daa
= = sinsin
llamando Mf al momento de las fuerzas de friccin, y MN al momento de las
fuerzas normales:
M F M McA
N f= = 0
se calculan a continuacin MN y Mf:
Mf (momento de las fuerzas de friccin)
( )M fdN r af = cos
la ecuacin se integrar entre 1 y 2, puntos entre los que se encuentra el material de friccin:
(M fP brsen
sen r a dfa
a= cos12 )
( )sin cos cos sin r a d r a = 2 2
y por tanto,
MfP brsen
ra
fa
a=
(cos cos ) (sin sin )2 1
22
212
MN (momento de las fuerzas normales)
M dN aN = . .sin M
p b r adN
a
a= . .sin sin . 212
sin .sin2
22
4 d =
y por tanto,
( )M
p b r aN
a
a=
. .sin
( ) sin sin
2 1 22
2 24
1
Volviendo de nuevo a la ecuacin en la que F se relaciona con MN y Mf se observa que existe en este caso una condicin de F = 0, sera el caso en el que se dara un efecto de autotrabado del freno. En el caso que hemos estudiado se produce un efecto autoenergizante puesto que el momento de las fuerzas de rozamiento ayuda a la fuerza de frenado F. Si se invierte el sentido de la rotacin del tambor se cambia el sentido de las fuerzas de friccin y entones se pierde el efecto autoenergizante.
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 95
Puede calcularse tambin el par de frenado, T:
T f r dNfP br
daa
= = . . sin sin .2
1
2
( )T fp braa
= 2
1 2sincos cos
Para su posterior aplicacin prctica, debe tenerse en cuenta que las ecuaciones anteriores se basan en las siguientes hiptesis:
- la presin en un punto de contacto en la zapata es proporcional a la altura sobre el taln.
- el efecto de la fuerza centrfuga es despreciable. - se considera la zapata rgida y se desprecia el efecto de la deformacin. - se considera que el coeficiente de rozamiento es constante e independiente de
las condiciones de contacto (temperatura, desgaste, etc..).
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 96
6.5 Embragues y frenos de tambor con zapatas exteriores. La notacin y las hiptesis que se emplearn en este apartado son las mismas que las del apartado anterior.
Figura 6.6. Esquema de un freno con zapata exterior
Tomando momentos en la articulacin se pueden hallar las siguientes expresiones para los momentos de las fuerzas de rozamiento y las fuerzas normales:
(M fP brsen
sen r a dfa
a= cos12 )
Mp b r a
dNa
a= . .sin sin . 212
El equilibrio de la zapata (MA=0) proporciona la relacin entre estos momentos y la fuerza sobre la zapata, F:
FM M
cN= + f
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 97
Las reacciones horizontal y vertical se obtienen haciendo F=0, R dN f dNx = + cos . sin . Fx
y+
R f dN dN Fy = .cos . sin . sustituyendo,
R p br A fB Fx aa
x= +sin ( )
R p br fA B Fy aa
y= sin ( ) + donde,
A d= = sin cos . sin
1
2
1
212
2
B d= = sin .
sin21
2
1
2
22
4
Si la rotacin del tambor fuese en sentido contrario, existira autoenergizacin y la fuerza F tendra la siguiente expresin:
FM M
cN f=
Cuando se emplean elementos con zapatas exteriores como embragues el efecto de la fuerza centrfuga es reducir la fuerza normal, al aumentar , hay que aumentar F. Caso especial a estudiar es cuando la articulacin (o pivote) est situado de tal forma que el momento de las fuerzas de friccin en este punto es nulo (figura 6.7)
Figura 6.7.Freno con zapata exterior aticulada simtrica.
Se hace la hiptesis de desgaste "cilndrico", x=constante, es decir (ver figura 6.7):
r x= .cos
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 98
puesto que la presin es proporcional al desgaste radial, la relacin entre la presin en un punto cualquiera y la mxima ser:
p pa= cos La presin es mxima, pa, para =0. Pasando al anlisis de fuerzas, se elige a de modo que Mf=0. Se toma en este caso 1=2:
M fdN a rf = 2 0 2 ( cos ) = 0 puesto que,
dN p br da= cos sustituyendo, se halla el valor de a para el que Mf es nulo:
a r= +4
2 22
2 2
sinsin
Las reacciones horizontal, Rx, y vertical, Ry, tienen las siguientes expresiones:
R dNp br
Nxa= = +2 2 2 20 2 22 cos ( sin ) =
R f dNp brf
fNya= = +2 2 2 20 2 22 cos ( sin ) =
El momento de frenado (teniendo en cuenta la simetra de la zapata la deduccin es sencilla), T:
=== afNbrfprfdNT a 22 sin2
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 99
6.6 Embragues y frenos de cinta o banda. Este tipo de frenos funciona mediante una cinta o banda flexible de friccin. Se utiliza en excavadoras mecnicas, montacargas, etc. Su funcionamiento puede explicarse a partir de la figura 6.8.
Figura 6.8 Esquema de funcionamiento de un freno de cinta Debido a la friccin (y con el sentido de giro sealado en la figura), la fuerza de trabajo P2 es menor que la fuerza en el punto de retencin, P1. Planteando el equilibrio de un diferencial de cinta, F=0:
( ) sin sinP dP d P d dN+ + = 2 2
0
( ) cos cosP dP d P d fdN+ = 2 2
0
de las dos ecuaciones anteriores se deduce:
dN Pd= dP fdN = 0
sustituyendo el valor de dN en la ecuacin e integrando entre P1 yP2:
dPP
f dP
P
2
1
0 = y por tanto la relacin entre las fuerzas es:
ln PP
f PP
e f12
1
2
= = y la expresin para el par de frenada, T:
T P P r= ( 1 2 )
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 100
La presin que acta sobre la cinta, p, puede deducirse de la puesto que sobre el diferencial de longitud rd y ancho b acta una fuerza dN:
dN pbrd Pd pbrd= = y por tanto
p Pbr
= De la ecuacin anterior se deduce directamente que el punto en el que la presin es mxima es:
p Pbra
= 1
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 101
6.7 Embragues cnicos de accin axial. Los embragues se emplean para llevar dos ejes a la misma velocidad de rotacin; el efecto se produce por un par de rozamiento T. El embrague cnico es uno de los tipos de embrague ms antiguo, tan slo se emplea en aplicaciones sencillas, es simple y eficaz. Un embrague se llama de accin axial si los elementos de friccin que entran en contacto se mueven paralelamente al eje de rotacin (Figura 6.9)
Figura 6.9. Embrague cnico de accin axial
El cono puede deslizarse axialmente, un resorte mantiene la conexin (o cierre) del embrague. El embrague se desconecta (o abre) mediante un mecanismo que ajusta en la ranura de cambios. El ngulo del cono , dimetro y ancho, son los parmetros de diseo (valores normales para entre 10 y 15). Para hallar una relacin entre la fuerza de trabajo F y el momento de torsin transmitido se parte del esquema de la figura 6.10. Dos hiptesis son posibles segn se considere el embrague nuevo o usado:
a) distribucin de presiones uniforme (embrague nuevo). b) desgaste uniforme (embrague usado).
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 102
6.7.1 Embrague nuevo: distribucin de presiones uniforme.
Figura 6.10 Fuerzas actuantes en un embrague cnico
Partiendo de la figura 6.10 se puede integrar la presin en la superficie de contacto para obtener la fuerza F, se supone p=pm:
F p dA prdr
md
D
= = sin . sin sin 22
2
(F p D dm= )4
2 2
De igual forma puede deducirse el momento de torsin transmitido en funcin de pm:
T frpdA fpr dr
md
D
= = 2 22
2 sin
(T f p D dm= ) 12 3 3sin
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 103
6.7.2 Embrague usado: desgaste uniforme.
En esta hiptesis se supone que el desgaste en la direccin del eje de rotacin es constante (Figura 6.11), =constante:
Figura 6.11. Desgaste radial y axial de un embrague cnico.
El desgaste radial, r, es proporcional al trabajo de las fuerzas de rozamiento en este punto, y si queremos que el desgaste sea uniforme se tiene que cumplir que:
p r cste p p drm
. = =2
Conocida la distribucin de presiones se pueden calcular la fuerza F y el par transmitido, T:
(F p dr
rdr p dD dmd
Dm= = 2 2 2
2
2
sinsin )
(T fp dr rdrr f p d D dmdD
m= = 2 2 82
2 2 2
sin sin )
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 104
6.8 Embragues de disco de accin axial. En muchas aplicaciones los embragues de disco han desplazado a los cnicos: presentan una gran superficie de friccin en un espacio reducido, adems la superficie disipadora de calor es ms efectiva.
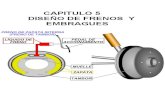
1. eje cigueal. 2. segundo eje (al cambio) 3. cojinete de friccin. 4. volante de inercia. 5. tapa (unida al volante). 6. anillo presor. 7. muelles helicoidales. 8. disco del embrague. 9. forros. 10.cubo (unido al disco) encaja con el segundo eje
Figura 6.12. Embrague de disco de accin axial.
Los muelles helicoidales (Figura 6.12) obligan al anillo presor a separase de la tapa, as el disco del embrague queda aprisionado entre los forros. En la figura 6.13 el embrague est en posicin de no transmitir el movimiento (desembragado), para ello es necesario separar del disco del embrague el anillo de presin comprimiendo los muelles (en un automvil normalmente esto se realiza mediante un pedal).
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 105
Figura 6.13 Embrague de disco en posicin desembragado
En el clculo de la relacin existente entre la fuerza de trabajo, F, y el par transmitido por rozamiento, T, se emplean las mismas hiptesis que en el apartado anterior.
6.8.1 Embrague nuevo: distribucin uniforme.
Con el embrague nuevo supondremos una distribucin uniforme de la presin en el disco. p=pm:
Figura 6.14 Esquema disco de embrague o freno
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 106
(F p dA p rdr p D dmdD m= = = .2
2 2 224
) (T frpdA fp r dr f p D dm mdD= = = 2 122
2
2 3 3 ) 6.8.2 Embrague usado: desgaste uniforme.
La hiptesis de desgaste uniforme supone:
p r cste p dm. = = 2 y por tanto,
(F p dA p dr
rdrp d
D dmdD
m= = = .2
22
22
)
(T frpdA fp dr r dr f p D dm mdD
= = = 2 2 822
2 2 2 )d
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 107
6.9 Materiales de friccin. Las propiedades de un material de friccin para freno o embrague deben ser las siguientes:
- coeficiente de friccin alto y uniforme. - propiedades poco dependientes de condiciones externas (p.ej. humedad). - buena conductividad trmica y capacidad de resistir altas temperaturas. - alta resistencia al desgaste, rayado y raspadura.
La Tabla 6.1 recoge una variedad amplia de materiales de friccin, algunos pueden trabajar en hmedo, sumergidos en aceite o rociados (esto reduce algo el coeficiente de friccin pero permite emplear presiones mayores). La Tabla 6.2 recoge algunas propiedades de revestimientos tpicos de frenos (fibras de asbesto que proporcionan fuerza y capacidad de resistir altas temperaturas, partculas de friccin y materiales aglutinantes).
Tabla 6.1 Materiales de friccin para embragues.
Tabla 6.2 Algunas propiedades de revestimientos para frenos
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 108
6.10 Ejemplos de frenos y embragues
Figura 6.15. Embrague de disco
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 109
Figura 6.16. Embrague hidrulico multidisco
-
tecnun CAMPUS TECNOLGICO UNIVERSIDAD DE NAVARRA
Frenos y Embragues
Elementos de Mquinas 110
Figura 6.17. Freno de disco para automvil
FRENOS Y EMBRAGUESIntroduccinAnlisis de un ejemplo sencillo.Consideraciones energticas.Embragues y frenos con zapatas interiores.Embragues y frenos de tambor con zapatas exteriores.Embragues y frenos de cinta o banda.Embragues cnicos de accin axial.Embrague nuevo: distribucin de presiones uniforEmbrague usado: desgaste uniforme.
Embragues de disco de accin axial.Embrague nuevo: distribucin uniforme.Embrague usado: desgaste uniforme.
Materiales de friccin.Ejemplos de frenos y embragues