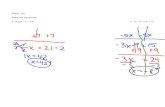– 1

FRENTE 1 – ÁLGEBRA

n Módulo 15 –Determinantes

1) = € 10 – 5x = x2 – 4 €

€ x2 + 5x – 14 = 0 € x = – 7 ou x = 2

A solução positiva, x = 2, é um número primo.

Resposta: B

2) A nova matriz obtida, de acordo com o enunciado, é

, e o determinante dessa matriz é

8 + 8 + 18 – 16 – 6 – 12 = 0

Resposta: C

3) + = €

€ x . x – 0.1 + 0.1 – y.y = x(x + 1) – y(y + 1) €€ x2 – y2 = x2 + x – y2 – y € 0 = x – y € y = xObserve que a expressão da alternativa a está correta, poistrata-se de uma soma de matrizes, porém, não é equivalenteà expressão dada no enunciado que é uma soma dedeterminantes.Resposta: E

4) = € = 1 – x €

€ (1 – x)2 = 1 – x € (1 – x)2 – (1 – x) = 0 €

€ (1 – x) . (1 – x – 1) = 0 € (1 – x) . (– x) = 0 €

€ x = 1 ou x = 0 fi x = 0, pois deve-se ter 1 – x ≠ 0 € x ≠ 1 fi

fi S = {0}

Resposta: E

5) Se a matriz A é quadrada de ordem 2 com

, então:

I) A = = =

II) det A = = 2 – (– 4) = 2 + 4 = 6

Resposta: E

6) I) A – x . B = – x . =

= – =

II) det(A – x . B) = 0 fifi (2 – 4x) . (4 + x) – (1 – 2x) . (3 – 3x) = 0 €

€ 8 + 2x – 16x – 4x2 – 3 + 3x + 6x – 6x2 = 0 €€ – 10x2 – 5x + 5 = 0 € 2x2 + x – 1 = 0 €

€ x = – 1 ou x =

Resposta: x = ou x = – 1

7) = 175 €

€ – 2x2 + 4x + 18 + 3x + 24 + 2x2 = 175 €

€ 7x + 42 = 175 € 7x = 133 € x = 19

Resposta: V = {19}

8) I) A = Bt fi = fi

fi €

II) = =

= – 4 – 10 + 4 + 10 = 0

Resposta: B

9) = 0 € (1 + a) . (1 – a) + 3 = 0 €

€ 1 – a2 + 3 = 0 € a2 = 4 € a = 2 ou a = – 2

Resposta: A

10) I) A . B = I fi . = €

€ = fi

fi €

II) Para a = 5 e b = – 1, tem-se A = =

III) det A = = – 5 + 4 = – 1

IV) det A2 = det (A . A) = det A . det A = (– 1) . (– 1) = 1Resposta: A

CADERNO 4 – CURSO E

�1x

x4��5

52x�

�134

246

112

�

�y + 1x + 1

xy��y

10y��1

xx0�

1 – x––––––1 – x�1

11x�

1 x� 1 1 �–––––––––

1 1� x 1 �

aij = 2i – j, para i = jaij = 3i – 2j, para i ≠ j�

�– 12

14��3.1 – 2.2

2.2 – 22.1 – 1

3.2 – 2.1��a12a22

a11a21

��– 1

214�

�2– 1

43��1

423�

�1 – 2x4 + x

2 – 4x3 – 3x��2x

–x4x3x��1

423�

1–––2

1–––2

�2– 21

x– x– 3

34x

�

�y– x

4z��0

y + zx2

2�x = – 2y = 0z = 2

�x2 = 4y = 0z = 2y + z = – x

��– 2

24

015

– 112

��xz4

y15

– 112

�

�– 11 – a

1 + a3�

�01

10��1

– 51

– 4��1b

a– 4�

�01

10��a – 5

– 4 – 5ba – 4

– 4 – 4b�

a = 5b = – 1�

a – 4 = 1a – 5 = 0– 4 – 4b = 0– 4 – 5b = 1

��1

– 15

– 4��1b

a– 4�

�1– 1

5– 4�

MATEMÁTICA

11) I) M + k . I = + k . =

= + =

II) det(M + k . I) = 0 fi = 0 fi

fi (2 + k) . (5 + k) + 2 = 0 € 10 + 2k + 5k + k2 + 2 = 0 €€ k2 + 7k + 12 = 0 € k = – 4 ou k = – 3

Resposta: C

n Módulo 16 –Propriedades dosDeterminantes

1) D = = – = , pois cada troca de

filas paralelas provoca a troca do sinal do valor do deter -minante. Observe que, inicialmente, trocaram de posição a 1a.e a 2a. linhas e, finalmente, trocaram de posição a 1a. e a 2a.colunas. Resposta: D

2) I) x = = , pois trata-se do determinante de

uma matriz e da sua transposta, cujos valores são iguais.

II) y = = (– 2) . 3 . = (– 2) . 3 . x = – 6x

III) = = – 6

Resposta: C

3) I) det A = 2 fi = 2 €

€ 4 . = 2 € =

II) det B = = 3 . =

= 3 . (– 1) . =

= 3 . (– 1) . = –

Resposta: D

4) Se A é uma matriz quadrada de ordem 4 e det A = – 6, então:det(2A) = x – 97 fi 24 . det A = x – 97 fifi 16 . (– 6) = x – 97 € – 96 = x – 97 € x = 1Resposta: C

5) “O determinante da matriz At (transposta de A) é igual aodeterminante da matriz A”, pode ser expressa matemati -camente por det(At) = det AResposta: D

6) D = = = 0

Resposta: E

7) = =

= a . b . = a . b . 0 = 0, pois a 2a. e a 3a. colunas são

iguais.

Resposta: A

8) = = 0, pois a 2a. e a 3a.

colunas são proporcionais.

Resposta: C

n Módulo 17 – Teorema de Laplace, Regra de Chió e Outras Propriedades

1) Na matriz A = , tem-se a23 = 1 e o seu cofator

é dado por:

A23 = (– 1)2 + 3 . = (– 1)5 . 2 = – 2

Resposta: D

2) = 0 ⇔ 4 . (– 1)1 +2 . = 0 ⇔

⇔ 4 . (– 1)3 . x . = 0 ⇔ 4 . (– 1) . x . x . 3 . = 0,

para qualquer x Œ �, pois = 0 (filas paralelas iguais)

Resposta: D

3) = 0 ⇔ 2 . (– 1)1 + 3 . = 0 ⇔

�01

10��– 1

522�

�– 15 + k

2 + k2��0

kk0��– 1

522�

�– 15 + k

2 + k2�

�ca

db��d

bca��b

dac�

�cd

ab��b

dac�

�cd

ab��– 2c

3d– 2a3b�– 6x–––––

xy––x

�444

abc

mnp

�1––2�1

11

abc

mnp

��111

abc

mnp

�

�mnp

abc

111

��mnp

abc

333

��1

11

abc

mnp

�3––2

1––2

a – bb – cc – a

b – cc – aa – b

000

a – bb – cc – a

b – cc – aa – b

c – aa – bb – c

x1x1 +

+

xyz

aaa

bbb

.(–1)

x + ay + az + a

x + by + bz + b

xyz

++

xyz

111

111

222

111

m + 1m + 2m + 3

m + 1m + 2m + 3

m + 2m + 3m + 4

m + 3m + 4m + 5

.(–1) ++

� 210

121

312�

� 20

11 �

0x2

x0

4x67

03x30

0x45

x2

x0

3x30

x45

xx0

330

145

110

110

145

110

110

145

x10

0x8

08x

0x10

00x8

2x2

log x1

008x

2 –

⇔ 2 . (– 1)4 . (x3 – 64x) = 0 ⇔ 2 . 1 . x . (x2 – 64) = 0 ⇔⇔ x = 0 ou x2 – 64 = 0 ⇔ x = 0 ou x = – 8 ou x = 8Resposta: D

4) > 0

Multiplicando a 2a., a 3a. e a 4a. coluna por 1 e somando-as à 1a.coluna, tem-se:

> 0 ⇔ (2a + 1) . > 0

Multiplicando a 1a. linha por (– 1) e somando-a às outraslinhas, tem-se:

(2a + 1) . > 0 ⇔

⇔ (2a + 1) . 1 . (– 1)1 + 1 . > 0 ⇔

⇔ (2a + 1) . 1 . 1 . [(1 – a)2 – a2] > 0 ⇔⇔ (2a + 1) . (1 – 2a + a2 – a2) > 0 ⇔

⇔ (2a + 1) . (1 – 2a) > 0 ⇔ – < a < , pois o gráfico da

função f(a) = (2a + 1) . (1 – 2a) é do tipo

Resposta: B

5) Se A e B são matrizes quadradas de ordem n, são verdadeiras

as seguintes propriedades:

I) det A = det At

II) det(A . B) = det A . det B

III) det(A2) = det(A . A) = det A . det A = (det A)2

IV) det A . det At = det A . det A = (det A)2

Não é verdadeira a afirmação det(A + B) = det A + det B

Resposta: A

6) I) A = fi det A = x2 – 4

II) B = fi det B = – x2

III) det (A . B) = 0 fi det A . det B = 0 fifi (x2 – 4) . (– x2) = 0 ⇔ x2 – 4 = 0 ou – x2 = 0 ⇔⇔ x2 = 4 ou x2 = 0 ⇔ x = – 2 ou x = 2 ou x = 0

Resposta: E

7) det(A2) = det(A . A) = det A . det A = (det A)2

Resposta: B

8) Para A = e B = , tem-se:

I) A . B = . =

II) n = det(AB) = 0, pois a 2a. e a 3a. linha são proporcionais.

III) Para n = 0, tem-se 7n = 70 = 1

Resposta: 1

9) I) A = fi det A = 1

II) B = fi det B = ad – bc

III) det(AB) = 0 fi det A . det B = 0 fifi 1 . (ad – bc) = 0 ⇔ ad – bc = 0

Resposta: C

10) = 0 ⇔ sen2x . cos x = 0 fi

fi cos x = 0, pois sen x ≠ 0 (observe que cotg x =

não existe para sen x = 0, consequentemente, o determinantedado não poderia ser calculado).

Assim, cos x = 0 ⇔ x = + n . π, n Œ �

Para 0 ≤ x ≤ 2, o menor valor de x é obtido fazendo n = 0, que

resulta x = .

Resposta: D

n Módulo 18 – Inversão de Matrizes

1) Seja M = , então:

I) det M = 4 · 1 – 3 · 1 = 1.

II) M’ = é a matriz dos cofatores.

III)––M = (M’)t ⇒ ––

M =

IV) M–1 = · M ⇒ M–1 =

Resposta: B

� 4 31 1 �

1aa0

a10a

a01a

0aa1

2a + 12a + 12a + 12a + 1

a10a

a01a

0aa1

1111

a10a

a01a

0aa1

1000

a1 – a– a0

a– a

1 – a0

0aa1

1 – a– a0

– a1 – a

0

aa1

1–––2

1–––2

� x1

4x �

� 0x

x1 �

� 1– 1

1

0– 1

1 � � 03

14

25 �

� 1– 1

1

0– 1

1 � � 03

14

25 � � 0

– 33

1– 5

5

2– 7

7 �

� 10

11 �

� ac

bd �

� – sen x00

– 8– sen x

0

– 5cotg xcos x �

cos x–––––––sen x

π––2

π––2

�1 –1–3 4�

1 –3–1 4�

�1 –3–1 4�

1––––––det M

– 3

2) Se as matrizes são inversas uma da outra, então:

A · B = I ⇒ · = ⇔

⇔ = ⇔

⇔ = ⇔

⇔ ⇔ ⇒ x + y = – + = 0.

Resposta: E

3) Seja A–1 = , então:

I) A · A–1 = I ⇒ · = ⇔

⇔ = ⇔

⇔ = ⇔

⇔ a = 1, b = 0, c = 0, d = –1, então A–1 =

II) A + A–1 = + =

III) (A + A–1)2 = · =

= =

IV) (A + A–1)3 = · =

= =

Assim, (A + A–1)3 = 8 · A

Resposta: E

4) Se M = , então:

I) det M = = 2

II) A21 = (–1)2 + 1 · = (–1)3(2 – 0) = –1 · 2 = –2

Se b = b12 for o elemento da 1.° linha e 2.° coluna matrizinversa, então:

b = b12 = = = –1

Resposta: B

5) Se A admite inversa, det A ≠ 0 ⇒ ≠ 0 ⇔

⇔ 3x + 0 + 0 – 0 – 6x2 – 0 ≠ 0 ⇔

⇔ – 6x2 + 3x ≠0 ⇔ 3x (–2x + 1) ≠ 0 ⇔ x ≠ 0 e x ≠

Resposta: E

6) I) Se B = , seja B–1 = , então:

B · B–1 = I ⇒ · = ⇔

⇔ = ⇔

⇔ = ⇔

B–1 =

II) A · B–1 = C ⇒ · = C ⇔

⇔ C = =

= =

III) A – B + C = – + =

IV) det (A – B + C) = = 18 – (–2) = 20

Resposta: B

⇔ � a = 1b = 0b – 2d = 1

⇔ �a = 1b = 0

1c = ––

21

d = – ––2

⇔ �1 0

1 1–– – ––2 2

�

� 3 2–1 2 � �

1 0

1 1–– – ––2 2

�

�1 1

3 · 1 + 2 · –– 3 · 0 + 2 · �– ––�2 2

1 1–1 · 1 + 2 · –– –1 · 0 + 2 · �– ––�2 2

�� 3 + 1 0 – 1

–1 + 1 0 – 1 � � 4 –10 –1 �

� 3 2–1 2 � � 1 0

1 –2 � � 4 –10 –1 � � 6 1

–2 3 �

� 6 1–2 3 �

�1 00 1��a b

a – 2c b – 2d�

� 1 · a + 0 · c 1 · b + 0 · d1 · a – 2c 1 · b – 2 · d � � 1 0

0 1 �

� 1 01 –2 � � a b

c d � � 1 00 1 �

� 1 01 –2 � � a b

c d �

�3 0 00 x x0 2x 1 �

1––2

A21–––––––det M

–2–––2

� 2 00 1 �

�1 2 00 –2 12 0 1 �

�102

2– 20

011

�

� 2 · 4 + 0 · 0 2 · 0 + 0 · 40 · 4 + (–2) · 0 0 · 0 + (–2) · (4) � � 8 0

0 –8 �

� 2 00 –2 � � 4 0

0 4 �

� 2 · 2 + 0 · 0 2 · 0 + 0 · (–2)0 · 2 + (–2) · 0 0 · 0 + (–2) · (–2) � � 4 0

0 4 �

� 2 00 –2 � � 2 0

0 –2 �

� 1 00 –1 � � 1 0

0 –1 � � 2 00 –2 �

� 1 00 –1 �

�1 00 1��a b

–c –d�

� 1 · a + 0 · c 1 · b + 0 · d0 · a + (–1) · c 0 · b + (–1) · d � � 1 0

0 1 �

� 1 00 –1 � � a b

c d � � 1 00 1 �

� a bc d �

�2 + 2x = 12 + 4x = 0

–1 + 2y = 0–1 + 4y = 1

�1

x = – ––2

1y = ––

2

1––2

1––2

� 2 + 2x –1 + 2y2 + 4x –1 + 4y � � 1 0

0 1 �

� 1 · 2 + 2 · x 1 · (–1) + 2 · y1 · 2 + 4 · x 1 · (–1) + 4 · y � � 1 0

0 1 �

�1 00 1��2 –1

x y��1 21 4�

4 –

7) I) A = ⇒ det A = 3

II) B–1 = 2A ⇒ det B–1 = det (2A)

Como a matriz A é quadrada de ordem 3, então:

det (2A) = 23 · det A = 8 · det A

Assim, det B–1 = 8 · det A

III) det B = = = =

Resposta: E

8) I) det A–1 = ⇔ det A = = 5

II) det A = = 5 ⇔ 3x + 2x = 5 ⇔ 5x = 5 ⇔

⇔ x = 1 ⇔ x – 1 = 0

Resposta: E

9) (X · A)t = B ⇒ [(X · A)t]t = Bt ⇒

⇒ X · A = Bt ⇒ X · A · A–1 = Bt · A–1 ⇒

⇒ X · I = Bt · A–1 ⇒ X = Bt · A–1

Resposta: B

10) a) A · B = · =

= =

⇔ A · B =

b) B · A = · =

= =

⇔ B · A =

c) AB = BA ⇒ = ⇔

⇔ ⇔

Resposta: D

FRENTE 2 – ÁLGEBRA

n Módulo 15 –Fatorial, Número Binomiale Triângulo de Pascal ouTartaglia

1) = = 21 . 20 = 420

Resposta: C

2) = = =

= 20 . 20 = 400

Resposta: D

3) = = (n + 1) . n = n2 + n

Resposta: C

4) (n + 4)! + (n + 3)! = 15 . (n + 2)! €

€ (n + 4) . (n + 3) . (n + 2)! + (n + 3) . (n + 2)! = 15 . (n + 2)! €

€ (n + 4) . (n + 3) + (n + 3) = 15 €

€ n2 + 3n + 4n + 12 + n + 3 = 15 € n2 + 8n = 0 €

€ n . (n + 8) = 0 fi n = 0, pois n ≥ – 2

Resposta: E

5) = = = 100 . 199 = 19 900

Resposta: A

6) Se 2 = 7 , podemos ter:

I) = = 0 € € fi

fi x = 1 ou x = 2

II) Para x ≥ 3, tem-se:

2 . = 7 . €

€ = €

€ = € = 7 €

€ x2 + x = 42 € x2 + x – 42 = 0 € x = 6, pois x ≥ 3

Resposta: V = {1; 2; 6}

� a bc d � � 1 2

0 1 �

� a · 1 + b · 0 a · 2 + b · 1c · 1 + d · 0 c · 2 + d · 1 �

� a 2a + bc 2c + d �

� 1 20 1 � � a b

c d �

� 1 · a + 2 · c 1 · b + 2 · d0 · a + 1 · c 0 · b + 1 · d �

� a + 2c b + 2dc d �

� a 2a + bc 2c + d � � a + 2c b + 2d

c d �

�a = a + 2c2a + b = b + 2dc = c2c + d = d

� c = 0a = d

�x –12x 3�

1–––––––det A–1

1––5

1–––––––det B–1

1––––––––8 · det A

1–––––8 · 3

1–––24

�1 2 30 –1 11 0 2

�

21!––––19!

21 . 20 . 19!––––––––––––

19!

21! – 20!–––––––––

19!21 . 20 . 19! – 20 . 19!

––––––––––––––––––––––19!

20 . 19! . (21 – 1)–––––––––––––––––

19!

(n + 1)!–––––––––(n – 1)!

(n + 1) . n . (n – 1)!–––––––––––––––––––

(n – 1)!

� 200198 � 200!

–––––––––198! . 2!

200 . 199 . 198!–––––––––––––––

198! . 2 . 1

�x + 14 � �x – 1

2 �

�x + 14 � �x – 1

2 � �x + 1 ≥ 0x – 1 ≥ 0x + 1 < 4x – 1 < 2

�x ≥ – 1x ≥ 1x < 3

(x + 1)!–––––––––4!(x – 3)!

(x – 1)!–––––––––2!(x – 3)!

2 . (x + 1) . x . (x – 1)!–––––––––––––––––––––

4 . 3 . 2 . 17 . (x – 1)!

–––––––––––2 . 1

(x + 1) . x–––––––––––

4 . 37

–––2

(x + 1) . x–––––––––––

2 . 3

– 5

7) = ≠ 0 € k = p ou k + p = n, pois se k + p = n os

números binomiais são complementares. Resposta: E

8) = ≠ 0 € 5 – x = 5x – 7 ou

5 – x + 5x – 7 = 14 € 6x = 12 ou 4x = 16 € x = 2 ou x = 4Resposta: V = {2; 4}

9)

Utilizando a Relação de Stifel, observando as duas linhas doTriângulo de Pascal acima, tem-se:

+ =

Resposta: C

10)

I) e são números binomiais complementares,

pois p + m – p = m, então, = = 55II) Utilizando a Relação de

Stifel, observando as duas linhas do Triângulo de Pascal

acima, tem-se:

+ = fi

fi 10 + = 55 € = 45

Resposta: B

11) = + + + + = 24 = 16, pois

é a soma de todos os números binomiais da linha 4.

Resposta: 16

12) = + + + + =

= 26 – – = 64 – 1 – 1 = 62

Resposta: 62

13) = + + + = = =

= = 5 . 4 = 20, pois é a soma dos primeiros

elementos da coluna 2, e o resultado localiza-se na linha

seguinte (5 + 1 = 6) e na coluna seguinte (2 + 1 = 3), em

relação ao último binomial somado.

Resposta: 20

14) = + + + + = =

= = = 7 . 5 = 35, pois é a soma dos

primeiros elementos de uma diagonal, e o resultado localiza-

se abaixo do último binomial somado.

Resposta: 35

15) = + + + … + = =

= = = 462

Resposta: 462

16) = 512 € + + + … + = 512 €

€ 2m = 29 € m = 9

Resposta: E

n Módulo 16 –Teorema do Binômio eTermo Geral

1) I) Os coeficientes da linha 4 do triângulo de Pascal são 1, 4,6, 4 e 1.

II) (x – y)4 = 1x4y0 – 4x3y1 + 6x2y2 – 4x1y3 + 1x0y4 =

= x4 – 4x3y + 6x2y2 – 4xy3 + y4

2) I) Os coeficientes da linha 6 do Triângulo de Pascal são 1, 6,

15, 20, 15, 6 e 1

II) (x – 2)6 =1x620 – 6x521 + 15x422 – 20x323 + 15x224 – 6x125 +

+ 1x026 = x6 – 12x5 + 60x4 – 160x3 + 240x2 – 192x + 64

3) I) No desenvolvimento de (x2 + 2)10, com expoentes decres -

centes de x, o termo geral é Tk + 1 = . (x2)10 – k . 2k

II) Fazendo k = 3, obtém-se o 4o. termo, assim:

T4 = . (x2)10 – 3 . 23 = 120 . x14 . 8 = 960 . x14

Resposta: 960x14

4) I) No desenvolvimento de x2 +4

, o termo geral é

Tk + 1 = . (x2)4 – k . k

= . x8 – 2k . k

II) Para obter o termo em x4, devemos ter 8 – 2k = 4 € k = 2,assim:

T3 = . x8 – 2 . 2 . 2

= 6 . x4 . = . x4

Resposta: A

� nk � � n

p �

� 145 – x � � 14

5x – 7 �

20 20 20 20 20� � � � … � � � � … � �0 1 13 14 20

21 21 21 21 21 21� � � � … � � � � … � � � �0 1 13 14 20 21

� 2013 � � 20

14 � � 2114 �

m – 1 m – 1 m – 1 m – 1 m – 1� �� �… � �� � … � �0 1 p – 1 p m – 1

m m m m m m� � � � … � � � � … � �� �0 1 p – 1 p m – 1 m

� mp � � m

m – p �

� mp � � m

m – p �

� m – 1p – 1 � � m – 1

p � � mp �

� m – 1p � � m – 1

p �

4�

k = 0� 4

k � � 40 � � 4

1 � � 42 � � 4

3 � � 44 �

5�

k = 1� 6

k � � 61 � � 6

2 � � 63 � � 6

4 � � 65 �

� 60 � � 6

6 �

5�

k = 2� k

2 � � 22 � � 3

2 � � 42 � � 5

2 � � 63 � 6!

–––––3!3!

6 . 5 . 4 . 3!––––––––––––3 . 2 . 1 . 3!

4�

k = 0�k + 2

k � � 20 � � 3

1 � � 42 � � 5

3 � � 64 � � 7

4 �7!

–––––4!3!

7 . 6 . 5 . 4!–––––––––––––4! . 3 . 2 . 1

10�

p = 4� p

4 � � 44 � � 5

4 � � 64 � � 10

4 � � 115 �

11!–––––5!6!

11 . 10 . 9 . 8 . 7 . 6!––––––––––––––––––––

5 . 4 . 3 . 2 . 1 . 6!

m�

k = 0� m

k � �m0 � � m

1 � � m2 � � m

m �

� 10k �

� 103 �

� 3–––2 �

� 4k � � 3

–––2 � � 4

k � � 3–––2 �

� 42 � � 3

–––2 � 9

–––4

27––––

2

6 –

5) I) No desenvolvimento de x2 +12

, o termo geral é

Tk + 1 = . (x2)12 – k . (x–3)k = . x24 – 2k . x– 3k =

= . x24 – 5k

II) Para obter o termo em x2, devemos ter 24 – 5k = 2 €

€ k = , assim, não existe o termo pedido, pois k œ �.

Observe que k deve ser um número natural entre 0 e 12

para que se tenha o binomial ≠ 0

Resposta: não existe

6) I) No desenvolvimento de x +8

, o termo geral é

Tk + 1 = . x8 – k . k

= . x8 – k . 4k . 3– k . x– k =

= . 4k . 3– k . x8 – 2k

II) Para obter o termo independente de x, isto é, o termo comx0, devemos ter 8 – 2k = 0 € k = 4, assim, o termo é Tk + 1 = T5 (5o. termo)

Resposta: D

7) A soma dos coeficientes do desenvolvimento de (3x + 2y)5 éobtida fazendo x = 1 e y = 1, assim:S = (3 . 1 + 2 . 1)5 = (3 + 2)5 = 55 = 3125

Resposta: 3125

8) A soma dos coeficientes do desenvolvimento de (x – y)104 é

obtida fazendo x = 1 e y = 1, assim:

S = (1 – 1)104 = 0104 = 0

Resposta: C

n Módulo 17 – Arranjos Simples ePermutações Simples

1) Já que os livros são diferentes, o número de maneiras dedistribuir esses livros é A42,2 = 42 . 41 = 1722Resposta: B

2) Existem 10 maneiras para escolher o coordenador, 9maneiras para o secretário e 8 para o digitador, assim, onúmero de equipes é 10 . 9 . 8 = 720 ou A10; 3 = 10 . 9 . 8 =720Resposta: E

3) Números de 3 algarismos são do tipo .

Dispondo dos algarismos de 0 a 9, sem repetição, para formarnúmeros maiores que 500, o número de possibilidades é:I) 5 para C (5, 6, 7, 8 ou 9)II) 9 para D (deve ser diferente de C)III) 8 para U (deve ser diferente de C e de D)Assim, a quantidade pedida é 5 . 9 . 8 = 360Resposta: 360

4) Números de 4 algarismos são do tipo .

Dispondo dos algarismos de 0 a 9, sem repetição, para formarnúmeros ímpares, o número de possibilidades é:I) 5 para U (1, 3, 5, 7 ou 9)II) 8 para M (deve ser diferente de U e diferente de zero)III) 8 para C (deve ser diferente de U e de M)IV) 7 para D (deve ser diferente de U, de M e de C)Assim, a quantidade pedida é 5 . 8 . 8 . 7 = 2240Resposta: 2240

5) Números de 4 algarismos são do tipo .

Dispondo dos algarismos de 0 a 9, sem repetição, para formarnúmeros pares, existem duas situações:I) Se o número terminar com zero, o número de possibili -

dades é 9 para M, 8 para C e 7 para D, totalizando 9 . 8 . 7 = 504.

II) Se o número não terminar com zero, o número de possi -bilidades é 4 para U (2, 4, 6 ou 8), 8 para M (deve serdiferente de U e diferente de zero), 8 para C e 7 para D,totalizando 4 . 8 . 8 . 7 = 1792

Assim, a quantidade pedida é 504 + 1792 = 2296Resposta: 2296

6) Dispondo dos algarismos 1, 2, 3 e 4, sem repetição, podemser formados:I) Números com 1 algarismo, num total de 4II) Números com 2 algarismos, num total de 4 . 3 = 12III) Números com 3 algarismos, num total de 4 . 3 . 2 = 24IV) Números com 4 algarismos, num total de 4 . 3 . 2 . 1 = 24Assim, a quantidade pedida é 4 + 12 + 24 + 24 = 64Resposta: E

7) Com 14 clubes de futebol, o número de possibilidades paraescolher o time que joga no seu campo é 14 e o número demaneiras para escolher o seu adversário é 13. Assim, o totalde jogos é 14 . 13 = 182 ou A14,2 = 14 . 13 = 182Resposta: 182

8) A palavra VESTIBULAR tem 10 letras, assim, o número deanagramas é P10 = 10! = 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 =3 628800

Resposta: 3 628 800

Questões 9 a 16:A palavra ALIMENTO tem 8 letras.

9) O número de anagramas que começam com M éP7 = 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040Resposta: 5040

10) O número de anagramas que terminam com O éP7 = 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040Resposta: 5040

11) O número de anagramas que começam com M e terminamcom L é P6 = 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720Resposta: 720

� 1–––x3 �

� 12k � � 12

k �

� 12k �

22–––5

� 12k �

� 4–––3x �

� 8k � � 4

–––3x � � 8

k �

� 8k �

C D U

M C D U

M C D U

– 7

12) O número de anagramas que começam com uma vogal é 4 . P7 = 4 . 7! = 4 . 5040 = 20 160Resposta: 20 160

13) O número de anagramas que terminam com uma consoanteé 4 . P7 = 4 . 7! = 4 . 5040 = 20 160Resposta: 20 160

14) O número de anagramas que começam com vogal eterminam com consoante é 4 . 4 . P6 = 4 . 4 . 6! = 4 . 4 . 720 =11520Resposta: 11520

15) O número de anagramas que começam e terminam comvogal é 4 . 3 . P6 = 4 . 3 . 6! = 4 . 3 . 720 = 8640Resposta: 8640

16) I) Começam com vogal, 20160 anagramas (Ex. 40).II) Terminam em consoante, 20160 anagramas (Ex. 41).III) Começam com vogal e terminal em consoante, 11520

anagramas (ex. 42).IV) Começam com vogal ou terminam em consoante, um

total de 20160 + 20160 – 11520 = 28 800 anagramas.Resposta: 28 800

17) Dos 6 vagões do trem, um deles é o restaurante, assim, apósa locomotiva deve ser colocado um dos outros 5 vagões. Paraas demais posições não há restrições, logo, pode-se permutaros 4 vagões restantes com o restaurante. Portanto, o númerode maneiras de montar a composição é 5 . P5 = 5 . 5! = 5 . 120 = 600Resposta: D

18) Existem 3 formas de escolher o banco em que a família Souzairá sentar e P3 formas de posicioná-la nesse banco.Existem 2 formas de escolher, entre os bancos que so braram,aquele em que o casal Lúcia e Mauro senta. Para cada umdesses bancos existem duas formas de posicionar o casal (àesquerda ou à direita do banco, por exemplo) e, para cadauma dessas formas, P2 maneiras de o casal trocar de lugarentre si.Existem P4 formas de posicionar as quatro outras pessoas.Assim, no total, temos:3 . P3 . 2 . 2 . P2 . P4 = 12 . 3! . 2! . 4! = 3456 maneiras distintasde dispor os passageiros no lotação.Resposta: E

n Módulo 18 –Combinações Simples,Permutações, Arranjos eCombinações comRepetição

1) Como não importa a ordem dos livros escolhidos, o número

procurado é dado por C8,3 = = = = 56

Resposta: 56

2) C7,3 = = = = 35

Resposta: 35

3) C21,2 = = = = 210

Resposta: 210

4) C21,3 = = = = 1330

Resposta: 1330

5) I) Dos 12 brinquedos, a criança mais nova deve ganhar 5, eo número de maneiras de escolhê-los é C12,5.

II) Dos 7 brinquedos restantes, deve-se escolher 4 para acriança mais velha, num total de C7,4 maneiras.

III) Os 3 brinquedos restantes ficarão com a outra criança.Assim, o número de maneiras de distribuir os 12 brinquedos é

C12,5 . C7,4 = . = = =

= . = 792 . 35 = 27720

Resposta: 27720

6) Para comissões de 5 pessoas com, necessariamente, 2médicos, devem-se escolher, portanto, 3 enfermeiros entreos 6 existentes. O número de maneiras de escolhê-los é

C6,3 = = = 20

Resposta: C

7) I) Todos os júris de 7 pessoas tem pelo menos umadvogado.

II) O número de formas de compor o júri é

C10,7 = = = 120

Resposta: A

8) Dos 7 professores especializados em Parasitologia, devemser escolhidos 4 e, dos 4 especializados em Microbiologia,devem ser escolhidos 2. Assim, o número de equipesdiderentes que poderão ser formadas é

C7,4 . C4,2 = . = . = 35 . 6 = 210

Resposta: 210

9) Temos apenas 4 salgadinhos que são servidos quentes e os 6 restantes são servidos frios.Se a travessa deve ter exatamente 2 salgadinhos frios e só 2 quentes então o número total de possibilidades de comporessa travessa é:

C4,2 . C6,2 = . = = 90

Resposta: A

8� �3

8!–––––––3! . 5!

8 . 7 . 6––––––––3 . 2 . 1

7� �3

7!–––––––3! . 4!

7 . 6 . 5––––––––3 . 2 . 1

21� �2

21!–––––––2! . 19!

21 . 20––––––––

2 . 1

21� �3

21!–––––––3! . 18!

21 . 20 . 19–––––––––––

3 . 2 . 1

12� �57� �4

12!–––––––5! . 7!

7!–––––––4! . 3!

12 . 11 . 10 . 9 . 8–––––––––––––––––––

5 . 4 . 3 . 2 . 1

7 . 6 . 5–––––––––3 . 2 . 1

6� �3

6 . 5 . 4–––––––––3 . 2 . 1

10!––––––7!3!

10 . 9 . 8––––––––

6

7� �44� �2

7 . 6 . 5–––––––––3 . 2 . 1

4 . 3––––––2 . 1

6 . 5 . 4 . 3 . 2 . 1–––––––––––––––

2 . 2. 2

6!–––––2! 4!

4!–––––2! 2!

8 –

10) Existem 3 possibilidades:I) A comissão é formada por 1 especialista e 2 outros

profissionais. Assim, tem-se: C3,1 . C9,2 = 3 . 36 = 108II) A comissão é formada por 2 especialistas e 1 outro

profissional. Assim, tem-se: C3,2 . C9,1 = 3 . 9 = 27III) A comissão é formada por 3 especialistas. Assim, tem-se:

C3,3 = 1O total de comissões possíveis de se formar é: 108 + 27 + 1 = 136Resposta: D

11) P6

(3A,2R) = = = 60

Resposta: 60

12) I) O número total de permutações da palavra economia é P82.

II) O número de permutações que começam com O é P7. O

número das que terminam em O também é P7.

III) O número de permutações que começam e terminam com

O é P6.

IV) O número de permutações pedidas é P82 – 2 . P7 + P6 =

10800

Resposta: E

13) Sejam L, L as duas letras iguais e L1, L2, L3, ... Ln–2 as outrasn – 2. Se as duas letras iguais devem ficar juntas entãodevemos calcular as permutações de n – 1 elementos, pois asduas letras iguais valem por uma única letra.

L1, L2, L3, �LL , L4, ... Ln–2

n – 1

Assim sendo:(n – 1)! = 120 € (n – 1)! = 1.2.3.4.5 € (n – 1)! = 5! €€ n – 1 = 5 € n = 6Resposta: C

14) Lembrando que o primeiro algarismo deve ser diferente dezero, a quantidde de números de 3 algarismos existentes nosistema decimal de numeração é 9 . 10 . 10 = 900Resposta: 900

15) Lembrando que o primeiro algarismo deve ser diferente dezero, com os algarismos 0, 1, 2, 3 e 4, a quantidade denúmeros de 3 algarismos é 4 . 5 . 5 = 100 Resposta: 100

16) I) A quantidade total de números de 4 algarismos é 9 . 10 . 10 . 10 = 9000

II) A quantidade de números de 4 algarismos distintos é 9 . 9 . 8 . 7 = 4536

III) A quantidade de números de 4 algarismos com pelomenos dois algarismos iguais é 9000 – 4536 = 4464

Resposta: 4464

17) Devem-se escolher 5 frutas entre os 3 tipos disponíveis(maçãs, peras e laranjas), independente da ordem da escolha,assim, obrigatoriamente tem-se alguma repetição.Trata-se, portanto de combinações completas de 3 elementosem grupos de 5. Assim, o número de tipos de pacotes é dado

por C*3,5 = C3 + 5 – 1,5 = C7,5 = = = 21

Pode-se pensar em obter o número de soluções inteiras nãonegativas da equação m + p + � = 5, que é dado por

P7

(5�, 2+) = = = 21

Resposta: 21

18) I) O número de comissões diferentes, de 2 pessoas cada,que po demos formar com os n diretores de uma firma éCn,2.

Logo: Cn,2 = k € = k € n . (n – 1) = 2k

II) Se, ao formar estas comissões, tivermos que indicar umadas pessoas para presidente e a outra para suplente entãoo número de comissões será An,2 e portanto:An, 2 = k + 3 € n . (n – 1) = k + 3

III) De (a) e (b), temos: 2k = k + 3 € k = 3

IV) � fi n (n – 1) = 6 € n = 3

Resposta: A

FRENTE 3 – GEOMETRIA PLANA E ANALÍTICA

n Módulo 15 –Razão Entre as Áreas deFiguras Semelhantes e Áreados Polígonos Regulares

1) I) A área do quadrado ABCD, em cm2, é S1 = 122 = 144

II) AE = AF = = 4, em cm.

III) A área do triângulo AEF, em cm2, é

S2 = = = 8

IV) A área S do octógono, em centímetros quadrados, é:

S = S1 – 4 . S2 = 144 – 4 . 8 = 144 – 32 = 112

Resposta: D

2)

12––––

3

4 . 4–––––

2AE . AF––––––––

2

6!–––––––3! . 2!

6 . 5 . 4––––––––

2 . 1

7� �5

7 . 6––––––2 . 1

7!––––––5! . 2!

7 . 6––––––2 . 1

n!–––––––––2!(n – 2)!

n . (n – 1) = 2kk = 3

– 9

I) Se a é a área de cada um dos 6 triângulos equiláteros que

formam o hexágono central de área k, então, k = 6a.

II) A soma das áreas dos triângulos ACE e BDF é

9a + 9a = 18a = 3 . 6a = 3k

Resposta: C

3)

O pentágono hachurado tem área S correspondente a dois

triângulos equiláteros de lado 1, assim, tem-se:

S = 2 . =

Resposta: E

4)

I) � = 2 fi R = = = �3

II) S = 12 . – π . R2 = 12 . – 3 . (�3 )2 =

= 12 . �3 – 3 . 3 = 3 . (4 . �3 – 3)

Resposta: B

5)

I) SHEX = 6 . SOAB fi 6 = 6 . SOAB € SOAB = 1

II) SABC = = = SOAB = 1

Resposta: A

6)

I) SHEX = 6 . SOAB fi 2 = 6 . SOAB € SOAB = =

II) SABC = = = SOAB =

III) SPENT = SHEX – SABC = 2 – =

Resposta: E

7)

22 . �3––––––––

4

�2 . �3––––––––

4

2 . SOAB––––––––––

2

SOAB + SOBC–––––––––––––

2

1–––3

2–––6

1–––3

2 . SOAB––––––––––

2

SOAB + SOBC–––––––––––––

2

5–––3

1–––3

2�3–––––

2

��3–––––

2

�3––––

2

12 . �3––––––––

4

10 –

I) AH = HC = fi AC = 2 . = a . �3

II) SABC = = = SOAB =

III) SACM = =

IV) SABCM = . SHEX fi SABC + SACM = . SHEX fi

fi + = . 6 . €

€ + = € 2a + 4x = 3a € 4x = a € x =

V) Utilizando o Teorema de Pitágoras no triângulo ACM, temos:

(AM)2 = (AC)2 + x2 = (a . �3)2 +

2

=3a2 + = fi

fi AM =

Resposta: B

8) I) O polígono regular de n lados é formado por n triângulosisósceles congruentes, como o da figura a seguir:

II) Pelo Teorema de Pitágoras, tem-se:2

+ a2 = r2 €

2

= r2 – a2 fi

fi = � r2 – a2 € b = 2 . � r2 – a2

III) A área do polígono de n lados é dada por

n . = n . = na� r2 – a2

Resposta: C

9) Sendo R o raio do círculo maior (figura I)

e r o raio de cada círculo menor (figura II), tem-se:

I) 2 . π . R = 3 . 2 . π . r € R = 3 . r

II) s = π . r2

III) S = π . R2 = π . (3 . r)2 = π . 9 . r2 = 9 . π . r2 = 9 . s

Resposta: E

10)

I) fi

fi—MN //

—CD e MN = =

II) A área do triângulo BCD é A =

III) A área do triângulo MNP é = =

= = = . = . A

Resposta: C

11) I) SABC = 2 . SADE € = 2

II) Se a razão de semelhança entre duas figuras semelhantes

é k, a razão entre as áreas dessas figuras é k2, então:

= 2

fi 2 = 2

fi = �2

Resposta: D

�b–––2��b

–––2�b

–––2

2 . � r2 – a2 . a––––––––––––––––

2

b . a–––––

2

M é ponto médio de —BC

N é ponto médio de —BD�

b–––2

CD––––

2

b . h–––––

2

b h––– . –––

2 2–––––––––––

2

hMN . –––

2–––––––––––

2

1–––4

b . h–––––

21

–––4

b . h–––––

8

b . h–––––

4––––––––

2

SABC–––––––SADE

BC–––––DE�BC

–––––DE��BC

–––––DE�

SABC–––––––SADE

49a2–––––

16

a2–––16�a

–––4�

7a––––

4

a . �3–––––––

2

a . �3–––––––

2

a2 . �3–––––––

4

2 . SOAB–––––––––

2

SOAB + SOBC–––––––––––––

2

x . a . �3––––––––––

2

x . AC––––––––

2

1–––4

1–––4

a2 . �3–––––––

4

1–––4

x . a . �3––––––––––

2

a2 . �3–––––––

4

a–––4

3a––––

8

x–––2

a–––4

– 11

n Módulo 16 –Coordenadas Cartesianas Ortogonais e Razão deSecção

1)

2) Para que os pontos A(a; 3) e B(– 2; b) sejam coincidentes, os pares ordenados devem ser iguais, portanto, (a; 3) = (– 2; b) ⇔ a = – 2 e b = 3Resposta: a = – 2 e b = 3

3) a) b = 0; b) a = 0;c) a > 0 e b < 0; d) a = – b

4) Se a < 0 e b > 0, então:I) P(a; – b) pertence ao 3o. quadrante, pois a < 0 e – b < 0II) Q(b; – a) pertence ao 1o. quadrante, pois b > 0 e – a > 0Resposta: D

5) I) Se o ponto A(a – 3; 5) pertence à bissetriz dos quadrantesímpares, então, a – 3 = 5 ⇔ a = 8

II) Se o ponto B(4; 2b) pertence à bissetriz dos quadrantespares, então, 4 = – 2b ⇔ b = – 2

Resposta: a = 8 e b = – 2

6) a) reta paralela ao eixo das ordenadas (eixo y)b) reta paralela ao eixo das abscissas (eixo x)

7)

8) Representando graficamente os pontos (0; 0), (a; 0), (a; b) e (0; b), com a > b > 0, tem-se:

Ligando os pontos, na ordem dada, por linhas retas, forma-se

um retângulo de área a . b, cujo centro é o ponto ;

Resposta: retângulo; (a . b) u.a.; ;

9) De acordo com o enunciado, tem-se a figura a seguir.

Sendo � = 1 a medida do lado do triângulo equilátero ABC,tem-se, para o vértice C:

I) xC = =

II) yC = = =

Resposta: B

10) Observando que o quadrilátero da figura é um paralelogramode base b = 4 e altura h = 5, sua área é dada por b . h = 4 . 5 =20, em unidades de área. Resposta: C

11) 1) É falsa, pois pontos de abscissa nula estão no eixo Oy.2) É verdadeira.3) É verdadeira.4) É verdadeira.5) É falsa, pois os pontos da bissetriz dos quadrantes pares

são do tipo (a; – a)Resposta: 2, 3 e 4

�b–––2

a–––2�

�b–––2

a–––2�

1–––2

�–––2

�3––––

21�3–––––

2��3

–––––2

12 –

12) AB = � (5 – 4)2 + (0 – 3)2 = � 1 + 9 = �10

AC = � (0 – 4)2 + (4 – 3)2 = � 16 + 1 = �17

AD = � (2 – 4)2 + (–3 – 3)2 = � 4 + 36 = �40 = 2�10

BE = � (–4 – 5)2 + (2 – 0)2 = � 81 + 4 = �85

BF = | 5 – 0 | = 5

CD = � (2 – 0)2 + (–3 – 4)2 = � 4 + 49 = �53

CG = � (– 6 – 0)2 + (– 4 – 4)2 = � 36 + 64 = 10

DE = � (– 4 – 2)2 + (2 + 3)2 = � 36 + 25 = �61

EF = � (0 + 4)2 + (0 – 2)2 = � 16 + 4 = �20 = 2�5

Resposta: AB = �10 ; AC = �17; AD = 2�10; BE = �85;

BF = 5; CD = �53; CG = 10; DE = �61 ; EF = 2�5

13) De acordo com o enunciado, temos a figura a seguir:

Existem duas possibilidades para o quadrado ABCD, assim,tem-se:

I) Se o centro do quadrado for o ponto (1; 1), a distância à

origem (0; 0) é � (1 – 0)2 + (1 – 0)2 = �2

II) Se o centro do quadrado for o ponto (2; 2), a distância à

origem (0; 0) é �(2 – 0)2 + (2 – 0)2 = �8 = 2�2Resposta: E

14) Sendo P(x; – 8), Q(3; 0) e PQ = 8, tem-se:

PQ = � (x – 3)2 + (– 8 – 0)2 ⇒ 8 = � (x – 3)2 + 64 ⇒⇒ 64 = (x – 3)2 + 64 ⇔ (x – 3)2 = 0 ⇔ x – 3 = 0 ⇔ x = 3

Resposta: C

15) Se P(–1; a) pertence ao 2.° quadrante, então a � 0, assim,

sendo Q(a; – 2) e PQ = 5, tem-se:

PQ = � (a + 1)2 + (a + 2)2 = 5 ⇒ (a + 1)2 + (a + 2)2 = 25 ⇔⇔ a2 + 2a + 1 + a2 + 4a + 4 = 25 ⇔ 2a2 + 6a – 20 = 0 ⇔⇔ a2 + 3a – 10 = 0 ⇔ a – 5 ou a = 2 ⇒ a = 2, pois a � 0

Resposta: E

16) Para os pontos A(3; 4), B(– 2; 4) e C(2; 2), tem-se:

I) AB = � (3 + 2)2 + (4 – 4)2 = �25 = 5

II) AC = � (3 – 2)2 + (4 – 2)2 = � 1 + 4 = �5

III) BC = � (2 + 2)2 + (4 – 2)2 = � 16 + 4 = �20 = 2�5

V) O perímetro do triângulo ABC é AB + AC + BC =

= 5 + �5 + 2�5 = 5 + 3�5

Resposta: 5 + 3�5

17) Para os pontos A(5; 10), B(11; 2) e C(8; 11), tem-se:

I) AB = � (11 – 5)2 + (10 – 2)2 = � 36 + 64 = � 100 = 10

II) AC = � (8 – 5)2 + (11 – 10)2 = � 9 + 1 = �10

III) BC = � (11 – 8)2 + (11 – 2)2 = � 9 + 81 = �90

IV)Como AB2 = AC2 + BC2, tem-se que o triângulo ABC é

retângulo com catetos AC e BC, assim, sua área é da por

= = = = 15

Respostas: Triângulo retângulo; 15u.a.

18) Para os pontos A(0; 1), B(3; 5), C(7; 2) e D(4; – 2), tem-se:

I) AB = � (3 – 0)2 + (5 – 1)2 = � 32 + 42 = 5

II) BC = � (7 – 3)2 + (5 – 2)2 = � 42 + 32 = 5

III) CD = � (7 – 4)2 + (2 + 2)2 = � 32 + 42 = 5

IV) DA = � (4 – 0)2 + (1 + 2)2 = � 42 + 32 = 5

V) AC = � (7 – 0)2 + (2 – 1)2 = � 72 + 12 = �50

VI) BD = � (4 – 3)2 + (5 + 2)2 = � 12 + 72 = �50

VII) Como AB = BC = CD = DA (lados congruentes) e AC =

BD (diagonais congruentes), tem-se que o quadrilátero

ABCD é um quadrado.

Resposta: Quadrado

19) Para os pontos A(2; – 2), B(– 3; – 1) e C(1; 6), tem-se:

I) D = = – 2 – 2 – 18 + 1 – 12 + 6 = – 27 ≠ 0,

assim, os pontos A, B e C não estão alinhados, portanto,

são vértices de um triângulo.

II) AB = � (2 + 3)2 + (– 1 + 2)2 = � 25 + 1 = �26

III) AC = � (2 – 1)2 + (6 + 2)2 = � 1 + 64 = �65

IV)BC = � (1 + 3)2 + (6 + 1)2 = � 16 + 49 = �65

V) Como AC = BC ≠ AB, tem-se que o triângulo ABC é

isósceles e não equilátero.

Resposta: C

3 . 10–––––––

2

�10 . 3�10––––––––––––

2

�10 . �90–––––––––––

2

AC . BC–––––––

2

2– 31

– 2– 16

111

– 13

20) Para A(– 3; 6) e P(3; y), tem-se:

AP = 10 ⇒ � (3 + 3)2 + (y – 6)2 = 10 ⇔

⇔ � 36 + (y – 6)2 = 10 ⇒ 36 + (y – 6)2 = 100 ⇔

⇔ (y – 6)2 = 64 ⇔ y – 6 = – 8 ou y – 6 = 8 ⇔

⇔ y = – 2 ou y = 14 ⇒ P(3; – 2) ou P(3; 14)

Resposta: P(3; – 2) ou P(3; 14)

21) Se P(x; y) é o ponto equidistante da origem O(0; 0) e dospontos A(1; 0) e B(0; 3), então:

⇒ ⇒

⇒ ⇔ ⇔

⇔ ⇔ ⇔ ⇒ P ;

Resposta: P ;

22) Se P(x; y) é o ponto equidistante dos pontos A(0; 0), B(1; 7) e

C(7; – 1), então:

⇒ ⇒

⇒ ⇔ ⇔

⇔ ⇔ ⇔ ⇔

⇔ ⇒ P(4; 3)

Resposta: P(4; 3)

23) Sendo M o ponto médio de AB e, sendo d, a distância entre oportão e o ponto médio de AB, temos:

M = = (3;5) e d = � (3 – 3)2 + (9 – 5)2 = 4

Resposta: D

24) Se M(2; 3) é o ponto médio do segmento AB com A(5; 2) e

B(xB; yB), então:

⇔ ⇒ B(– 1; 4)

Resposta: E

25) Se (2; 5) é o ponto médio do segmento de extremos (5; y) e (x; 7),

então:

⇔ ⇒ x + y = – 1 + 3 = 2

Resposta: B

26) O centro C(– 4; 1) da circunferência é o ponto médio dodiâme tro de extremos P(2; 6) e Q(xQ; yQ), então:

⇔ ⇒ Q(– 10; – 4)

Resposta: Q(– 10; – 4)

27) No triângulo de vértices A(3; 8), B(2; – 1) e C(6; – 3), tem-se:

I) O ponto médio do lado BC é M ; = M(4; – 2)

II) O comprimento da mediana AM é dado por

AM = � (3 – 4)2 + (8 + 2)2 = � 1 + 100 = � 101Resposta: E

28) No triângulo de vértices A(1; 1), B(3; – 4) e C(– 5; 2), tem-se:

I) O ponto médio do lado AC é

M ; = M – 2;

II) O comprimento da mediana BM é dado por

BM = (3 + 2)2 + – 4 –2

= 25 + =

= =

Resposta: D

29) No triângulo de vértices A(0; 0), B(3; 7) e C(5; – 1), tem-se:

I) O ponto médio do lado BC é M ; = M(4; 3)

II) O comprimento da mediana AM é dado por

AM = � (4 – 0)2 + (3 – 0)2 = � 16 + 9 = �25 = 5

Resposta: AM = 5

30) Sendo A(– 3; 5), B(1; 7), C(xC; yC) e D(xD; yD) os vértices de umparalelogramo e sendo P(1; 1) o ponto médio das diagonais,tem-se:

I) ⇔ ⇔ ⇒ C(5; – 3)

II) ⇔ ⇔ ⇒ D(1; – 5)

Resposta: (5; – 3) e (1; – 5)

x2 + y2 – 6y + 9 = x2 + y2

x2 – 2x + 1 + y2 = x2 + y2�x2 + (y – 3)2 = x2 + y2

(x – 1)2 + y2 = x2 + y2�

�3–––2

1–––2�

3y = ––

2

1x = ––

2�6y = 9

2x = 1�– 6y + 9 = 0

– 2x + 1 = 0��3

–––2

1–––2�

� x2 + y2 = � (x – 1)2 + (y – 7)2

� x2 + y2 = � (x – 7)2 + (y + 1)2�PA = PB

PA = PC�2x + 14y = 50

14x – 2y = 50�x2 + y2 = x2 – 2x + 1 + y2 – 14y + 49

x2 + y2 = x2 – 14x + 49 + y2 + 2y + 1�x + 7y = 25

50x = 200�x + 7y = 25

49x – 7y = 175�x + 7y = 25

7x – y = 25�y = 3

x = 4�

2 + 4 2 + 8�––––––; ––––––�2 2

xB = – 1yB = 4�

5 + xB––––––– = 22

2 + yB––––––– = 32

�

x = – 1y = 3�

5 + x–––––– = 2

2

y + 7–––––– = 5

2�

xQ = – 10yQ = – 4�

2 + xQ––––––– = – 42

6 + yQ––––––– = 12

�

�– 1 – 3––––––

22 + 6

––––––2�

�3–––2��1 + 2

––––––2

1 – 5––––––

2�

121–––4�3

––2�

�221––––––

2221––––

4

�7 – 1––––––

23 + 5

––––––2�

� x2 + (y – 3)2 = � x2 + y2

� (x – 1)2 + y2 = � x2 + y2�PB = PO

PA = PO�

xC = 5yC = – 3�

– 3 + xC–––––––– = 12

5 + yC–––––––– = 12

�xA + xC–––––––– = xP2

yA + yC–––––––– = yP2�

xD = 1yD = – 5�

1 + xD–––––––– = 12

7 + yD–––––––– = 12

�xB + xD–––––––– = xP2

yB + yD–––––––– = yP2�

14 –

31) Representando os pontos dados num sistema cartesiano,tem-se a figura a seguir.

O ponto médio da diagonal AC é M(5; 0) que coincide com oponto médio da diagonal BD, assim:

⇔ ⇔ ⇒ D(9; – 3)

Resposta: A

n Módulo 17 –Alinhamento de TrêsPontos e Curvas

1) Para os pontos A(4; – 1), B(8; 1) e C(– 2; – 4), tem-se:

D = = 4 + 2 – 32 + 2 + 8 + 16 = 0, assim, os

pontos A, B e C são alinhados.Resposta: Sim

2) Para os pontos A(– 3; – 2), B(5; 2) e C(9; 4), tem-se:

D = = – 6 – 18 + 20 – 18 + 12 + 10 = 0, assim, os

pontos A, B e C são colineares.Resposta: A

3) Representando os pontos dados num sistema cartesiano,tem-se a figura a seguir:

Se o ponto P(3; m) pertence a um dos lados do triângulo ABC,observa-se que esse lado é AC, assim, A, P e C devem estaralinhados, portanto:

= 0 ⇔ m + 10 – 12 – 5m + 4 – 6 = 0 ⇔

⇔ – 4m = 4 ⇔ m = – 1Resposta: A

4) Para que os pontos A(0; a), B(a; – 4) e C(1; 2) sejam vérticesde um triângulo, deve-se ter:

≠ 0 ⇔ a + 2a + 4 – a2 ≠ 0 ⇔ a2 – 3a – 4 ≠ 0 ⇔

⇔ a ≠ – 1 e a ≠ 4Resposta: D

5) I) P(x0; y0), A(– 1; – 2) e B(2; 1) estão alinhados, então:

= 0 ⇔ – 2x0 + 2y0 – 1 + 4 – x0 + y0 = 0 ⇔

⇔ – 3x0 + 3y0 + 3 = 0

II) P(x0; y0), C(– 2; 1) e D(1; – 4) estão alinhados, então:

= 0 ⇔ x0 + y0 + 8 – 1 + 4x0 + 2y0 = 0 ⇔

⇔ 5x0 + 3y0 + 7 = 0

III) ⇔ ⇔

⇔ ⇔ ⇔

⇔ ⇒ P ; –

Resposta: P – ; –

6) Para os pontos A(0; 2), B(4; 0) e C(– 1; – 2), tem-se:

I) D = = – 2 – 8 – 8 = – 18

II) A área do triângulo ABC é dada por

S = = = = 9

Resposta: C

xD = 9yD = – 3�

1 + xD––––––– = 52

3 + yD––––––– = 02

�xB + xD–––––––– = xM2

yB + yD–––––––– = yM2�

48

– 2

– 11

– 4

111

– 359

– 224

111

135

2m– 4

111

0a1

a– 42

111

x0– 12

y0– 21

111

x0– 21

y01

– 4

111

3x0 – 3y0 – 3 = 05x0 + 3y0 + 7 = 0�– 3x0 + 3y0 + 3 = 0

5x0 + 3y0 + 7 = 0�x0 – y0 – 1 = 0

1x0 = – ––

2�x0 – y0 – 1 = 0

8x0 + 4 = 0�

�3––2

1––2�

3y0 = – ––

21

x0 = – ––2

��3

––2

1––2�

04

– 1

20

– 2

111

18––2

| – 18 |–––––––

2| D |––––

2

– 15

7) I) Se B é o ponto em que a reta x + y = 1 encontra o eixo x,

então yB = 0, logo, xB + 0 = 1 ⇔ xB = 1, portanto, B(1; 0)

II) Se C é o ponto em que a reta x + y = 1 encontra o eixo y,

então xC = 0, logo, 0 + yC = 1 ⇔ yC = 1, portanto, C(0; 1)

III) Para os pontos A(3; 4), B(1; 0) e C(0; 1), tem-se:

D = = 1 – 3 – 4 = – 6

IV) A área do triângulo ABC é dada por

S = = = = 3

Resposta: B

8) Representando o quadrilátero no sistema cartesiano, tem-se:

A área do quadrilátero é dada por

= = 2

Resposta: 2u.a.

9) Representando o quadrilátero no sistema cartesiano, tem-se:

I) A área do triângulo ABC é S1 = = = 20,5

II) A área do triângulo ACD é S2 = = = 22

III) A área do quadrilátero ABCD é S1 + S2 = 20,5 + 22 = 42,5

Resposta: 42,5u.a.

10) Para os pontos A(1; 3), B(4; 7) e C(6; 5), tem-se:

I) AB = � (4 – 1)2 + (7 – 3)2 = � 9 + 16 = �25 = 5

II) AC = � (6 – 1)2 + (5 – 3)2 = � 25 + 4 = �29

III) BC = � (6 – 4)2 + (5 – 7)2 = � 4 + 4 = �8 = 2�2

IV)O perímetro do triângulo ABC é 5 + �29 + 2�2

V) A área do triângulo ABC é = = 7

Resposta:

11) Se os pontos A(7; 5), B(3; – 4) e C(x; 6), com x inteiro, formamum triângulo de área 29, então:

= 29 = 8⇔ – 28 + 5x + 18 + 4x – 42 – 15 = 58⇔

⇔ 9x – 67 = 58 ⇔ 9x – 67 = 58 ou 9x – 67 = – 58 ⇔

⇔ x = ou x = 1 ⇒ x = 1, pois x é inteiro

Resposta: x = 1

12) Se os pontos A ; 1 , B(– 3; 4) e C t; – são colineares,então:

= 0 ⇔ 2 + t + – 4t + + 3 = 0 ⇔

⇔ 8 + 4t + 6 – 16t + 1 + 12 = 0 ⇔ – 12t = – 27 ⇔ t = =

Resposta: A

13) Para os pontos A(1; 2), B(3; 4) e C(4; 5), tem-se:

D = = 0, portanto, A, B e C estão alinhados e

pertencem ao gráfico da função f(x) = x + 1, pois f(1) = 2, f(3) =4 e f(4) = 5

Resposta: D

14) A distância real entre o ponto de partida C da joaninha e o dechegada A é o comprimento da hipotenusa de um triânguloretângulo de catetos 2 m e 6 m.

Assim sendo, essa distância d, em metros, é:

d = �22+ 62 = �40 = 2�10

Resposta: A

310

401

111

6––2

| – 6 |––––––

2| D |––––

2

(3 + 1) . 1–––––––––

2(AC + BD) . h––––––––––––

2

41–––22

273

51

– 4

111

44–––22

23

– 2

5– 4– 3

111

14–––22

146

375

111

perímetro = 5 + 2�2 + �29� área = 7

2

73x

5– 46

111

125–––––

9

�1––2��1

––2�

1––4

3––2

1––2

– 3

t

1

4

1– ––2

1

1

1

9––4

27–––12

134

245

111

16 –

15)

Sendo x a medida do lado da malha quadriculada da figura 2,a medida do lado da malha quadriculada da figura 3 é 2x.

Assim, A’B’ = 4x, AB = 3x e, portanto, o fator de am pliação dafigura 2 para a figura 3 é:

= =

Resposta: C

Resposta: 12 u. a.

17) Se A, B e C são vértices de um triângulo, então neces saria -mente:

≠ 0 ⇔ – 6k + 6 + 6 – 3k ≠ 0 ⇔ 9k ≠ 12 ⇔ k ≠

Resposta: C

18) Sendo S a área do triângulo de vértices A(6;8), B(2;2) e C(8;4),temos:

S = = 14

Resposta: C

19) Os pontos A, B e C pertencem a uma mesma reta €

€ = 0 € x = – 4

Resposta: D

20) Os pontos A, B e P estão alinhados, então:

= 0 € k = – 5

Portanto: 3 . k + 2 = – 13

Resposta: C

n Módulo 18 –Equação Geral da Reta

1) I) O ponto A(a; 1) pertence à reta x + 2y = 0, então:

a + 2 . 1 = 0 ⇔ a = – 2 fi A(– 2; 1)

II) O ponto B(2; b) pertence à reta x + 2y = 0, então:

2 + 2b = 0 ⇔ b = – 1 fi B(2; – 1)

III) A distância entre os pontos A(–2; 1) e B(2; – 1) é

d = � (2 + 2)2 + (1 + 1)2 = � 16 + 4 = �20 = 2�5Resposta: A

2) I) O ponto (1; 2) pertence à reta y = 2x + p – 2q, então:2 = 2 . 1 + p – 2q ⇔ p – 2q = 0

II) O ponto (1; 2) pertence à reta y = x + q – 3, então:

2 = . 1 + q – 3 ⇔ q =

III) ⇔ ⇔ p + q = 7 + =

Resposta: C

3) I) O ponto P de intersecção das retas y = 2x + 1 e 5y + 2x – 2 = 0 é dado pela solução do sistema formadopelas duas equações, assim:

⇔ ⇔

⇔ fi P – ;

II) A reta vertical que passa pelo ponto P – ; tem

equação x = –

Resposta: C

4) A reta y = – 2 é horizontal, portanto, é mediatriz de umsegmento vertical, cujo ponto médio deve ter y = – 2. Umpossível segmento tem extremos A(0; 0) e B(0; – 4), pois

xA = xB e = = – 2

Resposta: A

5) A reta passa pelos pontos (0; 3) e (5; 0), assim, sua equação édada por:

= 0 ⇔ 3x + 5y – 15 = 0 ⇔

⇔ 5y = – 3x + 15 ⇔ y = – x + 3

Resposta: A

4–––3

4x––––3x

A’B’–––––AB

�– 24 �= –––––– = 12 u.a.

2

3 1 1�� – 3 1 1 ��5 5 1–––––––––––––

216) A�ABC =

4––3

111

0– 6

3

k21

6 8 1��2 2 1��8 4 1

––––––––––––––2

31x

5–1–16

111

111

31

k + 12

14k

3––2

7––2

3––2

21–––2

7––2

p = 77

q = ––2

�p – 2q = 0

7q = ––

2�

– 2x + y = 12x + 5y = 2�y = 2x + 1

5y + 2x – 2 = 0�

�1––2

1––4�

1x = – ––

41

y = ––2

��1

––2

1––4�

1––4

0 + (– 4)–––––––––

2

yA + yB–––––––––

2

05x

30y

111

3–––5

– 17

6) Os pontos I1 e I2 pertencem à parábola y = x2 e à reta

y = – x + 3, logo, suas coordenadas são as soluções do

sistema formado pelas duas equações, assim:

⇔ ⇔

A soma dos valores de x que satisfazem a equação

5x2 + 3x – 15 = 0 é = , que corresponde à soma das

abscissas dos pontos I1 e I2.

Resposta: A

7) A reta passa pelos pontos (– 2; 0) e (2; 3), assim, sua equaçãoé dada por:

= 0 ⇔ – 6 + 2y – 3x + 2y = 0 ⇔

⇔ – 3x + 4y – 6 = 0 ⇔ 3x – 4y + 6 = 0Resposta: C

8) I) Os pontos P(3; yP), (0; 8) e (4; 0) estão alinhados, pois per -tencem ao gráfico da função do 1o. grau f(x), então:

= 0 ⇔ 24 + 4yP – 32 = 0 ⇔ yP = 2 fi P(3; 2)

II) O gráfico da y = g(x) é uma reta que passa pelos pontos P(3; 2) e (– 1; 0), assim, sua equação é dada por:

= 0 ⇔ 2x – y + 2 – 3y = 0 ⇔ 2x – 4y + 2 = 0 ⇔

⇔ x – 2y + 1 = 0 ⇔ 2y = x + 1 ⇔ y =

Resposta: D

9) A reta passa pelos pontos (0; 3) e (4; 0), assim, sua equação édada por:

= 0 ⇔ 3x + 4y – 12 = 0

Outra maneira: A equação da reta cujas intersecções com os

eixos são (p; 0) e (0; q) é dada por + = 1, assim, para

os pontos (4; 0) e (0; 3), tem-se:

+ = 1 ⇔ 3x + 4y = 12 ⇔ 3x + 4y – 12 = 0

Resposta: D

10) I) Sendo P o ponto médio do lado —NQ, com N(2; 9) e Q(4; 3),

tem-se:

fi P(3; 6)

II) A mediana traçada do vértice M é o segmento de reta queune o vértice M(0; 0) e o ponto médio do lado

—NQ, dado

por P(3; 6), assim, sua equação é:

= 0 ⇔ 3y – 6x = 0 ⇔ 3y = 6x ⇔ y = 2x

Resposta: E

11) A equação da reta r que passa por (2; 5) e (5; 9) é dada por:

= 0 ⇔ 18 + 5x + 5y – 9x – 2y – 25 = 0 ⇔

⇔ – 4x + 3y – 7 = 0Um outro ponto dessa reta é (500; 669), pois, para x = 500tem-se: – 4 . 500 + 3y – 7 = 0 ⇔ 3y = 2007 ⇔ y = 669

Resposta: A

12) A equação da reta que passa por A(1; 2) e B(3; 3) é dada por:

= 0 ⇔ 3 + 2x + 3y – 3x – y – 6 = 0 ⇔

⇔ – x + 2y – 3 = 0 ⇔ 2y = x + 3 ⇔ y = +

Resposta: D

13) a) A reta x = – 3 é vertical e a distância ao ponto P(2; 10) é d = 2 – (– 3) = 2 + 3 = 5

b) A reta y = 6 é horizontal e a distância ao ponto P(2; 10) éd = 10 – 6 = 4

Respostas: a) 5 b) 4

14) a) Para que as retas ax – 5y + 7 = 0, 2x + ay – 8 = 0 e 2ax – 7y + 8 = 0 sejam concorrentes no mesmo ponto, osistema formado pelas três equações deve ter uma únicasolução (x; y), que cor responde ao ponto onde as retas seinterceptam, assim:

⇔ ⇔

⇔ ⇔ ⇔ ⇔

⇔ ⇔ ⇔ ⇔

⇔ ⇒ a = 1 ou a = 3

b) O ponto de intersecção é dado por

, assim:

I) Para a = 1 fi , então, o ponto é (3; 2).

II) Para a = 3 fi , então, o ponto é (1; 2).

Resposta: a) 1 ou 3 b) para a = 1 (3; 2)

para a = 3 (1; 2)

3–––5

y = x2

5x2 + 3x – 15 = 0�y = x2

3x2 = – ––x + 3

5�

y = x2

3y = – ––x + 3

5�

– 3––––

5– b––––

a

– 22x

03y

111

304

yP80

111

3– 1x

20y

111

x + 1––––––

2

04x

30y

111

y–––q

x–––p

y–––3

x–––4

xN + xQ 2 + 4xP = –––––––– = –––––– = 3

2 2yN + yQ 9 + 3

yP = –––––––– = –––––– = 62 2

�

03x

06y

111

25x

59y

111

13x

23y

111

3–––2

x–––2

ax – 5y = – 72x + ay = 82ax – 7y = – 8

� – 2

+

ax – 5y + 7 = 02x + ay – 8 = 02ax – 7y + 8 = 0

�ax – 10 = – 72x + 2a = 8y = 2

�ax – 5y = – 72x + ay = 8y = 2

�ax – 5y = – 72x + ay = 83y = 6

�3

4 – a = ––a

x = 4 – ay = 2

�3

x = ––a

x = 4 – ay = 2

�ax = 3x + a = 4y = 2

�a2 – 4a + 3 = 0x = 4 – ay = 2

�x = 4 – ay = 2�

x = 3y = 2�x = 1y = 2�

18 –

15) I) = 0 ⇔ – 2x + y + 3m + 2 – 3y – mx = 0 ⇔

⇔ (– 2 – m)x – 2y + 3m + 2 = 0

II) A reta x = 5 é vertical, assim, a reta obtida no item (I) deveser horizontal, isto é, a equação deve ser do tipo y = contante, independente do valor de x, portanto, deve-se ter: – 2 – m = 0 ⇔ m = – 2

Resposta: C

16) Uma reta paralela ao eixo y é uma reta vertical e sua equaçãoé do tipo x = constante, assim, para que a reta passe peloponto P(2; 3), a equação é dada por x = 2.Resposta: A

17) Os pontos A(3; – 2), B(m; n) e O(0; 0) estão alinhados, então:

= 0 ⇔ 2m + 3n = 0

Resposta: 2m + 3n = 0

18) I) O ponto P de intersecção das retas 3x + 5y – 7 = 0 e 4x + 6y – 5 = 0 é dado pela solução do sistema formadopelas duas equações, assim:

⇔ ⇔

⇔ ⇔ fi

⇔ fi P – ;

II) A reta paralela ao eixo Ox (horizontal) que passa pelo

ponto P – ; tem equação y = .

Resposta: C

19) I) A equação da reta que passa por (0; 5) e (3; 0) é dada por:

= 0 ⇔ 5x + 3y – 15 = 0

II) A equação da reta que passa por (0; 2) e (4; 0) é dada por:

= 0 ⇔ 2x + 4y – 8 = 0 ⇔ x + 2y – 4 = 0

III) O ponto P de intersecção das retas 5x + 3y – 15 = 0 e

x + 2y – 4 = 0 é dado pela solução do sistema formado

pelas duas equações, assim:

⇔ ⇔

⇔ ⇔ ⇔

⇔ ⇔ fi P ;

IV) A equação da reta r que passa por P ; e O(0; 0)

é dada por:

= 0 ⇔ x – y = 0 ⇔

⇔ 5x – 18y = 0 ⇔ 18y = 5x ⇔ y = x

Resposta: B

x31

y– 2m

111

3m0

– 2n0

111

3x + 5y = 74x + 6y = 5�3x + 5y – 7 = 0

4x + 6y – 5 = 0�2x = – 174x + 6y = 5�– 18x – 30y = – 42

20x + 30y = 25�

�13–––2

17–––2�

17x = – –––

213

y = –––2

�13–––2�13

–––2

17–––2�

03x

50y

111

04x

20y

111

5x + 3y = 15x = 4 – 2y�5x + 3y – 15 = 0

x + 2y – 4 = 0�

20 – 10y + 3y = 15x = 4 – 2y�5(4 – 2y) + 3y = 15

x = 4 – 2y�

�5–––7

18–––7�

5y = –––

718

x = –––7

�– 7y = – 5x = 4 – 2y�

�5–––7

18–––7�

18–––7

5–––7

18–––70x

5––70y

1

11

5–––18

– 19