Weak Gravitational Lensing

Tessa Baker

March 2, 2017

0 References

• Modern Cosmology, Scott Dodelson. Primary source for this lecture, and a really good all-roundtextbook for beginning grad student-level cosmology.

• Weak Gravitational Lensing of the CMB, Anthony Lewis & Anthony Challinor, arXiv: astro-ph/0601594.Comprehensive and pedagogical review paper covering both theory and applications of CMB lensing.§3.1 contains all that is needed for this lecture.

• Gravitation, Foundations and Frontiers, Thanu Padmanabhan. An excellent, if sometimes idiosyncratic,GR textbook – one of my favourites. Though it doesn’t contain much on gravitational lensing, I referenceit here for a proof of the conservation of surface brightness (see §3.2).

More heavy-duty:

• Gravitational Lensing: Strong, Weak and Micro, P. Schneider, C. Kochanek & J. Wambsganss. Lecturenotes from the Saas-Fee summer school. All four parts are available online; section 3 (weak lensing) isat https://arxiv.org/abs/astro-ph/0509252.

• Gravitational Lenses, P. Schneider, J. Ehlers & E. Falco. A classic, and with good reason. Rigorousand full of gems; far more detail than is needed for this course.

1 Introduction

Review of some basic facts we already know:

• massless particles like photons move along the null geodesics of a spacetime;

• the presence of mass induces spacetime curvature, i.e. the metric gµν is no longer the (flat) Minkowskimetric of Special Relativity;

• the null geodesics of a curved spacetime are not necessarily straight lines. The geodesic equationconfirms this qualitative notion:

d2xα

dλ2+ Γαµν

dxµ

dλ

dxν

dλ= 0 (1)

If Γαµν 6= 0 then this is no longer the equation of a straight line.

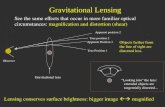
Taken together, these statements imply that light rays will be deflected – bent off their original path – bymassive objects. Note that when we look at the sky with our eyes or a telescope, we infer the position ofobjects by tracing back photons from them in a straight line. This means where we perceive an object to be(‘image position’) may be different to its true location (‘source position’), see Fig. 1. In some cases a bundleof light rays emitted from a source can be deflected onto multiple different paths. This results in us seeingmultiple images of the same source in different locations, see Fig. 2.

1

Figure 1: Deflection of light in a curved spacetime. In this case, the light of a distant star is deflected by thegravitational field of the Sun. Note that the location of the image corresponds to tracing the received rayback in a straight line.

Figure 2: The Einstein Cross is a multiply imaged quasar, lensed by an intervening galaxy that sits almostexactly in front of it. The quasar is located about 8 billion light years away, whilst the lensing galaxyis at 400 million light years. The angular size of the cross in the sky is roughly1.6 x 1.6 arcseconds; theright-hand panel shows a zoom-in. This is an example of strong gravitational lensing. Image credits:NASA/ESA/Hubble/STSci.

Two kinds of gravitational lensing appear in a cosmological context1: strong and weak. In strong lensingwe consider virtually all the deflection to be caused by a single massive object along the line of sight to thesource – there is one, extreme lensing event. For example, we observe that images of very distant galaxiescan be lensed (and hence distorted) by other (clusters of) galaxies closer to us, as shown in Fig. 2.

In contrast, weak lensing involves multiple, less extreme lensing events. These multiple lensing eventsoccur as a photon from a distant galaxy2 propagates towards us through the large-scale ‘cosmic web’ of darkmatter that fills the universe, see Fig. 3. These dark matter structures bend the path of the photon gently,with the result that our galaxy image gets lightly squished – see Fig. 4.

1There are also non-cosmological examples of gravitational lensing: lensing by the Sun during the solar eclipse of 1919 wasfamously the first attempted experimental test of General Relativity. Also, there are all sorts of interesting optical distortioneffects that can happen close to black hole event horizons, as a result of lensing by very strong gravitational fields.

2At the end of these notes we’ll consider a case where the source is not a galaxy, but the CMB itself.

2

Figure 3: Snapshot from the Millennium Simulation, showing the large-scale cosmic web. The purple filamentsindicate dark matter; the baryons/galaxies we observe are coloured gold/yellow. Image credit: the VirgoCollaboration.

Figure 4: Schematic indicating the subtle changes to a galaxy image induced by weak gravitational lensing.The image on the RHS has an increased ellipticity along the axis running 4 o’clock to 10 o’clock. Rememberthat the left panel is unobservable – we would only see the image on the right. Image credit: Sarah Bridle,Uni. Manchester.

As we’ll see shortly, we can use the effects of weak lensing – when measured for tens of thousands ofgalaxies – to learn about the contents of the universe, the statistics of the cosmic web structure, and to testGeneral Relativity and ideas about dark energy.

Although strong lensing does have the potential to measure the Hubble constant H0 (ask me at the endof the lecture if interested), at the moment it’s not as powerful a tool for cosmology as weak lensing. This isbecause to fully understand strong lensing measurements you need a detailed mass model of the low-redshiftcluster that is acting as the lens. This is difficult to obtain. Even if a good mass model can be constructed fora particular system, the process needs to be repeated for thousands of systems in order to make statisticallysignificant measurements of cosmological parameters.

The strategy employed in weak lensing is very different. Instead of requiring detailed knowledge aboutthe mass and structure of the lens, one looks for correlations between lensed galaxies in the same patch ofsky (where ‘correlations’ means that they have a tendency to be elongated in the same direction). There areboth current and upcoming experiments optimised to measure these correlations over large patches of skyquickly, e.g. the Dark Energy Survey (DES), the Large Synoptic Survey Telescope (LSST), the ESA Euclidsatellite.

3

Figure 5: Schematic showing the set-up for our calculation, and the locations χ~θ and χ~θS . Credit: S.Dodelson.

We will build up a description of weak lensing in the following stages:

1. We’ll start by using the GR and cosmology you already know to study the propagation of photons ina perturbed cosmological spacetime.

2. We’ll show how the paths of these geodesics can be used to construct a rank-2 tensor called the distortiontensor. We’ll also show how the distortion tensor describes the ellipticity of a galaxy, i.e. its deviationfrom a sphere (or really, a circle once projected on the sky).

3. We then set about building a power spectrum of this distortion tensor that encodes the correlationsbetween galaxy images as described above. In fact, there will be several different power spectra we cantalk about – because the distortion tensor is a rank-2 object, we can choose to correlate its componentsin various ways. We’ll tie up the results of this calculation to some real-world data from recent galaxysurveys.

4. If time permits, we’ll also discuss the related topic of CMB lensing.

2 Deflected Photon Geodesics

Fig. 5 shows the set-up we need. A photon is emitted from a point of the source (remember, it’s an extendedobject like a galaxy) and deflected by the gravitational field of another object in the lens plane3 To startwith, this looks a lot like a strong lensing scenario. This is just an artefact of drawing a convenient diagram– in reality there is a whole sequence of lensing masses along the line of sight between the observer and thesource.

We set up a system of coordinates as follows. There is a radial coordinate, χ, that describes radialcomoving distances from the observer according to:

χ(a or t) =

∫ t0

t

dt

a(t)=

∫ 1

a

1

a2H(a)da (2)

where I’ve indicated that the scale factor a can be used as an alternative to physical time.We’ll use two further coordinates in the plane perpendicular to the line of sight: since we expect galaxies

to be spherical on average, we can use polar coordinates. Making use of the small-angle approximation, wecan then denote a general point by the vector χ~θ = χ(θ1, θ2, 1). We want to find the mapping between apoint in the source, χ~θS and it’s location in the image plane.

3Since the size of the object doing the lensing is much smaller than the total distance travelled by the photon, we can ignoreit’s extent along the line of sight. This is called the thin-lens approximation.

4

Recall the following definition of the four-momentum of a photon, and the magnitude of its spatialcomponent p:

Pµ =dxµ

dλp2 = gijP

iP j (3)

where λ is an affine parameter. Of course, since a photon is null we must have PµPµ = 0; using the lineelement for a perturbed FRW spacetime:

ds2 = −(1 + 2Ψ)dt2 + a(t)2(1− 2Φ)δijdxidxj (4)

we can expand PµPµ = 0 to find:

−(1 + 2Ψ)(P 0)2 + p2 = 0 ⇒ P 0 = p(1 + 2Ψ)−12 ≈ p(1−Ψ) (5)

We’ll need this relation in a moment. We’ll also need the perturbed Christoffel symbols, which you knowhow to calculate from your GR course. You should be able to show that for the above line element these are:

Γ000 = Ψ Γi00 = ∂iΨ (6)

Γij0 = δij

(H − Φ

)Γijk = δimδij∂mΦ− δik∂jΦ− δij∂kΦ (7)

Note that since Φ and Ψ are small quantities, we’ve dropped all terms of order Φ2, Ψ2 and higher whenworking these out. Now let’s tackle the spatial component of the geodesic equation, eq.(1). We’ll bravelydevelop both LHS and RHS in parallel; our first step is to convert all derivatives to be w.r.t. χ by using thechain rule:

d2xi

dλ2= −Γiµν

dxµ

dλ

dxν

dλ

dt

dλ

dχ

dt

d

dχ

(d(χθi)

dχ

dχ

dt

dt

dλ

)= −Γiµν

dxµ

dχ

dxν

dχ

(dt

dλ

)2(dχdt

)2

d

dχ

(d(χθi)

dχ

dχ

dt

dt

dλ

)= −

[Γi00

(dx0

dχ

)2

+ Γi0jdx0

dχ

dxj

dχ+ Γijk

dxj

dχ

dxk

dχ

](dt

dλ

)(dχ

dt

)d

dχ

(−pa

d(χθi)

dχ

)≈ p

a

[a2∂iΨ− 2H

d(χθi)

dχ+ δim∂mΦ

](8)

where in the second line we’ve written ~x = χ~θ. In the third line we’ve expanded out the index summationand cancelled some factors. In the fourth line we’ve recognised that dt/dλ = P 0, and used eqs. 2, 5 & 7.We’ve also used the fact that θi is a small quantity, so terms like θi ×Φ can be neglected to first order. Thisis the reasoning behind the last term on the RHS; the only non-negligible contribution is when j = k = 3,i.e. the coordinate along the line of sight.

You know already (Baumann notes eq.1.2.50) that to first order the spatial 3-momentum redshifts asp ∝ 1/a. Using this in eq.8 (we don’t need to specify the constant of proportionality since it cancels fromboth sides):

d

dχ

(1

a2

d(χθi)

dχ

)≈[−∂i(Ψ + Φ) + 2

H

a

d(χθi)

dχ

](9)

1

a2

d2(χθi)

dχ2− 2

a3

da

dt

(dt

dχ

)d(χθi)

dχ≈[−∂i(Ψ + Φ) + 2

H

a

d(χθi)

dχ

](10)

d2(χθi)

dχ2≈ −a2∂i(Ψ + Φ) = −2δij∂jΦ (11)

where the second equality in the line directly above uses that at late times in the universe (so neutrinos andradiation are negligible) Φ = Ψ to a very good approximation4.

4This comes is comes from the Einstein equations, when evaluated to first order in linear perturbations. The equality of Φand Ψ is a feature (almost) unique to General Relativity. In lots of theories of modified gravity – put forwards as alternatives tothe cosmological constant explanation of accelerated expansion – we have Φ 6= Ψ. By combining observations in the right waywe can test for the equality of the metric potentials, and hence test ideas about dark energy.

5

Integrating once, twice (and going to pains to make the arguments of the metric potentials clear):

d(χθi)

dχ= −δij

∫ χ

0dχ ∂j [Ψ(~x(χ) + Φ(~x(χ)] + constant (12)

θiS = −δij

χ

∫ χ

0dχ′∫ χ′

0dχ ∂j [Ψ(~x(χ) + Φ(~x(χ)] + constant (13)

The LHS has picked up a subscript S in the last line because θi(χ) = θiS , the original location of the pointin the source plane. We now realise that the constant must be equal to θi, the point that θiS gets mapped toin the image: because if there is no lens present, the integral vanishes and we must be left with the trivialrelation θiS = θi.

Reversing the order of integration in eq.(13):

θiS = θi − δij

χ

∫ χ

0dχ

∫ χ

χdχ′ ∂j [Ψ(~x(χ) + Φ(~x(χ)] (14)

The innermost integral is now trivial, since the integrand only depends on χ.

θiS = θi − δij∫ χ

0dχ

{∂j [Ψ + Φ]

(1− χ

χ

)}(15)

where I’ve suppressed the arguments of the potentials again, for clarity. This is the key expression we’reseeking. It tells us that the difference between the the the original position of a point in our source and it’sobserved position in the image plane is controlled by the gradient of the gravitational potential due to thelens, modulo a weighting factor (the piece in round brackets) that encodes information about the relativeconformal distances to the lens and the source.

The additional complication is that, in the weak lensing case, this fairly intuitive5 quantity is integratedover a whole distribution of roughly equal-size lensing masses along the line of sight. In the strong lensingcase we would expect this integral to be dominated by the contribution at the distance of the main, extremelensing event.

3 The Distortion Tensor

3.1 Definition

Eq.15 only describes one component of our position vector χ~θ at a time. What we really want is an objectthat gives us the mapping between both transverse components at once (the longitudinal component alongthe χ axis is less interesting, since we can’t observe it directly6).

A common notation is to define a 2x2 matrix A using the derivative of eq.15:

Aij =∂θiS∂θj

(16)

Note that the first term on the RHS of eq.15 will give an identity matrix contribution to A. Once again, thiscorresponds to the trivial limit where no lens is present and the true and apparent positions are identical. Sowe introduce a second quantity, the distortion tensor, that describes any non-trivial difference between (thetransverse components of) χ~θS and χ~θ:

ψij = Aij − I2 =

(−κ− γ1 −γ2

−γ2 −κ+ γ1

)(17)

= −δik∫ χ

0dχ

{∂j∂k[Ψ + Φ] χ

(1− χ

χ

)}(18)

where the expansion into elements on the first line serves to define the quantities κ and γi that we’ll explorein a moment. Beware a devious χ that has appeared in the integrand above. This is because, for the

5Admittedly, perhaps only intuitive in hindsight.6We can still measure it, if we’re prepared to whip out a spectrograph and measure the redshift of spectral features in our

source galaxy.

6

Figure 6: Image ellipticity parameters. Note that the values of εi assigned to each image depend on thechoice of axes orientation. Credit: S. Dodelson.

distortion tensor, we really wanted to differentiate under the integrand w.r.t. θ. However, the derivativealready appearing in eq.15 is w.r.t. xj , so we have used the chain rule again to match it:

∂θiS∂θj

=∂θiS∂xk

∂xk

∂θj=∂θiS∂xk

∂(χθk)

∂θj=∂θiS∂xk

χδkj =∂θiS∂xj

χ (19)

In eq.(17) we have introduced some new variables to describe parts of the distortion tensor. These are theconvergence, κ, and the two components of the shear, γ1 and γ2. Broadly speaking, κ describes themagnification of an image with respect to the original source, and the γi describes how the shape of imagehas been distorted with respect to the original source by lensing.

3.2 Ellipticities and Shear

To explain the shear parameters more quantitatively, we first need to think about how to quantify theellipticity of an image. Imagine we have a function Iobs(θ) that describes how the brightness of an imagevaries with position. Integrating this function over the image would just give us the total flux of the source.So to get some measure of the shape of the source, we instead think about taking moments of the brightnessdistribution.

For images like those shown in the top line of in Fig. 6, the dipole moments vanish because there are equalportions in all four quadrants. The same is true of the images in the bottom line. The first non-vanishingmoments are instead the quadrupoles:

qij =

∫dθ Iobs(θ) θiθj (20)

These don’t vanish because the factor θiθj has the same sign in opposite quadrants, so they no longer canceleach other. By rotational symmetry, a perfectly circular image has qxx = qyy and qxy = 0. So, we can assessthe non-circularity of an image via the following quantities:

ε1 =qxx − qyyqxx + qyy

ε2 =2qxy

qxx + qyy(21)

Fig. 6 indicates how the signs of ε1 and ε2 describe the orientation of an elliptical image. Plugging eq.(20)into the first of eq.(21):

ε1 =

∫d2θIobs(θ) [θxθx − θyθy]∫d2θIobs(θ) [θxθx + θyθy]

(22)

7

Now, we use the fact that surface brightness is conserved between the source and the image7, such thatIobs(θ) = Itrue(θ

S). Using eq.(16), we can write that for small deflections the position of points in the source

and image planes are related by θi =(A−1

)jiθSj . Hence:

ε1 =

∫d2θS | detA−1|

[(A−1

)ix

(A−1

)jx−(A−1

)iy

(A−1

)jy

]Itrue(θ

S) θSi θSj∫

d2θS | detA−1|[(A−1)ix (A−1)jx + (A−1)iy (A−1)jy

]Itrue(θS) θSi θ

Sj

(23)

where detA−1 has appeared when we changed the integration variable to θS . Note that the A-matrices cannow be pullled outside of the integral, since they don’t depend on θS (indeed, the contents of the A matricesdescribe what happens to the photon *after* leaving the source plane).

We will take the average underlying, true source image of a galaxy to be circular. Of course this is nottrue for any given object, but when we average over thousands of randomly-oriented galaxies in a survey,it will be. Then the quadrupole moments of the true image vanish unless we have i = j; so the integralappearing in both the numerator and the denominator must be proportional to δij . Since the A matriceshave been taken outside, we now find we have exactly the same integrated quantity in both the numeratorand denominator. Cancelling them (and using the fact that A is symmetric), we arrive at:

ε1 =

[(A−1

)ix

(A−1

)jx−(A−1

)iy

(A−1

)jy

]δij[

(A−1)ix (A−1)jx + (A−1)iy (A−1)jy

]δij

(24)

=

[(A−1 x

x

)2 − (A−1 yy

)2]

[(A−1 x

x

)2+ 2

(A−1 x

y

)2+(A−1 x

x

)2] (25)

We can straightforwardly find the inverse matrix A−1 (but remember to add the identity matrix back ontoeq.(17)!)

A−1 =1

(1− κ)2 − γ21 − γ2

2

(1− κ+ γ1 γ2

γ2 1− κ− γ1

)(26)

Plugging the components of this into eq.(25):

ε1 =(1− κ+ γ1)2 − (1− κ− γ1)2

(1− κ+ γ1)2 + 2γ22 + (1− κ− γ1)2

(27)

=4γ1(1− κ)

2(1− κ)2 + 2γ21 + 2γ2

2

(28)

If the distortions and magnifications induced by lensing are small (which is the case for weak gravitationallensing), then we can drop quantities that are second-order in κ and γi. This leads to:

ε1 '4γ1

2(1− 2κ)' 2γ1 (29)

You can show, via a totally analogous calculation for ε2, that ε2 ' 2γ2. Hence measuring the shapes of manygalaxy images – and hence getting a statistical measurement of ε1 and ε2 in a particular direction on thesky – we can get estimates of γ1 and γ2. And these shear parameters, we know from eq.(17), are related to(derivatives) of the gravitational potential field.

7Gravitational lensing does not create or destroy photons – it merely alters their paths. True, a lens can deflect photons suchthat they reach an observer they otherwise would have missed. This means that the total integrated flux the observer receivesfrom that source is higher. However, the price paid for this is that the area of that source appears larger on the sky. Therefore thesurface brightness – the flux per unit source area (per unit time per frequency interval etc.) is conserved. See the Padmanabhanreference given at the start of these notes, p461, for a nice proof of this result using phase space densities.

8

3.3 Source Distribution

We nearly have all the pieces we need to start calculating observable quantities. However, so far we havediscussed only the distortion of light rays from a single source object (galaxy). As mentioned at the start,weak gravitational lensing involves correlating the distortions of a whole population of galaxies in order toprobe the large-scale gravitational field of cosmological structure. To do this, we need to integrate eq.(18)over a source population to find the total distortion tensor (which, with an abuse of notation, we will alsodenote as ψij).

We introduce a function W (χ) which describes the distribution of the redshifts of our source galaxies.The simplest example here would be a Gaussian peaked at (say) z ∼ 2. (Of course, this is not a realisticexample, as we’d expect our source distribution to die away more rapidly at high redshift where galaxiesbecome fainter and thus harder to detect.) We’ll take the function W (χ) to be appropriately normalised suchthat

∫W (χ) dχ = 1. Our total distortion tensor is then:

ψij = −δik∫ χ∞

0dχW (χ)

∫ χ

0dχ′

{∂j∂k[Ψ(~x) + Φ(~x)]χ′

(1− χ′

χ

)}(30)

where χ∞ is the furthest limit of our source population, and we’ve reminded ourselves that the gravitationalpotentials are functions of the position vector ~x = χ(θ1, θ2, 1). Reversing the order of integration like we didbefore, we can rewrite this as:

ψij = −δik∫ χ∞

0dχ ∂j∂k[Φ(~x)] g(χ) where g(χ) = 2χ

∫ χ∞

χ

(1− χ

χ′

)W (χ′) dχ′ (31)

To keep life simple, I’ve also adopted the GR case Ψ = Φ in the line above. We’ll stick with this limit fromnow on.

4 Power Spectra

We can finally bite the bullet and calculate power spectra of the components of the distortion tensor. Remem-ber, a power spectrum is just the Fourier-space version of a correlation function. And a correlation function– informally speaking – is simply something which tells you how closely related two points are8 as a functionof the distance between them. If you select any two points at random, there’s a chance that by fluke theymight have very similar field values. So instead, we have to average over many pairs of points. The generalkind of relation we will need multiple times in what follows is then (shown here for Φ):

〈Φ(~k)Φ∗(~k′)〉 = (2π)3 δ(3)(~k − ~k′)PΦ(k) (32)

Inverting this relation, one has:

PΦ(k) =

∫d3k′

(2π)3〈Φ(~k)Φ∗(~k′)〉 (33)

Note that: a) the definition of the power spectrum involves a complex conjugate. Because although Φ(~x)is real, its Fourier transform will pick up complex exponentials; and b) the power of 2π and kind of deltafunction on the RHS depend on the dimensionality of the Fourier-space variable. In the line above appearsa 3D wavevector ~k, which is conjugate to real-space 3D position vector ~x. In what follows, however, we willalso need the 2D Fourier variable ~, which is conjugate to our 2D angular position vector ~θ.

4.1 Power Spectrum of the Distortion Tensor

We’ll first form the power spectrum that correlates two general components of the distortion tensor (notethat this will be a four-index object). We’ll then see how to tease this apart into magnification and shearcomponents. Here goes:

Pψijpq(`) =

∫d2`′

(2π)2〈ψij(~)ψ∗pq(~′)〉 (34)

8More precisely, the field value at those two points.

9

where

ψij(~) =

∫d2θ ψij(~θ) e

−i~·~θ (35)

= −∫d2θ

∫ χ∞

0dχ ∂i∂j [Φ(~x)] g(χ) e−i

~·~θ (36)

=

∫d2θ

∫ χ∞

0dχ

∫d3k

(2π)3kikjΦ(~k) g(χ) e−i

~·~θei~k·~x (37)

where the first equality shows my conventions for a Fourier transform, the second equality uses eq.(31) andthe third line converts the real-space potential into its Fourier transform also. Note the derivatives havebecome factors of ki.

We squidge two copies of eq.(37) together (one C.C.) and use this in eq.(34). Note that this gives us ahorrendous seven-dimensional integral!

Pψijpq(~) =

∫d2`′

(2π)2

∫ χ∞

0dχ

∫ χ∞

0dχ′∫d2θ

∫d2θ′

∫d3k

(2π)3

∫d3k′

(2π)3

× kikjk′ik′j 〈Φ(~k)Φ∗(~k′)〉 g(χ)g(χ′) e−i(~·~θ−~′·~θ′)ei(

~k·~x−~k′·~x′) (38)

Don’t panic; we’re about to kill off a lot of these integrals. We start by replacing 〈ΦΦ∗〉 using eq.(32); thedelta-function then kills the k′ integral.

Pψijpq(~) =

∫d2`′

(2π)2

∫ χ∞

0dχ

∫ χ∞

0dχ′∫d2θ

∫d2θ′

∫d3k

(2π)3kikjkikj PΦ(k) g(χ)g(χ′) e−i(

~·~θ−~′·~θ′)ei~k·(~x−~x′)

(39)

Next up will be the θ and θ′ integrals. Note that the two exponentials, upon expansion of their arguments,are:

exp [−i (`1θ1 + `2θ2 − k1χθ1 − k2χθ2)] × exp[i(`′1θ

′1 + `′2θ

′2 − k1χ

′θ′1 − k2χ′θ′2)]× exp

[ik3

(χ− χ′

)]When we integrate over θ and θ′ the first two factors above will yield the delta functions δ(2)

(~− χ~k2D

)and

δ(2)(~′ − χ′~k2D

), alongside factors of 2π. ~k2D here explicitly refers to the first two components of ~k, which

reside in the image plane. The third component, corresponding to the direction along the line of sight, isseparated out in the last exponential above.

Pψijpq(~) =

∫d2`′

∫ χ∞

0dχ

∫ χ∞

0dχ′∫d3k

2πkikjkikj PΦ(k) g(χ)g(χ′)

× δ(2)(~− χ~k2D

)δ(2)

(~′ − χ′~k2D

)e[ik3(χ−χ′)] (40)

Now the k3 part of the d3k integral gives 2π δ(χ− χ′), which can be used to kill the χ′ integral.

Pψijpq(~) =

∫d2`′

∫ χ∞

0dχ

∫d2k2D kikjkikj PΦ(k) g(χ)2 δ(2)

(~− χ~k2D

)δ(2)

(~′ − χ~k2D

)(41)

Our LHS is just a function of `, but currently we have both ` and k on the RHS. So we’ll use one deltafunction to replace k by `′/χ, and rewrite the second delta function. Note that we can then remove the outerintegral in `′, since it’s now taken care of by the innermost one:

Pψijpq(~) =

∫ χ∞

0dχ

∫d2`′

χ2

`′i`′j`′p`′q

χ4PΦ(`/χ) g(χ)2 δ(2)

(~′ − ~

)(42)

Finally, the last delta function kills the `′ integral, leaving us with our result:

Pψijpq(~) =

∫ χ∞

0dχ

g(χ)2

χ2

`i`j`p`qχ4

PΦ(`/χ) (43)

10

4.2 Power Spectra for Shear and Convergence, E & B Modes

Pψijpq(~) above is the power spectrum showing the correlation between any two components ij and pq of the

distortion tensor; hence it’s a four-index object. We are particularly interested in the correlations for thecomponents of ψij that correspond to shear and convergence. Using eq.(17), we see that:

κ = −1

2(ψ11 + ψ22) (44)

γ1 =1

2(ψ22 − ψ11) (45)

γ2 = −ψ12 (46)

So we can see that the power spectrum of the convergence is:

Pκ(~) = 〈κκ∗〉 =1

4〈(ψ11 + ψ22) (ψ∗11 + ψ∗22)〉 (47)

=1

4[〈ψ11ψ

∗11)〉+ 〈ψ22ψ

∗22)〉+ 〈ψ11ψ

∗22)〉+ 〈ψ22ψ

∗11)〉] (48)

=1

4

[Pψ 1111(~) + Pψ 2222(~) + 2Pψ 1122(~)

](49)

Recall that ~ is a 2D vector, the Fourier conjugate to ~θ. We’re going to switch from describing it via twocomponents {`1, `2} to using a magnitude and an angle, i.e. `1 = ` cosφ and `2 = ` sinφ. This will enable usto make use of trig identities to simplify things.

Using this, together with eqs.(43) and (49), we get:

Pκ(`) =[sin4 φ+ cos4 φ+ 2 sin2 φ cos2 φ

] `44

∫ χ∞

0dχ

g(χ)2

χ6PΦ(`/χ) (50)

⇒ Pκ(`) =`4

4

∫ χ∞

0dχ

g(χ)2

χ6PΦ(`/χ) (51)

You can see that the leading bracket in the first line above is equal to unity. In a similar vein, the powerspectra of γ1 and γ2 are:

Pγ1(`, φ) = cos2(2φ)`4

4

∫ χ∞

0dχ

g(χ)2

χ6PΦ(`/χ) = cos2(2φ)Pκ(`) (52)

Pγ2(`, φ) = sin2(2φ)`4

4

∫ χ∞

0dχ

g(χ)2

χ6PΦ(`/χ) = sin2(2φ)Pκ(`) (53)

However, the two lines above say something slightly odd. They tell us that the power spectra for the shearcomponents depend on φ, which is the angle made with an arbitrarily chosen axis in the (Fourier-space)image plane. Clearly our choice of axis can’t have an effect on the underlying physics. This suggests that thePγi are not the most sensible variables to work with. It turns out that a particular linear combination of theshear components produces a power spectrum that is independent of φ.

Consider the following combinations:

E(`, φ) = cos(2φ)γ1(`, φ) + sin(2φ)γ2(`, φ) (54)

B(`, φ) = − sin(2φ)γ1(`, φ) + cos(2φ)γ2(`, φ) (55)

Now look what happens when we take the power spectrum of E (suppressing arguments for ease of notation):

PE(`) = cos2(2φ)Pγ1(`, φ) + sin2(2φ)Pγ2(`, φ) + 2 sin(2φ) cos(2φ)Pγ1 γ2(`, φ) (56)

We need

Pγ1 γ2(`, φ) = −1

2〈ψ12 (ψ22 − ψ11)〉 (57)

= −1

2[Pψ 1222 − Pψ 1211] (58)

= −`4

2

[sin3 φ cosφ− sinφ cos3 φ

] ∫ χ∞

0dχ

g(χ)2

χ6PΦ(`/χ) (59)

= 2 sinφ cosφ[cos2 φ− sin2 φ

]Pκ(`) (60)

= sin(2φ) cos(2φ)Pκ(`) (61)

11

Figure 7: E- and B-mode correlation functions from the KiloDegree Survey (KiDS), Kuijken et al. (2014).See text for description.

Stick this into eq.(56) and use eqs.(52) and (53):

PE(`) = cos2(2φ)Pγ1(`, φ) + sin2(2φ)Pγ2(`, φ) + 2 sin2(2φ) cos2(2φ)Pκ(`) (62)

⇒ PE(`) = Pκ(`) (63)

Whereas for the power spectrum of B we find:

PB(`) = sin2(2φ)Pγ1(`, φ) + cos2(2φ)Pγ2(`, φ)− 2 sin(2φ) cos(2φ)Pγ1 γ2(`, φ) (64)

=[sin2(2φ) cos2(2φ) + cos2(2φ) sin2(2φ)− 2 sin2(2φ) cos2(2φ)

]Pκ(`) (65)

⇒ PB(`) = 0 (66)

These results are massively useful. Firstly, eq.(63) tells us how to extract real, physical information that isindependent of any observer-imposed coordinate choice. What’s more, if we use our shear measurements tocalculate the power spectrum of the E-mode, we get the convergence (magnification) power spectrum for free.Eq.(66) is also extremely important because it allows us to check for systematics (i.e. unmodelled sourcesof error) in our measurements. If we’ve done our job properly9, then the B-mode power spectrum shouldvanish.

Fig. 4.2 shows measurements of the E and B-mode correlation functions from the KiloDegree Survey, thelargest dedicated weak lensing survey to date. Note that these plots show the real-space correlation function,which is the Fourier transform of the power spectra calculated above. Nevertheless, the basic information

9There are a lot of subtleties to be accounted for when measuring lensing shear, such as errors in our galaxy redshifts (anecessary evil of trying to survey large numbers of galaxies very quickly) and intrinsic alignments (the fact that galaxies neareach other are likely be aligned anyway due to local gravitational fields, and not just because intervening dark matter structureslens their photons in the same direction).

12

content is the same. Note also that in the B-mode plot, the correlation function has been multiplied by θ toemphasise deviations from zero at large angular separations.

The blue, dashed line shows a naive interpretation of the raw data. The pink (open) points show thedata after removing from the sample some patches of sky where the observations were particularly poor inquality (due to bad weather, obscuring dust in our own galaxy etc.) The black, solid line shows the data afterapplying further corrections for errors introduced by instrumental effects, i.e. miscalibrations or other errorsintroduced by the telescope itself. You can see that after sufficient error budgeting, the data are consistentwith a zero B-mode spectrum10. However, these curves also show just how crucial error management is forcorrect interpretation of weak lensing data!

5 Lensing of the Cosmic Microwave Background

In previous lectures you’ve studied how the cosmic microwave background (CMB) is produced during theearly thermal history of the universe. You’ve also seen that features in the CMB – anisotropies – can tell ussomething about inflation and cosmological parameters, and so are an intense object of study.

Problem: in this lecture we’ve calculated how images of distant galaxies get distorted as their photonspass through large-scale potential wells in the universe. Shouldn’t exactly the same thing be happening tothe CMB photons11? Doesn’t this mean, then, that the CMB anisotropies we’re so keen to study actuallyget ‘moved around’, changed by lensing en route to us?

This turns out to be exactly correct. Fortunately, as we will estimate below, the effect of lensing on theCMB is not so large as to eradicate all the useful information from it. However, it is large enough to have ameasurable effect that must be carefully modelled, and is of interest in its own right.

5.1 Order of Magnitude Estimates

Recall from your GR course that the angular deflection of a particle by a point mass is:

α =4GM

bc2∼ 2Φ

c2(67)

where b is the impact parameter between the particle and the point mass. You’ve learnt in this course thatthe large-scale potential wells in the universe have a depth of about ∼ 10−5. They also have an averagecomoving size of around 300 Mpc12. The CMB itself is at a comoving distance of ∼ 14 Gpc from us, so weexpect a CMB photon to have passed through roughly 14× 103/300 ∼ 50 such potential wells. Therefore wecould estimate its total deflection from its original direction of motion (at the time of last scattering) to beroughly 50× 10−5 ∼ 10−4 radians, which is of order an arcminute in degrees.

At the same time, the angular scale subtended by our ‘average’ potential well on the sky – taking it tobe roughly halfway between us and the CMB – is about 300/1400 ∼ 2◦. So, although our CMB photons areonly being diverted by an arcminute or so, we expect their deflections to be coherent over angular scales ofdegrees.

Recall that the first peak in the power spectrum of the CMB is at scales of around 1◦. Remember alsothat the power spectrum shows information effectively averaged over all directions in the sky. So althoughindividual anisotropies may get deflected in a particular direction, the net effect of lensing on the CMB powerspectrum is that it ‘blurs out’ the scale of the CMB peaks in general. The size of the first acoustic peakanisotropies gets increased by 2′/1◦ ∼ 3%. As one goes to smaller scales in the CMB, the relative effect ofthis blurring becomes larger.

10The error bars in Fig. 4.2 show the 1σ errors; remember you need a 3σ effect (at least!) to claim a statistically significantdeviation from zero.

11Of course the CMB photons, being in the microwave part of the EM spectrum, are of much lower frequency than opticalgalaxy images, but this makes no difference. Gravitational lensing is achromatic, i.e. it does not depend on photon frequency.

12This is rather sloppy. There are potential wells of all physical sizes in the universe, and defining an average is a bit meaningless.I really mean that the peak of the matter power spectrum is at scales corresponding to ∼ 300 Mpc.

13

5.2 Power Spectrum of the CMB Lensing Potential

Consider that CMB photons originally travelling in the direction ~n get deflected through an angle ~α suchthat their direction is ~n′ = ~n+ ~α. We write the CMB temperature measured in that new direction as:

T(~n′)

= T(~n+ ~α

)(68)

The expression for the deflection angle ~α is exactly what we worked out in eq.(15). The only change we needmake is changing the upper limit of the integral to a fixed distance χ∗, the conformal distance to the CMB.Unlike the galaxy weak lensing case, where we needed to integrate over a source distribution W (χ), for CMBlensing all our source photons come from the same redshift13.

To lowest order, we can write ~α as the gradient of a scalar potential β, i.e.

~α = ∇β =∇angβ

χ(69)

where ∇ang is the angular derivative on the sphere at conformal distance χ. Using our eq.(15), we can thenwrite:

β(~n) = −2

∫ χ∗

0dχ

(χ∗ − χχχ∗

)Φ[~x(χ, ~n)] (70)

where β is the CMB lensing potential and we have shown explicitly the direction of observation as anargument. The CMB lensing potential is often denoted by ψ; I’ve avoided this here to prevent confusion withthe distortion tensor of weak galaxy lensing. Once again we have specialised to the GR case of Φ = Ψ above.

We now want to find the power spectrum of β. The calculation is quite similar to that of §4, but somewhateasier because of the lack of indices on β. We start by Fourier transforming the potential as usual (this timesticking to k and x instead of ` and θ):

Φ(~x) =

∫d3k

(2π)3Φ(~k) ei

~k·~x (71)

Taking the two-point correlation function of β (and writing f(χ) = (χ∗ − χ)/χχ∗):

〈β(~n)β∗(~n′)〉 = 4

∫ χ∗

0dχ

∫ χ∗

0dχ′ f(χ) f(χ′)

∫d3k

(2π)3

∫d3k′

(2π)3〈Φ(~k)Φ(~k′)〉 ei(~k·~x−~k′·~x′) (72)

= 4

∫ χ∗

0dχ

∫ χ∗

0dχ′ f(χ) f(χ′)

∫d3k

(2π)3PΦ(~k, χ) ei

~k·(~x−·~x′) (73)

This time we’ll make use of the following identity for the expansion of Fourier basis functions:

ei~k·~x = 4π

∑`m

i` j`(kχ)Y ∗`m(~n)Y`m(~k) (74)

where j` are the spherical Bessel functions. Using this and breaking the d3k integral into angular and radialparts:

〈β(~n)β∗(~n′)〉 = 64π2

∫ χ∗

0dχ

∫ χ∗

0dχ′ f(χ) f(χ′)

∫ ∫ π

θ=0

∫ 2π

φ=0

k2 dk

(2π)3dθ dφ

× PΦ(~k, χ)∑

``′mm′

i`−`′j`(kχ) j`(kχ

′)Y ∗`m(~n)Y`m(~k)Y`′m′(~n

′)Y ∗`′m′(~k′) (75)

= 16

∫ χ∗

0dχ

∫ χ∗

0dχ′ f(χ) f(χ′)

∫k2 dk

2πPΦ(~k, χ)

∑``′mm′

j`(kχ) j`(kχ′)Y ∗`m(~n)Y`′m′(~n) δ``′δmm′ (76)

where we have used the orthogonality condition of the spherical harmonics to reach the second equality.

13We are approximating last scattering as being an instantaneous event. Of course this is not strictly true.

14

1 10 100 100010

−9

10−8

10−7

10−6

[l(l

+1)]2Cψ l/2π

l

Figure 8: Power spectrum of the CMB lensing potential, as per eq.(81). The dashed line shows a model thataccounts for corrections beyond linear perturbation theory; these become increasingly important at smallangular scales (high `).

Now we work on the LHS side a little. For CMB-related quantities, it’s usual to express power spectrain terms of the ‘C`’. These are the the two-point correlators of the Fourier coefficients when a quantity isexpanded in terms of spherical harmonics. That is,

β(~n) =∑`m

β`m Y`m(~n) (77)

⇒ 〈β`mβ∗`′m′〉 = δ` `′ δmm′Cβ` (78)

The superscript β on C` here is just to make it clear these are the C` describing the CMB lensing potential.You’ll also find in the literature/textbooks C` describing the CMB temperature power spectrum, E and Bpolarisation modes, etc. Using the two lines above in the LHS of eq.(76), we can read off (i.e. stripping offthe delta functions and Y`ms):

Cβ` = 16

∫ χ∗

0dχ

∫ χ∗

0dχ′ f(χ) f(χ′)

∫k2 dk

2πPΦ(~k, χ) j`(kχ) j`(kχ

′) (79)

One final simplification: in linear theory, we can relate the potential at a given instant of time to a primordialperturbation (at the same value of k) via a transfer function, i.e.

Φ(~k, χ) = TΦ(k, χ)R(~k) (80)

where we’re implicitly using conformal distance χ as a time variable here. R is a primordial perturbationlaid down during inflation, and TΦ describes how that initial perturbation has grown. In general TΦ is acomplicated function (and sometimes can’t be written down analytically), but it can be calculated numerically.Our final result can then be written as:

Cβ` =8

π

∫k2 dk PR(~k, χ)

[∫ χ∗

0dχ f(χ)TΦ(k, η) j`(kχ)

]2

(81)

where PR is the primordial power spectrum. It is described by a small number of cosmological parameters,which are relatively well-measured. Fig. 8 shows the results of this calculation for the power spectrum of theCMB lensing potential, and Fig. 9 shows the latest data from the Planck CMB satellite and the ground-basedACT and SPT telescopes. Note the x-axis is only a partial log in the second figure, hence the slightly differentshapes of Figs. 8 & 9.

15

−0.5

0

0.5

1

1.5

2

1 10 100 500 1000 2000

[L(L

+1)]2Cφφ

L/2π[×

107]

L

Planck (2015)

Planck (2013)

SPTACT

Figure 9: Measurements of the CMB lensing potential power spectrum from Planck, the South Pole Telescope(SPT) and the Atacama Cosmology Telescope (ACT). The solid line shows the prediction from the standardcosmological model, ΛCDM.

16