Trig Functions Review (Including Trig Quiz Solutions)
description
Transcript of Trig Functions Review (Including Trig Quiz Solutions)

Trig Functions Review(Including Trig Quiz Solutions)
MHF4UIFriday November 16th, 2012

Convert the following angles to Radians. Provide Exact Answers

Convert the following angles to Degrees. Round to the nearest degree.

Question 3: Finding the Arc Length
Therefore he travelled a distance of about 86.39 metres.
Therefore his angular velocity is per minute.

Question 6: Solve the Equation

Why must we have
In a right angled triangle, the absolute value of the length of the hyp will always be greater than or equal to absolute value of the length of the adj
Therefore

What is a Radian?
Much like a degree, a Radian is a measurement of an angle.
The radian measure of an angle ,ϴ, is defined as the length, a, of the arc that “subtends” the angle divided by the radius of the arc ,r
𝜃=𝑎𝑟

Radian Relationship to Degrees

Word Problems

Trig Ratios
Within a right angled triangle we will have that:

Finding Trig Ratios
We found Trig Ratios using our Related Acute angles of:
We found trig ratios by drawing our angles in standard position.
We found trig ratios when our terminal arm lies on the x or y axis.
We also used trig ratios to solve word problems (Kite Example)

Solving Trig Equations
We solved for simple trig equations by using our special acute angles.
We solved for trig equations by using our trig inverse function and finding
We also encountered cases where we had to rearrange our equation and isolate our trig function.
We used factoring or the quadratic formula to solve trig equations.
When we solved Trig Equations we must note the restriction on our solution:
- - No restrictions (infinite solutions)
- - other restrictions (we added or subtracted )

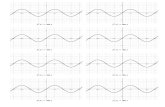
Graphing Trig Functions
We sketched the graphs of all 6 trig functions
We found the characteristics of each of these trig functions:- Max/Min- Amplitude- Period- Intercepts- Asymptotes

Transformations of Sinusoidal Functions
The general form of a Sinusoidal Function can be written as:
OR
We discussed the effects of variables a, k, c and d on the functionWe used mapping notation to graph our transformed functions
We found the 5 key points for both sine and cosine functions
We also used formulas of amplitude, period, vertical shift as well as our knowledge of the behaviour of sine and cosine functions to find the
equation in general form

Applications of Sinusoidal Functions
We applied sine and cosine functions to real life scenarios where we:
• Sketched the function• Found the characteristics of the function
• Found the equation of the function that would model the scenario• Solved for specific values of the function