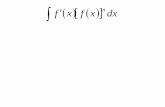The Derivative Function

Bacteria Growth

From looking at the the average rate of change of this function from data collected every two hours determine: • Where is the function increasing/decreasing? • Where is the function concave up/down?

Warming UPExercise 7 from Derivative at a Point

Consider the graph below. The domain of the function is all the real numbers. Assume that outside the window the function

continues the same behavior as the one indicated in the window.

1. Where is f(x) increasing?

2. Where is f(x)>0?

3. Where is f(x) concave up?

i. Draw the tangent line at each of the given points and use the grid to complete the table below. All the answers are estimates

ii. Use interval notation to complete the following informationa. Intervals where the derivative is negative

(solutions to f ‘ (x) < 0)

b. Intervals where f(x) < 0. Describe those points graphically.

c. Intervals where the derivative is positive (solutions to f ‘ (x) > 0)

d. Intervals where f (x) > 0. Describe those points graphically.

Critical Points of A Continuous Function

A critical points of a continuous function y=f(x) is a point in its domain where either f ‘(x)=0 or f ‘(x) is undefined. f’(x)=0 when the tangent line is horizontal f’(x) is undefined at a point in the domain where the tangent line does not exist (cusp, corner, end point), or when the tangent line is vertical..

If x0 is not a critical point its derivative exists and eitherf ‘(x0) > 0, or f ‘(x) < 0

Exercise 1

The first coordinate of the critical points of each of the functions below are identified at the top of each graph. Refer to the definition of a critical point to explain why it is a critical point. Identify the type of critical point (f ’=0 or f ’ undefined)

Exercisehttp://webspace.ship.edu/msrenault/GeoGebraCalculus/derivative_as_a_function.html

• Identify all the critical points on the given domain

• Determine the sign of the derivative between any two critical points

• Estimate the derivative (draw tangent lines to find them) at x=-2, 0, 2, 4, 6

• Click on the link above and produce the graph of its derivative.

• Compare your results with the applet

Derivative Function

Given a function y=f(x) a new function is defined the following way: to each point in the domain of the function y = f(x) the value of the derivative at that point is assigned, or what is the same the value of the slope of the tangent line. This new function is called the derivative function of y = f(x). The derivative function of y=f(x) is denoted

Derivatives of Basic Functions

1. Open the down menu (bottom) and choose one of the basic functions2. From the graph of the function identify

a. Critical points and classify themb. Intervals where the derivative is positivec. Intervals where the derivative is negative

3. Use the applet (check all the boxes) to generate the derivative function and verify your answers on part 2

4. Your next task is to produce the formula for the derivative function: a. Conjecture the type of graph the derivative would beb. By choosing points on the graph of the derivative function produce

its formula

More Functions To Find Their Derivative

Explore the derivative function for each of the following functions and produce their formulas

Deriving Basic Derivative Formulas

If f(x)=c, constant f ‘( c )=0

y=m x + b , y ‘=m

y(x)=x2, y ‘(x)=2x

Derivative of a Power Function

Exercise 5

Rewrite each of the following functions as a power function. Use the shortcut for the derivative of power functions to find the derivative. Give the final answer with positive exponents.

For each of the functions above find all their critical points

Basic Derivatives