In the previous lesson we introduced Exponential Functions and their

graphs, and covered an application of Exponential Functions (Compound

Interest). We saw that when interest is compounded 𝑛 times per year for

some number of years, the accumulated value of that investment can be

found by using the formula 𝐴 = 𝑃 (1 +𝑟

𝑛)

𝑛𝑡. Using that formula we can

find the accumulated value of investments when interest is compounded

bi-annually (𝑛 = 2), quarterly (𝑛 = 4), monthly (𝑛 = 12), weekly (𝑛 = 52), etc. But what would happen if the number of compounding

periods per year (𝑛) continued to increase? For instance what if interest

were compounded every day (𝑛 = 365), or every hour (𝑛 = 8760), or

every minute (𝑛 = 525,000), or every second (𝑛 = 31,536, 000)? For a

simple example, imagine that one dollar is invested for one year at a rate

of 100% (𝑃, 𝑡, and 𝑟 = 1); what would that investment accumulate to if

the number of compounding periods continued to increase?

How often is

interest

compounded?

𝒏 𝑨 = 𝑷 (𝟏 +𝒓

𝒏)

𝒏𝒕

monthly 12 𝐴 = 1 (1 +1

12)

12∙1

≈ 2.61303529 …

weekly 52 𝐴 = 1 (1 +1

52)

52∙1

≈ 2.69259695 …

daily 365 𝐴 = 1 (1 +1

365)

365∙1

≈ 2.71456748 …

every hour 8760 𝐴 ≈ 2.71812669161742 …

every minute 525,000 𝐴 ≈ 2.71827924258871 …

every second 31,536,000 𝐴 ≈ 2.71828178130146 …

continuously 𝑛 → ∞ 𝐴 ≈ 2.71828182845902 …

What we see is

that as the number

of compounding

periods per year

increase (𝑛 → ∞),

the accumulated

value 𝐴 continues

to get closer and

closer to the value

2.718281828 … .

This value that we

get closer and

closer to is known

as the natural

number 𝑒, and it is

used in finance (as

we’ll see later

with our second

compound interest

formula), as well

as in other

disciplines such as

statistics and

engineering.

The Natural Number 𝒆:

- a non-terminating constant 2.718281828 …

o to find the value on your calculator press the number 1, then the

2nd function button, then the LN button

- it is NOT a variable like 𝑥 or 𝑦, but rather a number like 𝜋

The way we will use the natural number 𝑒 is either as the base of an

exponential function, which is known as the natural exponential function

𝑓(𝑥) = 𝑒𝑥, or as the base of a logarithmic function, which is known as the

natural logarithmic function 𝑔(𝑥) = ln(𝑥). We will work with the

Natural Exponential Function 𝑓(𝑥) = 𝑒𝑥 in this lesson, and we’ll cover

the Natural Logarithmic Function 𝑔(𝑥) = ln(𝑥) in Lesson 32.

Natural Exponential Functions:

- 𝑓(𝑥) = 𝑒𝑥, where the exponent 𝑥 is a variable and base 𝑒 is the

natural number 2.71828 …

Just like any other exponential function, the domain of the natural

exponential function 𝑓(𝑥) = 𝑒𝑥 is unrestricted (−∞, ∞) and the range is

only positive numbers (0, ∞). And just like any other exponential

function, the natural exponential function 𝑓(𝑥) = 𝑒𝑥 can be transformed,

which in the case of a vertical transformation would alter the range.

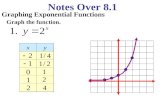
Example 1: Given the input/output table for the function 𝑓(𝑥) = 𝑒𝑥, as

well as its graph, find its domain, range, zeros, positive/negative intervals,

increasing/decreasing intervals, and intercepts.

Inputs Outputs

𝑥 𝑓(𝑥) = 𝑒𝑥

𝑥 → −∞ 𝑓(𝑥) → 0

−5 𝑓(−5) = 𝑒−5 =1

𝑒5≈ 0.01

−4 𝑓(−4) = 𝑒−4 =1

𝑒4≈ 0.02

−3 𝑓(−3) = 𝑒−3 =1

𝑒3≈ 0.05

−2 𝑓(−2) = 𝑒−2 =1

𝑒2≈ 0.14

−1 𝑓(−1) = 𝑒−1 =1

𝑒1≈ 0.37

0 𝑓(0) = 𝑒0 = 1

1 𝑓(1) = 𝑒1 ≈ 2.718281 …

2 𝑓(2) = 𝑒2 ≈ 7.389056 …

3 𝑓(3) = 𝑒3 ≈ 20.08553 …

4 𝑓(4) = 𝑒4 ≈ 54.59815 …

5 𝑓(5) = 𝑒5 ≈ 148.4131 …

𝑥 → ∞ 𝑓(𝑥) → ∞

Domain: (−∞, ∞)

Range: (𝟎, ∞)

Zeros: 𝐍𝐎𝐍𝐄

𝑓(𝑥) ≠ 0

Positive intervals: 𝑓(𝑥) > 0 when 𝑥 is (−∞, ∞)

Negative intervals: 𝑓(𝑥) < 0 when 𝑥 is 𝐍𝐎𝐍𝐄

𝐈𝐧𝐜𝐫𝐞𝐚𝐬𝐢𝐧𝐠 𝐢𝐧𝐭𝐞𝐫𝐯𝐚𝐥𝐬: 𝒇(𝒙) 𝐢𝐬 𝐫𝐢𝐬𝐢𝐧𝐠 𝐰𝐡𝐞𝐧 𝒙 𝐢𝐬 (−∞, ∞)

Decreasing intervals: 𝑓(𝑥) is falling when 𝑥 is 𝐍𝐎𝐍𝐄

Intercepts: 𝑥 − intercept: 𝐍𝐎𝐍𝐄 𝑦 − intercept: (𝟎, 𝟏)

𝑓(𝑥) = 𝑒𝑥

Notice that the graph of

𝑓(𝑥) = 𝑒𝑥 is increasing

throughout its domain.

When a function is

always increasing or

always decreasing that

function is one-to-one,

and it will have an

inverse function. All

exponential functions are

one-to-one, therefore all

exponential functions

have an inverse (we’ll

discuss this further in

Lessons 31 & 32).

𝑓(𝑥)

Outputs

Notice that just like the graph of 2𝑥, the graph of 𝑒𝑥 has a horizontal

asymptote at 𝑦 = 0 (the 𝑥-axis). That is because the graphs of both 2𝑥

and 𝑒𝑥 approach the 𝑥-axis, but they never touch it or cross it.

Example 2: Re-write the function 𝑔(𝑥) = 𝑒−𝑥 in terms of

𝑓(𝑥) = 𝑒𝑥. Then find the 𝑦-intercept of 𝑔 and find its graph by

transforming the graph of the original function 𝑓. Enter exact answers

only (no approximations) for the 𝑦-intercept.

𝑓(𝑥) = 𝑒𝑥 𝑓(𝑥)

Outputs

𝑥

Inputs

Inputs Outputs

𝑥 𝑓(𝑥) = 𝑒𝑥

𝑥 → −∞ 𝑓(𝑥) → 0

−2 1

𝑒2≈ 0.14

−1 1

𝑒≈ 0.37

0 1

1 𝑒 ≈ 2.72

2 𝑒2 ≈ 7.39

𝑥 → ∞ 𝑓(𝑥) → ∞

Re − write 𝑔(𝑥) in terms of 𝑓(𝑥):

𝒈(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝑔(0) =

(𝟎, )

Example 3: Re-write each of the following functions in terms of

𝑓(𝑥) = 𝑒𝑥, then transformation the graph of 𝑓. Also, find the 𝑦-intercept

for each function and enter exact answers only, no approximations.

a. ℎ(𝑥) = 𝑒𝑥 + 2

𝒉(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

b. 𝑗(𝑥) = −𝑒𝑥

𝒋(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

c. 𝑘(𝑥) = 2𝑒𝑥

𝒌(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝑓(𝑥) Outputs

𝑥 Inputs

𝑓(𝑥)

Outputs

𝑥 Inputs

𝑥 Inputs

𝑓(𝑥) Outputs

Example 4: Re-write each of the following functions in terms of

𝑓(𝑥) = 𝑒𝑥, then transformation the graph of 𝑓. Also, find the 𝑦-intercept

for each function and ENTER EXACT ANSWERS ONLY,

NO APPROXIMATIONS.

a. 𝑚(𝑥) = 𝑒𝑥−2

𝒎(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝒋(𝒙) =

b. 𝑛(𝑥) = −𝑒𝑥+1

𝒏(𝒙) =

𝒚 − 𝐢𝐧𝐭𝐞𝐫𝐜𝐞𝐩𝐭:

𝑓(𝑥) Outputs

𝑥 Inputs

𝑓(𝑥)

Outputs

𝑥 Inputs

Answers to Examples:

2. 𝑔(𝑥) = 𝑓(−𝑥), 𝑦 − intercept: (0,1) ;

3a. ℎ(𝑥) = 𝑓(𝑥) + 2, 𝑦 − intercept: (0, 3) ;

3b. 𝑗(𝑥) = −𝑓(𝑥), 𝑦 − intercept: (0, −1) ;

3c. 𝑘(𝑥) = 2𝑓(𝑥), 𝑦 − intercept: (0, 2) ;

4a. 𝑚(𝑥) = 𝑓(𝑥 − 2), 𝑦 − intercept: (0,1

𝑒2) ;

4b. 𝑛(𝑥) = −𝑓(𝑥 + 1), 𝑦 − intercept: (0, −𝑒) ;