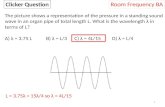
Clicker Question: Clicker Question: Clicker Question: Quantum ...
Multiplying Real Numbers Section 2.4 You need a Clicker If equations are trains threading the...
-
Upload
abner-owen -
Category
Documents
-
view
215 -
download
0
Transcript of Multiplying Real Numbers Section 2.4 You need a Clicker If equations are trains threading the...
Multiplying Real Multiplying Real NumbersNumbers
Section 2.4Section 2.4
You need a Clicker
If equations are trains threading the landscape of
numbers, then no train stops at pi. ~Richard Preston
The ConceptThe Concept► Today we’re going to build on our Today we’re going to build on our
understanding of arithmetic with positive understanding of arithmetic with positive and negative numbersand negative numbers
► We’ll look at multiplication through this We’ll look at multiplication through this lens and develop our rules of lens and develop our rules of multiplicationmultiplication
Multiplication DefinedMultiplication Defined
► Multiplication is simply repeated additionMultiplication is simply repeated addition► As such we can expand our understanding to As such we can expand our understanding to
include negative numbersinclude negative numbers► On a number line, we actually see the repetition of On a number line, we actually see the repetition of
a positive or negative number a certain number or a positive or negative number a certain number or positive timespositive times
► This gives us trouble when we multiply two This gives us trouble when we multiply two negatives, but this is handled via the multiplicative negatives, but this is handled via the multiplicative inverse propertyinverse property
The RulesThe Rules►The rules for positive and negative The rules for positive and negative
numbers with multiplication are very numbers with multiplication are very easyeasy Positive • Positive=PositivePositive • Positive=Positive Negative • Negative=PositiveNegative • Negative=Positive Positive • Negative=NegativePositive • Negative=Negative
ExampleExample
►Perform the arithmeticPerform the arithmetic
3( )( 4)
4n m
3.16
.
12.
4.3
A mn
B mn
C mn
D mn
The properties from The properties from yesterdayyesterday
Our properties of multiplication are not unlike our ones for addition:Our properties of multiplication are not unlike our ones for addition:► Commutative propertyCommutative property
a•b=b•aa•b=b•a Order doesn’t matter in purely multiplicative situationsOrder doesn’t matter in purely multiplicative situations
► Associative propertyAssociative property (a•b)c=a(b•c)(a•b)c=a(b•c) Grouping doesn’t matter as long as only multiplication is presentGrouping doesn’t matter as long as only multiplication is present
► Multiplicative Identity propertyMultiplicative Identity property a•1=aa•1=a Any number times 1 is the same numberAny number times 1 is the same number
The properties, cont.The properties, cont.
We have two new properties as listed below.We have two new properties as listed below.
We also add two important propertiesWe also add two important properties► Property of 0Property of 0
a•0=0a•0=0 Any number times zero is equal to zeroAny number times zero is equal to zero
► Property of -1Property of -1 a•(-1)=-aa•(-1)=-a Any number times -1 is the opposite of that numberAny number times -1 is the opposite of that number
This property is important
when we look at quadratics
ExampleExample
►What property is illustrated here?What property is illustrated here?
5(0) 0 A.Commutative
B. Associative
C.Identity
D.Propof -1
E.Prop of 0
ExampleExample
►What property is illustrated here?What property is illustrated here?
5(1) 1(5) A.Commutative
B. Associative
C.Identity
D.Propof -1
E.Prop of 0
ExampleExample
►What property is illustrated here?What property is illustrated here?
5( 1) 5 A.Commutative
B. Associative
C.Identity
D.Propof -1
E.Prop of 0
Practical ExamplePractical Example
► An investor purchase 50 shares of a stock at An investor purchase 50 shares of a stock at $3.50 per share. The next day, the change in $3.50 per share. The next day, the change in value of a share of the stock is -$.25. What is value of a share of the stock is -$.25. What is the total value of the shares the next day?the total value of the shares the next day?
.$ 12.50
.$12.50
.$162.50
.$175.00
A
B
C
D
Division DefinedDivision Defined
► It is helpful for us to look at division through It is helpful for us to look at division through the lens of fractionsthe lens of fractions
► All we did was multiply by the reciprocalAll we did was multiply by the reciprocal► This helps us because we can now use our This helps us because we can now use our
various rules and propertiesvarious rules and properties
3 2
4 5
3 5 15
4 2 8
Our ProcessOur Process► Let’s look at our process for doing divisionLet’s look at our process for doing division
16 116 4 16
4 4
66
1
To find the reciprocal we simply invert
the fraction
6 1
1 6
We also make the shift to
showing division as a
fraction
The Rules The Rules ►Same as MultiplicationSame as Multiplication►Because Division is nothing more than Because Division is nothing more than
the multiplication by the reciprocal our the multiplication by the reciprocal our rules of positives and negatives remainrules of positives and negatives remain Positive Positive • • Positive=PositivePositive=Positive Negative Negative • • Negative=PositiveNegative=Positive Positive Positive • • Negative=NegativeNegative=Negative
The RulesThe Rules► Similarly, when we change multiplication to division Similarly, when we change multiplication to division
we’re able to apply our properties of multiplicationwe’re able to apply our properties of multiplication Commutative PropertyCommutative Property Associative PropertyAssociative Property Identity PropertyIdentity Property Property of zeroProperty of zero Property of -1 Property of -1
ExampleExample
►Perform the arithmeticPerform the arithmetic
4 7
5 6
14.
1511
.3024
.1224
.35
A
B
C
D
The MeanThe Mean► Because of the use of division, the book also Because of the use of division, the book also
reintroduces the concept of the mean herereintroduces the concept of the mean here► We’ve spent some time discussing them already, so We’ve spent some time discussing them already, so
this topic should not be new to you.this topic should not be new to you.
ExampleExample
►Find the mean of the numbersFind the mean of the numbers
12,16, 19, 51 21
.2
. 10
49.
2.98
A
B
C
D
Practical ExamplePractical Example
► A large group leader orders 12 pizzas for A large group leader orders 12 pizzas for their group. If each pizza has 8 pieces and their group. If each pizza has 8 pieces and there are 22 people in the group. How there are 22 people in the group. How many pieces does each person get?many pieces does each person get?
.2
.3
.4
.5
A
B
C
D