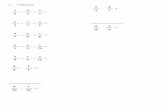Fracciones y decimales 6 docente

Matemát ica . Fracc iones y números decima les. 6º grado • Apuntes para la enseñanza 9

Desde que el Pre Diseño Curricular para el segundo c iclo comenzó a difundir-se, muchos docentes han planteado la necesidad de contar con materiales másvincu lados al traba jo del aula que los ayuden a interpretar los lineamientos cu-rriculares que se desarrollan en dicho documento. Más espec íf icamente, mu-chos docentes parecen considerar que las propuestas de cambio curricular enla Ciudad de Buenos apuntan a enriquecer la experienc ia educativa de losa lumnos a l tiempo que sol ic itan “mediaciones” entre esas formulaciones y lasprácticas del aula.

Por otro lado, en el marco del Plan Plurianual de Mejoramiento de la Ense-ñanza en el segundo ciclo, se ha identificado la dificultad de elaborar proyectosde enseñanza que articulen el trabajo matemático de un año a otro y hagan “cre-cer” la complejidad de contenidos que atraviesan el ciclo.

En esta serie, Fracciones y números racionales en el segundo ciclo, se ofrecenalgunas respuestas para estas cuestiones. Entre las muchas maneras en que sepodrían brindar algunas respuestas para las preocupaciones que nos ocupan atodos, se adoptó el criterio de realizar un material con propuestas analizadas deenseñanza y acompañarlo con páginas para el alumno donde se incluyen los pro-blemas propuestos.

Al presentar estas secuenc ias, la intención es mostrar cómo pueden losmaestros hacer evolucionar la complejidad de los contenidos que se proponen,ayudando a los a lumnos a tejer una historia en la que puedan transformar su“pasado escolar” –lo ya rea lizado– en una referenc ia para abordar nuevascuestiones, a l tiempo que cobran conc iencia de que progresan y de que son ca-paces de enfrentar cada vez asuntos más difíc iles (“esto antes no lo sabía yahora lo sé”).

Disponer de secuencias de enseñanza en las que se encara tanto el trata-miento didáctico de uno de los sentidos de un concepto para los distintos gra-dos del ciclo como de distintos sentidos de un concepto para un mismo grado,puede constituir un aporte para enfrentar el complejo problema de la articula-ción y la evolución de los contenidos a lo largo del ciclo.

Por otro lado, los docentes encontrarán en estos materiales situaciones “de re-paso” en las que se invita a los alumnos a revisar un tramo del recorrido escolar,proponiéndoles una reflexión sobre el mismo que “ponga a punto” su entrada enun nuevo tema. También son numerosas las apelaciones a hacer síntesis y a plan-tear conclusiones a propósito de un conjunto de problemas. Tal vez al principio

Introducción

G.C.B.A. • Secretaría de Educación • Dirección General de Planeamiento • Dirección de Currícula10

estas conclusiones estén muy contextual izadas en los problemas que les die-ron origen, será tarea del maestro hacer que se les atribuya un carác ter cadavez más general. El a lumno debe intervenir en el traba jo de articulación de lasdiferentes zonas del estudio de los números raciona les; para que pueda hacer-lo, el maestro debe convocarlo explícitamente a esa tarea y contribuir con élen su rea lización.

El material está organizado en actividades, cada una es una secuencia detrabajo que apunta a un contenido y que incluye varios problemas. En general sepresenta una pequeña introducción sobre los asuntos en juego en la actividad,se proponen problemas para los alumnos y se efectúa un análisis de los mismosdonde se ofrecen elementos para la gestión del docente. Muchas veces se sugie-ren, como parte del análisis de las secuencias, cuestiones nuevas para plantear alos alumnos. Es decir, el trabajo realizado por los alumnos en un cierto tramoofrece un contexto para plantear cuestiones más generales que no tendrían sen-tido si dichas actividades no se llevarán a cabo. Tomar como “objeto de trabajo”una serie de problemas ya realizados, analizarlos y hacerse preguntas al respec-to da lugar a aprendizajes diferentes de los que están en juego cuando el alum-no resuelve un problema puntual.

¿POR QUÉ UNA PROPUESTA SOBRE NÚMEROS RACIONALES?

En primer lugar, se trata de un campo de contenidos complejo, cuya elaboracióncomienza en cuarto grado y continúa más allá de la escuela primaria, que supo-ne rupturas importantes con las prácticas más familiares que los alumnos des-plegaron a propósito de los números naturales.

Como se explicita en el Diseño Curricular para la Escuela Primaria segundociclo:1

“El estudio de los números racionales –escritos en forma decimal o fracciona-ria– ocupa un lugar central en los aprendizajes del segundo ciclo. Se trata –tantopara los niños como para los maestros– de un trabajo exigente que deberá desem-bocar en un cambio fundamental con respecto a la representación de número quetienen los niños hasta el momento. Efectivamente, el funcionamiento de los nú-meros racionales supone una ruptura esencial con relación a los conocimientosacerca de los números naturales: para representar un número (la fracción) se uti-lizan dos números naturales, la multiplicación no puede –salvo cuando se multi-plica un natural por una fracción– ser interpretada como una adición reiterada,en muchos casos el producto de dos números es menor que cada uno de los fac-tores, el resultado de una división puede ser mayor que el dividendo, los númerosya no tienen siguiente...

“Por otra parte, como ocurre con cualquier concepto matemático, usos dife-rentes muestran aspectos diferentes. 2 Un número racional puede:

• ser el resultado de un reparto y quedar, en consecuencia, ligado al cocienteentre naturales;

• ser el resultado de una medición y, por tanto, remitirnos a establecer una re-lación con la unidad;

1 Para ampliar los difer-entes sentidos de las

fracciones, véaseMatemática, Documento

de trabajo nº 4 ,Actualización curricular,

G.C.B.A., Secretaría deEducación, Dirección

General de Planeamiento,Dirección de Currícula,

AÑO.

N OTA

Matemática . Fracc iones y números dec ima les. 6º grado • Apuntes para la enseñanza 11

• expresar una constante de proporcionalidad; en particular esa constante pue-de tener un significado preciso en función del contexto (escala, porcentaje,velocidad, densidad...);

• ser la manera de indicar la relación entre las partes que forman un todo; • etcétera.

Se considera entonces necesario trabajar con los docentes en la organizaciónde esta complejidad, proponiendo un desarrollo posible para la misma.

En segundo lugar, el Diseño Curricular plantea modificaciones al modo enque por años se concibió el tratamiento de los números racionales en la escue-la. ¿A qué tipo de cambios respecto de lo tradicionalmente instituido nos esta-mos refiriendo?

Al organizar los contenidos por “t ipos de problemas que abarcan distintossentidos del concepto” (reparto, medic ión, proporc iona lidad, etc.), el D i s e ñ oC u r r i c u l a r propone que se aborden en simultáneo asuntos que usua lmenteaparecían segmentados en el tiempo o, incluso, distribuidos en años diferentesde la escolaridad.

Por ejemplo, se inicia el estudio de los números racionales (las fracciones) apartir del concepto de división entera, proponiendo que los alumnos “sigan repar-tiendo” los restos de una división y cuantifiquen dicho reparto. Al dejar abierta laposibilidad de que el reparto se realice de distintas maneras, muchos a lumnosfracc ionan lo ya fraccionado y luego enfrentan el problema de cuant ificar esa ac-ción. Además, los diversos modos de hacer los repartos que surgen en la clase, dansentido a plantear la necesidad de establecer la equivalencia entre los númerosque representan esos repartos. Fracción de fracc ión y equivalencia aparecen en-tonces de entrada, aunque esos asuntos no se traten de manera formal sino en elcontexto en el que emergen. De modo que podríamos decir: que el problema dehacer repartos y establecer su equivalencia –problema que, como antes se seña-ló, se propone para abordar el estudio de las fracciones– “pone juntos” los conte-nidos de división entera, fracción, fracc ión de fracción, equivalencia y orden, a ltiempo que el mismo problema ofrece un contexto que da pistas para que losalumnos puedan tratarlos. En este último sentido, no diríamos, por ejemplo, quela noc ión “fracc ión de fracción” que surge de esta manera es exactamente la mis-ma que la que se trata cuando el tema se propone aisladamente. Aclaremos el al-cance de lo que seña lamos: de es, en cualquier contexto, ; lo que es-tamos subrayando es que el modo en que se plantea la necesidad de realizar di-cha operación –a partir de qué problemas, conociendo qué cuestiones– otorgarádiferentes sentidos a la misma, incluyendo en la idea de sentido los elementos quet ienen los alumnos para resolverla. Por otro lado, aunque del problema del repar-to equitativo surja la noción de fracción de fracción, ésta deberá ser retomada enotros contextos, retrabajada, descontextualizada y formal izada. Esto demandará,sin duda, mucho tiempo: como todos sabemos, las nociones no se aprenden deuna vez y para siempre sino que necesitan ser tratadas una y otra vez en distin-tos ámbitos y estableciendo relaciones entre ellas.

Sería legít imo preguntarse –muchos maestros lo preguntan–: “¿por qué com-plicar las cosas, si el trabajo ́ paso a paso´ da resultado?” La pregunta remite nue-vamente a la cuest ión del sentido que estamos atribuyendo a la matemática en

14

13

11 2


la escuela: desde nuestro punto vista, las nociones que estuvimos mencionando(fracción de fracc ión, equivalencia, reparto equitativo) están imbricadas unas conotras; por eso, tratarlas juntas en un contexto particular permite arrancar el es-tudio de las fracc iones con un conjunto más amplio y más sól ido de relacionesque se irán retomando con el tiempo. Tratar cada una de estas nociones de ma-nera aislada puede ser en el momento más fácil para los alumnos, pero, al sertambién más superfic ia l, se torna “menos duradera”. Menos duradera porque olvi-dan fácilmente aquello que no aparece entramado en una organización donde lasdistintas nociones que componen un campo de conceptos se relacionan unas conotras. Detrás de la idea de “lo fácil” y “lo difíc il” hay cuestiones importantes paradiscutir respecto de la experiencia format iva que se pretende impulsar.

Sintetizando: a l organizar el trabajo sobre los números racionales tomandocomo criterio los ámbitos de funcionamiento del concepto (reparto, medición,etc.), se modifica el orden de presentación que siempre tuvieron las noc iones queconforman el concepto. Aprovechemos para señalar que el paso del tiempo torna“naturales” c iertos ordenamientos de los contenidos escolares que en realidadfueron producto de decisiones que respondían a cierto proyecto educativo. Cuan-do se revisa el proyecto, lo natural es revisar también los órdenes y relaciones en-tre los contenidos.

Otro asunto que plantea el Diseño Curricular respecto de l tratami ento delos números rac ional es –y que se intenta plasmar en esta seri e– se refi ere a lpapel que se le otorga a las relac iones de proporc iona lidad como contexto enla elaborac ión de criterios para operar con fracc iones y decima les. Efectiva-mente , en las Páginas para el alumno de sexto grado que integran esta seriese presentan si tuaciones de proporc iona lidad dire cta donde hay que operarcon fracciones y dec imal es antes de haber formal izado y sistematizado los a l-goritmos correspondi entes a dichas operaciones. La idea es que los a lumnosresuelvan esas si tuaciones usando –a ve ces de manera implíc ita– las propie-dades de la proporc iona lidad y que , una vez resueltas, puedan ana lizar lo he-cho y tomar conc ienc ia de que en dicha resolución están involucrados cá lcu-los con fracc iones y decima les. Disponer del resultado de un cá lculo sin cono-cer el algoritmo obliga a pensar cómo debe funcionar el algoritmo para obte-ner un resultado que ya se conoce . En algún sentido, se está invitando a l si-guiente mecanismo productor de conocimiento: “si este problema involucra elcálculo x y yo ya resolví el problema y sé que el resultado es , aho-ra me las tengo que arreglar para entender cómo funciona la multipl icac iónde fracc iones para que x sea “. Obviamente no estamos esperan-do que los niños repitan frases de este tipo, sí queremos comunicar que esemec anismo está presente en el tratam iento de las operac iones mult iplic at ivascon fracciones y dec ima les; tenerlo en cuenta conlleva el doble propósito:ofrecer a los a lumnos un c amino para que elaboren estra tegias y opreren; y,de manera más transversa l, mostrar un mecanismo a través del cua l se pro-duce conocimiento matemát ico.

En tercer lugar, otra razón por las que se proponen materiales sobre los núme-ros racionales: quisimos mostrar la potencia de este contenido para poner en juegoaspectos del trabajo matemático a los que les atribuimos un alto nivel form a t i v o .

12

12

15

110

15

110

Matemá tic a . Fra cc iones y números decima les . 6º grado • Apuntes para la enseñanza 13

Formular leyes para comparar números, establecer la verdad o la falsedad deenunciados, analizar la equivalencia de expresiones numéricas sin apelar al cál-culo efectivo, comparar diferentes procedimientos realizados por “otros”, delimi-tar el alcance de diferentes propiedades (“esta ‘regla’ vale en tales casos”) sontareas que, al ubicar al alumno en un plano de reflexión sobre el trabajo llevadoa cabo, le permiten comprender aspectos de la organización teórica de la disci-plina, le posibilitan acceder a las razones por las cuales algo funciona de unacierta manera. Lograr que los alumnos adquieran cierto nivel de fundamentaciónpara los conceptos y propiedades con los que tratan, es un propósito de la edu-cación matemática que la escuela tiene que brindar.

CARACTERÍSTICAS DE LAS PROPUESTAS

Las secuencias que se presentan no están en general pensadas para que losalumnos resuelvan de manera inmediata la tarea que se les propone . Sí se es-pera -cada vez- que puedan empezar a abordar, explorar, ensayar. En a lgunoscasos, podrán arribar a conc lusiones de manera bastante autónoma y en otrosrequerirán de la ayuda del docente. Alentamos la tarea de exploración como unmodo de formar a un alumno autónomo, que acepta el desafío intelectual, queelabora criterios para validar su propio trabajo.

A propósito de algunos de los problemas, es probable que los alumnos eviden-cien cierta dificultad para entender con precisión qué es lo que se les pide. Puedeser que el docente interprete que el alumno no comprende la consigna. Sin embar-go, la falta de comprensión de la consigna se vincula en general con el hecho deque la tarea en danza es conceptualmente nueva; por eso, entender lo que se pidesupone para los alumnos ampliar su perspect iva respecto de los conceptos involu-crados en el problema. En esos casos seguramente serán necesarias explicacionesdel docente que “completen” la formulación escrita del problema. Estas explicacio-nes son un modo de empezar a comunicar las nuevas ideas que están en juego.

Se suele atribuir la falta de comprensión de las consignas a un tema “extramatemático” (más ligado al área de Prácticas del Lenguaje). Sin embargo, estafalta de comprensión es, en general, “matemática”: los alumnos no entiendenqué hay que hacer porque todavía no conciben claramente en qué consiste la ta-rea en cuestión. Comprenderlo es parte del aprendizaje.

Mucho se ha discutido si el docente debe o no intervenir en la tarea quereal iza el a lumno. Es cl aro que el docente debe ayudar a l alumno que se en-cuentra “bloqueado” eso hace a la def inición del trabajo docente . Ta l vez seabueno anal izar que entre “dec ir cómo es” y “no dec ir nada” hay una gama im-portante de intervenc iones que podrí an dar pistas a los a lumnos para seguirsosteniendo su tarea. Conocer dif erentes modos de abordar la tarea puedeayudar al docente a e laborar posibles intervenc iones. Ésa es la razón por lacua l, a l ana lizar las secuencias propuestas en Apunt es para la enseñanza, seinc luyen posibles estrategias de los a lumnos. La discusión de a lgunas de es-tas estrategias con el conjunto de la c lase podrá enriquecer el contenido quese está tratando, aunque las mismas no hayan sido propuestas por los niños.

Lograr que los alumnos entren en un trabajo matemático más profundo –máse n r i q u e c e d o r, pero también más difícil– no es tarea de un día, es producto de una


historia que se va construyendo lentamente en la clase. Los alumnos deben sen-tir que se confía en ellos, que tienen permiso para equivocarse, que su palabraes tomada en cuenta. A la vez deben aprender: a pedir ayuda identificando de lamanera más precisa posible la dificultad que tienen y no sólo diciendo “no mesale”, a respetar la opinión de los otros, a sostener un debate... El maestro juegaun rol fundamental en estos aprendizajes.

A diferencia de lo que suele pensarse, la experiencia nos muestra que mu-chos alumnos se posicionan mejor frente a un problema desafiante que frente auna tarea fácil. Lograr que el alumno experimente el placer de dominar lo que enun principio se mostraba incomprensible, ayuda a que construya una imagen va-lorizada de sí mismo. Obviamente, esto es bueno para él, pero también es alta-mente satisfactorio para el docente.

Es nuestro deseo que en alguna medida estos Apuntes para la enseñanza, ytambién las Páginas para el alumno, contribuyan a que el docente pueda enfren-tar la difícil tarea de enseñar, gratificándose con el despliegue de una prácticamás rica y más plena.


PRIMERA PARTE: FRACCIONES

A continuación se presenta una serie de problemas con el propósito de que losalumnos recuerden ideas vinculadas al concepto de fracción trabajadas en 4° y5° grado.

ANÁLISIS DE LOS PROBLEMAS 1, 2, 3 Y 4

A través de estos problemas se pretende repasar la definición de fracción que losalumnos han trabajado en años anteriores.

El problema 1 confronta a los alumnos con la necesidad de comparar la partea evaluar con el entero. Como no se puede cubrir el rectángulo con copias de la par-te sombreada, será necesario buscar un “intermediario” para establecer la medidade la parte sombreada. En este caso, el triangulito de la esquina puede resultar deutilidad ya que entra tres veces en la parte sombreada y ocho en el rectángulo to-tal; esto permite establecer que la parte sombreada es del rectángulo. En la dis-cusión colectiva puede señalarse que la estrategia de apelar a una parte del enteropara evaluar otra, resultará útil en los casos en los que se hace compleja la relacióndirecta entre esta otra parte y el entero.

Revisión del trabajo con fracciones 1

PROBLEMAS

1) Determinar qué parte del área del rectángulorepresenta la región sombreada.

2) ¿En cuál de los cuadrados se pintó más super-ficie? Tené en cuenta que los cuadrados soniguales.

3) En cada uno de los siguientes casos, el dibujorepresenta una fracción de la unidad. Para ca-da caso, tu tarea consiste en dibujar la unidad.

Representa de la unidad.



4 ) Si el área de la figura es de una cierta unidad,

dibujá una figura de área igual a la unidad. ¿Hayun único dibujo posible?

REVISIÓN DEL TRABAJO CON FRACCIONES

27

65

82

35

38


El problema 2 requiere comparar dos zonas. En este caso la vista parecee n g a ñ a r, ya que las dos áreas que se comparan son igua les aunque una pare-ce mayor que la otra. Establecer la igua ldad de las áreas requerirá anal izarque el tri ángulo “del medio” equiva le a los dos de los costados.

Reconstruir la unidad, a partir de conoc er sólo una fracción de ella, re-quiere diferentes relaciones en función de los números especí ficos del proble-ma. Así, en el primer caso del problema 3, los alumnos pueden intentar “jun-tar” varios dibujos como los dados, si bien esto no resultará sufic iente porque

+ + = . Si agregan otro dibujo, “se pasan”. Este mismo inten-to puede hacer observable que es clave conseguir que es la mitad de .Esto plantea otra cuestión: ¿cómo partir el gráf ico para representar ? Caeren la cuenta de que puede accederse a la solución de varias formas posiblesserá una oportunidad para diferenc iar f o r m a de m e d i d a.

El segundo gráf ico representa una fracc ión mayor que 1, razón por la cualel problema es a lgo más complejo que el anterior. Pero, justamente , la reso-luc ión del primer problema puede constituirse en un punto de apoyo: si se di-vide el rectángulo en 6, se obt iene , fracc ión que permite reconstruir có-modamente el entero. Es usual que , frente a un problema como éste, algunosa lumnos tiendan a dividir el rectángulo en cinco partes (en lugar de seis) porel hecho de que se trata de “quintos”. Será product ivo proponer esta discusióna l conjunto: “¿por qué si se trata de ‘quintos’ conv iene dividir el re ctánguloen seis partes igua les?”.

Al ana lizar el tercer gráf ico, los a lumnos deberán darse cuenta de que es equiva lente a 4, con lo cua l si toda la c ircunferenc ia representa 4 uni-

dades, la cuarta parte de la c ircunferencia equival e a 1. Resulta “raro” que ha-ya que dividir en partes para ha l lar la unidad. Ta l vez sea bueno explic itar es-ta “rareza” para habi litar con “pleno dere cho” el procedim iento.

Para anal izar el problema 4, en el cua l a partir de una f igura que repre-senta de la unidad se la busca recomponer, habrá que trabajar dos ide as:a) es necesario dividir en tres la f igura para obtener quintos del tota l; y b) ha-brá que considerar que no cua lquier división en tres partes garant iza terc iossino que se debe justif icar de a lguna forma que esas partes son igua les. Unamanera posible de abordar el problema sería dividiendo el hexágono en 6triángulos igua les con base en cada uno de los lados del hexágono y vért iceen el centro de la f igura.

De este modo, dos triángulos representarí an de la f igura y, por tan-to, de l a unidad que se debe reconstruir.

PROBLEMA

5 ) Resolvé los siguientes problemas:

a ) De un ramo de 12 flores, son rosas.¿Cuántas flores son rosas?

b ) Juan le regala la mitad de sus 68 figuritas aun compañero. ¿Cuántas figuritas le regala?

c ) Joaquín perdió de sus 30 f iguritas .¿Cuántas f iguritas perdió?


27

27

27

67 2

717

17

15

82

35

15

13

14 2

3

Ma temát ica . Fracc iones y números decima les. 6º grado • Apuntes para la enseñanza 17

ANÁLISIS DEL PROBLEMA 5

En este ítem se propone una serie de situac iones en las que es nec esario ave-riguar la fracc ión de una col ecc ión, como en el c aso de las situac iones a), b),c), d), o recuperar el entero conoc iendo la cant idad que corresponde a unaparte . Estas situac iones son simi lares a l as que los a lumnos enfrentaron a labordar el problema 3, si bien ahora se trata con cant idades discre tas, lo cua ll as hace algo más complejas. Esta mayor complejidad se debe a la necesidadde coordinar dos unidades simultáneamente: un objeto de la colecc ión y lacolecc ión entera.

Las primeras situac iones son más fác i les y ti enen la intenc ión de que losa lumnos “entren en ca lor” con el tema.

Averiguar la cant idad tota l conoci endo una fracción de la misma es unatarea un poco más compleja y requerirá que se revise con mayor profundidadel concepto de fracc ión. Así, por ejemplo, en el problema f) si se sabe que 32a lumnos representan de la cantidad tota l, podrían pensar que para ave-r iguar es necesario hacer 32 : 2. Y como 16 a lumnos representan de ltotal, para averiguar el entero, o sea, los , será ne cesario hacer 16 x 5, quees igua l a 80. En el espacio de la clase , resultará interesante comparar esteproblema con el problema 3 en el que los alumnos resolvieron una tarea si-m ilar usando magnitudes cont inuas.

En la última situac ión de esta serie de problemas, en la que se proponeaveriguar qué parte es 27 de 54, pueden surgir simultáneamente las fraccio-nes y .

Ta l vez sea un buen momento para discutir otros ejemplos y ll egar a laconc lusión genera l de que si se toman a objetos de una colección, cuyo totales de b obje tos, se t iene de la colecc ión. Seguramente esto deberá anal i-zarse con varios ejemplos y el docente eva luará l a pert inencia de proponer ono la notación con letras. Si decidi era hac erlo, deberá asegurarse de que losalumnos puedan establecer puentes entre la notación con letras y los ejem-plos numéricos.

d ) En el últ imo examen, de los 40 alum-nos obtuvo un puntaje superior a 6. ¿Quécantidad de alumnos tuvo esas notas?

e ) Martín de cidió regalar a su primo desus bolitas. Si le dio 23 bolitas a su primo,¿cuántas tenía?

f ) de los alumnos forman parte del equipode fútbol. Hay 32 alumnos en el equipo defútbol, ¿cuántos alumnos hay en total?

g ) María pegó 27 figuritas en su álbum. Si elálbum completo tiene 54 f iguritas, ¿quéparte del á lbum completó?

251

515

2754

12

55

ab

34

14

25


PROBLEMAS

6) Para cumplir con los pedidos del día, una con-fitería calcula que necesita usar 4 kg de hari-na. En el estante guardan 2 paquetes de

kg, 2 paquetes de kg y 2 de kg.¿Cómo podrías averiguar mediante un cálculomental si la harina que tienen es suficiente?

7) Respondé las siguientes preguntas:

a) ¿Cómo le explicarías a otro chico qué es ? ¿Y ?

b) ¿Qué es mayor ó ? ¿Por qué?

c) ¿Cuántos se necesitan para formar 2?

d) ¿Cuánto es la mitad de ?

e) ¿Cuánto es el doble de ?

8) Completá los espacios en blanco:

a) + .................... = 1

b) + .................... = 2

c) + .................... = 3

d) + .................... = 1

e) + .................... = 2

f) + .................... = 4

g) - .................... = 1

h) - .................... = 2

i) - ..................... = 1

9) Analizá qué numeradores o denominadores po-drían tener cada una de las siguientes fraccionespara que sean menores que 1 y cuáles podríant e ner para que sean mayores que 1. Anotáejemplos en los casilleros correspondientes:

10) Anotá estos números como una sola fracción:

a) 2 +

b) 5 +

c) 4 +

d) 10 +

e) 11 +

f) 8 +

11) Anotá estas fracciones como sumas de un nú-mero entero más una fracción menor que 1:

a)

b)

c)

d)

e)

f)

g)

h)

i)

j)

12) Indicá, en cada caso, cuál de las fracciones esla más cercana a :

a) ; ;

b) ;

c) ;

13) Decidí, sin averiguar el resultado, si es posible que

a) 3 - dé un resultado menor que 2

b) - sea menor que 2

c) + sea menor que 1

d) + sea mayor que 1

e) + sea mayor que

f) + sea mayor que 2

Para cada caso, pensá cómo explicar las razonesde tu respuesta.

5........

3........

........ 98


34

12

14

19

110

343434

Fracción a completar

Fracciones menores que 1

Fracciones mayores que 1

34

13

15

15

15

18

575757759494

23354637

410

85176

203229

294658623

581010210

115100

12

34

2323

23

45

13

15

14

14

52

75210210

25251719

2123

12

14

........ 4

........ 711

........

134........

25........


ANÁLISIS DE LOS PROBLEMAS 6, 7, 8, 9, 10, 11, 12 Y 13

El problema 6 propone sumar mentalmente diferentes cantidades. Una forma depensar esta suma sería agrupar primero cada uno de los paquetes de kg conlos paquetes de kg. Como hay 2 paquetes de cada una de las clases se obtie-nen 2 kg. Como, además, hay también 2 paquetes de kg se forman 3 kg.

Otra forma de pensarlo podría ser descomponer los paquetes de kg en kg + kg, y de esa manera asociar cada uno de los cuartos con los otros

paquetes de kg para tener kg.Así quedarían en tota l 6 paquetes de kg. Como cada 2 paquetes de

kg se obti ene 1 kg, hay en tota l 3 kg. La intención es que empiecen ac i rcular relac iones y resultados ya estudiados cuya disponibilidad será un pun-to de apoyo para avanzar.

El problema 7 apunta a recuperar conceptos vistos en años anteriores. Seesperan argumentos del t ipo:

• es l a fracc ión que entra 9 veces en el entero;

• es mayor que porque para formar un entero con tercios se ne-cesitan 3 partes iguales y en el caso de los quintos se necesitan 5;

• la mitad de es porque necesito 2 veces para tener .

Poner a los alumnos en situac ión de expl icar a un “otro” les exige selec-cionar cuá les son los aspectos que “arman” una explicación. Esto no es fáci l ytampoco puede ser elaborado por los a lumnos “en soledad”. Es a través de ladiscusión colectiva y de la intervención del maestro que se podrán ir estable-ci endo criterios comunes respecto de “qué es expl icar”.

Notemos que se pide una explic ac ión descontextua l izada. Aunque losa lumnos puedan ape lar a diferentes contextos para proponer sus expl icacio-nes, la intenc ión de la tare a es promover la idea de que l as fracc iones son nú-meros sobre los que se pueden establecer relaciones de manera independien-te de los contextos part iculares. Es éste también el objetivo de los problemass i g u i e n t e s .

El problema 9 ofrec e la posibi lidad de recuperar una regla seguramente yaestablec ida: se espera que los alumnos se den cuenta de que, si el denomina-dor es menor que el numerador, la fracc ión será mayor que 1. Los a lumnos de-berán, además, ocuparse de la cantidad de soluc iones posibles: cuando se tra-ta de completar el denominador, para formar una fracción mayor que 1, haytantas posibi lidades como números (natura les) menores que el numerador. Pa-ra formar una fracción menor que 1, el denominador puede ser cua lquier nú-mero mayor que el numerador. Por tanto, hay infinitas soluciones posibles.

Análogamente, se podrá ana lizar qué sucede cuando se trata de completarel numerador: existen inf initas soluciones para escribir fracc iones mayores que1 y una cantidad finita —tantas como números menores que el denominador—para escribir fracc iones menores que 1.

El problema10 retoma la posibil idad de expresar un número natura l comouna fracción de cua lquier denominador. Usando esa idea, 4 + podría pen-sarse así:

341

4 12 3

412 1

412 1

212

1913

15

15

15

110

110

14

35


como un entero son , esta expresión es equivalente a + + + + , o sea, .

Pero también podrían sistematizar que si 1 entero es igual a , en 4 enteros hay 4 veces ; 4 x es igual a .

Si a esto se le agregan los restantes, se obtiene la fracción .

El problema 11 supone ubicar en un primer paso la fracción entre 2 enteros obien pensar cuál es la mayor cantidad de enteros que se pueden formar, ya que es-to garantizará que la fracción restante sea menor que 1.

En el caso de , por ejemplo, se podría analizar que forman 1 entero y forman 2 enteros; por tanto, 1 es la mayor cantidad de enteros que se puede

f o r m a r. Para ello, se emplean 5 de los ; en consecuencia, = 1 + .El problema 13 ubica a los alumnos en posición de analizar la expresión para

establecer el valor de verdad de una proposición sin hacer el cálculo. Notemos quecuando tienen que hacer un cálculo se debe aplicar un procedimiento ya identifica-do. En cambio, en este caso los alumnos deben decidir por sí mismos qué relacionesestablecer para obtener una conclusión. Así, por ejemplo, para el ítem a) se esperaque analicen que, como es menor que 1, si a 3 se le resta , el resultado se-rá mayor que 2, ya que para obtener un resultado menor que 2 sería necesario res-tar a 3 una fracción mayor que un entero.

Es posible que los alumnos no tengan mucha práctica en la elaboración deesta clase de razonamientos. Para que el problema se constituya verdaderamen-te en una oportunidad de producir este tipo de relaciones, el maestro tendrá quefavorecer la circulación en la clase de las distintas propuestas de los alumnos,someterlas a la discusión de todos e intervenir él mismo proponiendo contrae-jemplos para las relaciones erróneas, sugiriendo ideas o preguntas, mostrandoeventualmente cómo piensa él algunos de los casos. La potencia de este ejerci-cio radica en la posibilidad de hacer análisis similares al descripto y explicitar es-tos análisis como lo propone la segunda parte del ejercicio.

El total de los problemas propuestos hasta acá se concibe como un modo dedifundir en la clase muchas ideas que los alumnos han tratado en años anteriores.Sin embargo, no es cuestión solamente de recordar lo que los alumnos ya sabían.Volver a revisar estos conceptos supone también hacer nuevas relac iones, volvermás densa la trama de cuestiones a las que estos conceptos pueden dar lugar.

Al finalizar la actividad se pueden anotar colectivamente los aspectos trabajados:

• fracción de una colección,• obtención del entero conociendo una fracción de éste,• fracciones mayores y menores que 1,• ubicación de una fracción entre dos enteros,• expresión de un número entero como una fracción,• estimación de resultados de sumas y restas con fracciones.

55

55

85

85

85

105

55

55

55

55

55

55

55

35

35

35

235

205

235

23

23


Con esta actividad se propicia el surgimiento de estrategias para ordenar una se-rie de fracciones, ubicar las fracciones entre enteros y, por último, interpolar unafracción entre dos fracciones dadas.

ANÁLISIS DE LOS PROBLEMAS 1, 2, 3, 4 Y 5

Los problemas 1 y 2 en los que la cuestión es ubicar fracciones entre dos ente-ros, pueden ser resueltos por los alumnos si descomponen la fracción como la su-ma de fracciones equivalentes a números enteros más la fracción restante. Estose apoya en algunos de los problemas de la actividad 1.

Tomemos la cuestión de ubicar . Este número puede ser pensado como + + ; o sea, como 2 + ; lo cual autoriza a decir que está entre

2 y 3. A su vez, el anál isis de esta estrategia puede l levar a establecer un proce-

dimiento más económico. Por ejemplo, para , ¿cuántas vec es entra 4 en 11 ?Entra 2 veces enteras, para lo cua l “usé” 8 de los 11 cuartos en cuestión, res-tando aun . Esto permite expresar más directamente como suma de

+ . La pregunta “¿cuántas veces entra?” se resuelve matemáticamente con una di-

visión; en efecto, 11 dividido 4 tiene cociente 2 (los enteros que se pueden formar)y resto 3 (los cuartos que no llegan a formar otro entero). Se ve que este caminoarticula estrategias más “artesanales” con el conocido procedimiento de dividir elnumerador por el denominador para expresar una fracc ión como número mixto.

PROBLEMAS

1) Estos números se encuentran entre 0 y 3. Ubi-calos en la columna que corresponde., , , , ,1 , , , ,

2) ¿Entre qué números enteros se ubican las si-guientes fracciones?

, , , , , ,

3) Encontrá si son posibles las fracciones que acontinuación se detallan y si no fuera posibleexplicá por qué:

• una fracción con denominador 3 entre 0 y 1

• una fracción con denominador 5 entre 4 y 5

• una fracción con numerador 1 entre 0 y 1



4) La siguiente lista de fracciones está ordenada demenor a mayor. ¿Dónde ubicarías ? ¿Y 1 ?

5 ) Intercalá una fracción entre cada par de números:

1

Relación de orden entre fracciones 2

RELACIÓN DE ORDEN ENTRE FRACCIONES

Entre 0 y 1 Entre 1 y 2 Entre 2 y 3

34

12

57

25

35

65

45

47

54

128

158

197

12512

612

34

34

84

34

37

83

45

114

2135

57

95

145

119

177

474

283

337

95

8512

12510

849

114 11

4

114

114

44

44

34


Será interesante hacer notar a los alumnos que la forma “número mixto” permiteubicar rápidamente la fracción entre dos enteros. De manera transversal se difun-de una idea potente para el trabajo matemático actual y futuro: algunas escritu-ras muestran aspectos de un cierto objeto que otras no muestran tan claramente.

El problema 3 tiene sentido si se da un tiempo suficiente de exploración; nohay “chances” de que los alumnos respondan “de entrada”.

Para el primer caso, al buscar fracciones con denominador 3 es probable quelos alumnos vayan ensayando: , , , ... Se espera que reparen enque no vale la pena continuar la serie pues ya es equivalente a 1 y las otrasfracciones con denominador 3 son mayores que 1. Por tanto, hay 2 fraccionescon denominador 3 entre 0 y 1. Se hace notar que el problema pone a los alum-nos en situación de obtener una conclusión referida a un conjunto infinito: detodas las fracciones con denominador 3, las únicas que están entre 0 y 1 sony . Esta es la riqueza que se le atribuye al problema: producir un argumentoque permita estar seguro, sin ensayar caso por caso.

Para ubicar fracciones entre 4 y 5 con denominador 5, “conviene” expresar el4 y el 5 como fracciones con denominador 5, de esta manera 4 es equivalente a

y 5 es equivalente a . No se trata de un problema de respuesta inmedia-ta para los alumnos. Si el docente decide plantearlo en la clase, deberá prever untiempo importante de exploración. A nuestro juicio ese trabajo de exploración esen sí mismo productor de nuevas relaciones y, en ese sentido, el tiempo invertido“vale lo que cuesta”.

Los dos últimos ítemes del problema 3 son bastante más complejos, el do-cente decidirá si los propone o no.

En ninguno de los casos es posible encontrar fracciones con las condicionesque se piden. Por ejemplo, no es posible encontrar fracciones con numerador 2entre 3 y 4, ya que es equivalente a 1 y a medida que “se agrandan" los de-nominadores la fracción se aleja cada vez más del 1, achicándose.

Nuevamente los alumnos se ven en situación de producir un argumento queasegure una conclusión sobre un conjunto infinito, ya que no es posible la ex-ploración caso por caso.

Los problemas 4 y 5 reinvierten todas las estrategias utilizadas acerca de lasequivalencias y la comparación de fracciones.

En el problema 4, una posible estrategia para ubicar dentro de una serie defracciones ya ordenadas es ir comparándola con cada una de las fracciones. La pri-mera fracción es menor que un medio ya que 1 entero es equivalente a .La mitad de es igual a y medio quinto más. Más exactamente, la mitad de

es igual a + . La fracción que sigue es . Si se sigue el mismo razo-namiento anterior, la mitad de es + ; por tanto, se ubica entrey .

En el problema 5 probablemente no será un obstáculo intercalar una frac-ción entre y . A la hora de hacerlo, entre y será necesario bus-car fracciones equivalentes que permitan la interpolación de fracciones. No se-ría extraño que en una primera instancia los alumnos piensen que el problemano tiene solución, sobre todo en este caso en el que aun pensando a como

, no es posible hallar una fracción con denominador 4 entre y . Elmaestro podrá plantear la necesidad de seguir trabajando con las equivalenciasanalizando, por ejemplo: cómo es la fracción en relación con las fracciones da-

12

12

12

34

34

12

23

205

22

255

13

13

33

33

43

25

24

24

55

55

55

25

252

5110

47

47

37

114

77

35

65

23

58

Matemá tic a . Fra cc iones y números dec ima les. 6º grado • Apuntes para la enseñanza 23

das. La idea es comenzar a analizar que siempre se pueden intercalar fraccionesentre dos dadas. Entra aquí en juego la noción de densidad, noción difícil, de ela-boración muy lenta y acerca de la cual este problema constituye apenas una pri-mera aproximación. Será interesante señalar la diferencia entre esta situación yla que se plantea en el problema 3: entre dos fracciones dadas, existen infinitasfracciones (caso que se plantea en el problema 5) pero, si se impone alguna otracondición (como en el problema 3), puede ser que haya una cantidad finita defracciones o ninguna fracción.

Como se señala en Matemática. Fracciones y números decimales. 5º grado.Apuntes para el docente, la representación de fracciones sobre la recta numéri-ca constituye un ámbito sumamente fructífero para poner en juego las relacio-nes construidas sobre estos números: como recurso para comparar fracciones,para determinar entre cuáles enteros se encuentra una fracción, para proponerfracciones entre otras dadas, para representar sumas y restas. Sin embargo, de-bemos partir de reconocer la dificultad que supone para los alumnos compren-der esta representación. Efectivamente, para representar fracciones sobre un ejedeben comprender por qué los números se anotan no sólo ordenados sino con-servando una cierta escala que puede variar de una representación a otra. Tam-bién será necesario que comprendan que dicha escala se determina fijando la po-sición del 0 y del 1 o, más generalmente, fijando la posición de dos números cua-lesquiera.

Resulta también dif ícil para los alumnos la idea de que un punto representa unnúmero y ese número a la vez representa la distancia al 0 en la escala elegida.

Notemos que en las representaciones iniciales de fracciones, cuando un en-tero está dividido en partes iguales, cada parte representa el mismo número:

En cambio, en la recta, el primer tramo es , el segundo y el tercero ; o sea, 1.

Será importante contrastar estos aspectos con los alumnos como un modo decontribuir a la comprensión de esta forma de representación.

Por otra parte, también es difícil aceptar que un punto (un número) admitediferentes escrituras.

Más adelante se llegará a la generalización de que números racionales equi-valentes tienen la misma ubicación en la recta numérica.

Dada la complejidad que acabamos de señalar, proponemos iniciar el trabajocon rectas numéricas partiendo de situaciones que las contextualicen para des-contextualizar posteriormente los conocimientos así construidos.

Fracciones en la recta numérica 3

13

13

13

13

23

33


FRACCIONES EN LA RECTA NUMÉRICA

12

12

12

16

23

0

1 km 5 km12

175

133

23

36

312

56

3535

M 1 km P

1 km

FRACCIONES EN LA RECTA NUMÉRICA

C D A B

C D E G F

H

PROBLEMAS

1) El club Luna de Avellaneda organizó una carrera. Pondrán algunos carteles que indiquen a los corre-dores qué parte del recorrido llevan ya realizado. A continuación, aparece una representación de la pis-ta y de los lugares donde quieren ubicar los carteles. (Véase Páginas para el alumno, pág 16, Línea de12 cm, carteles de largada y “llegada”; los carteles en blanco están ubicados a , , del re-corrido.)

a) Completá qué deberían decir los carteles en blanco.

b) Un grupo de chicos pensó en hacer una broma a los corredores y poner muchos de esos cartelessobre la pista: ¿dónde ubicarías otros carteles que dijeran ; ; ; ; ?

c) Proponé ubicaciones de carteles para que tus compañeros digan qué deberían decir. Intercámbienselos.

2) Se organizó una maratón de 5 km. A continuación aparece una representación del recorrido. (Segmen-to de 15 cm de largo, con 0 –en el extremo izquierdo– y 1 –a 3 cm– marcados. Además, algunos pun-tos indicados: A a 6 cm; B a 7,5 cm; C a 2,5 cm; D a 5 cm.)

a ) ¿Dónde ubicarías carteles que indiquen: km; km; km?

b ) ¿Qué deberían decir los carteles ubicados en los puntos que aparecen señalados?

3 ) A continuación aparece una representación de una ruta que va desde la ciudad A hasta la ciudad B. A lolargo del camino, aparecen carteles indicadores de la distancia del cartel hasta la ciudad A.

¿Qué deberían decir los carteles ubicados en los puntos señalados?

4) A continuación una ruta que va desde una ciudad M hasta una ciudad P. (Segmento de 9 cm con M yP en los extremos, y los siguientes puntos marcados: a 1 cm del extremo izquierdo debe decir “1 km”;C a 0,5 cm del extremo izquierdo; D a 5 cm; E a 6 cm; F a 8 cm y G a 7,5 cm.)

¿Dónde irían ubicados los siguientes carteles?

5) Esta es la representación de otra ruta que parte desde la ciudad H y llega hasta la ciudad Z. En la ru-ta se marcan las distancias (en km) hasta la ciudad H.

a) ¿Dónde habría que marcar la ciudad Z si se encuentra a 4 km de H?

b) ¿Dónde ubicarías un cartel que dijera “2 km”?

6 km

12

km 9 km

5 km

23

16

14

13

34

1 km 5 km

A BE C D

Matemát ic a . Fracc iones y números decima les . 6º grado • Apuntes para la enseñanza 25

ANÁLISIS DE LOS PROBLEMAS 1, 2, 3, 4, 5 Y 6

Como primer punto en el anál isis colectivo de las resoluc iones se expl ic ará quela línea que a ll í aparece es una representac ión de la pista hecha a escala, esdecir que la longitud de la pista rea l y la del dibujo no son las mismas, peroque sí se conservan las relaciones entre las distancias de los diferentes carte-les en ambas pistas: la rea l y la representada.

Será necesario que los alumnos comprendan qué signif ica que “se conser-van las relaciones”. Por ejemplo, si en la rea lidad una distancia es el doble dela otra, esta relac ión debe conservarse en la representac ión.

Para completar los carteles en la pr imera pista, cuest ión propuesta en elproblema 1 a) puede establecerse la medida que existe entre la largada y la lle-gada, medida que corresponde al total de la pista, o la medida que correspon-de a la distanc ia entre la largada y la mitad de la pista. Esto da lugar a dos ra-zonam ientos diferentes: la distanc ia entre la largada y el primer cartel entra 4veces en el tota l; o sea, que el primer cartel indica de la carrera.

Pero también puede establecerse que la distanc ia entre la largada y el pri-mer cartel entra 2 veces entre la largada y la mitad de la carrera, de maneraque esa distanc ia es la mitad de , o sea, .

Del mismo modo, la distancia entre la largada y el segundo cartel que sedebe completar entra 3 veces en el tota l de la recta, por tanto el segundo car-tel debería dec ir . Pero también podría considerarse la distancia entre elcartel que marca y este nuevo cartel. Esta distancia entra 12 veces a lolargo de toda la pista, en consecuencia es . Así, el segundo cartel se en-cuentra a + ; es decir, a de la pista que equiva le a de ella.

Las relac iones anteriormente expuestas pueden ser un punto de apoyo pa-ra ubicar las fracciones que se proponen en el problema 1 b).

Antes de establecer la ubicación precisa, será interesante pedir que los alum-nos la anticipen globalmente. En estas anticipaciones se producen relaciones queayudan a elaborar estrategias para representar la fracción. Por ejemplo, para ,podrán establecer que está entre y 1, y que está más cerca de 1 porque sólole falta para alcanzarlo. Para determinar la ubicación, podrán hallar la longi-tud de y luego contar 5 de estas partecitas desde 0 o contar hacia atrás unasola desde 1. A propósito de la discusión sobre la ubicación de , se podrá so-licitar a los alumnos que propongan otras maneras de nombrar ese punto.

En el caso del problema 2, en la discusión colectiva se retomarán las rela-ciones establecidas a propósito del problema 1). El doc ente podrá preguntar por

14

12

14

14

14

12

1121

12412

13

13

56

16

16

3535

6) Esta es la representación de otra ruta que parte desde la ciudad J y llega hasta la ciudad K. ¿Dóndeubicarían el cartel de la ciudad que está a “1 km” de J y el cartel que indica la ciudad K que está a3 km de J?

J

65 km

210


qué, en el problema 1, aparecía marcado a los 6 cm y aquí a 1,5 cm delpunto de part ida. Deberá quedar c laro, por un lado, que son representac ionesconstruidas a diferente esca la y, por otro, que se trata de unidades diferentes(la tota lidad del recorrido en el primer caso; un kilómetro en el segundo).

Esta actividad se centra en la producc ión de criterios para comparar fraccio-nes. Probablemente en los grados anteriores los alumnos hayan desarrolladoalgunas estrategias, más o menos generales. Muchas veces las estrategias quese ponen en juego dependen de los números en cuestión. Se propone ahoraavanzar sobre este aspec to, alentando a los alumnos a que encuentren nuevasestrategias.

La discusión sobre la va lidez de dist intos criterios para comparar fraccio-nes es el último punto de la actividad. Se busca promover un trabajo sobre re-glas generales a partir del análisis de criterios parciales que, en principio, no sepusieron necesariamente en juego con una perspectiva de generalidad. Esta po-sición en la que los alumnos analizan un tramo de lo realizado para sintetizarloen un conjunto de leyes generales contribuye a que tengan una perspectiva ca-da vez más general. Éste es uno de los aspectos formativos del trabajo matemá-tico que se busca.

PROBLEMAS

1) Proponé 2 fracciones menores y 2 fraccionesmayores que , y explicá cómo llegaste a esaelección.

2) Proponé 2 fracciones menores que y 2 frac-ciones mayores que .

3) Un ferretero tiene dos frascos con clavos delmismo tipo. En uno de ellos , la e tique ta dice

kg y en el otro la etiqueta dice kg.¿Qué frasco contiene más clavos?

4) En los supermercados frecuentemente tienenbolsas de fruta de diferentes pesos. La mamáde Nico quería hacer dulce y necesitaba kgde manzanas.¿Cuáles de las siguientes bolsas de manzanaspuede comprar Nico seguro de que a su mamále alcanzarán para hacer el dulce?

kilogramos

kilogramos

kilogramos

5) Indicá con el signo mayor (>); menor (<) óigual (=):

a)

b)

c)

d)

e)

f)

g)

h)

Relación de orden entre fracciones. Otra vuelta4

RELACIÓN DE ORDEN ENTRE FRACCIONES. OTRA VUELTA

12

141

4

34

78

910

457623

2518

2510

1545

816

936

1240

4748

3435

7590

2815

35100

2510

1632

4080

1222

1430

12

Matemá tic a . Fracc iones y números decima les . 6º grado • Apuntes para la enseñanza 27


A través de los primeros cuatro problemas se busca promover la producción decriterios “locales”, es decir, criterios útiles para esas fracciones pero no necesa-riamente aplicables a cualquier par de fracciones. Esta idea de poner a los alum-nos a analizar cada situación justamente intenta alentar la producción de rela-ciones que profundicen su relación con el tema.

Al pedirles que busquen fracciones mayores y menores que y mayores ymenores que (problemas 1 y 2) pondrán en juego criterios basados en la re-lación entre el numerador y el denominador, que después serán útiles para com-parar otros pares de fracciones.

Por ejemplo, una vez establecido que, si el numerador de una fracción es ma-yor que la mitad del denominador, la fracción es mayor que , se podrá usaresta relación para comparar otras fracciones con respecto a ; por ejemplo,para comparar y , la primera es mayor que y la segunda es menor,con lo cual es mayor que .

Los alumnos también encontrarán en esta actividad los límites que tienen al-gunos de los criterios usados ya que son útiles en algunos casos y no en otros.Por ejemplo, en el problema 3, es posible comparar con si se establececuánto falta en cada caso para el 1: al primer frasco le falta kg para comple-tar el kg y al segundo le falta menos porque le falta de kg. Se establece en-tonces que es mayor que porque está más cerca de 1.

Sin embargo, este criterio no sería conveniente para comparar fracciones co-mo y , donde comparar lo que les falta para llegar al entero tiene la mis-ma dificultad que comparar las fracciones originales.

En el problema 5 se ponen en juego diferentes criterios: comparar con ócon 1, establecer cuánto falta para 1, simplificar las fracciones para luego com-pararlas, establecer una relación entre el numerador y el denominador, etc. Estáclaro que no todos los alumnos usarán los mismos criterios en cada caso y estojustamente enriquece el problema.

A continuación, se presentan dos problemas que el docente podría proponerluego de trabajar los anteriormente mencionados con el objetivo de apuntar aconclusiones generales respecto de la comparación de fracciones.

121

4

121

2

12

122212

22

1430 14

30

78

78

910

910

110

18

47

59

12

ANÁLISIS DE LOS PROBLEMAS 6 Y 7

El problema 6 invita a la explicitación de los criterios usados y el problema 7apunta a que los alumnos establezcan su alcance. En la discusión, el docente de-berá tener presente que muchas veces para los alumnos es difícil reconocer unaregla como inválida aunque sólo se cumpla para algunos casos particulares.

Una forma de completar este trabajo sería detenerse en los casos que sirvenparcialmente: por ejemplo, considerar entre qué enteros se encuentran las frac-ciones es útil cuando las fracciones que se comparan se hallan entre diferentesenteros.

Además de mostrar contraejemplos, el docente necesitará volver a resaltarque el tamaño de una fracción depende de la relación entre el numerador y eldenominador y no de considerarlos aisladamente.


PROBLEMAS

6) En los ejercicios anteriores encontraron mu-chos pares de fracciones para comparar.Hagan una lista de reglas que sirvan para com-parar fracciones.

7) Un grupo de chicos anotó una serie de reglaspara comparar fracciones. Señalá cuáles te pa-rece que

• sirven siempre,• sirven parcialmente, • no sirven nunca.

En cada caso, explicá por qué

RELACIÓN DE ORDEN ENTRE FRACCIONES. OTRA VUELTA

¿Les parece que esta reglasirve para comparar

f r a c c i o n e s ?

1 ) Considerar sólo entre quéenteros se encuentran.

2) Si dos fracciones tienenigual denominador, es mayor la que tiene mayor numerador.

3) Si dos fracciones tienen el mismo numerador, esmayor la que tiene menord e n o m i n a d o r.

Siempre Parcial-mente

Nunca

¿Les parece que esta reglasirve para comparar f r a c c i o n e s ?

4) Si las dos fracciones se encuentran entre los mismos enteros, convieneconsiderar a qué distanciaestán del entero o de otrafracción del entero, como

ó ; etcétera.

5) Si una fracción tiene su numerador mayor que sud e n o m i n a d o r, es seguro queserá mayor que otra frac-ción que tenga su numerador menor que sud e n o m i n a d o r.

6) Para comparar fracciones sepueden buscar fraccionesequivalentes a las que setrata de comparar; o sea,que tengan el mismo d e n o m i n a d o r, y aplicar laregla 2.

7) Si una fracción tiene el numerador y el denominador mayores quelos de otra, seguro es mayor. .

Siempre Parcial-mente

Nunca

12

14


En esta actividad se propone recuperar las estrategias de cálculo vistas en añosanteriores en relación con la suma y la resta de fracciones.


A partir de la resolución de estos problemas se espera hacer un recorrido de lasestrategias utilizadas por los alumnos para sumar y restar fracciones y recupe-rar un procedimiento general para sumar y restar fracciones.1 El procedimientopropuesto transforma las fracciones que intervienen en el cálculo en fraccionesequivalentes del mismo denominador.

Las relaciones de proporcionalidad directa constituyen un ámbito a partir del cual re-pensar aspectos sobre el funcionamiento de las fracciones. En particular brindan uncontexto en el que apoyarse para resolver operaciones de multiplicación y división defracciones por números naturales (y de números naturales por fracciones).

Para abordar estos problemas es conveniente que los alumnos puedan partir de lasiguiente idea: en una relación de proporcionalidad directa se cumple que al doble deuna cierta cantidad le corresponde el doble del correspondiente de dicha cantidad, altriple le corresponde el triple y, en general, cuando una de las cantidades se multipli-ca o divide por un número, la cantidad correspondiente se multiplica o divide por elmismo número. Es claro que no se espera esta formulación por parte de los alumnospero sí se requerirá que sean capaces de poner en juego estas relaciones.

Los siguientes problemas apuntan a que los a lumnos traten la mult ipl ica-c ión y la div isión de fracc iones por un número natura l, apoyados en contextosque favorecen la puesta en juego –seguramente impl íc ita– de propiedades dela proporcionalidad directa.

PROBLEMAS

1) Un corredor se entrena en una pista. Él afirmaque en la primera etapa de la carrera recorrió

de la pista, y en la segunda y última etaparecorrió los restantes. ¿Es esto posible?

2) De una jarra que cont iene 2 litro de aguallené dos vasos de litro cada uno y un va-so de de litro. ¿Cuánta agua quedó en laj a r r a ?

3) A Juan le proponen que elija la bolsa de golosi -nas más pesada. La primera bolsa pesa 3 kgy la segunda pesa kg. ¿Cuál pensás que ha-brá elegido Juan? ¿Cuánto pierde si elige mal?

4) ¿Cuánto hay que agregar a para obtener?

5) ¿En cuánto excede a ?

Multiplicación y división de una fracción por un número natural

6

OPERACIONES CON FRACCIONES

Operaciones con fracciones 5

34 1

4

13

14

12

34

1 Algunas de ellas seencuentran analizadas enMatemática. Fracciones ynúmeros decimales. 5ºgrado. Apuntes para laenseñanza.

206

45 7

925

13


ANÁLISIS DE LOS PROBLEMAS 1 Y 2

Los problemas anteriores ponen en juego la multipl icac ión de un número na-tural por una fracc ión. Se trata de relaciones de proporcional idad dire cta enlas que la constante de proporc iona lidad es un número fracc ionario que se“apl ica” a un número natural (cant idad de porc iones para la tabla 1, cant idadde personas para las tabl as 2 y 3, y cant idad de pasos para la tabla 4).

La idea es alentar a los alumnos a que primero vayan completando los casi-lleros más fáciles. Tomemos, por ejemplo, la tabla 1: para 6 personas (el doble de3) se necesitará el doble de litro, o sea, l itro. El cá lculo para 2 personasse puede resolver haciendo la tercera parte de lo que se necesita para 6 personas;es decir, la tercera parte de litro. También se puede establecer la cantidad

PROBLEMAS

1 ) Completá las siguientes tablas:

Tabla 1

Esta tabla relaciona la cantidad de leche ne-cesaria para la receta de un flan, según lacantidad de porciones que se desea obtener.Para esta receta se calcula litro de lechepara 3 porciones.

Tabla 2

Esta tabla relaciona la cantidad de personasinvitadas a un asado con la cantidad de carneque habrá que comprar. Para el asado se calcula

kg de carne cada 3 personas.

Tabla 3

En otro asado, ca lculan kg de carne cada3 personas.

Tabla 4

La siguiente tabla relac iona la distancia querecorre un robot de juguete según la cant idadde pasos que da. El robot da pasos de dec e n t í m e t r o .

2) Dos amigos discuten acerca de la cantidad deachuras necesarias para 6 personas sabiendoque se ca lculan kg cada 4 personas.

El primero piensa lo siguiente:

• La mitad de es , por lo tanto, para6 personas hacen falta + ó .

• La otra piensa así:

• La mitad de es y la mitad dees . Eso es lo que necesito por perso-na, entonces para 6 personas necesito6 x = .

¿Son correctos ambos procedimientos? ¿Cómojust ificás tu afirmación?

Cantidad de porciones

Leche necesaria(en litros)

10 8 5 6 2 3

Cantidad de personas

Cantidad d ecarne necesaria(en kilos)

2 3 4 6 8 10


Cantidad decarne necesaria(en kilos)

2 3 4 6 8 10

Cantidade de pasos queda el robot

Distancia querecorre (en cm)

1 5 10 12

70 100 200

200 1 . 0 0 0

75

MULTIPLICACIÓN Y DIVISIÓN DE UNA FRACCIÓN POR UN NÚMERO NATURAL

14

14

12

12

34

34

34

34

34

34

14

12

12

38

38

38

383

16

316

1816

98

75


ne cesari a para 2 personas, si se ca lcula primero l a cantidad para 1 persona( :3) y luego el doble de esa cantidad. Puede ser que los a lumnos necesitenun tiempo para hac er estos cá lculos, pero es importante que el maestro sepaque ellos han podido elaborar a través de los distintos problemas todos loselementos para real izarlos y para probar si los resultados que proponen son ono vá l idos.

Es importante que l as diversas estrategias posibles para completar las ta-blas “se acompañen” con los correspondientes cá lculos sobre fracc iones. Po rej emplo, de las dos maneras seña ladas para establecer la cantidad de lechenec esaria para dos personas, surgen los siguientes cá lculos:

: 3 = ; o bien

: 3 = ; x 2 = =

Para contribuir a que los alumnos e laboren estrategias de control, es fun-damenta l que el docente seña le que , por cua lquiera de estos dos caminos, losr e s u ltados deben ser iguales, y que un modo de pensar el problema debe servirpara verificar los cálculos que se corresponden con otro modo de pensarlo. La ri-queza de relaciones que surgen es la fuente de elaboración de estrategias paraoperar con números rac ional es.

El docente podrá sugerir que se reúnan por parejas para comparar los re-sultados obtenidos y las estrategias que emplearon. También, pueden pasar enl impio todos los cá lcu los con fracciones que surgieron al completar las tablascon sus correspondientes resultados.

Pedir a los a lumnos que encuentren la mayor cantidad de cálculos quesurgen de las tablas t iene por objet ivo poner en funcionamiento ese doblejuego entre el contexto particular, las relaciones de proporc iona l idad y lasoperac iones con números raciona les. Se trata de que comprendan que, aun-que no sepan las cuentas de una manera sistemat izada, pueden de todos mo-dos obtener los resultados graci as a lo que saben del contexto.

Una vez que las tablas se han completado, será necesario analizar global-mente cada una. La idea es establecer que, en cada tabla, se “pasa” del renglónde arriba al de abajo, multipl icando por un número fracc ionario. Así, para latabla 1, la cant idad de leche necesaria para una porc ión de flan es , resul-ta entonces que mult iplicando la cantidad de porc iones por se obt iene lacorrespondiente cant idad de l eche . Esta conclusión es el resultado de un aná-l isis de la tabla ya hecha por caminos más “artesana les” y diversos, y no unacondic ión previa para completarla. Justamente lo que se quiere comunicar esque los alumnos disponen de un conjunto de relac iones de base que permi tenavanzar en la comprensión de los cá lculos para luego sistematizar una estra-tegia general .

12

112

112

16

16

212

14

1121

12

14


ANÁLISIS DE LOS PROBLEMAS 3, 4 Y 5

Estos tres problemas ponen en juego la división de una fracción por un núme-ro natura l. En las pr imeras tablas se trata de relaciones de proporc iona l idaddirecta con constante fracc ionaria “apl icada” a números natura les. Ahora setrata de div idir fracc iones por un número natural. La secuencia está pensadadel siguiente modo: primero se completa una tabla, después se anal iza unatabla ya comple ta para establecer cuá l es la constante que transforma un nú-mero en su correspondi ente y fina lmente se pide a los alumnos que propon-gan una tabl a dada la constante de proporc iona l idad.

La primera de estas tareas es la más fácil y pone c laramente en juego l adiv isión de una fracc ión por un número natura l.

La segunda tarea es conceptualmente mucho más compleja: ya no se tratade hacer un cálculo sino de analizar un conjunto de pares para establecer unaregularidad entre ellos: cuál es la operación (siempre la misma) que aplicada a

da , aplicada a da , aplicada a da , etc. Se trata de uncambio de posición del alumno: debe inferir una relación analizando un conjun-to de datos. Seguramente el docente deberá señalar que esta tarea se relacionacon la anterior pero es diferente; una vez realizada será importante establecercon los alumnos semejanzas y diferencias entre los problemas 3 y 4.

Para el problema 5, es importante que el maestro insista en que puedenproducirse tablas que tengan números dist intos y que eso no signif ica que es-tén mal confe cc ionadas. Los chicos no están habituados a decidir qué núme-ros forman parte de los datos de un problema. Por lo genera l, en la tradic ióne s c o l a r, esta es una atribuc ión del maestro, como también el he cho de adju-dicarle , a un único enunc iado para todo el grupo, los mismos va lores. Será in-teresante en este caso ana lizar con los alumnos que , a pesar de ser númerosdistintos, se cumplen l as mismas relac iones en cada tabla y que eso permiteestar seguros de que está bien hecha.

Sería conveniente sintetizar todas las relaciones producidas hasta el mom e n t o

PROBLEMAS

3) Laura, Aníbal y Julieta se pusieron de acuerdo:al terminar la fiesta dividirían el resto de latorta en tres partes iguales, una para cada uno.Completá la siguiente tabla que relaciona lafracción de torta que recibirá cada uno, segúnla cantidad de torta que sobró en la fiesta:

4) La siguiente tabl a es pare c ida a la anterior,pero en este caso no se sabe entre cuántos

am igos se repartió l a torta que sobró. ¿Po d é sa v e r i g u a r l o ?

5) Ahora armá una tabla como la anterior en laque la torta que sobra se reparte entre 5 ami-gos. Tenés que decidir qué números pondrás enla tabla. Seguramente tus compañeros no deci -dan incluir los mismos números que vos; eso nosignifica que las tablas estén mal.

Fracción de torta que sobró en la fiesta

Fracción de torta para cada uno

14

13

Fracción de torta que sobró en la fiesta

Fracción de torta para cada chico

116

13

18

112

1

MULTIPLICACIÓN Y DIVISIÓN DE UNA FRACCIÓN POR UN NÚMERO NATURAL

12

14

12

14

14

14

12

18

13

112

116


sobre operac iones con fracc iones, poniendo en discusión las formulacionesimprec isas, las relaciones erróneas, l as distintas maneras que han surgido pa-ra expresar una m isma cuestión, etc. Será út i l que los a lumnos vuelvan sobresus primeras versiones y recojan los elementos ya ident if icados con toda lac lase.

A partir de la div isión de fracc iones de forma por un número natura l —asunto que se ha tratado part icularmente en los problemas 3, 4 y 5—, se es-pera que resuelvan otras divisiones apl icando o bien rel ac iones de proporc io-na lidad direc ta (por ejemplo, si se tripl ic a la fracc ión, se triplic a el coc iente),o bien descomponiendo la fracc ión que se divide en suma de fracc iones deforma y aplic ando la propiedad distributiva de la división respecto de lasuma, o bien aplicando esta propiedad a alguna otra descomposición conve-niente de la fracc ión.

Por ejemplo, para : 2

• a partir de : 2 = , será posible establecer que : 2 = 3 x ( : 2) = .

• Como = + + ,: 2 = : 2 + : 2 + : 2 = + + = .

• Como = +: 2 = : 2 + : 2 = + .

Algunas de las af irmac iones que podrían quedar registradas:

• Para dividir una fracción de numerador 1 por un número natural, mult ipli-co e l denominador por el número natural. Por ejemplo, : 3 = .

• Para dividir una fracc ión por un número natural “me conviene” apoyarmeen una fracción de numerador 1.

• La mult ipl icación de una fracc ión por un número natura l se puede pensarcomo una suma de varias fracciones igual es.

• E t c é t e r a .

Estos problemas intentan una primera aproximación a la multiplicación de fraccio-nes basada en las relaciones de proporcionalidad directa, continuando el trabajo quese realizó para la multiplicación y la división de fracciones por un número natural.

Estas relaciones ya fueron tratadas en la actividad anterior en la que se es-tablecían relaciones entre números naturales y fracciones. El avance que ahora sepropone es el de relacionar fracciones con fracciones. Efectivamente, en esta secuen-cia se incluirán tablas de proporcionalidad con constante fraccionaria con la inten-ción de apoyarnos en este contexto para validar los resultados de diferentes opera-ciones e ir identificando así un procedimiento general para multiplicar fracciones.

Multiplicación de fracciones en el contexto de la proporcionalidad directa

7

14

1n

1n

37

37

27

27

114

114

114

114

114

314

314

37

37

373

7

17 1

7

17

17

17

17

17

17

17

1717

112


Una pregunta legítima que el docente puede hacerse es acerca del sentidode plantear un trabajo tan complejo cuando el algoritmo de la multiplicación defracciones es “sencillo” y podría usarse una estrategia más económica para en-señarlo. Nuestra respuesta frente a esto es que la actividad propuesta apunta aque el alumno acceda a una cierta fundamentación del algoritmo de la multipli-cación y no sólo a su mecanismo.


Es rel at ivamente sencil lo establecer a esta a ltura que la relac ión que subyacea la tabla es kg de helado por persona. Completar una primera tabla sen-ci lla permite ident ificar una serie de cálculos y da lugar a que los a lumnos con-soliden el “juego” de reconocer cálculos una vez completada la tabla.

En este caso se puede identificar que

4 x = 1

8 x = 2

2 x =

1 x =

Eventualmente el docente podrá proponer otros cálculos referidos al mismocontexto, que no se hayan incluido en la tabla.

PROBLEMA

1 ) Completá la siguiente tabla que vincula la cantidad de helado que es necesario comprar en función delos invitados que asistirán a una fiesta, sabiendo que para cada invitado se calcula la misma cantidad.

Cantidad de personas invitadas

Cantidad de helado que es necesario comprar (kg)

4 8 2

1 14

MULTIPLICACIÓN DE FRACCIONES EN EL CONTEXTO DE LA PROPORCIONALIDAD DIRECTA

14141414

1214

14

Matemát ic a . Fracc iones y números decima les . 6º grado • Apuntes para la enseñanza 35


A partir de las relaciones de proporcionalidad conocidas por los alumnos, es po-sible completar los diferentes casi lleros de esta tabla. Por un lado, queda ident ifi-cado que la constante de proporcionalidad es de litro por kilómetro. Esto sig-nifica que, para obtener el correspondiente de una cierta cantidad de k ilómetros,“basta” multiplicar esa cantidad por la constante de proporcionalidad. Ahora bien,los alumnos no podrían en principio utilizar este procedimiento para hallar el co-rrespondiente de porque no han aprendido aún a mult iplicar fracciones (parahallar el correspondiente de tendrían que multiplicar x ). Sin embargo,están en condiciones de establecer el correspondiente de : el correspondien-te de es , por tanto, el correspondiente de es . De estas conside-raciones se deduce que x tiene que dar . Será este un buen momen-to para proponer otros valores de modo que los alumnos enfrenten distintas mul-tiplicaciones de fracciones. Podrían, por ejemplo, hallar la cantidad de nafta ne-cesaria para recorrer km, km, etcétera.

Para que la resolución de este problema sea posible tiene que estar disponi-ble en los alumnos el cálculo de la mitad, la tercera parte, la cuarta parte, etc.de una fracción, trabajado en la actividad anterior.

Las relaciones establecidas se pueden sintetizar en una tabla como la si-guiente:

PROBLEMA

2) Completá la siguiente tabla que relaciona los kilómetros recorridos por un automóvil y los litros decombustible que consume, sabiendo que el automóvil tiene siempre el mismo consumo por cadakilómetro que recorre.

Kilómetros que se recorren

Litros de nafta que se utilizan

1 2 3 12

32

110

Kilómetros que se recorren

Litros de naftaque se utilizan

1 2 3 12

32

110


x 2 x 3 : 2x 3

x 3: 2

x 3x 2

12

210

310

120

320

110

110

110

32

32

32

32

32 3

2120 3

20

320

35

43

GCBA • Secretaría de Educación • Dirección General de Planeamiento • Dirección de Currícula36

Los cálculos involucrados en este caso son:

1 x =

2 x =

3 x =

x =

x =


Nuevamente, se pone en juego el recurso de completar la tabla apelando a dife -rentes procedim ientos, para ident if icar luego las mult ipl icaciones por

(constante de proporcionalidad) que surgen del análisis de la tabla. Es así co-mo se puede calcular la cantidad de azúcar necesaria para 1 kg de fruta dupli-cando la que se precisa para kg de fruta: ó que es el doble de .Para kg de fruta se puede recurr ir a la mitad de la cantidad de fruta nece-saria para kg; o sea, a la mitad de que es . Para conocer la cant i-dad de azúcar que se prec isa para kg de fruta, bastará mult iplicar por 3 lacantidad necesaria para kg; esto es, 3 x = , etcétera.

Una vez completada la tabla se puede analizar con los alumnos las diferen-tes multiplicaciones que surgen:

x = 1 x =

x = x =

x = 2 x = =

x = x =

PROBLEMA

3) Para realizar una receta, por cada kg de fruta, hacen falta kg de azúcar. Completá la siguien-te tabla para poder saber qué cantidad de cada ingrediente es necesaria, según el caso.

Cantidad de fruta (en kg)

Cantidad de azúcar (en kg)

1 2

116

38

34

32

94

18


12

14

121

4

14

12

1232

341

4

14

14

14

14

34

12

14

14

14

14

14

14

12

12

110

110

110110

110110

120320

210310

18

28

18

18

38

32

38

316

332

94

916

18

116

116

116

316

24

Matemá tic a . Fra cc iones y números dec ima les. 6º grado • Apuntes para la enseñanza 37


Este problema presenta una complejidad mayor que los anteriores, porque laconstante de proporcionalidad ( litro de agua por cada kilogramo de polvo)no es, como en aquellos, una fracción de numerador 1. Los alumnos enfrentanentonces el desafío de multiplicaciones de fracciones más complejas. Para esta-blecer el correspondiente de 1, podrán calcular el doble de , que es ó .Para establecer el correspondiente de , deberán establecer cuánto es la cuar-ta parte de . Un modo de pensarlo es considerar que la cuarta parte de es

y, por tanto, la cuarta parte de es . El correspondiente de es tresveces ; o sea, .

Una vez identificados los cá lculos involucrados, se podrá empezar a reco-noc er que para hacer la tercera, la cuarta, la quinta parte de una fracción, semultiplica el denominador por 3, 4, 5 y, para hacer el triple, el cuádruplo, elquíntuplo de una fracción, se multiplica el numerador por 3, 4, 5, etc. Estasideas empezarán a hacer observable una regla que el maestro deberá expl icarapoyado en las act ividades anteriores.

El producto de dos fracciones es otra fracción con numerador igual alproducto de los numeradores de las fracciones dadas y con denominador igualal producto de sus denominadores.

Por ejemplo:

x = =

PROBLEMA

4) Las siguientes instrucciones corresponden a unpolvo para preparar pintura: “Para conseguir elcolor exacto, mezcle kilogramo de polvopor cada litro de agua”.

- ¿Qué cantidad de agua es necesaria para 1 kgde polvo?

- ¿Qué cantidad de agua será necesaria para kg de polvo?

- ¿Qué cantidad de agua debe utilizarse parakg de polvo?

En todos los casos debe obtenerse siempre elmismo tono de color, como lo detallan las ins-trucciones.

Si te ayuda, podés construir una tabla de pro-porcionalidad como la siguiente, con valoresque te sirvan para averiguar lo que te pide elproblema:

Cantidad de polvo(en kg)

Cantidad de agua (en litros)

1 14

34

34


12

14 1

2

341

4

64

12

34

35

27

3 x 25 x 7

635

34

34

32

32 3

2

32

18 9

838

38



Es posible averiguar la cantidad de mermelada que se obtiene con 1 kilo de fru-ta haciendo la quinta parte de 3, esto es . Para averiguar la cantidad corres-pondiente a kg de fruta, hay que establecer cuánto es la mitad de . Estose puede pensar así: la mitad de es , por tanto, la mitad de es

. Probablemente la relación más difícil de establecer es la que correspondea kg de fruta. Podría entonces usarse como paso intermedio, de lafruta se corresponde con la tercera parte de la cantidad que se obtiene con 1 kgde fruta, : 3 = , por tanto, si con kg de fruta se obtiene , conse obtendrá .

Queda planteada así la operación x = .

De la misma forma que en el caso anterior también puede buscarse la cons-tante de proporcionalidad de la tabla que sería el número por el cual hay quemultiplicar a 5 para llegar a 3; o sea, .

SEGUNDA PARTE: NÚMEROS DECIMALES

Los números dec imales no son un asunto nuevo para los alumnos. Sin embargo, esprobable que, pasado un tiempo, se hayan olvidado de algunas relaciones con lasque es interesante contar para continuar profundizando el estudio. Por esa razónproponemos una situación de repaso que permita explicitar un “piso común” a par-tir del cual retomar el trabajo. Será necesario recordar lo siguiente:

• la estructura posiciona l de la notac ión decima l: cada c ifra representa unafracc ión decima l de la unidad mul tipl icada por el va lor de esa c ifra;

PROBLEMA

5) En la siguiente tabla se muestra la relación entre cantidad de fruta que se usa para hacer mermela-da y la cantidad de mermelada que efectivamente se obtiene. Completala.

Cantidad de fruta (kg)

Cantidad de mermelada (kg)

5 1 23

3

Repasamos cuestiones básicas de los números decimales1


12

12

35 3

5 35

35

35

15

1103

10 13

23

23

23

13

13

315

315

315

615

615

Matemática . Fracc iones y números decima les. 6º grado • Apuntes para la enseñanza 39

• las relaciones de valor entre posiciones contiguas (10 veces 0,1 es 1; 10 ve-ces 0,01 es 0,1; etcétera);

• la multiplicación por 10, 100, 1.000, etc., sobre la base de las relaciones an-teriores.

ANÁLISIS DE LOS PROBLEMAS 1, 2, 3, 4, 5 Y 6

En un primer momento el docente puede recordar a los alumnos que los númerosdecimales son una manera de anotar las fracciones con denominador 10, 10 0 ,1.000, etc. Como una primera actividad previa a la resolución de la tabla, el docen-te puede proponer a los alumnos un trabajo por parejas en el que deban ponersede acuerdo sobre el modo de anotar ciertos números.

3) Apoyados en los cálculos anteriores, realicenahora estos cálculos:

0,2 x 10 = 0,2 x 100 =

1,2 x 10 = 1,2 x 100 =

0,02 x 10 = 0,02 x 100 =

1,02 x 10 = 1,02 x 100 =

1,22 x 10 = 1,22 x 100 =

4) Ya sabés que de una multiplicación siempre sepueden extraer dos divisiones. Por ejemplo, si sesabe que

1,2 x 10 = 12, se sabe también que 12 : 10 = 1,2; y que 12 : 1,2 = 10.

Anotá todas las divisiones que surgen del pro-blema 3.

5) Escribí reglas para multiplicar por 10 y por 100un número decimal.

6) Es muy fáci l recordar que, si se reparte $ 1 entre10 personas, cada una recibe 0,10 y que esto“lleva” al cálculo 1 : 10 = 0,1. De la misma ma-nera $ 1 repartido entre 100 (aunque sea raro)da 0,01, lo cual nos permite recordar el cálculo1: 100 = 0,01.

¿Cuánto es 0,1 : 10? Explicalo usando las rela-ciones anteriores.

REPASAMOS CUESTIONES BÁSICAS DE LOS NÚMEROS DECIMALES

Notación decimal (en $)

0,50

0,25

0,10

2,25

0,05

3,05

2,80

2,8

Notación fraccionaria (en $)

PROBLEMAS

Seguramente el año pasado estudiaste númerosdecima les. Puede ser que no recuerdes del todo al-gunos de los asuntos estudiados y, por eso, empe-zaremos ahora con un repaso.

1) Anotá, usando fracciones y considerando elpeso ($) como unidad, las siguientes cantida-des de dinero, expresadas en decimales.

2) ¿Cuánto dinero (en $) hay en 10 monedas de10 centavos? ¿Y en 10 monedas de 1 centa-vo? ¿Y en 100 monedas de 1 centavo? ¿Y en100 monedas de 10 centavos?De las cuestiones anteriores surgen algunoscálculos:

0,10 x 10 = 0,01 x 100 =

0,01 x 10 = 0,1 x 100 =


Para la resolución de la primera tabla, tal vez el docente necesite asegurarsede que los alumnos comprenden qué significa usar el peso como unidad, y para esoquizá sea conveniente clarificar que las mismas cantidades de dinero se podríanexpresar en centavos, usando números enteros. La relación entre el peso y el cen-tavo será la clave para que los alumnos resuelvan la tarea. Una vez realizada, seráimportante identificar que la segunda cifra de la notación decimal corresponde alos “décimos de peso” aunque en términos de sistema monetario no tenga nombrepropio.

Se espera que, a partir de expresar las cantidades de dinero en fracciones,se pueda explic itar el valor de c ada una de las cifras en la notac ión dec ima l.Por ejemplo:

0,25 = + ; 2,25 = 2 + +

Por otro lado, las dos últimas líneas de la tabla serán una oportunidad para se-ñalar la equivalencia entre 2,8 y 2,80; y, en general, se podrá hablar del efecto deagregar ceros al final de la notación decimal, contrarrestándolo con el de agregarceros intermedios.

Se comienza el trabajo con números decimales en el contexto del dinero. Laidea es que dicho contexto sirva de punto de apoyo para explicitar las relacionesde valor entre posiciones contiguas, primero referidas a cantidades de dinero y lue-go descontextualizadas, tal como se propone en los problemas 2, 3, 4 y 5. Sobre labase de esas relaciones de valor, se justifican las reglas para multiplicar y dividirpor 10 y por 100. Luego, esas mismas relac iones se pueden hacer extensivas a lasmultiplicaciones por otras potencias de 10.

En los problemas que se proponen a continuación se analizará el valor posicionalde las cifras en las escrituras decimales, las equivalencias entre las posic iones con-tiguas y no contiguas de la escritura decimal y las operaciones subyacentes a lasescrituras decimales.

Valor posicional2

PR O B L E M A S D O N D E “V A L E” L A C A L C U L A D O R A

1) Si sólo se pudieran apretar las teclas“0”; “1”; “.” ; “+” de la calculadora: a) ¿Cómo podrían escribirse los siguientes

números? Anotá en tu carpeta la cuentaque harías.

0,2; 0,03; 0,005; 0,25; 0,375; 341,406

b) Para anotar un número, Juan sumó 3 veces0,001; 3 veces 0,1 y 4 veces 0,01. ¿Qué nú-mero anotó?

c) Intentá armar 1,02 de dos maneras diferen-tes. ¿Y 1,2?

VALOR POSICIONAL

5100

5100

210

210


AN Á L I S I S D E L O S P R O B L E M A S 1, 2, Y 3

En los problemas donde se utiliza calculadora será necesario que el docente expliqueque en el uso de los números decimales se emplea la coma para separar la parteentera de la decimal; sin embargo, en la calculadora se representa con un punto.

Nuevamente en la puesta en común será interesante analizar que 10 veces unaunidad de un orden equivale a 1 vez la unidad del orden inmediato superior. Ta m-bién, a partir de estas actividades, podrán iniciarse ciertas equivalencias multiplica-tivas. Por ejemplo, para formar 0,2, es posible sumar dos veces 0,1 o hacer 20 veces0 , 01, etcétera.

Para el problema 2 se espera que primero los alumnos realicen anticipaciones,que se expliciten en la puesta en común y se discutan, para luego verificarlas conla calculadora. Será necesario aclarar que en la calculadora deberán hacerlo condos cálculos parciales (las multiplicaciones) que luego se sumarán.

En el problema 3 es necesario explicitar el valor de las cifras que deben ser mo-dificadas en función de su valor posicional. Es decir, en el 2,347 el 3 correspondea 0,3, que es necesario borrar, o sus equivalentes 0,30 ó 0,300, en cuyo caso es in-teresante advertir por qué al anotar estos últimos números se borran de la calcu-ladora los últimos ceros.

Por ejemplo, se podría dejar registrado, lo siguiente:

cada lugar después de la coma vale sucesivamente 0,1; 0,01; 0,001; 0,0001; etc. Así, por ejemplo, el número 12,158 equivale a:

1 x 10 + 2 x 1 + 1 x + 5 x + 8 x

o, lo que es lo mismo:

1 x 10 + 2 x 1 + 1 x 0,1 + 5 x 0,01 + 8 x 0,001

d) ¿Qué número se arma sumando 10 veces0,1; 10 veces 0,01 y 10 veces 0,001? Antici-palo antes de verificarlo en la calculadora.

2) R e s p o n d é :a ) ¿Qué número se arma haciendo

5 x 0,1 + 3 x 0,01 ?

b) ¿Qué números se forman haciendo los si-guientes cálculos?

4 x 0,1 + 3,001 + 5 x 0,001

7 x 0,1 + 6 x 0,001

2 x 0,01 + 5 x 0,001

c) Propongan cálculos similares para que rápi-damente un compañero pueda dar el núme-ro e intercámbienlos.

3) Resolvé los siguientes problemas:

a ) Si en el visor de la calculadora escriben el nú-mero 3,452, ¿qué cálculo hay que hacer en lamáquina para que aparezca el número 3,402sin borrar? ¿Y para que aparezca 3,052?

b) Si en el visor de la calculadora está el nú-mero 2,347, ¿qué deben hacer para queaparezca el número 2,007 sin borrar?

11.000

1100

110


AN Á L I S I S D E L P R O B L E M A 4

A raíz de 4 a) se pueden promover las siguientes relaciones: ¿qué modificaciones seproducen en un número al agregarle 0,1?; ¿cuál es la cifra que cambia?; ¿porqué?; ¿cuándo cambia más de una cifra en la escritura del número?; ¿por qué?En 4 b) este análisis se extenderá a los centésimos.

En 4 c) y 4 d), además, deberán anticipar, a partir de analizar la escritura delnúmero, cuántos centésimos se necesitan para completar los décimos a fin de al-canzar el próximo entero.

En 4 d) se extienden estas relaciones a las equivalencias entre milésimos, centé-simos y décimos. Aquí, en el análisis posterior a su resolución, deberá explicitarse que,si para un décimo se necesitan diez centésimos, como cada centésimo se forma condiez milésimos, para un décimo se necesitan cien milésimos. Este análisis podrá que-dar anotado en las carpetas junto con escrituras que lo expresen, por ejemplo:

0,1 = 10 x 0,010 , 01 = 10 x 0,0010,1 = 10 x 10 x 0,001 = 100 x 0,001

Entonces, agregar 0,4 a un número es lo mismo que agregar 4 veces 0,1 ó 40 ve-ces 0,01 ó 400 veces 0,001 .

En el siguiente problema se reutilizan las relaciones trabajadas respecto dela descomposición de un número en décimos, centésimos y milésimos, pero estavez a propósito de la resta.

c) Si a 124,77 le sumás 0,01 y seguís apretan-do “=”, ¿qué números irán apareciendo?

¿Cuántas veces hay que sumar 0,01 parallegar a 125?

d) Si queremos ir de 13,6 a 14 sumando de a0,01, ¿cuántas veces habrá que apretar latecla “=”?

¿Y si lo hiciéramos sumando de a 0,001?

VALOR POSICIONAL


4) Pensando con la calculadora.a) Si anotás en la calculadora 29,8; sumás 0,1

y seguís apretando la tecla “=”, se suman0,1 cada vez que volvés a apretar “=”.

Anotá qué números irán apareciendo siapretás 5 veces la tecla “=”.

Después, verificalo con la calculadora.

b) ¿Y si a 29, 8 le sumás 0,01?


Los siguientes problemas permiten poner de manifiesto la estrecha relación entre nú-meros decimales y el sistema métrico decimal. Es importante que el docente tenga encuenta que ambas nociones se alimentan mutuamente.

Para que los alumnos puedan abordar los siguientes problemas, será necesario quetengan presentes las unidades de longitud del sistema métrico decimal.

El análisis de la escritura y la lectura de las medidas de longitud debería llevar adiscutir con los niños, por ejemplo, que la expresión 4,6 metros “esconde” el hecho deque el 6 a la derecha de la coma representa en este caso 6 décimos de metros y estoequivale a 6 decímetros; o que 4,25 km corresponde a 4 kilómetros más 0,25 km, queson 2 décimos de km (es decir, 2 hm) + 5 centésimos de km (es decir, 5 dam).


En el análisis colectivo, se busca establecer que de metro es una longitud tal que10 veces esa longitud es 1 metro.

O sea, 1 m : 10 = m = 0,1 m

Es decir, se vuelven a retomar aquí los análisis de las escrituras decimales desa-rrollados en el contexto del dinero, ahora a propósito de las unidades de longitud.

Esto es 1: 10 = porque 10 veces es 1.


5) Siguiendo con la calculadora.a ) Ahora anotamos en la calculadora el nú-

mero 1,7. Queremos ir restando reiterada-mente 0,1 hasta llegar a 0. ¿Cuántas veceshay que restar lo? Recordá que primerodeberás resolverlo y recién luego podrás ve-rificarlo con la calculadora.

b ) Si anotamos 2,45, ¿cuántas veces hay querestar 0,01 para llegar a 2? ¿Y para llegar a 0?

PROBLEMA

1) Resolvé:a) Si partimos una tira de un metro en 10 partes iguales, ¿cuál es, en metros, la longitud de cada

parte? ¿Y en centímetros?

VALOR POSICIONAL

UNIDADES DE LONGITUD

c ) Si anotamos 0,351, ¿cuántas veces habríaque restar 0,001 para l legar a 0? ¿Y paral legar a 0,3?

d ) Si anotamos 4,206, ¿cuántas veces habrí aque restar 0,001 para l legar a 4? ¿Y paral legar a 4,2?

Unidades de longitud 3

110

110

110

110


ANÁLISIS DEL PROBLEMA 1 (CONTINUACIÓN)

Las relaciones establecidas a partir del problema anterior podrán expresarse a travésde las siguientes escrituras:

m = 0,01 m = 1 cm

m = 5 x 0,01 m = 0,05 m = 5 cm

Los siguientes problemas extienden estas relaciones a los milésimos y a diferen-tes conversiones entre metros y centímetros. Podrá observarse que la conversión deuna unidad de medida a otra no se establece a partir de la presentación y el uso me-cánico de un conjunto de reglas, sino del análisis de las equivalencias.

PROBLEMAS

2) Ya estudiaste que de metro es una longitudtal que 1.000 veces esa longitud equivale a unmetro. de metro se escribe también 0,001metro. Un milésimo de metro es un milímetro.

a ) ¿Cuántos milímetros tiene 1 metro? ¿Y uncentímetro? ¿Qué parte de un centímetro esun milímetro?

b) ¿A cuántos centímetros equivale una lon-gitud de 0,001 metros? ¿A cuántos milíme-tros equivale esa misma longitud?

c ) ¿A cuántos centímetros equivale una longi-tud de 0,111 metros? (Acordate de que 0,111es lo mismo que + + )

3) Seguí resolviendo.

a ) ¿Qué parte de un metro son 40 centímetros?

b) Completá usando números decimales:

40 cm = ........... m

c) ¿Qué parte de un metro son 123 cm?

d) Completá usando números decimales:

123 cm = ........ m

e ) Completá la siguiente tabla que relaciona lon-gitudes expresadas en centímetros con esasmismas longitudes expresadas en metros.


PROBLEMAS

b) Esta tira mide de metro. Es decir quemide 0,01 metro.

¿Cuántas tiras necesitaríamos para armaruna tira de 1 metro? ¿A cuántos centímetrosequivale 0,01 metro?

c ) ¿Cómo se escribe en números decimalesde metro?

d ) ¿Cuántos cent íme tros tiene una t ira dede metro? Acordate que de me-

tro se escribe tambi én 0,5 metro.

e ) ¿A cuántos centímetros equiva le una lon-gitud de 0,05 metros? ¿Y una de 0,55 me-t r o s ?

f ) ¿Cuántos cent ímetros tiene una tira de 5,5m e t r o s ?


1100

5100

5100

5100

510

1100

11.000

11.000

1100

110

11.000


ANÁLISIS DE LOS PROBLEMAS 2, 3, 4, 5, 6, 7 Y 8

Se recordará aquí el aná lisis y las conclusiones previas a l traba jar con núme-ros decima les.

Hay varias maneras de pensar la mitad de 0,5 metros:

• La mitad de 0,5 metros puede pensarse a partir de la mitad de 0,1 metros.

Como la mitad de 0,1 es 0,05, la mitad de 0,5 es 5 x 0,05; es decir, 0,25.

• 0,5 metros es lo mismo que 0,50 metros, la mitad es 0,25 metros.• 0,5 es metro. La mitad de metro es m, es decir, 25 cm; o sea,

metros ó 0,25 metros.• 0,5 = 0,4 + 0,1. La mitad de 0,4 es 0,2 y la mitad de 0,1 es 0,05; por tan-

to, la mitad de 0,5 es 0,25.

f) ¿Qué cuenta hay que hacer para expresaren centímetros una longitud que está ex-presada en metros? ¿Y para expresar enmetros una longitud que está en centíme-tros?

g) Anotá todas las cuentas de multiplicar por100 y de multiplicar por 0,01 que surgen dela tabla anterior.

4) Con lo trabajado hasta ahora, respondé:

a ) ¿A cuántos centímetros equivalen 3 milíme-tros? ¿Y 30 milímetros? ¿Y 300 milímetros?¿Y 0,3 milímetros? ¿Y 0,03 milímetros?

b) Completá las siguientes tablas que relacio-nan longitudes expresadas en diferentesunidades:

5) Una tira mide 4 metros 60 centímetros de lar-go. ¿Cuáles de las siguientes escrituras expre-san esa cantidad?

4,060 m

460 cm

4,6 m

4 m 60 dm

6 ) Para pasar por cierto túnel, es necesario que losvehículos tengan como máximo una altura de2,20 metros. ¿Cuáles de los siguientes vehículospodrán pasar?

A: 207 cm

B: 2 m 30 cm

C: 2 m 1 dm

D: 2 m 10 dm

E: 2,10 m

7) Un automóvil recorre una distancia de 5 km 80m y otro recorre 5,8 km. Decidí si ambos reco-rrieron lo mismo.

8) Respondé:

a) ¿Cuánto es la mitad de 1 metro? ¿Y la mitadde 0,5 metros? ¿Y la mitad de 0,05 metros?¿Y la mitad de 0,4 metros? ¿Y la mitad de0,3 metros?

Longitud en metros

Longitud en centímetros

2,3 2,03 2,003 2,33

5 12 102 1 0,5

L o n g i t u den centímetros

L o n g i t u den milímetros

0,4 0,02 0,42

30 5 35 3 1 0,5

Longitud en metros

Longitud enm i l í m e t r o s

1

1

10

10 100

0,1 0,01 10 , 11

111

3,5

0,5 0,05

25100

14

12

12


Las distintas estrategias ponen de relieve diferentes relaciones entre los nú-meros decimales al tiempo que informan a los alumnos acerca de modos de va-lidar las conclusiones que van obteniendo. Un análisis similar podrá hacerse pa-ra establecer la mitad de 0,05 metros.

AN Á L I S I S D E L O S P R O B L E M A S 8, 9 Y 10

Estos últimos problemas constituyen una oportunidad para volver sobre la multiplica-ción y la división de números decimales por 10 y para revisar las razones que justifi-can las reglas, ya identificadas, de “correr la coma”.

En esta oportunidad, se elaborarán criterios para comparar números decimales.

Comparación y orden de números decimales4

PR O B L E M A S

1 ) En un supermercado venden bolsas con diferentesf r u t a s .La bolsa A dice: “peso 3,3 kilogramos”.La bolsa B dice: “peso 3,25 kilogramos”.Si quiero llevar la bolsa que contiene más fruta,¿cuál elijo?

COMPARACIÓN Y ORDEN DE NÚMEROS DECIMALES

PROBLEMAS

8) Para calcular.

b ) Basándote en lo resuelto en 8 a), calculá:

0,5 : 2 = 0,3 : 2 =

0,05 : 2 = 0,03 : 2 =

9) Resolvé los problemas.

a ) Si se colocan, una al lado de otra, 10 tiras de0,5 metros de longitud cada una, ¿qué largoforman en total? ¿Cuánto es 0,5 x 10 ?

b ) Si se colocan, una al lado de la otra, 10 tirasde 0,8 metros de longitud cada una, ¿quélargo forman en total? ¿Cuánto es 0,8 x 10 ?

c ) Si se colocan, una al lado de la otra, 10tiras de 0,04 metros de longitud cada una,

¿qué largo forman en tota l? ¿Cuánto es0,04 x 10 ?

d ) Si se colocan, una al lado de la otra, 10 tiras de0,84 metros de longitud cada una, ¿qué largoforman en total? ¿Cuánto es 0,84 x 10 ?

10) Más problemas para resolver.

a) Si se parte en 10 trozos igua les una t irade 0,5 metros de longitud, ¿cuánto midecada trozo? ¿Cuánto es 0,5 : 10 ?

b) Si se parte en 10 trozos igua les una t irade 0,04 metros de longitud, ¿cuánto m idecada trozo? ¿Cuánto es 0,04 : 10 ?

c) S i se parte en 10 trozos igua les una t irade 0,54 metros de longitud, ¿cuánto m idecada trozo? ¿Cuánto es 0,54 : 10 ?


0,4 : 2 =

2 ) Martina pesaba 55,5 kilogramos. Hoy se subió a labalanza y extrajo un t i c k e t que decía 55,500 kilo-gramos. Preocupadísima afirmaba que subió depeso. ¿Es cierto esto?

3 ) El chocolate “Qué rico” cuesta $ 2,05 y el chocola-te “Choco Choc”, $ 2,50. Los dos pesan lo mismo.¿Cuál es el chocolate más económico?

Matemátic a . Fracc iones y números dec ima les. 6º grado • Apuntes para la enseñanza 47

AN Á L I S I S D E L O S P R O B L E M A S 1, 2, 3, 4, 5, 6, 7, 8, 9 Y 10

El trabajo con comparación de números decimales comenzó en 5° grado, p o rtanto, es probable que muchos niños ya hayan incorporado como recurso parac o mpararlos el considerar primero el número que tenga mayor la parte entera, luegoel que tenga mayor la cifra que está en el lugar de los décimos, y por último la cifraque está en el lugar de los centésimos, etc. Sin embargo, es posible que aún haya quie-nes, a la hora de comparar, conciban los números decimales como pares de númerosnaturales separados por una coma: así consideran que 1,5 es menor que 1,50 porque5 es menor que 50. Es esa una oportunidad para repensar criterios que permitan re-chazar elaboraciones como las anteriores y enriquecer así las relaciones que subyacenen la escritura decimal.

4 ) Completá los espacios con el signo menor (<), ma-yor (>) o igual (=) según corresponda:

a ) 1 , 5 1 , 5 0

b ) 0 , 2 9 9 0 , 3

c) 0 , 0 4

d) 0 , 1

e ) 0 , 0 3

f ) 0 , 4 0

5 ) Ordenar de menor a mayor:7,4; 8,3; 7,12; 8,08; 7,04; 8,15; 8,009; 8,01 3

6 ) Resolvé los problemas:

a ) Matías y Elena jugaban a adivinar números.Mientras lo hicieron con números natura-les no hubo problemas, pero cuando juga-ron con números decimales se generó la si-guiente discusión.

MAT Í A S: “Adivina, adivinador... El número queyo pensé está entre 2,4 y 2,5”.

EL E N A: “Siempre el mismo tramposo, no exis-ten números entre 2,4 y 2,5”.

¿Quién pensás que tenía razón?

b ) Matías le dio a Elena varios ejemplos de nú-meros mayores que 2,4 y menores que 2,5.

¿ Podés vos pensar algunos?

c ) Elena, entusiasmada, ve que ahora sí le puedeganar a Matías.

EL E N A: “Adivina adivinador... Mi númeroestá entre 1,15 y 1,16, y t iene tres cifrasd e c i m a l e s ”.

¿Qué números habrá pensado Elena? Proponét r e s .

d ) En la última jugada Matías propone:

“ Pensé un número que está entre 5,62 y 5,63,y tiene dos lugares después de la coma”.

Elena sostiene que ganó esa mano ya que es-ta vez Matías sí se había equivocado.

¿Tiene razón Elena? ¿Por qué?

7 ) Escribí tres números entre

a) 1,5 y 1,6

b) 2,03 y 2,04

c) 5,17 y 5,2

d) 11,9 y 12

e) 0,2 y 0,21

8 ) Escribí tres números decimales menores que 0,01 .

9 ) Escribí una fracción entre los siguientes números:

a) 0,5 y 0,7

b ) 1,1 y 1,2

c) 12,05 y 12,06

10) Escribí un número decimal entre los siguientes nú-m e r o s :

y 1

y

y

34

110

12100

45

910

21010

1.0003

1004010


Nuevamente se realizarán análisis del tipo:

1,50 es equivalente a 1

1,5 es equivalente a 1

es equivalente a

Por tanto, ambas expresiones son equivalentes.

El problema 6 apunta a dos cuestiones: por un lado, a mostrar la densidad de losnúmeros racionales ya que efectivamente hay infinitos números entre 2,4 y 2,5, porejemplo, 2,48; 2,456; 2,4733... Pero, por otro lado, también es relevante mostrar la li-mitación al acotar la cantidad de cifras decimales.

En el caso de buscar números de 3 cifras decimales entre 1,15 y 1,16, el maestropodrá analizar en forma colectiva las respuestas preguntando cómo se puede estar se-guro de que no hay más que las que se mencionaron.

Otro aspecto interesante para tener en cuenta en el caso de los ejercicios en losque se propone intercalar números decimales es que, aprovechando la descontextua-lización, el maestro aliente las propuestas de escribir números con varias cifras des-pués de la coma puesto que esta posibilidad no es válida cuando nos manejamos concontextos como el del dinero o algunas unidades de medida.

La suma y resta de números decimales fue trabajada en 5° grado. Esta actividad pre-tende avanzar en esos contenidos.

PROBLEMAS

1 ) Lorena y Alejandra querían unir sus cintas por elborde. Lorena decía que uniendo su cinta de 1,5metros a la de Alejandra de 1,6 metros tendríanuna cinta de 2,11 metros. Alejandra pensaba quesi unían ambas cintas tendrían una cinta de másde 3 metros. ¿Quién estaba en lo cierto? ¿Cómopensó el cálculo cada una?

2) En la caja del supermercado te dicen que tenésque pagar $ 5,75. Si lo hacés con un billete de$10, ¿cómo hacés para calcular mentalmentelo que te deben dar de vuelto?

3) Si en el visor de la calculadora tenés el núme-ro 0,234, qué operación deberías hacer paraque aparezca...

0,134 0,235

0,244 0,24

1,234

OPERACIONES CON NÚMEROS DECIMALES. SUMA Y RESTA

4) Resolvé mentalmente

10 + 0,2 = 1 - 0,5 =

2 - 0,05 = 3 + 0,7 =

1 - 0,25 = 4 - 1,15 =

4 + 0,02 = 1 - 0,75 =

4 - 2,30 = 10 + 0,2 + 0,03 =

2 - 1,1 = 8,9 + 1,1 =

0,5 + 0,05 + 0,005 = 10 - 0,91 =

1,14 + 1,16 =

5) Sumá 0,9 a cada uno de los siguientes números:3,1; 3,11; 4,25; 0,73; 2,99.

Restá 0,9 a cada uno de los siguientes números:8,6; 3,4; 12,5; 8,25.

Operaciones con números decimales. Suma y resta5

50100

50100510510

Matemátic a . Fracc iones y números dec ima les. 6º grado • Apuntes para la enseñanza 49

AN Á L I S I S D E L O S P R O B L E M A S 1, 2, 3, 4, 5, 6, 7 Y 8

En el problema 1, una forma de justificar el resultado correcto sería expresando enfracciones los números en cuestión:

1,6 = 1 +

1,5 = 1 +

como + = y = 1,

es equivalente a 1 + . El resultado de la suma es entonces

1 + 1 + 1 + = 3 +

que es en lo que pensó Alejandra al afirmar que la suma era mayor que 3.

El trabajo con la calculadora vuelve a poner en juego el valor posicional en las es-crituras decimales. La calculadora funciona como herramienta de control de anticipa-ciones, que el docente debe indicar que se hagan por escrito.

Los problemas 5, 6 y 7 se relacionan entre sí. Mientras que el problema 5 propo-ne explorar una estrategia para sumar 9 décimos, centésimos o milésimos, el proble-ma 6 “invita” a explicitar la regla que se ha utilizado y que no necesariamente fueenunciada y analizada para resolver el ejercicio precedente. El problema 7 permite ex-tender el procedimiento utilizado (sumar el entero inmediatamente superior a los 9décimos, centésimos o milésimos y restar 0,1; 0,01 ó 0,001, según el caso) a otros nú-meros que no están compuestos sólo por 0 y 9, como 1,9; 2,99, etcétera.

Sumá 0,09 a cada uno de los siguientes núme-ros: 2,23; 1,75; 9,91; 3,55.

Restá 0,09 a cada uno de los siguientes núme -ros: 8,29; 12,71; 4,35; 8,28.

6) Algunas personas cuando tienen que sumar 0,9a un número decimal le suman 1 y luego lequitan 0,1. Por ejemplo, para hacer 3,4 + 0,9, lopiensan así: 3,4 + 1 = 4,4.Luego hacen 4,4 – 0,1 = 4,3. Entonces,3,4 + 0,9 = 4,3. Esta regla funciona. Teniendo encuenta los cálculos que realizaron en el ejercicioa n t e r i o r, ¿qué reglas escribirán para restar 0,9?¿Y para restar 0,09? ¿Y para sumar 0,09?

7) Calculá mentalmente:

35,15 + 0,19 =

2,134 + 0,199 =

8,34 – 1,9 =

15,60 + 1,99 =

9,53 – 2,9 =

7,931 + 2,99 =

8 ) Matías y Diego jugaban a “Quien no pasa la línea”.

Matías partía del 0 y siempre debía sumar unnúmero. Diego partía del 1 y siempre debía res-tar un número. Matías no podía llegar a un nú-mero mayor que el de Diego; de lo contrario,perdía. Diego no podía llegar a un número me-nor que el de Matías, pues, de lo contrario, per-día él.Estas son las primeras jugadas:

Matías Diego

0 1+ 0,1 = – 0,1 = + 0,1 = – 0,1 =+ 0,02 = – 0,1 =+ 0,005 = – 0,05 =+ 0,0005 = – 0,09 =

¿A qué número llegó cada uno de los partici-pantes?¿Puede Matías agregar 3 números más sin per-der? ¿Y Diego?

510

510

610

610

1010

1110

1110

110

110

110


Esta regla también podría extenderse a otros números, por ejemplo 0,8 (sumar unentero y restar 0,2). Se sugiere reflexionar con los alumnos, de ser posible, si utiliza-rían la misma estrategia para sumar números como 2,1; 3,2; 11 , 01; es decir, númerosque están a uno o dos décimos de un entero pero que se encuentran “más cerca” delentero anterior que del siguiente.

Posiblemente aquí convenga discutir que en estos casos se puede sumar pri-mero la parte entera y, al resultado obtenido, sumarle la parte decimal. Por ejemplo:7,34 + 3,1, se puede pensar como 7,34 + 3 = 10,34. Entonces 10,34 + 0,1 = 10,44. Esdecir, 7,34 + 3,1 = 10,44.

Los alumnos abordarán estas primeras situaciones en las que tienen que “sacar deci-males” en una división de números enteros, apoyados en sus conocimientos sobre me-didas. La idea es alentar diferentes resoluciones para, a partir de ellas, enseñar el pro-cedimiento de “bajar los ceros cuando la cuenta entera se acaba”.

AN Á L I S I S D E L O S P R O B L E M A S 1, 2 Y 3

Para comenzar a realizar la división involucrada en el problema 1, los alumnospodrán basarse en la transformación de los pesos en centavos pero orientándo-los a que el resultado lo consideren en pesos, de modo de recuperar así la expre-sión decimal.

$ 12 : 15$ 12 = 1.200 c1.200 c : 15 = 80 c ó $ 0,80.

Ahora bien: ¿cómo reconstruir la cuenta para que el resultado sea 0,80?El cambio de unidades proporciona “pistas” para entrar al algoritmo convencio-

nal. El docente podrá explicar que al pasar los pesos a centavos se multiplica por 10 0el dividendo y luego, para recuperar el resultado en pesos, se divide por 100.

De manera similar, para averiguar la distancia entre los carteles, podrían expresarlos kilómetros en metros, 18 kilómetros =18.000 metros.

Cociente decimal de dos números naturales. Expresion decimal de fracciones no decimales

6

PROBLEMAS

1 ) Un quiosquero compró una caja con 15 latas degaseosas a $12. ¿Cuánto pagó por cada una?

2 ) En una ruta que tiene 18 kilómetros quieren ubi-car 25 carteles publicitarios a igual distancia.¿Cada cuántos kilómetros deben colocarse?

3) ¿Es posible que pague una cuenta de $ 99 en 12cuotas de igua l va lor?

En caso de que sea posible , ¿cuá l sería esev a l o r ?

COCIENTE DECIMAL DE DOS NÚMEROS NATURALES. EXPRESIÓN DECIMAL DE FRACCIONES NO DECIMALES


18.000 : 25 = 720 metros720 metros = 0,72 km

Ahora bien, las unidades de longitud ofrecen la posibilidad de establecer un para-lelo entre las transformaciones de unidades y las transformaciones de los restos en elalgoritmo convencional, a fin de determinar el cociente decimal entre dos númerosnaturales. Ve a m o s :

18 kilómetros 250 kilómetros 7 hectómetros 2 decámetros

180 hectómetros 175 hectómetros 0, 72 km

5 hectómetros

50 decámetros

0 decámetros

La transformación de kilómetros en hectómetros y de hectómetros en decámetrospuede ponerse en paralelo con la transformación de enteros en décimos y de décimosen centésimos.

18 unidades 250 unidades 7 décimos de unidad 2 centésimos de unidad

180 décimos de unidad 175 décimos de unidad 0, 72

5 décimos de unidad

50 centésimos de unidad0 centésimos de unidad

El problema 3, si bien vuelve al contexto del dinero, marca una diferencia con elprimer problema ya que, al ser 99 mayor que 12, probablemente se comience la di-visión convencional y sea necesario pasar los pesos que sobran a centavos para seguirr e p a r t i e n d o .

$ 99 123 8 $

$ 3 = 30 décimos de peso 126 décimos de peso 2 décimos de peso

60 centésimos de peso 125 centésimos de peso

Por tanto, $ 99 : 12 = $ 8 + $ + $ ; o sea, $ 8,25.

Al finalizar esta actividad se espera que se hayan establecido relaciones que per-mitan arribar a las siguientes conclusiones:

• Para hallar los primeros cocientes decimales entre números naturales puedo,según el contexto, usar unidades menores que me permitan “repartir” y lue-go volver a expresar el resultado del reparto en la unidad original.

• Cuando en una división de naturales “sobra” un resto, lo puedo transformaren décimos y seguir dividiendo los décimos; si sobran décimos, los puedotransformar en centésimos y dividir los centésimos.

A partir de esta actividad se espera establecer la equivalencia que existe entre dividirpor 10, 100, 1.000 y multiplicar por 0,1; 0,01; 0,001 .

AN Á L I S I S D E L O S P R O B L E M A S 1, 2, 3, 4 Y 5

La estructura posicional de la notación decimal es el recurso que sirve para ex-plicar tanto las divisiones como las multiplicaciones por las potencias de 10.


¿Dividir por 10, 100, 1.000 o mult iplicar por 0,1, 0,01, 0,001 ?

7

PR O B L E M A S

1 ) Revisá las actividades en las que trabajamos conlongitudes para recordar cómo se multiplica unnúmero decimal por 10, 100, 1.000.

2 ) Intercambiá con tu compañero algunas multi-plicaciones de decimales por 10, 100, 1.000 (vosproponés multiplicaciones y él te las propone avos). Analicen juntos los resultados de las multi-plicaciones que propusieron y anoten una reglapara multiplicar decimales por 10, 100, 1.000.

3 ) Hagan lo mismo con divisiones por 10, 10 0 ,1 . 0 0 0 .

4 ) Ya vimos que

1 : 10 = 0,1y también sabemos que 1 x 0,1 = 0,1De manera análoga: 2 : 10 = 0,2y también sabemos que 2 x 0,1 = 0,23 : 10 = 0,33 x 0,1 = 0,3

52 : 10 = (50 + 2) : 10 = 50 : 10 + 2 : 10 =5 + 0,2 = 5,252 x 0,1 = 50 x 0,1 + 2 x 0,1 = 5 + 0,2 = 5,2

Pareciera que dividir por 10 es lo mismo que mul-tiplicar por 0,1. Explorá si esto es siempre cierto y,si te convencés, encontrá un modo de explicarle aun compañero por qué funciona esta regla.

5 ) De manera análoga a lo que analizamos en elpunto anterior, estudiaremos ahora la relaciónentre dividir por 100 y multiplicar por 0,01. Pa r aeso comenzá haciendo algunas multiplicacionespor 0,01 y dividiendo esos mismos números por100. Te ayudamos con algunas propuestas:1 : 100 = 0,01 1 x 0,01 = 0,015 : 100 = 0,05 5 x 0,01 = 0,0534 : 100 = 0,34 34 x 0,01 = 0,34

Seguí probando con números de tres, cuatro ymás cifras. Encontrá en el problema anterior unamanera de explicar esta regularidad.

¿DIVIDIR POR 10, 100, 1.000 O MULTIPLICAR POR 0,1; 0,01; 0,001?

5100

210

Matemá tic a . Fra cc iones y números dec ima les . 6º grado • Apuntes para la enseñanza 53

Efectivamente, los alumnos ya deberían saber a esta altura que al dividir un cierto nú-mero por 10, las unidades se transforman en décimos, las decenas en unidades, lascentenas en decenas, los décimos en centésimos, los centésimos en milésimos, etc. Di-vidir un número natural por 10, por ejemplo 23, se puede pensar como 23 veces 1: 10 ,lo cual da 23 veces 0,1, o sea, 23 x 0,1.

Por otra parte, se puede recuperar el resultado de multiplicar un número naturalpor 0,1 apelando a la suma iterada: cada 10 veces que se suma 0,1 se obtiene 1. Así,50 x 0,1 es sumar 5 veces 10 x 0,1, lo cual da como resultado 5.

Del mismo modo se puede establecer la equivalencia entre dividir por 100 y mul-tiplicar por 0,1.

Es importante que los alumnos lleguen a una formulación de estas leyes y no so-lamente que den la regla sin su fundamento. El sentido de la actividad es alimentaruna justificación para multiplicar números decimales.

Se trabajará la resolución de situaciones de multiplicación de números decimales enel contexto de la proporcionalidad directa. También, las estrategias que permitanavanzar en la comprensión de los algoritmos convencionales para multiplicar núme-ros decimales y, a su vez, aquellas estrategias que establezcan control sobre estos.

Al igual que el trabajo realizado con fracciones, la proporcionalidad directa seráel contexto en el cual los alumnos podrán apoyarse para conocer el resultado de mul-tiplicaciones y divisiones con números decimales, aun antes de conocer los procedi-mientos requeridos para obtenerlo.

AN Á L I S I S D E L O S P R O B L E M A S 1 Y 2

Consideremos la tabla que relaciona la cantidad de dinero recaudado en función de lacantidad de asistentes. Para averiguar la cantidad de dinero recaudado para 10 perso-nas, se puede hacer el doble de 7,75, que es 15,5. De ahí, puede obtenerse el valor dela entrada correspondiente a 1 persona, esto es 1,55.

PROBLEMAS

1) La siguiente tabla muestra el dinero que se re-cauda en una boletería en relación con la can-tidad de personas que asisten a un paseo:

2) La siguiente tabla vincula el precio que debepagarse por distintas cantidades de queso si seconoce el precio de 1 kilogramo.


Dinero recaudado ($)

5 10 1 2 12

12,407,75

Peso del queso( k i l o g r a m o s )

Precio ($)

1 0,5 0,25

13,2510,60

LA PROPORCIONALIDAD DIRECTA, LA MULTIPLICACIÓN Y LOS NÚMEROS DECIMALES

La proporcionalidad directa, la multiplicación y los números decimales

8


Para hallar la cantidad de personas con quienes se recauda $ 12,40 puedehaber de diversas formas. Una de ellas sería pensar en ir sumando 1,55 tantasvec es como se a ne cesario hasta l legar a $ 12,40, o sea , 8 veces. Otro modoes considerar que por 2 personas se re caudan $ 3,10 y que 4 veces $ 3,10 es$ 12,40.

Completada la tabla, se “tienen” los siguientes cálculos aunque estos no hayan si-do realizados vía una estrategia específica:

5 x 1,55 = 7,75

10 x 1,55 = 15,5

2 x 1,55 = 3,10

12 x 1,55 = 18,6

Ahora bien, cualquiera de estos cálculos puede pensarse si se pasan los pe-sos a centavos: se obtendría el total recaudado en centavos. Luego, para “tener-lo” en pesos, habría que dividir los centavos por 100. Esto puede ayudar a que losalumnos entiendan —por lo menos en este contexto— por qué las multiplicacio-nes anteriores se pueden pensar como multiplicaciones de números naturales, enlas que después “se corre la coma dos lugares”. Esta estrategia sirve para multi-plicar un número natural por un decimal y será reutilizada, aunque no exacta-mente de la misma manera, en el problema siguiente.

En el caso de la segunda tabla es posibl e averiguar el precio de 0,5 kg,puesto que es la mitad de $ 10,60, precio correspondiente a 1 kg, o sea, $ 5,30.El precio de kg puede averiguarse si se ca lcula la mitad del precio corres-pondiente a kg o la cuarta parte de lo que le corresponde a 1 kg, esto es,$ 2,65. Si fuera necesario el docente actual izará las relac iones:

0,5 = =

0,25 = =

1,25 = =

Probablemente para averiguar el valor de 1,25 kg sumen el va lor corres-pondiente a 1 kg más el va lor correspondiente a 0,25 kg, o sea, $13,25.

Por otra parte, la constante de proporc ionalidad de esta tabla es 10,60, quees el precio correspondiente a 1 kg de queso. Quedan entonces planteados enel pizarrón los siguientes cálculos con sus respectivas respuestas, cuyos resul-tados se han asegurado aun desconociendo el algoritmo convenc ional paramultipl icar decima les: con estos números la tabla “c i e r r a ”.

0,5 x 10,60 = 5,30

0,25 x 10,60 = 2,65

1,25 x 10,60 = 13,25

A partir de aquí el maestro deberá expl icar cómo tratar de reconstruir es-tos cá lculos. Una posibi lidad será proponer un cambio de unidades: 0,5 kg es

14

1454

12

12

51025100125100


lo mismo que 500 gramos. Si 1 kg cuesta $ 10, 60, 100 gramos cuestan $1,06;por tanto, 500 gramos cuestan 5 x 1,06 = 5,3.

Veamos en deta lle las transformaciones en juego:0,5 x 10,60 = 5 x 1,06. O sea, se mult iplicó un factor por 10 y el otro se divi-dió por 10 para “conservar” el resultado.

¿Func ionarán transformac iones parec idas a éstas para los otros cálculos?Ve a m o s :0,250 kg es lo mismo que 250 gramos; esto es, 100 gramos + 100 gramos + 50 gra-mos, lo cual indica que hay que multiplicar por 2,5 el precio de 100 gramos, que es$1,06. Aunque no se adelanta mucho porque se vuelve a obtener un cálculo con dosnúmeros decimales, sí se puede ver que 0,250 x 10,60 = 2,5 x 1,06. O sea nueva-mente se muestra que el producto no altera si se multiplica un factor por 10 y sedivide el otro por 10. Si ahora se repite la operación, aunque en el contexto no re-sulte fácil ver su sentido, queda:0,25 x 10,60 = 2,5 x 1,06 = 25 x 0,106 = 2,65

Lo que se recorta de este trabajo es la posibilidad de transformar los cálculosen otros equivalentes, de modo tal que uno de los factores sea un número natural.

De alguna manera, la coma de uno de los factores “se carga” al otro factor.

Ensayemos las transformaciones con la tercera cuenta en cuestión:1,25 x 10,60 = 125 x 0,1060 = 13,25

Veamos otra manera de pensar las transformaciones. Retomemos el cálculo: 0,5 x 10,60 se puede pensar 0,5 como 5 x 0,1; y 10,6 como 106 x 0,1 (es-to ha sido analizado en la actividad anterior). Resulta entonces que 0,5 x 10,6 = 5 x 0,1 x 106 x 0,1 ó 5 x 106 x 0,1 x 0,1= 5 x 106 x 0,01

Esta expresión “muestra” más claramente por qué se multiplican los números “c o-mo si fueran naturales” y luego se “corre la coma”.

PROBLEMA

3 ) Indicá si es verdadera o fa lsa cada una de lassiguientes af irmac iones. Expl icá cómo lop e n s a s t e .

a) Cuando se multiplica un número decimalpor un número natural, el producto siem-pre es mayor que el número natural.

b) Cuando se multiplica un número decimal porun número natural, el producto siempre esmayor o igual que el número decimal.

c) El producto de dos números decimales siem-pre tiene tantas cifras decimales como lasuma de las cifras decimales de ambos nú-meros.

d) El producto de dos números decimales nun-ca puede ser un número natural.

LA PROPORCIONALIDAD DIRECTA, LA MULTIPLICACIÓN Y LOS NÚMEROS DECIMALES



Los alumnos podrán retomar los cálculos de la actividad anterior como una fuente deexploraciones frente a estas preguntas “más teóricas”:

1,55 x 5 = 7,75

1,55 x 2 = 3,10

1,55 x 12 = 18,60

0,5 x 10,60 = 5,30

0,25 x 10,60 = 2,65

1,25 x 10,60 = 13,25

Esta discusión puede reeditar aquella anterior (planteada ya en 5° grado)acerca de productos que son menores que uno de los factores. Se sugiere pro-fundizar esto solicitando a los alumnos que especifiquen en qué casos:

• un producto de dos factores es mayor que cada uno de los factores;• un producto de dos factores es menor que uno de los factores y mayor que

el o t r o ;• un producto de dos factores es menor que los dos factores.

Será también ésta una oportunidad para discutir el lugar de la coma (cantidad decifras decimales) del producto de dos números decimales.

La tradición escolar enseña tempranamente que el producto de dos números de-cimales tiene tantas cifras decimales como la suma de las cifras decimales de ambosfactores. Entendemos que no es conveniente dar esta idea sin que los alumnos hayantenido previamente la posibilidad de encontrar estrategias personales y elementos pa-ra fundamentar los procedimientos convencionales.

Fracciones y decimales 6 docente

Education

Transcript of Fracciones y decimales 6 docente