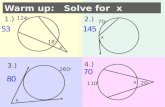
Warm Up Solve for x. 1. x 2 + 38 = 3 x 2 – 12 2. 137 + x = 180 3. 4. Find FE .
EXAMPLE 1 Solve by equating exponents Rewrite 4 and as powers with base 2. 1 2 Solve 4 = x 1 2 x –...
-
Upload
erik-marsh -
Category
Documents
-
view
214 -
download
0
Transcript of EXAMPLE 1 Solve by equating exponents Rewrite 4 and as powers with base 2. 1 2 Solve 4 = x 1 2 x –...

EXAMPLE 1 Solve by equating exponents
Rewrite 4 and as powers with base 2.
12
Solve 4 = x 1
2
x – 3
(2 ) = (2 )2 x – 3x – 1
2 = 2 2 x – x + 3
2x = – x + 3
x = 1
SOLUTION
4 =x 1
2
x – 3
Write original equation.
Power of a power property
Property of equality for exponential equations
Solve for x.
The solution is 1.ANSWER

EXAMPLE 1 Solve by equating exponents
Check: Check the solution by substituting it into the original equation.
Substitute 1 for x.
Simplify.
Solution checks.
4 =?12
– 2
1 – 3
4 =1 ? 12
4 = 4

GUIDED PRACTICE for Example 1
Solve the equation.
1. 9 = 27 2x x – 1
9 = 27 2x x – 1
SOLUTION
(3 ) = (3 )2 x – 12x 3
3 = 3 4x 3x – 3
Rewrite 9and 27 as powers with base 3.
Write original equation.
Power of a power property
4x = 3x –3 Property of equality for exponential equations
9 = 27 2x
9 = (9•3) 2x x – 1

GUIDED PRACTICE for Example 1
4x – 3x = –3
= –3 Solve for x.
Property of equality for exponential equations
The solution is – 3.ANSWER

GUIDED PRACTICE for Example 1
Solve the equation.
2. 100 = 1000
7x + 1 3x – 2
SOLUTION
(10 ) = (10 )2 3x – 27x+1 3 Rewrite 100and 1000 as powers with base 10.
Write original equation.
Power of a power property
14x + 2 = 9x – 6 Property of equality for exponential equations
100 = 1000 7x + 1 3x – 2
(10 ) = (10 )9x – 614x+2

GUIDED PRACTICE for Example 1
14x – 9x = – 6 – 2
Solve for x.
Property of equality for exponential equations
5x = – 8 Property of equality for exponential equations
– 8 5
The solution is .ANSWER
x = – 8 5

GUIDED PRACTICE for Example 1
Solve the equation.
81 = 3 – x 1
3
5x – 6
3 = 3 12 – 4x – 5x+6
Rewrite 81 and 1/3 as powers with base 3.
Write original equation.
Power of a power property
12 – 4x = – 5x+6 Property of equality for exponential equations
(3 ) = (3 )
3 – x4 – 1 5x – 6
SOLUTION
3. 81 = 3 – x 13
5x – 6

GUIDED PRACTICE for Example 1
– 4x + 5x = 6 – 12 Property of equality for exponential equations
x = – 6 Solve for x.
The solution is – 6 .ANSWER