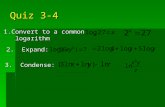
Evaluate the following: Recall: a logarithm is an exponent. So in each case, we are looking for the...
-
Upload
katherine-dixon -
Category
Documents
-
view
212 -
download
0
Transcript of Evaluate the following: Recall: a logarithm is an exponent. So in each case, we are looking for the...

WHAT ARE THE PROPERTIES OF LOGARITHMS?

Evaluate the following:
4
64log
64log
16log
4log
2log
2
2
2
2
2
Recall: a logarithm is an exponent. So in each case, we are looking for the exponent of 2 to get a number. In the first example, the answer is 1
1
Because 221 246
4

4
64log
64log
16log
4log
2log
2
2
2
2
2 1
246
4
Compare example 4 with examples 2 and 3What do you notice?
If we multiply 4 and 16 we’ll get 64
If we add 2 and 4 we get 6
There is a relationship between these examples.
16log4log64log 222

Another way of seeing this:
164log64log 22
16log4log164log 222
But we know that
416log
24log
2
2
So we can
substitute to get:
42So we found that:
6164log64log 22 We should check our answer:
664log2 6426 This is true, so our answer is correct.

In the same manner, we can create rules for the logarithm of a quotient and the logarithm of something raised to a powerIf we do that, we have the following properties of logarithms1) The product rule:
caca bbb logloglog 2) The quotient rule:
cac
abbb logloglog
3) The power rule:
aca bc
b loglog

Example – Use the laws of logarithms to expand the logarithm
32log yxbThere are two laws we can apply here: the power and the product rule. We must do the product rule first.
32 loglog yx bb Now we can apply the power rule:
yx bb log3log2

Example – Use the laws of logarithms to expand the logarithm
y
xblog
Quotient rule first
yx bb loglog We can apply the power rule also, if we change the form of the square root of x
yx bb loglog 2
1
yx bb loglog2
1

Example – Use the laws of logarithms to write the following expression as a single logarithm
yx log3log2 Before we use quotient rule, we must use the power rule32 loglog yx Now the quotient rule
3
2
logy
x

Example – Use the laws of logarithms to write the following expression as a single logarithm
znm loglog3log2
1
znm logloglog 32
1
znm logloglog 3 zmn loglog 3
z
mn3log