Diplomarbeit - theorie.physnet.uni-hamburg.de · Er unterscheidet sich von einem Molekül vor allem...

I. Institut fürTheoretische Physik

Variational Cluster Approximation mit stochastischem Cluster-Solver

Variational Cluster Approximation with a stochastic cluster solver

28.01.2009

1. Gutachter: Prof. Dr. M. Potthoff2. Gutachter: Prof. Dr. A. Lichtenstein

Diplomarbeit

vorgelegt von Sebastian Bäse

Universität HamburgDepartment Physik

KurzzusammenfassungIn dieser Arbeit wird die erstmalige Verwendung einer stochastischen Methode für die Varia-tional Cluster Approximation (VCA), einer Quanten-Cluster-Methode zur Untersuchung starkkorrelierter Elektronensysteme, diskutiert.In der VCA wird die Komplexität des Gittermodells auf die eines Systems von entkoppel-ten Clustern reduziert. Bislang wurden für die VCA lediglich die Exakte Diagonalisierungund die Lanczos-Methode als Cluster-Solver benutzt. Diese Lösungsmethoden weisen jedocheinen exponentiell ansteigenden Rechenaufwand mit wachsender Clustergröße auf und sind des-halb auf kleine Cluster beschränkt. Für große Cluster bieten sich stochastische Methoden an,wie zum Beispiel die Quanten-Monte-Carlo-Techniken, deren Rechenaufwand in Abwesenheitdes Vorzeichenproblems lediglich in einem Potenzgesetz skaliert. Monte-Carlo-Algorithmen ha-ben wiederum die Schwäche, dass sie nicht das für die VCA benötigte großkanonische Po-tential des Clusters liefern. Daher wird in dieser Arbeit ein alternativer stochastischer An-satz als VCA-Cluster-Solver vorgestellt, der auf einer diagrammatischen Quanten-Monte-Carlo-Methode (weak-coupling Continous Time Quantum Monte Carlo; wcCT-QMC) basiert. Derneue Algorithmus, der eine Version des Wang-Landau-Algorithmus darstellt und daher alswcCT-WL bezeichnet wird, liefert nicht nur neben der Matsubara-Funktion das großkanoni-sche Potential des Clusters, sondern kann im Rahmen des Hubbard-Modells ohne größerenMehraufwand numerisch exakte Ergebnisse kontinuierlich in der Wechselwirkunsstärke erzeu-gen.Als Anwendungsbeispiel der Kombination von VCA und wcCT-WL wurde der Crossover vomMetall zum Isolator oberhalb der kritischen Temperatur des Mott-Übergangs des zweidimensio-nalen Hubbard-Modells untersucht. Dabei lieferte die neue Methode vergleichbare Ergebnissewie andere Cluster-Methoden mit Quanten-Monte-Carlo-Solvern. Deshalb gelang es nun mitdem neuen Cluster-Solver die VCA auf wesentlich größere Cluster bei endlichen Temperaturenzu erweitern.

AbstractThis thesis presents the first application of a stochastic method for the Variational Cluster Ap-proximation (VCA) - a quantum cluster approach to strongly correlated electrons. So far, onlyExact Diagonalization and the Lanczos method have been used to solve the cluster problem ofthe VCA. These methods show an exponential increase of the computing time for an increasingcluster size. For large clusters stochastic methods, e.g. Quantum Monte Carlo techniques, arevery powerful and widely used, because in absence of the sign problem their computing timescales in a power law. A disadvantage of the Monte Carlo algorithms is that they do not providethe cluster grand potential which is used in the VCA. So an alternative stochastic approachbased on a diagrammatic Quantum Monte Carlo method (weak coupling Continous Time Quan-tum Monte Carlo; wcCT-QMC) will be presented. The new algorithm is a version of the wellknown Wang-Landau algorithm. Therefore the algorithm will be denoted as wcCT-WL. Thereis an interesting advantage of this cluster solver: It provides not only the Matsubara function,the expectation value of observables and the grand potential but also all results as a continousfunction of the interaction strength.The study of the high temperature crossover from a metal to an insulator in the two dimensionalHubbard model was used to test the combination of VCA and wcCT-WL. The new techniqueshows results comparable to other cluster methods with a Quantum Monte Carlo solver.

DanksagungAn dieser Stelle möchte ich die Gelegenheit wahrnehmen, einigen Personen zu danken.

Mein besonderer Dank gilt Herrn Prof. Dr. Michael Pothoff für die sehr gute Betreuung meinerDiplomarbeit. Seine wertvollen Hinweise und Anregungen haben dazu beigetragen, dass meineArbeit in der vorliegenden Form entstehen konnte.

Ferner bedanke ich mich bei Aschraf Charafeddine und Matthias Balzer für die Dialoge überdie Variational Cluster Approximation und über den Mott-Übergang, die nicht unwesentlich zumeinem Verständnis dieser Themen beigetragen haben.

Letzlich möchte ich meiner ganzen Familie danken, die mich immer wieder neu motivierenkonnte, als es zu Problemen bei der Implementierung der Kombination von der VariationalCluster Approximation mit dem stochastischem Cluster-Solver kam. Dabei möchte ich meineFreundin Sina Brandt hervorheben und mich für ihre Unterstützung sowie die sehr hilfreichenDiskussionen über die Mathematik der Markov-Ketten-Monte-Carlo-Methoden bedanken.

Inhaltsverzeichnis

1 Einleitung 1

2 Theoretische Grundlagen 52.1 Das Großkanonische Potential Ω . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52.2 Das Hubbard-Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.2.1 Der Hubbard-Hamiltonian . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72.3 Die Matsubara-Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102.4 Die Selbstenergie und die Dyson-Gleichung . . . . . . . . . . . . . . . . . . . . . . 172.5 Das Wick-Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

3 Variational Cluster Approximation 213.1 Das Luttinger-Ward-Funktional Φ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223.2 Die Selbstenergiefunktionaltheorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243.3 Cluster-Approximationen innerhalb der SFT . . . . . . . . . . . . . . . . . . . . . 253.4 Numerische Auswertung des SFT-Funktionals . . . . . . . . . . . . . . . . . . . . 283.5 Auswertung der Stationaritätsbedingung . . . . . . . . . . . . . . . . . . . . . . . . 313.6 Clustergeometrien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 333.7 Optimierung des Intraclusterhoppings . . . . . . . . . . . . . . . . . . . . . . . . . 343.8 Badplätze als zusätzliche Freiheitsgrade . . . . . . . . . . . . . . . . . . . . . . . . 35

4 Der stochastische Cluster-Solver 374.1 Grundlagen der Markov-Ketten-Monte-Carlo-Methoden . . . . . . . . . . . . . . 37

4.1.1 Markov-Ketten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 384.1.2 Ergodizität und stationäre Verteilung von Markov-Ketten . . . . . . . . . 394.1.3 Metropolis-Algorithmus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 414.1.4 Thermalisierung und Autokorrelation . . . . . . . . . . . . . . . . . . . . . 44

4.2 Weak-coupling CT-QMC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 494.2.1 Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 494.2.2 Detaillierte Beschreibung für das Hubbard-Modell . . . . . . . . . . . . . 574.2.3 Update-Formeln und Messung von Erwartungswerten . . . . . . . . . . . 62

4.3 Der Wang-Landau-Algorithmus als VCA-Cluster-Solver . . . . . . . . . . . . . . . 64

5 Der Mott-Übergang und der Hochtemperatur-Crossover im 2D-Hubbard-Modell 755.1 Grundlagen des Mott-Übergangs . . . . . . . . . . . . . . . . . . . . . . . . . . . . 755.2 Der Mott-Übergang am Temperaturnullpunkt . . . . . . . . . . . . . . . . . . . . 765.3 Der Mott-Übergang bei endlichen Temperaturen . . . . . . . . . . . . . . . . . . . 785.4 Die stochastisch ausgewertete VCA und der Hochtemperatur-Crossover . . . . . 80

6 Fazit und Ausblick 89

I

Inhaltsverzeichnis

A Berechnung der Spektralmomente 91

B Beweise 93B.1 Beweis von Formel (2.1.5) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93B.2 Beweis von Formel (4.2.11) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93B.3 Beweis von Formel (4.2.12) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94B.4 Fouriertransformation von (4.2.34) . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

C Schätzung von Fittingparametern 97

II

1 Einleitung

Zahlreiche Anwendungen im heutigen Leben, sei es in der Unterhaltungselektronik, in derComputer- oder Medizintechnik, basieren auf den Erkenntnissen aus dem Studium der Ei-genschaften fester Materialien. Insbesondere sind die Struktur, die elektronischen und die ther-mischen Eigenschaften fester Körper von großem Interesse. Dabei besteht ein Festkörper wiejede Art kondensierter Materie aus Atomen, die durch chemische Bindungen zusammengehal-ten werden. Er unterscheidet sich von einem Molekül vor allem dadurch, dass die Anzahl derbeteiligten Atome so groß ist, dass der Festkörper in seiner Gesamtheit ein makroskopischesObjekt ist. Typischerweise sind ungefähr 1023 Atome pro Kubikzentimeter in einem Festkörperenthalten, wodurch die Anwendung einer quantentheoretischen Statistischen Physik sinnvollerscheint. Ein solches quantenmechanisches System von einer Vielzahl wechselwirkender Teil-chen ist im Allgemeinen so komplex, dass es nicht analytisch exakt lösbar ist. Das Zurückführenkomplexer Erscheinungen auf einige wenige, fundamentale Gesetzmäßigkeiten ist nur durch Mo-dellbildung möglich. Daher hat die Festkörpertheorie die Beschreibung von Festkörpern durcheine geeignete Modellbildung als Ziel, wodurch das Studium der Eigenschaften dieser Modelleund der Vergleich der Resultate mit der Realität im Vordergrund steht. Ein gutes Modell ist sokomplex, dass es die interessanten Aspekte der Natur einfängt, aber andererseits auch hinrei-chend einfach, um es noch lösen zu können. Bis auf wenige Spezialfälle lassen sich selbst zumTeil stark vereinfachte Modelle nicht exakt lösen, so dass man stets gezwungen ist, weitere Nä-herungen durchzuführen. Dabei muss natürlich darauf geachtet werden, dass die physikalischenVoraussetzungen des zu erklärenden Phänomens bewahrt bleiben. Auch wenn es möglich ist eineTheorie zu konstruieren, die exakt alle messbaren Eigenschaften der Festkörper voraussagt, sindabstraktere Modelle notwendig, um die verschiedenen Eigenschaften und verschiedenen physi-kalischen Systeme zu klassifizieren, damit die für spezielle Effekte entscheidenden Bestandteileidentifiziert werden können. So werden oft für eine sinnvolle Beschreibung der verschiedenenEigenschaften eines Materials jeweils spezielle unterschiedliche Modelle entwickelt. Für eine rea-listischere Beschreibung kann man eine Hierachie von immer komplexeren Theorien aufbauen,so dass der Gültigkeitsbereich ausgeweitet wird und die Genauigkeit so verbessert wird, dassdie Ergebnisse mit denen aus Experimenten übereinstimmen.

Für einen einfachen Kristall kann angenommen werden, dass die aus einem positiv gelade-nen Kern und der ihn umgebenden negativ geladenen Elektronenhülle bestehenden Atome eineregelmäßige, mehr oder weniger starre Anordnung bilden, so dass die Geometrie des Festkörpersdurch ein periodisches Gitter modelliert werden kann. Weiterhin ist wegen der starken Coulomb-Wechselwirkung ein Großteil der Elektronen eng in den atomähnlichen Schalen der Ionen ge-bunden. Die resultierenden Atomrümpfe liefern dann ein periodisches Hintergrundpotential undschirmen die Wechselwirkung zwischen den restlichen Elektronen ab. Diese Valenzelektronenbestimmen in erster Linie die elektronischen, magnetischen und thermischen Eigenschaften derFestkörper. Somit genügt es die Modellierung auf die Valenzelektronen zu beschränken, umInformationen über solche Eigenschaften herauszufinden.

Die Überlappung der atomaren Orbitale benachbarter Gitterplätze führt nach Bloch [8] zurBildung von Energiebändern, die den Valenzelektronen eine Bewegung über den gesamten Fest-

1

1 Einleitung

körper erlauben. So kann man in einem einfachen Modell den grundlegenden Mechanismus fürLeitungseigenschaften metallischer Festkörper verstehen.Wegen dem Pauli-Ausschließungsprinzip kann jeder Eigenzustand nur von einem Elektron be-setzt werden. Eine Folge davon ist, dass triviale Korrelationen zwischen den Elektronen auchin einem wechselwirkungsfreien System existieren. Die Bewegung der Elektronen unter diesenBedingungen hängt offensichtlich stark von der Gitterstruktur ab.Die gitterabhängige Energie der nicht-wechselwirkenden Elektronen wird dabei üblicherweiseals kinetische Energie bezeichnet.Neben dem Potential des Gitters und der Pauli-Abstoßung unterliegen die Elektronen des Wei-teren der gegenseitigen Abstoßung durch die Coulomb-Wechselwirkung. Wenn die Überlappungder Orbitale groß ist, wird deren Einfluss nur gering sein, da die Elektronen einander bequemausweichen können. Ist hingegen die Überlappung gering, kommt es zur Ausbildung sehr schma-ler Bänder, in denen die gegenseitige Behinderung der Elektronenbewegung für die physikali-schen Eigenschaften sehr wichtig wird. Somit bewirkt auch die potentielle Energie, die mitder abgeschirmten Elektron-Elektron-Coulomb-Wechselwirkung assoziiert wird, Korrelationenzwischen den Valenzelektronen. Diese Korrelationen führen im Allgemeinen zu ganz überra-schenden, häufig spektakulären und bislang noch ungeklärten Phänomenen, wie unter anderemzu der Hochtemperatur-Supraleitung [9], dem itineranten Magnetismus oder dem MottschenMetall-Isolator-Übergang [76]. Dabei kommen diese Phänomene nur unter bestimmten äußerenBedingungen zum Vorschein, da stark korrelierte Elektronensysteme extrem empfindlich aufkleine Änderungen von Parametern wie der Temperatur, dem Druck oder Dotierung reagieren.So interessant diese Systeme für mögliche Anwendungen sind, wie magnetische Speicherelemen-te oder supraleitende Magneten in Kernspintomographen, so problematisch ist aber auch ihreModellierung, da die Bedeutung der Korrelationen zwar erkannt wurde, aber ihre mathemati-sche Handhabung sehr schwierig ist.Ausgangspunkt der Modellierung ist dabei die Idee des Gitters, in der die elektronischen Wel-lenfunktion im Ortsraum dargestellt werden. Diese so genannten Wannier-Funktionen sind anden Gitterplätzen lokalisiert und laufen so aus, dass sie jeweils einen Überlapp zu den Nachbar-plätzen herstellen. Man beschreibt somit effektiv Elektronen, die auf den Gitterplätzen sitzenund zwischen diesen hin- und herhüpfen können. Um schmale Bänder zu realisieren, kann voneinem geringen Überlapp der Wellenfunktionen und somit von einer starken Abschirmung aufdem Gitter ausgegangen werden. Damit ist auch eine Beschränkung auf Wechselwirkungenzwischen Elektronen, die sich auf demselben Platz befinden (Onsite-Wechselwirkung), gerecht-fertigt. Diese Gedanken führen auf das Hubbard-Modell [10], das eine adäquate Beschreibungfür stark korrelierte Elektronensysteme liefert.

Um die niederenergetischen elektronischen Eigenschaften einiger Materialien zu verstehen, mussdie Elektron-Elektron-Wechselwirkung nicht unbedingt explizit mitberücksichtigt werden. Fürgute Metalle ist dies durch die phänomenologische Landau-Theorie [20] gerechfertigt, die dieElektronen durch nicht-wechselwirkende Quasiteilchen mit einer renormierten Masse und einerendlichen Lebensdauer ersetzt. Wenn das wechselwirkungsfreie Bild versagt, können manchePhänomene wie langreichweitige Ordnung innerhalb einer statischen Molekularfeldtheorie [65]beschrieben werden. Hier wird der Effekt der Elektron-Elektron-Wechselwirkung auf jedes Elek-tron durch eine zeitgemittelte elektronische Ladungsdichte ersetzt. Im Allgemeinen, aber ins-besondere bei den stark korrelierten Elektronensystemen, versagt dieses effektive Ein-Teilchen-Bild, um die physikalischen Phänomene von Interesse zu reproduzieren, da hier der Einflusseines Elektrons auf ein anderes einfach zu ausgeprägt ist, um diese unabhängig voneinander zubehandeln. Bei diesen Systemen muss die volle Dynamik des elektronischen Korrelationspro-blems bewahrt werden.

2

Die Dynamische Molekularfeldtheorie (DMFT; [66]) liefert eine solche nicht-perturbative Appro-ximation für Modelle stark korrelierter Elektronen, im Speziellen für Varianten des Hubbard-Modells, welche im Limes unendlich großer Koordinationszahlen des Gitters exakt wird, dasheißt, dass jeder Gitterplatz unendlich viele Nachbarplätze besitzt. Die Approximation ver-nachlässigt die kurzreichweitigen räumlichen Korrelationen zwischen den Elektronen, währendihre dynamischen Korrelationen für die Beschreibung vieler interessanter Phänomene von kor-relierten Elektronensystemen entscheidend sind. Die DMFT vereinfacht das Gitterproblem aufein Störstellenmodell eingebettet in ein selbstkonsistent zu bestimmendes als Bad bezeichne-tes Medium. Dazu werden numerisch exakte Lösungsmethoden, so genannte Solver, verwendet.Eine wichtige Klasse dieser Solver nehmen die Quanten-Monte-Carlo-Methoden [42] ein, dietrotz des mit der Gitterplatzzahl exponentiellen Wachstums vom Hilbert-Raum eine in einemPotenzgesetz wachsende Rechenzeit aufweisen, sofern nicht das so genannte Vorzeichenproblemauftritt.

Auch wenn die DMFT die Konkurrenz zwischen kinetischer Energie und lokaler Coulomb-Abstoßung und somit die wesentliche Physik stark korrelierter Elektronensysteme erfasst, istdie Näherung durch Vernachlässigung der Effekte nicht-lokaler Fluktuationen zur Beschreibungder Physik von Spinwellen, der Lokalisierung in ungeordneten Systemen oder von Spinflüssig-keiten unzureichend. Es werden also nicht-lokale Korrekturen zur DMFT benötigt, um solcheSysteme oder Phasenübergänge, die durch nicht-lokale Ordnungsparameter beschrieben werden,zu behandeln. In den letzten Jahren wurden Varianten der DMFT ([69],[70]) entwickelt, die dasGitterproblem nicht auf eine Störstelle abbilden, sondern auf ein Teilsystem, ein so genanntesCluster, dessen Plätze in ein effektives selbstkonsitent zu bestimmendes Medium eingebettetsind. Neben diesen Molekularfeldtheorien für Cluster gab es mit der Variational Cluster Ap-proximation (VCA; [25]) eine auf einem Variationsprinzip beruhende alternative Entwicklungeiner Cluster-Methode, die in dieser Arbeit ausführlich erläutert werden soll. Bislang wurden fürdie VCA lediglich die Exakte Diagonalisierung und die Lanczos-Methode als Cluster-Solver be-nutzt. Diese Lösungsmethoden weisen jedoch einen exponentiell ansteigenden Rechenaufwandmit wachsender Clustergröße auf und sind deshalb auf kleine Cluster beschränkt. Für großeCluster bieten sich stochastische Methoden an, wie zum Beispiel die Quanten-Monte-Carlo-Techniken. Monte-Carlo-Algorithmen haben wiederum die Schwäche, dass sie nicht das für dieVCA benötigte großkanonische Potential des Clusters liefern.Ziel dieser Arbeit ist es einen alternativen stochastischen Ansatz als VCA-Cluster-Solver vorzu-stellen und die ersten Ergebnisse der Kombination von VCA und diesem für den Crossover vomMetall zum Isolator [87] oberhalb der kritischen Temperatur des Mott-Übergangs des zweidi-mensionalen Hubbard-Modells zu diskutieren.

3

2 Theoretische Grundlagen

In diesem Kapitel sollen grundlegende theoretische Überglegungen, die für das Verständnisder folgenden Kapitel benötigt werden, zusammengefasst dargelegt werden. Dies beinhaltetinsbesondere das Hubbard-Modell für stark korrelierte Elektronensysteme, sowie das Konzeptder Matsubara-Funktion und der Selbstenergie, aus denen sich wesentliche Informationen undEigenschaften über das System ableiten lassen. Außerdem wird das großkanonische Potentialeingeführt, das der Selbsenergiefunktionaltheorie als grundlegende thermodynamische Größedient, und das Wick-Theorem vorgestellt.

2.1 Das Großkanonische Potential Ω

In dieser Arbeit sollen physikalische Systeme betrachtet werden, die sowohl thermischen alsauch Teilchenaustauschkontakt mit der Umgebung aufweisen. Die Gesamtheit solcher Systeme,die das jeweils betrachtete System in einem bestimmten Zustand repräsentieren, wird als groß-kanonisches Ensemble bezeichnet.Durch thermischen Kontakt mit einem Wärmebad wird die inverse Temperatur β des betrachte-ten Systems mit Hamiltonian H fest vorgegeben, während die Energie des Systems fluktuierenkann. Außerdem sorgt der Teilchenaustauschkontakt mit einem Teilchenreservoir für ein be-stimmtes chemisches Potential µ, wohingegen die Teilchenzahl N veränderlich ist. Dabei spieltdie Umgebung in den folgenden Betrachtung keine Rolle [1].Die Bedeutung, die die Entropie S im mikrokanonischen Ensemble besitzt und die freie Ener-gie F im kanonischen Ensemble, übernimmt im großkanonischen Ensemble das großkanonischePotential Ω.Das großkanonische Potential kann über die großkanonische Zustandssumme Ξ definiert werden:

Ω = −1β

lnΞ . (2.1.1)

Dabei ist die großkanonische Zustandssumme Ξ gegeben durch

Ξ = tr e−βH−µN= tr e−βH, (2.1.2)

wobei H =H−µN als großkanonischer Hamiltonian angesehen werden kann. Die Zustandssum-me Ξ kann als Wahrscheinilchkeitsnormierung des großkanonischen Dichteoperators ρ = e−βH~Ξverstanden werden, das heißt also, dass durch die Spurbildung die unnormierten Gewichte al-ler dem betrachteten quantenmechanischen System zugänglichen reinen Zustände aufsummiertwerden. Durch diese statistische Betrachtung lassen sich quantenmechanische Erwartungswerteeiner Observablen A schreiben als:

`Ae = trρA = 1Ξ

tr e−βHA . (2.1.3)

Dass die Definition (2.1.1) über die Zustandssumme mit dem ersten Hauptsatz der Thermo-dynamik konsistent ist, kann leicht nachvollzogen werden, wenn die Entropie S als partielle

5


Ableitung des großkanonischen Potentials Ω nach der Temperatur T bzw. als partielle Ablei-tung nach der inversen Temperatur β = 1~T aufgefasst wird, also gilt:

Ω = `He − TS = −1β

lnΞ .

Wie man sich leicht überzeugen kann, lässt sich nicht nur die Entropie S, sondern auch diemittelere Teilchenzahl `Ne durch eine partielle Ableitung des großkanonischen Potentials Ωdarstellen:

`Ne = 1Ξ

trN e−βH−µN=

1Ξ

1β

tr∂

∂µe−βH−µN

=∂

∂µ− 1

βln tr e−βH−µN = −∂Ω

∂µ. (2.1.4)

Dies ist nicht der einzige Erwartungswert, der sich aus einer Ableitung des großkanonischenPotentials ergibt. Allgemein lässt sich der Erwartungswert eines linear angekoppelten OperatorsA im Hamiltonian der Form H =H ′ + λA durch partielles Ableiten nach λ ermitteln, also

`Ae λ′ = ∂Ω∂λVλ=λ′

. (2.1.5)

Der Beweis dazu ist dem Anhang B.1 zu entnehmen. Man beachte, dass dies ein weiteres Konzeptzur Bestimmung von Erwartungswerten liefert. So kann der physikalische Hamiltonian lediglichfür einen bestimmten Wert für λ realisiert sein, sodass die partielle Ableitung (2.1.5) an derStelle λ = λphys für den gesuchten Erwartungswert betrachtet werden muss.Anzumerken sei noch, dass bei allen Prozessen, die bei konstanter inverser Temperatur β undkonstantem chemischen Potential µ möglich sind, nimmt das großkanonische Potential nicht zu,d.h.

dΩ B 0, (2.1.6)

und es ist demzufolge minimal im Gleichgewicht. Von dieser wichtigen Eigenschaft soll nochspäter im Zusammenhang mit der Selbstenergiefunktionaltheorie im Abschnitt 3.2 Gebrauchgemacht werden.

6

2.2 Das Hubbard-Modell

2.2 Das Hubbard-ModellDas Hubbard-Modell wurde erstmals 1963 unabhängig voneinander von J. Hubbard [10], vonJ. Kanamori [11] und von M.C. Gutzwiller [12] zur Beschreibung stark korrelierter Elektronenvorgeschlagen. J. Hubbard hat 1963 und in den Folgejahren eine Vielzahl von Arbeiten zu die-sem Modell veröffentlicht, so dass das Modell heute seinen Namen trägt.Das Hubbard-Modell wurde ursprünglich zur Beschreibung der Elektronen aus den schmalen3d-Bändern von Übergangsmetallen (Eisen, Kobalt, Nickel), die Ferromagnetismus aufweisen,eingeführt. Es zeigte sich schnell, dass es verschiedene Phänomene stark korrelierter Elektro-nensystem sehr gut modelliert, so zum Beispiel den Mottschen Metall-Isolator-Übergang [78].Neben dem Ferromagnetismus [15] zeigt das Hubbard-Modell auch Antiferro- [17], Ferri- [16]und Paramagnetismus [18]. Seit der Entdeckung der Hochtemperatursupraleiter wird es in ver-schiedenen Varianten zur Erklärung der Eigenschaften dieser Materialien herangezogen. Dabeiweist das Hubbard-Modell eine d-Wellen-Supraleitung auf [13].Inzwischen hat sich somit das Hubbard-Modell als Standard-Modell zur Beschreibung vondem nicht-trivialen Zusammenspiel von kinetischer Energie, Coulomb-Wechselwirkung, Pauli-Prinzip und Gitterstruktur stark korrelierter Elektronensystemen etabliert.

2.2.1 Der Hubbard-HamiltonianDie exakte Beschreibung von Viel-Teilchen-Systemen erfordert die Lösung von entsprechendenViel-Teilchen-Schrödinger-Gleichungen. Dies ist allerdings in der Regel unmöglich. Zur Vereinfa-chung der Bechreibung wird oftmals die so genannte zweite Quantisierung benutzt, die allerdingsnur eine Umformulierung des Viel-Teilchen-Problems darstellt. Dazu werden Konstruktionsope-ratoren c† und c eingeführt, die das mühsame Konstruieren der Viel-Teilchen-Wellenfunktionenals symmetrisierte bzw. antisymmetrisierte Produkte von Ein-Teilchen-Wellenfunktionen er-sparen. Die für die Teilchen zugrunde liegende Statistik wird dabei durch die fundamentalenVertauschungsrelationen der Konstruktionsoperatoren ausgedrückt. Für ein Viel-Elektronen-System gilt die Fermi-Statistik, die durch die folgenden Antikommutatorregeln der fermioni-schen Konstruktionsoperatoren zum Ausdruck gebracht wird:

ci, c†j = δij , ci, cj = c†

i , c†j = 0. (2.2.1)

Im Folgenden sollen nun die Valenzelektronen eines Festkörpers als Viel-Elektronen-System be-trachtet werden. Diese stammen aus nicht abgeschlossenen Schalen der Festkörperatome undtragen daher zur Festkörperbindung bei. Damit sind sie auch für typische Festkörpereigenschaf-ten verantwortlich. Im Gegensatz dazu sind die restlichen Festkörperelektronen, die Rumpf-elektronen, in unmittelbarer Nähe der Atomkerne lokalisiert, sodass sie zusammen mit demjeweiligen Kern zu einem Gitterion zusammengefasst werden können. Diese Gitterionen bildenin einem idealen Festkörperkristall eine periodische Struktur, die als Gitter bezeichnet wird.Daher verursachen diese Ionen ein Potential für die Valenzelektronen, das die Gitterperiodi-zität wiederspiegelt. Dementsprechend lassen sich Gittermodelle für Festkörper konstruieren.Hierbei wird das Gittermodell durch einen Hamiltonian charakterisiert, der bezüglich einerEin-Teilchen-Orthonormalbasis formuliert ist, deren Elemente durch einen Gitterplatzindex i,den orbitalen Freiheitsgrad m am Platz i und durch den Spinfreiheitsgrad σ indiziert werden.Diese Freiheitsgrade sollen von nun an zu einem Index zusammengefasst werden:

α = i,m,σ.Daher werden auch die Erzeugungs- bzw. Vernichtungsoperatoren entsprechend indiziert:

c†α bzw. cα .

7


Damit ergibt sich für den Hamiltonian wechselwirkender Elektronen im Festkörper allgemeinsterForm in zweiter Quantisierung:

H =Qαβ

tαβ c†αcβ +

12Q

αβγδ

Uαβδγ c†αc†

βcγcδ. (2.2.2)

Der erste Term beschreibt das Hopping nicht-wechselwirkender Elektronen auf dem Gitteraufgrund der Überlappung der Orbitale benachbarter Atome. Der zweite Term spiegelt dieZwei-Teilchen-Wechselwirkung der Elektronen untereinander wieder. Dabei sind die Hopping-Matrixelemente tαβ und die Wechselwirkungsmatrixelemente Uαβδγ bestimmt durch:

Uαβδγ = `αβSVee Sδγe (2.2.3)tαβ = `αS − p2~2m + Vion Sβe , (2.2.4)

wobei p der Impuls eines Valenzelektrons, Vion das Gitterpotential und Vee die Elektron-Elektron-Coulomb-Wechselwirkung ist.Wird nun angenommen, dass die langreichweitigen Anteile der Coulomb-Wechselwirkung zwi-schen den Valenzelektronen abgeschirmt werden, dominieren die Beiträge der Onsite-Matrixele-mente des Wechselwirkungsterms. Diese Annahme führt zu einer drastischen Vereinfachung desModells, indem die Elektron-Elektron-Wechselwirkung nur berücksichtigt wird, wenn sich zweiElektronen auf dem selben Gitterplatz befinden. Weiterhin sei aufgrund des geringen Über-lapps der Orbitale auch nur ein Hüpfen zwischen benachbarten Plätzen zugelassen. Um dasModell möglichst einfach zu halten, wird zudem die Bandentartunug vernachlässigt, d.h. manbeschränkt sich auf nur ein Orbital pro Gitterplatz. Zwei Elektronen, die sich am selben Git-terplatz befinden und damit miteinander wechselwirken, haben dann wegen des Pauli-Prinzipsnotwendigerweise entgegengesetzten Spin. Unter diesen Annahmen folgt zusammen mit derTatsache, dass die Matrizen t = tij und U = Uijlk wegen der Spinunabhängkeit des Git-terpotentials bzw. wegen der Spinunabhängigkeit der Elektron-Elektron-Wechselwirkung auchspinunabhängig sind:

Uαβδγ = Uδαβδαγδαδ und tαβ = tij =

¢¦¤t, wenn i nächster Nachbar von j,

0, sonst, (2.2.5)

und der Hamiltonian (2.2.2) vereinfacht sich zu dem Ein-Band-Hubbard-Modell:

H = t Q`i,je,σ

c†iσcjσ − ε0Q

iσ

niσ

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶=H0

+UQi

nini

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶=H1

. (2.2.6)

Hier parameterisieren t die kinetische Energie und U die Coulomb-Wechselwirkung. Des Weite-ren beschränken die Klammern `i, je die Summation auf Nächstnachbarpaare von den Gitter-plätzen i und j. Der Operator niσ = c†

iσciσ misst die Besetzung vom Platz i durch ein Elektronmit Spin σ. Folglich ist nini der Doppelbesetzungsoperator. Abbildung 2.1 stellt die konkur-rierenden Beiträge bezogen auf ein Gitter dar.Wird ein unendlich ausgedehntes Gitter betrachtet, um die makroskopische Größe eines Festkör-pers zu modellieren, so ergibt sich für das Hubbard-Modell eine Translationsinvarianz. Damitlässt sich durch die Fourier-Transformation

ckσ =1ºLQj

e−iRjkcjσ cjσ =1ºL

1.BZ

Qk

eiRjkckσ, (2.2.7)

8

2.2 Das Hubbard-Modell

Abbildung 2.1: Schematische Darstellung des Hubbard-Modells: Bei Doppelbesetzung eines Platzes findet dieWechselwirkung U zwischen den beiden Elektronen statt. Das Hüpfen eines Elektrons zwischenzwei benachbarten Plätzen wird durch t parameterisiert.

wobei L die Anzahl der Gitterplätze ist und die k-Summation sich nur über die erste Brillouin-Zone erstreckt, der Ein-Teilchen-Anteil des Hamiltonians H0 diagonalisieren. Da der freie AnteilH0 nicht mit dem Wechselwirkungsterm H1 kommutiert, führt die Fouriertransformation nichtzur Diagonalisierung des gesamten Hamiltonians, dessen Eigenzustände somit Linearkombina-tionen aus den Eigenzuständen der beiden Anteile sind. Damit ist die Lösung des Hubbard-Modells alles andere als trivial und nur in wenigen Grenzfällen (z.B. Fermi-Gas-Limes U 0,atomarer Limes N = 1) analytisch exakt lösbar. Eine spezielle Rolle spielt das eindimensionaleHubbard-Modell. Es ist eine so genannte Luttinger-Flüssigkeit. Das eindimensionale Hubbard-Modell ist damit in vieler Hinsicht verschieden von dem Verhalten in höheren Dimensionen.Mit Hilfe des Bethe-Ansatzes konnten E.H. Lieb und F.Y. Wu [14] die Grundzustandsenergieexakt berechnen. Eine allgemeine analytisch exakte Lösung für das Hubbard-Modell in höhe-ren Dimension wurde bislang nicht gefunden. Angesichts der Komplexität des Problems undder hohen Genauigkeit numerischer Methoden besteht auch kein Interesse in der analytischenBehandlung des Hubbard-Modells in höheren Dimensionen.Durch Ausnutzung von Symmetrien des Hubbard-Modells, die im Wesentlichen die dem Gitterzugrunde liegenden Symmetrien und die Invarianz gegenüber Spinrotationen sind, lässt sich dieBeschreibung vereinfachen. Dabei ist die Invarianz unter Teilchen-Loch-Transformationen eineweitere und oft sehr hilfreiche Symmetrie. Die grundlegende Transformation ist dabei

T1 c†iσ ciσ, ciσ c†

iσ,

die alle Elektronen in Löcher und alle Löcher in Elektronen transformiert. Des Weiteren be-trachte man die Transformation

T2 c†iσ −1ic†

iσ, ciσ −1iciσ.

Diese Transformation bewirkt einen Wechsel des Vorzeichens der kinetischen Energie. Für dasHubbard-Modell mit Nächstnachbarhopping ist der Hamiltonian unter dieser Transformationinvariant und das Vorzeichen der Hoppingamplitude t kann frei gewählt werden. Bei Hinterein-anderausführung dieser beiden Transformationen wird der großkanonische Hamiltonian folgen-dermaßen verändert:

H − µN H +UL −N − 2µL2L −N. (2.2.8)

9


Folglich bleibt bei einem halbgefüllten System der Hamiltonian invariant unter der Transfor-mation T2 X T1. Damit hat man also eine weitere Symmetrie. Insbesondere lässt sich mit Hilfedieser Transformationen herleiten, für welches chemische Potential µ Halbfüllung des Systems(N = L) vorliegt. Dazu betrachte man die erwartete Besetzung des Systems:

`Ne µ,β =1Ξ

1β

∂

∂µtr exp−βH − µN

T2XT1=

1Ξ

1β

∂

∂µtr exp−βH +UL −N − µ2L −N

= 2L −1Ξ

trN exp−βH + U − 2µL − U − µN

Offensichtlich liegt für alle inversen Temperaturen β halbe Bandfüllung nur vor, wenn daschemische Potential µ = U~2 beträgt.

2.3 Die Matsubara-FunktionIn diesem Abschnitt wird das Konzept der Matsubara-Funktion, die auch oft als Temperatur-Green-Funktion oder als Propagator bezeichnet wird, vorgestellt, da diese Größe eine funda-mentale Rolle in der diagrammatischen Behandlung von Vielteilchensystemen bei endlichenTemperaturen spielt. Die Matsubara-Funktion ist allerdings nicht von direktem Interesse undist eher als Hilfsgröße zu verstehen, aus der sich zum Beispiel die Spektraldichte und alle ther-modynamischen Erwartungswerte berechnen lassen.

Bei Betrachtung einer zeitabhängigen Korrelationsfunktion

ÀtB0e 7= À0Bt + iβe (2.3.1)

wird offensichtlich, dass es sinnvoll ist, den Definitionsbereich der Zeiten im Heisenberg-Bildauf die komplexe Ebene zu erweitern. Damit lassen sich die Zeiten darstellen durch t = θ − iτ .Der Vorteil der imaginären Zeiten liegt in der Störungsentwicklung begründet: Jede „konventio-nelle“ Störungstheorie basiert auf der Annahme, dass sich der Hamiltonian H des betrachtetenSystems gemäß H = H0 +H1 in einen exakt lösbaren Anteil H0 und in eine Störung H1 zerle-gen lässt. Bei endlichen Temperaturen besteht nun das Problem, dass für die Berechnung desErwartungswertes einer Observablen A, also

Àe = trAHt e−βH

tr e−βH, (2.3.2)

formal sowohl eine Entwicklung für den zeitabhängigen Operator AHt = eiHtAS e−iHt imHeisenberg-Bild1 als auch eine für den Dichteoperator ρ = e−βH durchgeführt werden muss.Wird nun jedoch β als Real- oder Imaginärteil einer komplexen Zeit aufgefasst, lassen sich dieExponentialfunktionen zusammenfassen.Insbesondere gelingt es durch einen Übergang zu rein imaginären Zeiten τ = it, der als Wick-Rotation bezeichnet wird, eine Entwicklung von zeitabhängigen Korrelationsfunktionen in Po-tenzen des Wechselwirkungsterms des Hamiltonians diagrammatisch darzustellen, was im All-gemeinen für rein reelle Zeitabhängigkeiten nicht möglich ist.Durch die Wick-Rotation wurde somit ein modifiziertes Heisenberg-Bild mit Operator AHτ =1AS ist hierbei der entsprechende Operator im Schrödinger-Bild ohne explizite Zeitabhängigkeit.

10

2.3 Die Matsubara-Funktion

eHτAS e−Hτ und ein modifiziertes Dirac-Bild mit Operator ADτ = eH0τAS e−H0τ geschaffen.Man beachte, dass der für die imaginäre Zeitverschiebungen verantwortliche Operator eHτ nichtunitär ist.Eine Verknüpfung der beiden Bilder wird nun durch den Diracschen Zeitentwicklungsoperator2

Sτ, τ ′ = eH0τ e−Hτ−τ′ e−H0τ ′ mit 0 B τ, τ ′ B β (2.3.3)

hergestellt, wobei β die inverse Temperatur bezeichnet. Mit dem Diracschen Zeitentwicklungs-operator S lässt sich also der Operator im modifizierten Heisenberg-Bild durch den entspre-chenden im modifierzierten Dirac-Bild ausdrücken:

AHτ = S0, τADτ Sτ,0 . (2.3.4)

Es lässt sich außerdem zeigen, dass mit dem Zeitordnungsoperator T sich der Diracsche Zeit-entwicklungsoperator durch

Sτ, τ ′ = T exp−Sτ

τ ′dτ ′′H1τ ′′

darstellen lässt [2]. Daraus folgend ergibt sich der Zusammenhang

e−βH= Sβ,0 e−βH0 (2.3.5)

zwischen dem Dichteoperator des wechselwirkenden Systems H und dem Dichteoperator desentsprechenden freien Systems H0. Damit besteht aber auch ein Zusammenhang zwischen dergroßkanonischen Zustandssumme Ξ des wechselwirkenden Systems und der Zustandssumme Ξ0

des freien Systems:

Ξ = tr e−βH= trSβ,0 e−βH0

= tr e−βH0trSβ,0 e−βH0

tr e−βH0= Ξ0 `Sβ,0e0 . (2.3.6)

Nach diesen Vorbereitungen wird nun mit der Ein-Teilchen-Matsubara-Funktion eine der zen-tralen Größen der Viel-Teilchen-Theorie eingeführt. Sie ist definiert durch

Gαβτ = − ` T cατc†β0 e (2.3.7)

mit den Vernichtungs- und Erzeugungsoperatoren im modifizierten Dirac-Bild, also cατ =eH0τ cαe−H0τ und c†

βτ ′ analog.Die Wahl der Zeitabhängigkeit der Operatoren wurde dahingehend gewählt, dass erkennbarwird, dass die Matsubara-Funktion lediglich von der Zeitdifferenz der Operatoren abhängt.Eine weitere Eigenschaft der Matsubara-Funktion ist ihre postulierte 2β-Periodizität. So giltfür fermionische Systeme:

Gαβτ + kβ = −Gαβτ + k − 1β für β A τ + kβ A 0, k > Z . (2.3.8)

Dadurch ist eine Betrachtung der Matsubara-Funktion lediglich auf dem Intervall 0, β völligausreichend.Aus der Definition der Matsubara-Funktion folgt mit den Gleichungen (2.3.5) und (2.3.6) fürdie Matsubara-Funktion:

Gαβτ = −Ξ−1 trT cατc†β0 Sβ,0 e−βH0

= −Ξ0

Ξ` T cατc†

β0 Sβ,0 e0 . (2.3.9)

2Der Diracsche Zeitentwicklungsoperator Sτ, τ ′ wird auch oft als S-Matrix bezeichnet.

11


Für die explizite Rechnung ist die Zeitdarstellung der Matsubara-Funktion oft ungünstig. Daherwird meist die Frequenzdarstellung benutzt, die durch die Fouriertransformation:

Gαβiωn = Sβ

0dτ Gαβτ eiωnτ

Gαβτ = 1β

ª

Qn=−ª

Gαβiωn e−iωnτ (2.3.10)

gewonnen wird.Dabei sind die Matsubara-Frequenzen für Fermionen3 definiert durch:

ωn = 2n + 1πβ

mit n > Z . (2.3.11)

Aus der Definition (2.3.7) der Matsubara-Funktion soll nun mit Hilfe der Bewegungsgleichungs-methode eine Darstellung der freien Matsubara-Funktion für ein nicht-wechsel-wirkendes Sys-tem mit dem großkanonischen Ein-Teilchen-Hamiltonian H0 = Pαβ tαβ − µδαβc†

αcβ gefundenwerden. Mit Hilfe der Definition

G0αβiωn = `` cα, c†

β ee0ωn(2.3.12)

lauten die Bewegungsgleichungen:

iωn`` cα, c†β ee0ωn

= `` cα, c†β ee0ωn

+ `` cα,H0 , c†β ee0ωn

= δαβ +Qβ′

tαβ′`` cβ′ , c†β ee0ωn

.

Die Kette der Bewegungsgleichungen bricht also ab und es tritt wegen des fehlenden Wechsel-wirkungsterms keine höhere Matsubara-Funktion auf. In der Matrix-Notation bedeutet dies:

iωnG0 = 1 + t G0 .

Damit ergibt sich für die freie Matsubara-Funktion

G0iωn = iωn + µ1 − t−1 . (2.3.13)

Nun ist im Allgemeinen die Matrix t nicht diagonal in der Orthonormalbasis Sαe. Damit istdie freie Matsubara-Funktion auch nicht diagonal. Da der Hamiltonian H0 hermitesch ist, istauch t hermitesch und es existiert eine unitäre Transformation U , die t diagonalisiert. DieDiagonalmatrix zu t sei im Folgenden ε. Die unitäre Transformation U wird aber auch die freieMatsubara-Funktion G0 diagonlisieren:

iωn + µ1 − ε−1 = iωn + µ1 −U †tU−1 = U † iωn + µ1 − tU−1

= U−1 iωn + µ1 − t−1 U †−1 = U † iωn + µ1 − t−1 U

= U †G0U = G0 .

Im Falle der Translationsinvarianz des Hamiltonians stellt die die Fouriertransformation diegesuchte unitäre Transformation dar, die t und G0iωn diagonalisiert. Im Allgemeinen müssendiese unitäre Transformationen aus der Lösung des dazugehörigen Eigenwertproblems beschafftwerden. Dabei sind die Eigenvektoren von t als Spalten der Transformationsmatrix U aufzu-fassen.Die Diagonalelemente der diagonlisierten Matrix G0iωn sind dann

G0miωn = iωn + µ − εm−1 , (2.3.14)

3Für bosonische Systeme sind die Matsubara-Frequenzen durch ωn = 2nπ~β mit n > Z definiert.

12


wobei εm die Diagonalelemente der Matrix ε sind. Die Diagonalisierung ist also auf die Bestim-mung der Eigenwerte der Hoppingmatrix t reduziert worden.Die Zeitdarstellung der freien Matsubara-Funktion ergibt sich entweder durch Fouriertransfor-mation oder direkt aus der Definition:

G0mτ = −`T cmτc†

m0e0= Θτ`cmτc†

m0e0 +Θ−τ`c†m0cmτe0

= −e−εm−µτ Θτ`cmc†me0 −Θ−τ`c†

mcme0= −e−εm−µτ Θτ1 − `nme0 −Θ−τ`nme0 .

Die erwartete Besetzung eines freien Systems ist gegeben durch die Fermi-Funktion

fω = 1eβω+ 1

(2.3.15)

und somit folgt also

G0mτ = −e−εm−µτ Θτ 1 − fεm − µ −Θ−τ fεm − µ (2.3.16)

Mitunter ist es wünschenswert die Matsubara-Funktion nicht in ihrer Diagonalbasis, sondernin ihrer ursprüngliches Basis zu erhalten. Dazu wird lediglich die Rücktransformation

G0τ = UGτU †

durchgeführt.

An dieser Stelle sollen noch weitere Eigenschaften der Matsubara-Funktion aufgezählt wer-den:Dazu betrachte man die so genannte Spektraldarstellung der Matsubara-Funktion

Gαβiωn = Sª

ª

Aαβωiωn − ω

dω . (2.3.17)

Durch diese lässt sich der Bezug zum Experiment herstellen. Dabei kann die fouriertransfor-mierte Spektraldichte Akω als die Linienform eines Photoemissionsexperimentes angesehenwerden. Sie gibt also die Wahrscheinlichkeitsamplitude an, mit der ein Teilchen mit Impuls kbei der Frequenz ω angetroffen wird.

• Aus der Spektraldarstellung folgt eine für Frequenzsummationen der Matsubara-Funktionnützliche Eigenschaft. Es gilt:

Gαβ−iωn = Sª

−ª

Aαβω−iωn − ω

dω = Sª

−ª

Aαβωiωn − ω

dω

= Gαβiωn. (2.3.18)

Dieses Verhalten des Imaginärteils der Matsubara-Funktion wird in Abbildung 2.2 veran-schaulicht.Insbesondere gilt bei Teilchen-Loch-Symmetrie:

Aαβω = Aαβ−ω Ô Re Gαβiωn = 0 (2.3.19)Ô Gαβ−iωn = −Im Gαβiωn = −Gαβiωn (2.3.20)

13


Abbildung 2.2: Imaginärteil der lokalen freien Matsubara-Funktion in der Frequenzdarstellung eines Zwei-Platz-Hubbard-Modells bei Teilchen-Loch-Symmetrie und inverser Temperatur β = 50.

Ist nun die Hoppingmatrix t symmetrisch, so ist die freie Matsubara-Funktion G0iωnsymmetrisch und die wechselwirkende Matsubara-Funktion Giωn im Falle einer lokalenWechselwirkung dann ebenfalls. Somit folgt mit der Eigenschaft (2.3.18) auch:

Gαβ−iωn = Gβα−iωn = Gβαiωn,was in der Matrixnotation gleichbedeutend ist mit

G−iωn =Giωn† . (2.3.21)

• Für große Frequenzen lässt sich die Matsubra-Funktion entwickeln:

Gαβiωn = Sª

−ª

dω′Sαβω′iωn − ω′

=1

iωnSª

−ª

dω′ Sαβω′ 11 − ω′

iωn

ωnQ1=

1iωnSª

−ª

dω′ Sαβω′ª

Qk=0

ω′

iωn

k

=

ª

Qk=0

1iωnk+1 S

ª

−ª

dω′ Sαβω′ ω′k

Mit der Definition des k-ten Moments der Spektraldichte (bzw. des Spektralmoments k-terOrdnung)

Mkαβ = S

ª

−ª

dω′ Sαβω′ ω′k = ` Lkcα, c†β e, (2.3.22)

wobei der Operator Lk das k-fache Bilden des Kommutators mit dem Hamiltonian meint:LA = A,H, ergibt sich als Hochfrequenzentwicklung der Matsubara-Funktion:

Giωn =ª

Qk=0

M k

iωnk+1 . (2.3.23)

14


Da insbesondere das nullte Spektralmoment gleich der Einheitsmatrix ist, also M 0= 1,

verschwindet der Imaginärteil der lokalen Matsubara-Funktion wie −1~ωn für sehr großeFrequenzen (Abbildung 2.3) unabhängig von der Wechselwirkung:

Im Gαβiωn ωnªÐ −

δαβ

ωn. (2.3.24)

Eine vergleichbare universelle Hochfrequenzabschätzung ist für den Realteil der Matsubara-

Abbildung 2.3: Konvergenzverhalten des Imaginärteils der lokalen freien Matsubara-Funktion G0iiiωn eines

Zwei-Platz-Hubbard-Modells bei Teilchen-Loch-Symmetrie und inverser Temperatur β = 50:Für große Frequenzen konvergiert ωn ċ Im G0

iiiωn gegen −1 und somit verschwindet dannIm G0

iiiωn wie −1~ωn.

Funktion nicht möglich, da bei der Berechnung des Spektralmoment erster Ordnung derKommutator mit dem Hamiltonian gebildet werden muss (siehe Anhang A).

• In der Zeitdarstellung ist die lokale Matsubara-Funktion Gαα unstetig bei τ = 0 [7]:

Gαβτ = 0+ = ` c†βcα e − δαβ

Gαβτ = 0− = ` c†βcα e

Gαβτ = 0+ − Gαβτ = 0− = −δαβ

Insbesondere ergibt sich also aus der lokalen Matsubara-Funktion bei der Zeit τ = 0− dieerwartete Besetzung vom Zustand Sαe:

Gαατ = 0− = `nαe . (2.3.25)

• Eine weitere Eigenschaft der Matsubara-Funktion in der Zeitdarstellung ist ihre Symme-

15


trie um τ = β~2, wenn Teilchen-Loch-Symmetrie vorliegt:

Gαβτ = β~2 + x = 1β

ª

Qn=−ª

Gαβiωn exp −iωnβ~2 + x

=1β

ª

Qn=0

Gαβ−iωn´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶=−Gαβiωn

exp iωnβ~2 + x

+

1β

ª

Qn=0

Gαβiωn exp −iωnβ~2 + x

= −

2i

β

ª

Qn=0

Gαβiωn sin2n + 1πβ

β

2+ ωnx

= −

2i

β

ª

Qn=0

Gαβiωn −1n cos ωnx´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶=cos−ωnx

= Gαβτ = β~2 − x . (2.3.26)

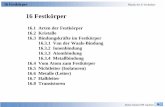
Abbildung 2.4: Lokale freie Matsubara-Funktion G0iiτ eines Zwei-Platz-Hubbard-Modells bei Teilchen-Loch-

Symmetrie und inverser Temperatur β = 10: Deutlich erkennbar íst die vorliegende Antisym-metrie bzgl. τ = 0 und die Symmetrie bzgl. τ = β~2.

16

2.4 Die Selbstenergie und die Dyson-Gleichung

2.4 Die Selbstenergie und die Dyson-GleichungEine zum vorherigen Abschnitt analoge Herleitung einer Darstellung für die Matsubara-Funktioneines wechselwirkendes Systems mittels Bewegungsgleichungen zeigt, dass der Wechselwirkungs-term im Hamiltonian im Allgemeinen dazu führt, dass die Kette der Bewegungsgleichungennicht mehr abbricht. Für die Ein-Teilchen-Matsubara-Funktion kann dieses Problem auf die sogenannte Selbstenergie Σ verschoben werden. Es ergibt sich für die Matsubara-Funktion

Giωn = iωn + µ1 − t −Σiωn−1 . (2.4.1)

Durch Vergleich mit der Darstellung (2.3.13) für die freie Matsubara-Funktion G0 stellt sichheraus, dass die Selbstenergie für ein nicht-wechselwirkendes System verschwindet, also ist Σ =0. Durch Einsetzen von (2.3.13) erhält man aus Gleichung (2.4.1):

Giωn = G−10 iωn −Σiωn−1 . (2.4.2)

Die Selbstenergie beschreibt demnach sämtliche Wechselwirkungseffekte. Die volle Bedeutungder Selbstenergie zeigt sich aber erst im Zusammenhang mit der diagrammatischen Störungs-theorie, in der sie definiert wird. Dazu betrachte man die Herleitung von (2.4.2).Ausgangspunkt ist dabei die Diagrammentwicklung der Matsubara-Funktion, die gegeben istdurch:

Die hier auftretenden Diagramme lassen sich in unterschiedliche Klassen einteilen. So werden dieTeile eines Diagramms mit Anschlussmöglichkeiten für je eine einlaufende und eine auslaufendeLinie als Selbstenergieeinschübe bezeichnet, zum Beispiel:

Daraus folgt auch schon die Definition der Selbstenergie. Diese ist die Summe der Beiträge vonirreduziblen Selbstenergieeinschüben, die also nicht durch Auftrennen eines Propagators in zweiTeile zerlegt werden können und wird durch

als Diagramm dargestellt. Alle reduziblen Diagramme lassen sich nun zusammenfassen undsich durch die Selbstenergie darstellen. So erhält man für die Diagramme, bei denen nur einPropagator aufgetrennt werden kann:

Nach Zusammenfassen aller reduziblen Diagramme ergibt sich die folgende Diagrammentwick-lung für die Matsubara-Funktion:

Ausklammern des ersten Selbstenergieterms zeigt, dass die verbleibende Summe in der Klammerwiederum die volle Matsubara-Funktion ergibt:

17


Dadurch erhält man letztlich für die Diagrammentwicklung der Matsubara-Funktion:

bzw. in der Matrix-Notation:G =G0 +G0 Σ G . (2.4.3)

Dies ist die so genannte Dyson-Gleichung, aus der sich Gleichung (2.4.2) durch Umformungergibt.Hat man einen approximativen Ausdruck für die Selbstenergie gefunden, so kann die Matsubara-Funktion durch Lösen der Dyson-Gleichung bestimmt werden. Dies kann aufgrund der oft ein-facheren Struktur der Selbstenergiediagramme von Vorteil sein.Außerdem liefert die Dyson-Gleichung eine alternative Darstellung der Selbstenergie:

Σ =G−10 −G−1. (2.4.4)

Hier wird wieder sichtbar, dass die Selbstenergie die Wechselwirkung des Systems wiederspie-gelt und für ein wechselwirkungsfreies System verschwindet.Die Dyson-Gleichung bietet vor allem eine Möglichkeit eine Approximation durch Aufsum-mieren von unendlichen Teilreihen zu entwickeln. Dies ist vorteilhaft, wenn die Störung nichtwirklich „klein“ ist oder wenn Divergenzen in den einzelnen Störtermen auftreten und somitbereits das Aufsummieren von endlich vielen Termen der Störreihe nicht mehr sinnvoll wird.Dieses Konzept soll nun anhand der Diagrammentwicklung der Selbstenergie verdeutlicht wer-den.Dabei werden Partialsummen von Diagrammen gebildet, die durch Hinzufügen von Selbstener-gieeinschüben in den Propagatoren des Ausgangsdiagramms entstehen. Zum Beispiel:

Diese Partialsummen werden durch Diagramme gekennzeichnet, die ausschließlich aus wechsel-wirkenden Propagatoren aufgebaut sind und keine Selbstenergieeinschübe enthalten. Sie werdendaher auch als angezogende Skelette bezeichnet. Damit erhält man die Selbstenergie als Summealler angezogenen Skelette:

Allerdings ist der wechselwirkende Propagator nicht bekannt und muss erst aus der Dyson-Gleichung bestimmt werden. Dies führt zu einem iterativen Verfahren, das bei Selbstkonsistenzabgebrochen wird und daher als selbstkonsistente Renormierung bezeichnet wird.

18

2.5 Das Wick-Theorem

2.5 Das Wick-TheoremDas Wick-Theorem stellt ein bedeutendes Hilfsmittel zur Auswertung eines freien Erwartungs-wertes eines zeitgeordneten Produkts der Konstruktionsoperatoren A,B,C, ... im Dirac-Bilddar, wie er zum Beispiel bei der großkanonischen Zustandssumme in (2.3.6) auftritt.Zunächst wird eine so genannte Kontraktion zweier Konstruktionsoperatoren A und B im mo-difizierten Dirac-Bild definiert durch:

AB = `TABe0 ,was im Wesentlichen in der diagammatischen Störungstheorie eine freie Ein-Teilchen-Matsubara-Funktion darstellt.Das Wick-Theorem besagt nun, dass der freie Erwartungswert vom zeitgeordneten Produkt derKonstruktionsoperatoren A,B,C, ... in die Summe aller möglichen Kontraktionen der Operato-ren zerfällt:

`TABC . . . XY Ze0 = ABC . . . XY Z + ABC . . . XY Z + ... (2.5.1)

Diese Aufteilung erfordert natürlich eine gerade Anzahl an Konstruktionsoperatoren. Dies istimmer gegeben, wenn die Teilchenzahl eine Erhaltungsgröße darstellt. Dann enthält der Erwar-tungswert `T ABC...XY Ze0 die gleiche Anzahl von Erzeugern und Vernichtern; also insgesamteine gerade Anzahl von Operatoren. Es verbleibt noch anzumerken, dass die zu kontrahieren-den Operatoren in benachbarte Positionen zu bringen sind, was für fermionische Operatorenfür jede notwendige Vertauschung einen Faktor −1 liefert.Das Wick-Theorem soll hier nicht weiter bewiesen werden. Daher sei an dieser Stelle auf diedetaillierte Diskussion in der Standardliteratur der Vielteilchentheorie verwiesen, z.B. [2],[4]oder [5].

19


20

3 Variational Cluster Approximation

Die Möglichkeit wechselwirkende Vielteilchensystemen, wie z.B. stark korrelierte Elektronen-systemen, numerisch exakt zu diagonalisieren oder mit der Lanczos-Methode zu lösen, wirdbeschränkt durch den mit der Systemgröße N exponentiell wachsenden Rechenaufwand. BeiMonte-Carlo-Methoden skaliert die Rechenzeit zwar in einem Potenzgesetz, jedoch tritt bei fer-mionischen Systemen bei sehr tiefen Temperaturen oftmals das so genannte Vorzeichenproblemauf. Hier wächst der statistische Fehler stark an, so dass zur Verringerung von diesem wiederumeine größere Rechenzeit benötigt wird. Es lassen sich somit nur relativ kleine1 Systeme nume-risch exakt berechnen. Daher wurden Näherungen entwickelt, die auf die Berechnung von exaktlösbaren Teilsystemen, so genannten Cluster, zurückführen.Intuitiv naheliegend ist es, den Effekt von kurzreichweitigen Korrelationen durch die Bestim-mung von statischen und dynamischen Korrelationsfunktionen eines kleinen isolierten Clusterszu studieren [64]. Problematisch ist bei diesem direkten Cluster-Ansatz, dass Phasenübergängeund langreichweitige Ordnung nicht in endlich großen Systemen auftreten können. Dies führtezu einer Erweiterung dieses Ansatzes zu der so genannten Cluster Perturbation Theory (CPT;[72] ). Hier wird die Selbstenergie des Originalsystems, die alle relevanten Informationen überdie Wechselwirkungen enthält, durch die Selbstenergie eines Systems entkoppelter Cluster ap-proximiert. Diese Verallgemeinerung der Hubbard-I-Näherung [10] für endliche Cluster kann alsder führende Term in einer Entwicklung in der Hoppingamplitude angesehen werden.

Ein alternativer Ansatz wurde ausgehend von der Idee der klassischen Weiss’schen Molekular-feldtheorie [65] mit der dynamische Molekularfeldtheorie (DMFT) für Quantensysteme entwi-ckelt [66],[67]. Hier werden lokale Korrelationen exakt berücksichtigt und die nicht-lokalen durchein Molekularfeld, im Folgenden als Bad bezeichnet, näherungsweise bestimmt. Dabei wird dasOriginalsystem auf ein Störstellenmodell bestehend aus einem korrelierten Platz (U x 0) gekop-pelt an unendlich viele Badplätze ohne Wechselwirkung abgebildet und das Bad wird selbst-konsistent bestimmt. Aufgrund der Lokalität der Selbstenergie werden in der DMFT Effekteder nicht-lokalen kurzreichweitigen Korrelationen nicht berücksichtigt. Um solche Quantenf-luktuationen zu berücksichtigen, entwickelten sich daraus selbstkonsistente Methoden wie dieDynamical Cluster Approximation (DCA; [69] ) und die cellular DMFT [70]. Diese reduzierendie Komplexität des Originalsystems durch Abbildung auf ein Cluster eingebettet in ein Bad.Dabei unterscheiden diese beiden Methoden sich in der Natur des Cluster-Problems. So wer-den bei der im Ortsraum formulierten cellular DMFT Cluster mit offenen Randbedingungenbenutzt, die die Translationsinvarianz brechen. Bei der im k-Raum formulierten DCA bleibthingegen diese durch periodische Randbedingungen erhalten.Nun wäre es wünschenswert eine verallgemeinerte Theorie zu diesen Ansätzen zu finden. Diesist im Rahmen der Selbstenergiefunktionaltheorie (SFT; [24]) möglich. Durch die übergeordneteRolle der SFT lassen sich auch ganz neue Approximationen entwickeln. So entstand aus der SFT

1Die größtmögliche numerisch exakt lösbare Systemgröße hängt von der Komplexität des Modells und derLösungsmethode ab. So können mit der Lanczos-Methode unter Berücksichtigung sämtlicher SymmetrienSysteme mit 15 Plätzen numerisch exakt gelöst werden, per Exakter Diagonalisierung entsprechend weniger.Stochastische Methoden lassen Rechnungen für Systeme mit 100 Plätzen in hinreichender Genauigkeit undakzeptabler Rechenzeit zu. Im Vergleich zu einem Festkörper sind dies also noch immer sehr kleine Systeme.

21


die Variational Cluster Approximation (VCA; [25]). In dieser Approximation wird ausgenutzt,dass das großkanonische Potential Ω Σ als Funktional der Selbstenergie (SFT-Funktional),das eine Verknüpfung zwischen dem zu berechnenden System und einem System entkoppelterCluster schafft, bei der exakten Selbstenergie stationär ist. Dabei können die Plätze des Clus-ters, auf denen die lokale Wechselwirkung zwischen den Elektronen stattfindet, durchaus wie inder cellular DMFT in ein Bad eingebettet sein. Durch Variation der Cluster-Selbstenergie wirdder stationäre Punkt des SFT-Funktionals gesucht. Diese Optimierung führt dazu, dass Effekteaufgrund der endlichen Größe des Clusters teilweise kompensiert werden. Dadurch lassen sichmit dieser nicht-perturbativen Methode Phasenübergänge in Systemen stark korrelierter Elek-tronen, wie beispielsweise den Mottschen Metall-Isolator-Übergang, studieren.Die folgenden Abschnitte stellen eine Einführung in die SFT und VCA dar.

3.1 Das Luttinger-Ward-Funktional Φ

Für ein System von korrelierten Elektronen im Gleichgewicht existieren verschiedene Bezie-hungen zwischen statischen Größen, die die Thermodynamik des Systems, und dynamischenGrößen, die die Ein-Teilchen-Anregungen beschreiben. Statische Größen sind gegeben durch dasgroßkanonische Potential Ω und dessen Ableitung bezüglich der Temperatur T , dem chemischenPotential µ usw. Die Matsubara-Funktion G oder die Selbstenergie Σ sind hingegen dynamischeGrößen. Das Luttinger-Ward-Funktional ΦG liefert eine spezielle Beziehung zwischen stati-schen und dynamischen Größen. Es wurde erstmals 1960 von J.M. Luttinger und J.C. Ward[21] für einen Vielteilchen-Hamiltonian mit allgemeiner Zwei-Teilchen-Wechselwirkung konstru-iert, um eine diagrammatische Entwicklung der wechselwirkenden Green-Funktion G abzulei-ten. Das Luttinger-Ward-Funktional ergibt sich als Summe der Beiträge aller geschlossenen,zusammenhängenden, angezogenen Skelett-Diagramme der diagrammatischen Störungstheoriefür schwach gekoppelte Systeme:

Dabei stellen die Doppellinien den wechselwirkenden Propagator G und die gestrichelten Liniendie Wechselwirkung U dar. Die Auswertung der Diagramme ergibt dann:

Φ =ª

Qn=1

12nβQω

tr ΣnG .

Im Allgemeinen führt diese Skelett-Diagrammentwicklung nicht zu einem geschlossen Ausdruckfür ΦG, so dass die explizite funktionale Abhängigkeit auch für sehr einfache Systeme nicht be-kannt ist. Doch die folgenden Eigenschaften des Luttinger-Ward-Funktionals bilden die Grund-lage für die in Abschnitt 3.2 beschriebene Selbstenergiefunktionaltheorie.So existiert eine Verknüpfung des Luttinger-Ward-Funktionals mit dem großkonanischen Po-tential über das Funktional

Ω G = Φ G +Tr lnG −TrG−10 −G−1G (3.1.1)

mit der folgenden Definition der „Spur“

TrA = TQσQω

eiω0+ trA . (3.1.2)

22

3.1 Das Luttinger-Ward-Funktional Φ

Die „Spur“ (3.1.2) kann also analog zu (2.3.10) als eine in die Zeitdarstellung fouriertransfor-mierte Spur zur Zeit τ = 0− interpretiert werden.Eine wichtige Eigenschaft des Funktionals (3.1.1) ist, dass dieses für die exakte Matsubara-Funktion Gexakt stationär wird [7]:

δΩ GδG

WG=Gexakt

= 0 . (3.1.3)

Die Auswertung des Funktionals (3.1.1) an den stationären Punkten liefert dann das systems-pezifische großkanonische Potential Ω in den entsprechenden Phasen. Aus dieser Stationaritäts-eigenschaft lässt sich ein Variationsprinzip ableiten, indem die Matsubara-Funktion G einesReferenzsystems solang variiert wird, bis das Funktional (3.1.1), sofern dieses auswertbar seinsollte, einen stationären Punkt aufweist. Diese Idee soll im Rahmen der Selbstenergiefunktio-naltheorie im folgenden Abschnitt 3.2 nochmals aufgegriffen werden. Es wird dort allerdingseine alternative Formulierung dargestellt, in der das Luttinger-Ward-Funktional durch Termeeines Referenzsystems mit gleicher Wechselwirkung wie das Originalsystem ausgedrückt wird.

Eine weitere wichtige Eigenschaft des Luttinger-Ward-Funktionals ist, dass unabhängig vonder Dyson-Gleichung durch Funktionalableitung des Luttinger-Ward-Funktionals Φ nach derMatsubara-Funktion G die Selbstenergie Σ erzeugt werden kann2:

βδΦ G

δG=Σ G . (3.1.4)

Daher wird das Luttinger-Ward-Funktional Φ auch als erzeugendes Funktional der Selbstener-gie bezeichnet. Dieser Zusammenhang scheint plausibel, da das Entfernen eines wechselwirken-den Propagators aus einem beliebigen Φ-Diagramm zu einem entsprechenden Selbstenergie-diagramm (irreduzibles Skelett) führt. Allerdings gibt es für ein Diagramm n-ter Ordnung 2nMöglichkeiten ein entsprechendes Selbstenergiediagramm zu bilden.Im nicht-wechselwirkenden Fall verschwindet das Luttinger-Ward-Funktional:

ΦG 0 für U = 0 .

Neben der Selbstenergiefunktionaltheorie lässt sich mit Hilfe des Luttinger-Ward-Funktionalsunter anderem auch das Luttinger-Theorem [21] ableiten. Dieses auch als Luttinger-Summen-regel bekannte Theorem besagt, dass die Anzahl der Leitungselektronen gleich dem Fermi-Volumen im k-Raum multipliziert mit der Anzahl der reziproken Gitterpunkte in der erstenBrillouin-Zone ist. Eine unmittelbare Konsequenz daraus ist, dass für eine normale Fermi-Flüssigkeit das Volumen innerhalb der Fermi-Fläche unter Variation der Wechselwirkungsstärkeunverändert bleibt. Während das Fermi-Volumen eine Invariante ist, ändert sich im Allgemei-nen die Form der Fermi-Fläche.Des Weiteren lassen sich Näherungen mit Hilfe des Luttinger-Ward-Funktionals ableiten, fürdie die Selbstenergie, die Green-Funktion und das Luttinger-Ward-Funktional kosistent zuein-ander sind, d.h. dass sowohl Gleichung (3.1.4) als auch die Dyson-Gleichung (2.4.3) erfülltwerden. Solche Näherungen werden als erhaltende Näherungen bezeichnet. Dazu wird physika-lisch motiviert ein Satz von Φ-Diagrammen gebildet. Daraus lassen sich durch Entfernen eineswechselwirkenden Propagators die dazugehörigen Selbstenergiediagramme erzeugen. Über dieDyson-Gleichung lassen sich dann die Selbstenergie und die Green-Funktion iterativ bestimmen.

2Die Funktionalableitung nach der Matsubara-Funktion entspricht dem Entfernen eines wechselwirkenden Pro-pagators aus den Φ-Diagrammen.

23


3.2 Die SelbstenergiefunktionaltheorieDie 2003 von M. Potthoff veröffentlichte Selbstenergiefunktionaltheorie (SFT;[24]) ist ein sehrallgemeines Konzept bestehende Cluster-Ansätze zu verallgemeinern und liefert zudem nochdie Möglichkeit neuartige nicht-perturbative, thermodynamisch konsistente Approximationenzu entwickeln.Die zentrale Größe der SFT ist das großkanonische Potential, das als Funktional der Selbstener-gie konstruiert wird und für die exakte Selbstenergie stationär ist.Ausgehend von den Ideen von J.M. Luttinger und J.C. Ward [21], sowie von G. Baym und L.P.Kadanoff [22] der 1960er Jahre wird nach Gleichung (3.1.1) das großkanonische Potential alsFunktional der Matsubara-Funktion G gebildet:

Ω G = Φ G +Tr ln−G −Tr G−10 −G−1G,

wobei Φ G das Luttinger-Ward-Funktional ist. Dieses Funktional wird nach Gleichung (3.1.3)für die exakte Matsubara-Funktion stationär. Da aber im Allgemeinen der exakte funktionaleZusammenhang für Φ unbekannt ist, lässt sich das im vorhergehenden Abschnitt 3.1 erwähn-te Variationsprinzip bezüglich der Matsubara-Funktion nicht anwenden. Dieser Ansatz bleibtallerdings der Ausgangspunkt für die Selbstenergiefunktionaltheorie. Dazu geht man durchLegendre-Transformation zu einem Funktional der Selbstenergie Σ über und erhält:

Σ GÐG Σ .

Dabei muss jedoch angenommen werden, dass Σ G lokal invertierbar sei; das System sich alsoz.B. nicht an einem kritischen Punkt für einen Phasenübergang befindet [24].Das großkanonische Potential als Funktional der Selbstenergie ist dann:

Ω Σ = Tr ln − G−10 −Σ−1 + F Σ , (3.2.1)

wobei F Σ Φ G Σ − Tr Σ G Σ die Legendre-Transformierte des Luttinger-Ward-Potentials Φ G ist.Da das Luttinger-Ward-Funktional Φ G formal konstruierbar als Summe der Beiträge allergeschlossenen, zusammenhängenden angezogenen Skelett-Diagrammen ist, ist dieses nur vonder Wechselwirkung abhängig. Somit ist aber auch die Legendre-Transformierte F nur vonder Wechselwirkung abhängig. Haben nun Referenzsysteme H ′ die gleiche Wechselwirkung wiedas Originalsystem H, so ist F für diese Systeme universell und lässt sich Funktional (3.2.1)eliminieren, indem F Σ durch die entsprechenden Terme eines Referenzsystems ausgedrücktwird:

F Σ = Ω′ Σ +Tr ln− G′0−1 −Σ−1Damit ist also das großkanonische Potential des Originalsystems als Funktional der Selbstener-gie:

Ω Σ = Ω′ Σ −Tr ln − G−10 −Σ−1 −Tr ln− G′0−1 −Σ−1 . (3.2.2)

Man beachte, dass es für die Herleitung dieses Funktionals keinerlei Approximationen bedurfte.Aufgrund der zentralen Bedeutung in der Selbstenergifunktionaltheorie wird im Folgenden dasFunktional (3.2.2) als SFT-Funktional bezeichnet.Bemerkenswert ist, dass lediglich die freie Matsubara-Funktion G0 des Originalsystems be-kannt sein muss, sowie dessen Wechselwirkung, um geeignete Referenzsysteme auszuwählen,deren freie Matsubara-Funktion G′0 und Selbstenergie Σ numerisch exakt berechnet werden

24

3.3 Cluster-Approximationen innerhalb der SFT

können.

Durch die Legendre-Transformation folgt aus Gleichung (3.1.4):

βδF Σ

δΣ=G Σ .

Daraus lässt sich ableiten, dass das Funktional (3.2.2) bei der exakten Selbstenergie Σexakt desOriginalsystems stationär wird und es gilt die Euler-Gleichung

δΩ ΣδΣ

WΣ=Σexakt

= 0 . (3.2.3)

Der Wert des SFT-Funktionals (3.2.2) an einem stationären Punkt entspricht dem großkanoni-schen Potential in der entsprechenden Phase. Anzumerken sei noch, dass das SFT-Funktionalnur an den stationären Punkten eine physikalische Bedeutung besitzt und sonst nicht. Da-bei liefert wegen (2.1.6) der stationäre Punkt mit dem geringsten großkanonischen Potentialeine stabile Phase. Allerdings sollte bei der Betrachtung der stationären Punkte der trivialestationäre Punkt bei verschwindenen Variationsparameter vernachlässigt werden, sofern nicht-triviale stationäre Punkte existieren. Ein trivialer stationärer Punkt steht für eine Entkopplungdes Systems bezüglich dieses verschwindenen Variationsparameters. Dies würde sicherlich kei-ne optimierte Approximation für das Originalsystem darstellen. Abbildung 3.1 zeigt in vierverschiedenen Fällen welcher stationäre Punkt zu einer stabilen Phase gehört.

Abbildung 3.1: Schematische Darstellung von vier verschiedenen Verläufen des SFT-Funktionals. Die rotenPunkten geben die zu betrachtenen stationären Punkte an. Der zu der stabilen Phase gehö-rende stationäre Punkt ist mit einem Pfeil gekennzeichnet. Abb. entnommen aus Ref. [29]

3.3 Cluster-Approximationen innerhalb der SFTDas SFT-Funktional liefert zwar den exakten funktionalen Zusammenhang zwischen dem Ori-ginalsystem und einem Referenzsystem mit gleicher Wechselwirkung, jedoch ist die Auswertungdes SFT-Funktionals im Allgemeinen im höchsten Maße nicht trivial. Die entscheidende Ideestammt aus der Cluster Perturbation Theory (CPT; [72]). So wird, um die Komplexität des zuberechnenden Referenzsystem zu verringern, ein System von entkoppelten Cluster als Referenz-system betrachtet (Abbildung 3.2) und führt zu der Variational Cluster Approximation (VCA;[25]). Hier sind neben freien Green-Funktion G0 des Originalsystems lediglich noch die freieGreen-Funktion Gcluster

0 , das großkanonische Potential Ωcluster und die Selbstenergie Σcluster

eines Clusters zu berechnen. Aufgrund der Translationsinvarianz der Cluster innerhalb des sogenannten Supergitters bzw. durch die Extensivität des großkanonischen Potentials lassen sichaus den Werten für einen Cluster, die entsprechenden Werte für das als Referenzsystem die-nende System von entkoppelten Cluster berechnen. Diese Cluster-Approximation liefert ohne

25


Abbildung 3.2: Referenzsysteme für verschiedene Cluster-Approximationen für zweidimensionale Gitter-Modelle. Gefüllte Kreise: Onsite-Wechselwirkung. Durchgezogene Linien: Intraclusterhopping.Leere Kreise: Zusätzliche nb unkorrelierte Badplätze. Große Kreise: Bad mit nb = ª. Abb.entnommen aus Ref. [25].

Optimierung der Variationsparameter die gleichen Ergebnisse wie die CPT. Daher wurde dieVCA auch anfangs als variational CPT (vCPT) bezeichnet. Im Gegensatz zur CPT lassen sichmit der VCA durch die Optimierung von Parametern des Einteilchenanteils des HamiltoniansPhasenübergänge nachvollziehen und insbesondere symmetriebrechende Zustände beschreiben.Nicht nur die CPT lässt sich aus der SFT ableiten. Je nach Gestaltung der Cluster sind ver-schiedene Approximationen möglich. Dabei sind die Cluster zum einen charakterisiert durch dieAnzahl Nc der korrelierten Plätze in einem Cluster, auf denen die lokale Wechselwirkung zwi-schen den Elektronen stattfindet, und zum anderen durch nb zusätzliche unkorrelierte (UBad = 0)Badplätze pro korrelierten Platz. Diese sind durch ein Hopping der Stärke V , Hybridisierunggenannt, an die benachbarten korrelierten Plätze gekoppelt und vergrößern den Raum der Va-riationsparameter, um eine verbesserte Approximation zu erhalten. Abbildung 3.3 zeigt dieverschiedenen möglichen Approximationen in Abhängigkeit dieser beiden Parameter.

Abbildung 3.3: Verschiedene mögliche Clusterapproximationen innerhalb der SFT. Diese werden jeweils durchdie Clustergröße Nc und durch die Anzahl nb der Badplätze pro korrelierten Platz charakteri-siert. Damit lassen sich DMFT und cDMFT als Grenzfälle mit kontinuierlichem Bad innerhalbder SFT konstruieren. Abb. entnommen aus Ref. [28].

26

3.3 Cluster-Approximationen innerhalb der SFT

Die Dynamische Molekularfeldtheorie (DMFT; [66], [67]) ergibt sich für Nc = 1 und nb =ª, so-lange ein kontinuierliches Bad (nb =ª) benötigt wird, um eine beliebige lokale Green-Funktiondarzustellen. Aber schon allein die Wahl Nc = 1, nb <ª führt auf eine neue Klasse von Appro-ximationen, die so genannten Dynamcial Impurity Approximations (DIA; [24]). Diese Appro-ximationen sind zwar schlechter als die DMFT, bieten aber durch ihre Einfachheit aufgrundder endlichen Zahl der Badplätze die Möglichkeit schnelle Rechnungen mittels Exakter Dia-gonalisierung oder der Lanczos-Methode durchzuführen. Der einfachste Fall einer DIA ist füreinen einzigen zusätzlichen Badplatz gegeben (nb = 1). Diese Zwei-Platz-DIA lässt in der Nähedes kritischen Punktes für T = 0 analytische Rechnungen für den Mott-Übergang zu und lie-fert bereits Ergebnisse in relativ guter Übereinstimmung mit der DMFT. Mit wachsender Zahlder Badplätze nb konvergieren das großkanonische Potential, statische Größen und das gesamtePhasendiagramm gegen die Ergebnisse der DMFT [24].Auch die cellular DMFT (cDMFT; [70]) lässt sich aus der SFT ableiten, indem das Referenz-system aus einem Cluster mit Nc A 1 korrelierten Plätzen mit je einem kontinuierlichen Badnb = ª besteht. Analog zur DMFT und DIA erzeugt die cDMFT bessere Approximationenals die VCA. Allerdings existiert kein Cluster-Solver für den Temperaturnullpunkt T = 0, derErgebnisse für ein kontinuierliches Bad liefert, sodass wie in der VCA nur endlich viele Bad-plätze in die Rechnungen miteinbezogen werden können. Allerdings hat die Erfahrung gezeigt,dass die Konvergenz gegen das cDMFT-Ergebnis bereits mit sehr wenigen Badplätzen erreichtwird [31]. Da die cDMFT, genauso wie die DMFT, auf einer iterativen Berechnung bis zurSelbstkonsitenz beruht, ist die Verwendung der VCA mit einem geeigneten Algorithmus zumFinden der stationären Punkte sicherlich effizienter als die cDMFT. Auch ist das Auffindenvon Lösungen unterschiedlicher Phasen, insbesondere metastabiler Phasen, wesentlich einfa-cher und anschaulicher, da jeder stationäre Punkt eine Phase repräsentiert. In der cDMFT istein unendlichdimensionaler Parameterraum zu betrachten, in dem verschiedene Attraktoren dieunterschiedlichen Phasen repräsentieren. Gegen welchen Attraktor durch Iteration die Lösun-gen konvergieren, hängt davon ab, in welchem Einzugsgebiets die Startlösung liegt.Innerhalb der VCA sind auch neuartige Cluster-Approximationen je nach Beschaffenheit desverwendeten Clusters möglich. Durch die Verwendung eines Systems von entkoppelten Clus-tern als Referenzsystem, welches somit nicht die vollständige Translationinvarianz des Origi-nalsystems widerspiegelt, ist zu erwarten, dass die Finite-size-Effekte an der Clustergrenze amstärksten ausgeprägt sind. Um diese zu kompensieren, bieten sich Cluster mit platz- oder bin-dungsabhängigen Variationsparametern an. Dabei zeigt sich, dass lediglich die Variationspara-meter von Plätzen an der Clustergrenze entscheidend sind, um den Verlust der Itineranz durchdas fehlende Interclusterhopping auszugleichen [31]. Die Variationsparameter von Plätzen imInneren des Clusters weichen mit größer werdender Entfernung von der Clustergrenze immerweniger von den zu dem Originalsystem gehörenden Werten ab.Alle aus der VCA ableitbaren Approximation benutzen Cluster mit offenen Randbedingungen[25]. Damit besteht also in der VCA das Problem, dass durch die Konstruktion des Referenzsys-tems als System von entkoppelten Cluster mit offenen Randbedingungen die Translationssym-metrie des Originalgitters nicht erhalten bleibt. Dies ist ein generelles Problem von im Ortsraumformulierten Clusterapproximationen. Mit der Dynamical Cluster Approximation (DCA; [69])existiert eine im k-Raum formulierte Clustererweiterung der DMFT, die die Translationsinvari-anz des Originalsystems beibehält, indem Cluster mit periodischen Randbedingungen benutztwerden. Anzumerken ist, dass diese, auch wenn es zunächst wegen der periodischen Randbe-dingungen nicht offensichtlich erscheint, aus der SFT abgeleitet werden kann. Dazu sei auf [30]verwiesen. Da die DCA ebenfalls eine selbstkonsistente Methode mit kontinuierlichem Bad ist,ist deren Rechenaufwand ebenfalls größer als jener der VCA und das Auffinden metastabilerPhasen ist genauso schwierig wie in der cDMFT. Außerdem ist die über die DCA bestimmte

27


Selbstenergie Σk im k-Raum unstetig.

3.4 Numerische Auswertung des SFT-FunktionalsDa die gängigen Cluster-Solver die Green-Funktion statt der Selbsternergie des Referenzsystemsliefern, bietet sich an dieser Stelle eine Umformulierung des SFT-Funktionals (3.2.2) mit Hilfeder Dyson-Gleichung Σ =G′−10 −G′−1 an:

Ω = Ω′ +Tr ln − G−10 −G′−10 +G′−1−1 −Tr ln −G′= Ω′ −Tr ln 1 − G−10 −G′−10 G′

= Ω′ −1βQσ

ª

Qn=−ª

eiωn0+ tr ln 1 −V G′iωn . (3.4.1)

Hierbei wurde für die Umformulierung des SFT-Funktionals die aus der Cluster PerturbationTheory (CPT) bekannte Matrix V = t − t′ =G′

−10 −G−10 verwendet [72]. Diese enthält also die

Differenz zwischen dem „Intraclusterhopping“ des Originalsystems und des Referenzsystems,sowie auch das „Interclusterhopping“ des Originalsystems.Aufgrund der bisherigen Anwendung der VCA am Temperaturnullpunkt T = 0 (bzw. β ª)konnte man die Frequenzsummation in (3.4.1) in eine Integration überführen, die entweder voll-ständig numerisch oder auch teilweise analytisch ausgewertet wurde (vgl. Ref. [73]).Im Folgenden soll eine Variante zur Auswertung von (3.4.1) für endliche Temperaturen vorge-stellt werden, die auch teilweise analytische Ergebnisse beinhaltet und die die Berechnung derCluster-Matsubara-Funktion lediglich für sehr wenige Frequenzen benötigt.

Die Frequenzsummation im zweiten Term in (3.4.1) lässt sich auf nur positive Matsubara-Frequenzen beschränken, und es ist

I = −

1βQσ

ª

Qn=−ª

eiωn0+ tr ln 1 −V G′iωn

= − limη0

1βQσ

ª

Qn=0

eiωnη tr ln 1 −V G′iωn + e−iωnη tr ln 1 −V G′−iωn .

Aufgrund der Hermitizität der Matsubara-Funktion bei symmetrischer Hoppingmatrix t, alsoG′−iωn =G′iωn†, ist dann

I = − limη0

1βQσ

ª

Qn=0

eiωnη tr ln 1 −V G′iωn + e−iωnη tr ln 1 −V G′iωn† (3.4.2)

Um aber die Frequenzsummation für n > N0 numerisch zu realisieren wird I in einen niederfre-quenten Anteil I1ωc mit Summation über n > 0,1,2, ...nc und in einen HochfrequenzanteilI2ωc mit Summation über n > nc + 1, nc + 2, ... aufgeteilt. Also ist I = I1ωc+I2ωc. Dabeiist die Cutoff-Frequenz ωc = ωnc hinreichend groß zu wählen, so dass die Hochfrequenzasym-ptotik der Matsubara-Funktion erkennbar wird.Für den niederfrequenten Anteil I1 ist die Grenzwertbildung η 0 unproblematisch undder konvergenzerhaltende Faktor kann vernachlässigt werden, da limη0 eiωnη

= 1 für n >0,1,2, ...nc. Wird zusätzlich ausgenutzt, dass die Matrizen unter der Spur kommutieren, so-dass

tr ln 1 −V G′iωn = tr ln 1 −G′iωnV ,

28

3.4 Numerische Auswertung des SFT-Funktionals

lässt sich der niederfrequente Anteil noch weiter vereinfachen:

I1 = −1βQσ

nc

Qn=0

tr ln 1 −G′iωnV 1 −V G′iωn† . (3.4.3)

Durch diese Darstellung des Terms I1 muss lediglich die Spur vom natürlichen Logarithmus derhermiteschen Matrix 1 −G′iωnV 1 −V G′iωn† berechnet werden, indem die Logarith-men ihrer stets positiven Eigenwerte aufsummiert werden.Der Hochfrequenzanteil I2ωc muss hingegen weitestgehend analytisch berechnet werden, dader Grenzwert limη0 eiωnη für n ª numerisch nicht bestimmbar ist und keinesfalls trivialist, wie im Fall endlich großer Frequenzen.Zunächst betrachte man nochmals die Hochfrequenzentwicklung (2.3.23) der Matsubara-Funktion.Mit dieser Entwicklung der Matsubara-Funktion und der Potenzreihenentwicklung des natürli-chen Logarithmus ln1 − x = −x − x2~2 +Ox3 erhält man für den Logarithmus in (3.4.2) dieDarstellung

ln 1 −V G′iωn = −V M 0

iωn−

12V M 02 +V M 1

iωn2 +O iωn−3 . (3.4.4)

Werden die Terme der ersten beiden Ordnungen eingesetzt, wobei das Spektralmoment nullterOrdnung M 0 gerade gleich der Einheitsmatrix 1 ist, ergibt sich mithilfe der Euler-Formeleix= cosx + i sinx die folgende Näherung für den Hochfrequenzanteil:

I2 2β

limη0Qσ

ª

Qn=nc+1

sinωnηωn

trV −cosωnη

ω2n

tr12V 2+V M 1 . (3.4.5)

Für den Hochfrequenzkorrekturterm erster Ordnung bedeutet dies3:

−

2β

limη0Qσ

ª

Qn=nc+1

sinωnηωn

trV =1π

limη0Qσ

ª

Qn=nc+1

2πη

β

sinωnηωnη

trV

=1π

limη0QσSª

ωcηdω

sinωω

trV

=1πQσ

limη0π

2− Siωcη trV

= Qσ

12

trV . (3.4.6)

Somit ist dieser unabhängig von der inversen Temperatur β, der Wechselwirkungsstärke Uund der Cutoff-Frequenz ωc. Der Term zweiter Ordnung liefert hingegen einen von der Cutoff-

3Bei der Rechnung wird der Integralsinus benutzt: Six = R x0

sintt

dt = Pªν=0−1ν

2ν+12ν+1!x2ν+1.

29


Frequenz abhängigen Beitrag zum SFT-Funktional:

−

2β

limη0Qσ

ª

Qn=nc+1

cosωnηω2

n

tr12V 2+V M 1

= −

1π

limη0Qσ

ηª

Qn=nc+1

2πη

β

cosωnηωnη2 tr1

2V 2+V M 1

= −

1π

limη0Qσ

ηSª

ωcηdω

cosωω2

tr12V 2+V M 1

= −

1π

limη0

η12−π + 2Siωcη + 2

cosωcηωcη

Qσ

tr12V 2+V M 1

= −

1πωcQσ

tr12V 2+V M 1 . (3.4.7)

Insgesamt gilt nun damit für das SFT-Funktional:

Ω Ω′ −1βQσ

nc

Qn=0

tr ln 1 −G′iωnV 1 −V G′iωn†

+Qσ

12

trV −1

πωcQσ

tr12V 2+V M 1 . (3.4.8)

Allerdings ist für die Auswertung der Hochfrequenzkorrektur zweiter Ordnung die Kenntnis desSpektralmoments M 1 erforderlich. Die Bestimmung von M 1 ist jedoch nicht trivial (sieheAnhang A). Daher sollte diese umgangen werden. Das heißt, es ist die Cutoff-Frequenz so großzu wählen, dass der Hochfrequenzanteil gegen Pσ 1~2 trV konvergiert. Allerdings steigt derRechenaufwand des Cluster-Solvers mit größer werdender Cutoff-Frequenz ωc. In der Praxishat sich gezeigt, dass es effektiver ist, die Asymptotik des Niederfrequenzanteils I1 auszunut-zen und dessen Beitrag zu größeren Frequenzen zu extrapolieren anstatt für entsprechend vieleFrequenzen die Cluster-Matsubara-Funktion zu berechnen. Somit kann die Korrektur (3.4.7)auch vernachlässigt werden, wenn der Cluster-Solver die Matsubara-Funktion lediglich bei denersten wenigen Frequenzen auswertet, sofern dann bereits das Hochfrequenzverhalten von I1

erkennbar wird.

Zur Untersuchung des Frequenzverhaltens wird der führende Term der Hochfrequenzentwick-lung der Matsubara-Funktion in den Logarithmus in (3.4.3) eingesetzt un es ergibt sich diefolgende Approximation des Hochfrequenzverhaltens der einzelnen Frequanzsummanden:

tr ln 1 −G′iωnV 1 −V G′iωn† (3.4.9)

tr ln 1 + i1

ωnV 1 + i

1ωn

V †

ln1+xx

1ω2

n

trV 2. (3.4.10)

Die einzelnen Summanden fallen also im Hochfrequenzregime wie ω−2n ab. Neben der Imple-mentierung von (3.4.10) für die Frequenzsummanden bietet sich alternativ ein Fit des Hochfre-quenztails der Matsubara-Funktion G′iωn oder der Frequenzsummanden in (3.4.3) an, um dasHochfrequenzverhalten zu extrapolieren. Eine Diskussion einer sehr einfachen Implemetierungeines Fits durch die Konstruktion von Schätzern für die Fittingparameter mittels der Methode

30

3.5 Auswertung der Stationaritätsbedingung

der kleinsten Quadrate ist im Anhang C zu finden.

Lässt sich das Originalsystem von L Plätzen in ein System von entkoppelten Clustern mitjeweils Lc Plätzen eingebettet in einem Supergitter (Abbildung 3.2) teilen, was gerade eine dergrundlegenden Ideen der VCA ist, so kann die Translationsinvarianz des Supergitters ausgenutztwerden, um die zu betrachtende Matrixgröße von V und G′ auf die des Clusters zu reduzie-ren. Dabei besteht dann V = VIJlm aus Blöcken4, die jeweils einen Cluster repräsentieren.Durch die Translationsinvarianz des Supergitters lässt sich V durch eine Fouriertransformationbezüglich der Blöcke

VKlm =1

L~LcQIJ

e−iKI−J VIJlm =1

L~LcQI,J

e−iKI−J VI−J,0,lm

= QI

e−iKI VIlm

in Blockdiagonalgestalt bringen, wohingegen G′ bereits blockdiagonal ist mit G′Klm = Gclusterlm ,

da die Cluster entkoppelt sind. Insbesondere sind lediglich nur die verschiedenen direkt be-nachbarten Blöcke VIlm bei der Fouriertransformation zu berücksichtigen.5 Dabei beinhaltetnur der Block I = 0 das Intraclusterhopping. Man beachte, dass sich der Wert der Spur durchdie Fouriertransformation nicht ändert, jedoch sinkt der Aufwand der Auswertung von demNiederfrequenzanteil (3.4.3) der Frequenzsummation, da nur noch die Eigenwerte der Matrizen1 −G′

KiωnVK 1 −VKG′

Kiωn† blockweise aufsummiert werden müssen. Das heißt, es

kommt zu der Spin- und Frequenzsummation noch eine Summation über K hinzu und der Wertdes SFT-Funktionals ist approximativ gegeben durch:

Ω Ω′ −1βQσ

nc

Qn=0QK

tr ln 1 −G′KiωnVK 1 −VKG′Kiωn†

+

12

L

LcQσ

trVK −1

πωcQσQK

tr12VK

2+VKMK

1 . (3.4.11)

3.5 Auswertung der StationaritätsbedingungDurch die Variation der Selbstenergie des Referenzsystems und anschließender Auswertung desSFT-Funktionals (3.2.2) wird das Referenzsystem so optimiert, dass sich das SFT-Funktionaleinem stationären Punkt annähert. Anders als bei auf dem bekannten Ritzschen Variationsprin-zip basierenden Methoden kann hier keine obere Grenze für das exakte großkanonische PotentialΩ gefunden werden, und es können theoretisch sogar Abweichungen nach unten auftreten, auchwenn diese bislang noch nicht beobachtet wurden.Die Variation der Selbstenergien geschieht dabei durch die Veränderung von bestimmten aus-gewählten Variationsparametern des Ein-Teilchen-Anteils des Hamiltonians. Der Wechselwir-kungsanteil muss als Voraussetzung für die Anwendbarkeit der SFT unangetastet bleiben.Als Variationsparameter kommen Onsite-Energien, Hoppingamplituden oder fiktive symme-triebrechende Felder in Frage. Diese Parameter spannen einen Raum auf, in dem die Optimie-rung der Parameter stattfindet (Abbildung 3.4 unten). Im Prinzip sollten sämtliche denkbarenEin-Teilchen-Parameter variiert werden, um ein optimales Ergebnis zu erreichen.4Das Supergitter wird durch I und J indiziert, die Clusterplätze durch l und m. Diese können je nach Dimen-

sionalität des zu betrachtenden Systems auch Vektoren darstellen5Obwohl nur die direkt benachbarten Blöcke betrachtet werden, gibt es weiterhin genauso viele Werte für K

wie es Cluster gibt, also L~Lc.

31


Abbildung 3.4: Schematische Darstellung des Variationsprinzips aus der SFT: Durch Variation der Einteil-chenparameter t′ wird der Raum der Testselbstenergien Σt′ solang durchschritten, bis einstationärer Punkt des SFT-Funktionals gefunden wird. Da der Raum der Testselbstenergiennur einen Unterraum aller Selbstenergien darstellt, liefert der gefundende stationäre Punktlediglich eine Approximation, sofern der stationäre Punkt bzgl. des gesamten Σ-Raums nichtin dem untersuchten Unterraum liegt.

Um allerdings die aufwendige Suche nach einem stationären Punkt in einem hochdimensionalenParameterraum zu umgehen, wird die Zahl der Variationsparameter auf wenige physikalischmotivierte reduziert. Damit kann aber auch nur ein beschränkter Unterraum der Selbstenergienuntersucht werden (Abbildung 3.4 mitte). Die Wahl der Variationsparameter lässt sich oft ausder Geometrie des Clusters ableiten.

Die Variationsparameter werden nun im Folgenden in dem Parameter t′ zusammengefasst undes ist Σ = Σt′. Damit folgt aus der Euler-Gleichung (3.2.3) als Stationaritätsbedingung fürden Variationsparameter t′:

δΩ Σt′δt′

= 0.

Wird die Funktionalableitung auf der linken Seite ausgeführt, führt dies zu

TQωQαβ

G−10 −Σt′−1 −G′βα

δΣαβt′δt′

= 0. (3.5.1)

Trivialerweise ist diese Bedingung erfüllt, wenn das Referenzsystem die exakte Matsubara-Funktion des Originalsystems aufweist, also G′ =G Σt′ = G−10 −Σt′−1 und es ist somitt′ = t. Allerdings gehört der Punkt t′ = t in der Regel nicht zum Parameterraum, da t′ nur sogewählt werden kann, dass das Referenzsystem H ′ auch numerisch exakt lösbar ist.Geometrisch lässt sich Gleichung (3.5.1) als eine auf die Hyperfläche der Testselbstenergien pro-jizierte Dyson-Gleichung interpretieren. Dabei ist der Projektor δΣαβ~δt′ im Raum der Selbs-tenergien ein Vektor tangential zu der Hyperfläche der Testselbstenergien. Durch Bildung desSkalarproduktes mit diesem Projektor δΣαβ~δt′ wird somit die Projektion auf diese Hyperflächedurchgeführt.

32

3.6 Clustergeometrien

Suche nach stationären Punkten

Wird das SFT-Funktional effizient berechnet, so verbleibt noch die Suche nach den stationärenPunkten des Funktionals. Dazu bieten sich verschiedene numerische Strategien an. Für eineneindimensionalen Parameterraum ist der Aufwand gerade noch vertretbar, äquidistante Punk-te des Parameterraums für die Berechnung des Funktionals zu benutzen und den stationärenPunkt graphisch zu bestimmen. Es gibt jedoch effizientere Algorithmen zur Bestimmung einesstationären Punktes, sodass weitaus weniger Rechnungen benötigt werden.

In einem eindimensionalen Parameterraum sind in erster Linie die stationären Punkte durchExtrema des SFT-Funktionals gegeben. Ein möglicher und einfach zu implementierender Algo-rithmus für die Suche nach Extrema stellt das iterative Einschachteln (Bracketing) der Extremadar.Die Suche nach Minima soll hier nun kurz beschrieben werden, da der minimale stationärePunkt eine stabile Phase repräsentiert. Eine analoge Formulierung findet man auch für die Su-che nach Maxima.Zunächst werden zwei Werte für den Variationsparameter t′ benötigt mit ta < tb. Nun wird eindritter Parameterwert txn

(n soll den jeweiligen Iterationsschritt angeben) über den Mittelwertder beiden anderen konstruiert, also txn = ta + tb~2. Anschließend wird das SFT-Funktionalfür diese drei Parameter ausgewertet. Ist Ω Σtxn < Ω Σta und Ω Σtxn < Ω Σtb,so existiert ein Minimum im Intervall ta, tb. Durch Einfügen eines neuen Punktes soll einer derbisherigen Randpunkte des Intervalls ersetzt werden. Die Konstruktion dieses Punktes erfolgtdurch Intervallteilung mit Hilfe des Goldenen Schnittes. So sei

tc = ta + α tb − ta und td = ta + 1 − α tb − ta mit α =3 −º

52

.

Falls nun Ω Σtc < Ω Σtd wird tb = td gesetzt, sonst ist ta = tc.Dieses Vorgehen wird solange wiederholt bis die relative Unsicherheit den gewünschten Tole-ranzwert ε unterschritten hat, also tb − ta~tb + ta < ε. Dann ist txn ein Schätzer für denParameter des Minimums. Weist ein Modell mehere stationäre Punkte und damit auch meh-rere Phasen auf, sind die Startwerte der Optimierung entscheidend, welcher stationäre Punktgefunden wird. Des Weiteren wäre es problematisch, wenn Sattelpunkte auftreten würden, dadiese bei diesem Verfahren unberücksichtigt bleiben.Sattelpunkte treten zunehmend mit größer werdender Dimension des Parameterraums auf. Da-her ist bei einer Vielzahl von zu optimierenden Parametern die Downhill-Simplex-Methode [33]zu verwenden. Hier werden die lokalen Minima von SδΩ~δt′S2 gesucht. Von diesen Minima wer-den aber nur diejenigen nicht verworfen, für die der Gradient vom SFT-Funktional verschwindet.

3.6 Clustergeometrien

Für die numerische Auswertbarkeit des SFT-Funktionals (3.2.2) ist eine grundlegende Idee derVCA die Aufteilung des Originalgitters in ein System von entkoppelten identischen Clustern,das als Referenzsystem dient. Durch dieses Parkettieren des Gitters mit Cluster lässt sich einübergeordnetes so genanntes Supergitter finden. Dieses beschreibt die einzelnen Cluster alsPunkte eines Bravais-Gitters und führt aufgrund seiner Translationsinvarianz zu einer beque-meren Behandlung des Referenzsystems (vgl. Abschnitt 3.4). Abbildung 3.5 zeigt eine Auswahlvon möglichen Clusteraufteilungen eines zweidimensionalen Gitters. Allerdings ist die Geometrie

33


Abbildung 3.5: Mögliche Cluster um ein Gitter zu parkettieren: Die Zahlen geben die Anzahl der Plätze indem jeweiligen Cluster an. Rote Cluster führen auf Anordnungen mit Frustration.

der Cluster nicht unwesentlich für die Approximation. Die Cluster sollten die wichtigsten Sym-metrien des Originalsystems auch aufweisen. Die Translationsinvarianz innerhalb eines Clusterskann jedoch aufgrund der Forderung nach offenen Randbedingungen nicht realisiert werden.Die Erhaltung der Rotationssymmetrie ist aber zum Beispiel durchaus möglich.Neben der Erhaltung der Symmetrien liegt eine weitere Schwierigkeit bei ungeradzahligen Clus-tergrößen vor: Die hier vorliegende Kramers-Entartung kann problematisch für Monte-Carlo-Methoden, wie der in Kapitel 4 vorgestellte Algorithmus, werden. Diese sollen über das Kramers-Dublett mitteln. Jedoch kann es mitunter sehr lange dauern, bis das Umklappen in den jeweilsanderen Grundzustand realisiert wird. Entsprechend lang sollte die Markov-Kette gewählt wer-den, damit eine Mittelung über das Dublett eine hinreichend gute Genauigkeit erreicht.Weiterhin ist Frustration auch bei anderen Clustergeometrien möglich: Es ist aus dem GrenzfallU Q t, in dem das Hubbard-Modell auf das Heisenberg-Modell abgebildet werden kann, bekannt,dass das Hubbard-Modell eine langreichweitige antiferromagnetische Ordnung im Grundzustandbesitzt. Da jedoch das Referenzsystem aus identischen Cluster aufgebaut ist, kann bei unge-schickter Parkettierung des Gitters (z.B. durch die roten Cluster in Abbildung 3.5) magnetischeFrustration zwischen den Clustergrenzen zustande kommen. Der antiferromagnetische Grund-zustand wird somit unterdrückt.

3.7 Optimierung des Intraclusterhoppings

Die grundlegende physikalische Idee der VCA ist es, das fehlende Interclusterhopping desReferenzsystems durch die Variation von Parametern des Ein-Teilchen-Anteils des Cluster-Hamiltonians teilweise zu kompensieren. Wird zum Beispiel das Intraclusterhopping als Va-riationsparameter aufgefasst, dann wird es sicherlich einen nicht-trivialen stationären Punktbei Werten geben, die größer sind als das physikalische Hopping t. Es ist also t′opt A t. Da derVerlust der Itineranz durch das fehlende Interclusterhopping an der Clustergrenze die größtenAuswirkungen hat, weicht dort das optimale Hopping am stärksten vom physikalischen Hoppingab. Hingegen unterscheidet sich das optimale Intraclusterhopping von Plätzen weit im Innerengroßer Cluster kaum noch vom physikalischen Hopping des Originalsystems [31]. Allerdings fällt

34

3.8 Badplätze als zusätzliche Freiheitsgrade

mit größer werdenden Cluster das fehlende Interclusterhopping immer weniger ins Gewicht, so-dass die nötige Kompensation durch ein größeres Intraclusterhopping immer kleiner wird unddamit auch das optimale Intraclusterhopping t′opt, das gegen das physikalische Hopping t kon-

vergiert: t′optNcªÐ t. Die Qualität der Clusterapproximation ist somit in erster Linie durch

die Clustergröße Nc bestimmt. Im Vergleich zu einer direkten Cluster-Methode konvergiert dasVCA-Ergebnis deutlich schneller mit der Clustergröße gegen das exakte Ergebnis [31].Bei einer schwächeren Wechselwirkung ist der Vorteil der VCA stärker, da die direkte Cluster-Methode selbst bei U = 0 nur approximativ ist. Somit werden bei der VCA kleinere Clusterbenötigt um ähnliche Resultate zu finden. In Anbetracht des selbst bei stochastischen Cluster-Solvern in einem Potenzgesetz wachsenden Rechenaufwand ist dies ein klarer Fortschritt. Au-ßerdem lassen sich mit der VCA, anders als mit der direkten Cluster-Methode, auch Phasen-übergänge nachvollziehen. Als Nachteil kann lediglich angesehen werden, dass die Ergebnissefür die Grundzustandsenergie keine obere Grenze darstellen, da bislang kein Beweis existiert,dass das SFT-Funktional konvex ist. Die direkte Cluster-Methode hingegen liefert über dasRitzsche Variationsprinzip im Fall offener Randbedingungen strikte obere Grenzen. Um diesesProblem des SFT-Funktionals zu umgehen, wurde bereits die Konstruktion von konvexen SFT-Funktionalen durch Einführung von Korrekturen diskutiert [32].

Für stärkere Wechselwirkungen und somit stärker lokalisierte Elektronen ist das Fehlen desInterclusterhoppings weniger entscheidend [31] und die Variation des Intraclusterhoppings lie-fert als einen sich vom physikalischen Hopping nur unwesentlich unterscheidenden Wert. DieOptimierung ist somit vor allem kleine Cluster mit kleinem U wichtig. Hier ist die VCA somitder CPT überlegen, deren Ergebnisse durch Setzen von t′ = t mit der VCA reproduziert werdenkönnen.Wird nun die Wechselwirkungsstärke U verringert, weicht also das optimale Intraclusterhoppingimmer mehr vom physikalischen Hopping t des Originalsystems ab. Gleichzeitig wird aber auchdas SFT-Funktional immer flacher. Schließlich ist für U 0 der Wert des optimalen Hoppingsfür t′ A t irrelevant, sodass die Selbstenergie Σ für jedes Intraclusterhopping t′ verschwindet:Σω 0.

3.8 Badplätze als zusätzliche Freiheitsgrade

Eine Möglichkeit um die Anzahl der Freiheitsgrade bei der Variation des SFT-Funktionals zuerhöhen, ist in Analogie zur cDMFT unkorrelierte (UBad = 0) Badplätze dem Cluster hinzuzufü-gen. Dabei stellen dann neben den Onsite-Energien εc der korrelierten Plätze und dem Hoppingt′ zwischen ihnen die Onsite-Energien εb, sowie das Hopping t′′ zwischen den Badplätzen selbstbzw. das Hopping V zwischen den korrelierten Plätzen und den Badplätzen weitere Variations-parameter dar (siehe Abbildung 3.6). Da keine Wechselwirkung auf den Badplätzen existiert,bleibt auch der Wechselwirkungsanteil des Hamiltonians unverändert, wie es von der SFT ge-fordert wird. Damit enthält die Selbstenergiematrix auch nur in dem Block, der die korreliertenPlätze repräsentiert, von Null verschiedene Einträge.

Aus Dimensionsgründen müssen dem Originalsystem allerdings auch fiktive entkoppelte Bad-plätze hinzugefügt werden. Ihre Onsite-Energie εorig

b ist dabei frei wählbar, da deren Beitragnach Berechnung des SFT-Funktionals wieder abgezogen werden muss. Dazu betrachte mandie Zustandssumme der Badplätze, die aufgrund der Entkopplung der Badplätze einer freien

35


Abbildung 3.6: Beispiel für einen 2D-Cluster mit Badplätzen: die hier auftretenden Variationsparameter sindt′, t′′, V , εc und εb

Zustandssumme gleicht:

ΞBad = 1 + 2 e−βεorigb−µ+ e−2βεorig

b−µ. (3.8.1)

Nach (2.1.1) folgt somit für den vom SFT-Funktional abzuziehenden Beitrag der Badplätze:

ΩBad = −1β

lnΞBad. (3.8.2)

Um einen hochdimensionalen Variationsparameterraum zu vermeiden, sollten nur sinnvolle Teil-räume betrachtet werden und für die Optimierung nur gering förderliche Variationsparamterausgeschlossen werden. Es zeigt sich, dass oftmals das Hopping t′′ zwischen den Badplätzennur eine vernachlässigbare Korrektur liefert. Liegt Teilchen-Loch-Symmetrie vor, kann der Va-riationsparameterraum noch weiter reduziert werden: Wird nur ein zusätzlicher Badplatz prokorrelierten Platz gewählt, so wird dessen Onsite-Energie durch die Teilchen-Loch-Symmetrieauf das chemische Potential fixiert: εb = µ = U~2. Die Onsite-Energie der korrelierten Plätzeverschwindet hingegen: εc = 0, und es verbleibt nur die Optimierung bezüglich t′ und V . Fürzwei mit gleichem V an einem korrelierten Platz gekoppelte Badplätze sind die Onsite-Energiender beiden gegeben durch: εb = µ ∆ε, so dass t′, V und ∆ε die zu optimierenden Variations-parameter darstellen.Für Cluster-Approximationen mit Nc A 1 sollten die Badplätze für nicht-gleichwertige korre-lierte Plätze unterschiedlich sein und somit deren Werte separat voneinander optimiert werden.Es zeigt sich, dass Badplätze am Clusterrand effizienter sind [31], um das vernachlässigte In-terclusterhopping zu kompensieren, als die an die Clustermitte gekoppelten Badplätze. So sindin erster Linie Clustergeometrien für die VCA zu benutzen, bei denen die Badplätze nur an dieäußeren korrelierten Plätze koppeln, um den Parameterraum weiter einzuschränken.Insgesamt sei anzumerken, dass die Variation der Hybridisierungsstärke V effektiver ist als diedes Intraclusterhoppings t′ [31]. Allerdings wird mit zunehmender Clustergröße Nc die Appro-ximation durch ein System von entkoppelten Cluster immer besser, da der Einfluss des Fehlensder Interclusterhoppings immer geringer wird. So liefert die Optimierung durch Hinzufügen ei-ner Hybridisierung zu Badplätzen für große Cluster nicht wesentlich bessere Approximationen.Im Limes Nc ª ist natürlich zu erwarten, dass das Referenzsystem das Originalsystem repro-duziert und somit die Badplätze entkoppeln (Vopt = 0). Andererseits wäre in diesem Grenzfallauch ein endlicher Wert für die optimale Hybridisierungsstärke zu Badplätzen am Clusterranddenkbar. Da dann jedoch keine relevante Änderung der Approximation hervorgerufen wird, istdann die Optimierung im Wesentlichen irrelevant.

36

4 Der stochastische Cluster-Solver

Das entscheidende Problem bei der Lösung von wechselwirkenden Vielteilchensystemen liegt indem exponentiellen Wachstum des Hilbert-Raumes mit der Zahl Nc der Gitterplätze. Die Zahlder Basiszustände ist dabei gegeben durch 4Nc . Eine exakte Lösung durch Diagonalisierung istdaher für große Systeme aussichtslos, da die benötigte Rechenzeit und Speicher durch das expo-nentielle Wachstum des zu diagonalisierenden Hamiltonians nicht akzeptabel sind. Auch wenndurch Ausnutzung von Symmetrien und der Lanczos-Methode die Dimension reduziert werdenkann, ist diese numerisch exakte Lösungmethode für das Hubbard-Modell füllungsabhängig aufweniger als 15 Plätze begrenzt.Stochastische Methoden, wie die Vielzahl an Quanten-Monte-Carlo-Algorithmen [42], liefern je-doch einen alternativen Ansatz zur Lösung von großen Vielteilchensystemen mit 100 Plätzen,da hier die Rechenzeit in einem Potenzgesetz skaliert. Allerdings ist der Vorfaktor groß, sodasssolche stochastische Methoden auch nur für große Systeme sinnvoll sind.Ein Nachteil von stochastischen Methoden ist, dass sie einen statistischen Fehler besitzen, derfür fermionische Systeme füllungsabhängig durch das so genannte Vorzeichenproblem exponen-tiell mit der Anzahl der Plätze Nc und der inversen Temperatur β anwachsen kann.

In diesem Kapitel soll nun der Einsatz einer stochastischen Methode als Cluster-Solver für dieVCA vorgestellt werden. Dazu werden zunächst die Grundlagen von Monte-Carlo-Methodenbasierend auf Markov-Ketten vorgestellt, die in der anschließend dargelegten weak-couplingContinuous Time - Quantum Monte Carlo-Methode (wcCT-QMC) [48] Anwendung finden.Diese dient dann als Fundament für den stochastischen VCA-Cluster-Solver, der eine analog zudem Wang-Landau-Algorithmus modifizierte wcCT-QMC-Methode darstellt.

4.1 Grundlagen der Markov-Ketten-Monte-Carlo-MethodenIst der Erwartungswert bezüglich der Wahrscheinlichkeitsverteilung q einer Funktion O vonZufallsvariablen X auf dem Ereignisraum E, im Folgenden Zustandsraum genannt, also

`Oeq = Qi>E

Oi qi, (4.1.1)

nicht explizit berechenbar, so muss nach einer geeigneten Approximation für diesen gesuchtwerden.Eine Möglichkeit wäre es, unabhängige Zufallszahlen vom Computer gemäß der Verteilung qerzeugen zu lassen. Nach dem starken Gesetz der großen Zahlen konvergiert der Mittelwert vonFunktionswerten der Zufallsvariablen Xk,

ON =1N

N

Qk=1

OXk, (4.1.2)

fast sicher1 gegen den gesuchten Erwartungswert. Der Mittelwert einer großen Zahl von solchenZufallszahlen stellt somit eine Approximation für den Erwartungswert dar.1Fast sichere Konvergenz bedeutet hierbei: P limNªON = `Oeq = 1 .

37


Falls allerdings die Normierungskonstante der Verteilung q, also Pi>E qi, deren Rolle in derPhysik die Zustandssumme übernimmt, nicht bekannt und aufgrund der Größe des Zustands-raumes nicht effektiv bestimmbar ist, muss eine Methode zur Erzeugung von Zufallszahlenmit Verteilung q gefunden werden, die auf der Verwendung der unnormierten Verteilung ba-siert. Dies ist mit Hilfe einer Markov-Ketten-Monte-Carlo-Methode möglich, speziell mit demMetropolis-Algorithmus, bei dem nur der Quotient qi~qj für alle i, j > E bekannt sein muss.Die Normierungskonstante kürzt sich also weg.

Die folgenden Abschnitte werden sich mit Markov-Ketten und ihren Klassifikationen beschäfti-gen, um die Voraussetzungen für eine Erzeugung von näherungsweise q-verteilten Zufallszahlendarzustellen. Da hier allerdings das starke Gesetz großer Zahlen die Approximation durch dieMittelwertbildung nicht mehr gewährleistet, weil die Zufallsvariablen nicht mehr unabhängigund identisch verteilt sind, wird eine andere Rechtfertigung für diese Approximation benötigt:der Ergodensatz.

4.1.1 Markov-KettenEs sei X = Xt t > N eine Familie von Zufallsvariablen, also ein stochastischer Prozess, beidem Xt im Folgenden den zufälligen Zustand eines zu beschreibenden Systems zum Zeitpunktt > N repräsentiere.Ein stochastischer Prozess X heißt Markov-Kette, wenn für alle Zeiten 0 B t0 < t1 < ... < tn, tk >N, und beliebige Zustände i0, i1, ..., in aus einem höchstens abzählbaren Zustandsraum E diebedingte Wahrscheinlichkeit, dass sich das System zur Zeit tn im Zustand in befindet, wennes sich zum Zeitpunkt tn−1 im Zustand in−1, zum Zeitpunkt tn−2 im Zustand in−1,..., zumZeitpunkt t0 im Zustand i0 befand, also

P Xtn = in SXtn−1 = in−1, Xtn−2 = in−2, ..., Xt0 = i0 ,unabhängig von den Zuständen zur Zeit tn−2, tn−3, ..., t0 ist, d.h. wenn

P Xtn = in SXtn−1 = in−1,Xtn−2 = in−2, ...,Xt0 = i0 = P Xtn = in SXtn−1 = in−1 (4.1.3)

gilt. Die „Vergangenheit“ vor tn−1 hat also keinen Einfluss auf die Eintrittswahrscheinlichkeitvon Xtn und die weitere Entwicklung des Modellsystems.Gleichung 4.1.3 ist äquivalent dazu, dass für n > N, n C 2, und i1, ..., in > E gilt:

P Xn = in SXn−1 = in−1, Xn−2 = in−2, ..., X0 = i0 = P Xn = in SXn−1 = in−1 . (4.1.4)

Im Folgenden wird der Einfachheit halber mit dieser Definition gearbeitet.Gilt nun für alle m,n > N und alle i, j > E

P Xm+n = j SXn = i = P Xm = j SX0 = i ,d.h. ist die linke Seite unabhängig von n, so heißt die Markov-Kette homogen. Diese Wahr-scheinlichkeit wird auch als m-Schritt-Übergangswahrscheinlichkeit bezeichnet. Insbesondereerhält man in einer homogenen Markov-Kette die Ein-Schritt-Übergangswahrscheinlichkeit

P Xn+1 = j SXn = i = P X1 = j SX0 = i = Tij . (4.1.5)

Offensichtlich gilt Tij C 0 und Pj Tij = 1 und die Übergangsmatrix T = Tij ist somit einestochastische Matrix.Für die m-Schritt-Übergangswahrscheinlichkeit gilt:

P Xm = j SX0 = i = T mij ,

38

4.1 Grundlagen der Markov-Ketten-Monte-Carlo-Methoden

d.h. die m-Schritt-Übergangswahrscheinlichkeiten erhält man durch Potenzieren der Übergangs-matrix T .

Im Folgenden seien alle betrachteten Markov-Ketten homogen.

Sei nun der stochastische Vektor pn = pni = P Xn = i i > E die Zustandsverteilungvon X zur Zeit n, dann gilt nach dem Satz der totalen Wahrscheinlichkeit

pnj =Q

i

pn−1i Tij ,

d.h. pn = pn−1T . Mit vollständiger Induktion lässt sich daraus zeigen, dass die Zustandsver-teilung von X zur Zeit n durch die Startverteilung p0 und die Übergangsmatrix T eindeutigfestgelegt ist:

pn = pn−1 T = ... = p0 T n.

4.1.2 Ergodizität und stationäre Verteilung von Markov-KettenZiel ist es im Folgenden, solche Markov-Ketten zu charakterisieren, die unabhängig von derStartverteilung stets gegen eine bestimmte Grenzverteilung konvergieren, d.h. solche Markov-Ketten, die sich in einem „Gleichgewichtszustand“ einschwingen und dann „stationäres“ Verhal-ten zeigen. Diese Eigenschaft erfüllen genau „ergodische“ Markov-Ketten.

Es sei X eine Markov-Kette mit Zustandsraum E und Übergangsmatrix T .

Ein stochastischer Vektor2 q = qi i > E heißt stationäre Verteilung (Gleichgewichtsvertei-lung) von X, wenn

q = q ċ T , (4.1.6)

d.h. wenn q ein linker Eigenvektor zum Eigenwert 1 der Übergangsmatrix T ist.

Die Bezeichnung stationäre Verteilung bzw. Gleichgewichtsverteilung lässt sich so erklären,dass die Markov-Kette, wenn sie einmal diese Zustandsverteilung angenommen hat, diese nichtmehr verlassen wird: Ist pn = q für ein n > N, so gilt auch pn+1 = pnT = q T = q, alsopm = q für alle m C n. Wird die Markov-Kette also unter einer stationären Verteilung p0 = qgestartet, so ändert sich die Zustandsverteilung nicht mit der Zeit. Es kann durchaus der Fallsein, dass eine Markov-Kette mehrere oder auch keine stationäre Verteilungen hat. Allerdingsgibt es eine bestimmte Klasse von Markov-Ketten, für die eine eindeutig bestimmte stationäreVerteilung existiert. Dies sind genau irreduzible und positiv rekurrente Markov-Ketten:

(i) Die Markov-Kette X heißt irreduzibel, wenn je zwei Zustände i, j > E mit positiver Wahr-scheinlichkeit gegenseitig erreichbar sind, d.h. wenn gilt:

∀i, j > E § n > N T nij = P Xn = j SX0 = i A 0.

Der Zustandsraum darf also nicht in Unterräume zerfallen, die von der Kette nicht mehrverlassen werden. Es können zwar Ein-Schritt-Übergangswahrscheinlichkeiten zwischenZuständen auch Null sein, jedoch muss es zwischen zwei beliebigen Zuständen mindestenseinen Weg (mit n Schritten) mit nicht-verschwindender n-Schritt-Übergangswahrscheinlich-keit geben.

2Für einen stochastischer Vektor gilt: Pi>E qi = 1 .

39


(ii) Ist die erwartete Rückkehrzeit eines Zustands endlich, so wird dieser Zustand als positivrekurrent bezeichnet. Gilt dies für alle Zustände des Zustandsraumes, so heißt die Markov-Kette X positiv rekurrent.

Ist der Zustandsraum E endlich, so muss es mindestens einen positiv rekurrenten Zustand i > Egeben, denn irgendwo muss der Prozess sich stets aufhalten und es stehen für unbegrenzt vieleZeitpunkte nur endlich viele Aufenthaltsorte zur Verfügung. Außerdem ist positive Rekurrenzeine sogenannte „Klasseneigenschaft“, d.h. sind zwei Zustände mit positiver Wahrscheinlichkeitgegenseitig erreichbar und ist einer von ihnen positiv rekurrent, so gilt dies auch für den anderen.

Erfüllt die Markov-Kette eine weitere Eigenschaft, die Aperiodizität, so konvergiert die Zu-standsverteilung (unabhängig von der Startverteilung p0) punktweise gegen diese eindeutigbestimmte stationäre Verteilung q, d.h. limnª p

ni = qi für alle i > E.

Die Markov-Kette X heißt aperiodisch, wenn sie sich nicht in Zyklen fangen kann und dadurchdas Auftreten bestimmter Zustände zu bestimmten Zeitpunkten ausgeschlossen ist, formal aus-gedrückt:Man betrachte die Menge der Anzahl der Schritte n > N, in denen man mit positiver Wahr-scheinlichkeit aus einem Zustand i > E nach i zurückkehren kann:

Ni = n > N T nii A 0 .Der Zustand i heißt aperiodisch, wenn der größte gemeinsame Teiler der Elemente aus Ni, diePeriode, gleich Eins ist. Gilt dies für jeden Zustand i > E, so heißt X aperiodisch.

Mit diesen drei Eigenschaften haben wir eine wichtige Klasse von Markov-Ketten eingeführt:Eine irreduzible, positiv rekurrente und aperiodische Markov-Kette heißt ergodisch3.

Zusammenfassend ergibt sich: Ist X ergodisch, dann gilt:

(i) Es gibt eine eindeutig bestimmte stationäre Verteilung q von X.

(ii) Die Zustandsverteilung pn konvergiert punktweise gegen die stationäre Verteilung w

unabhängig von der Startverteilung p0, d.h. limnª pni = qi für alle i > E.

Ergodensatz: Ist X eine ergodische Markov-Kette mit stationärer Verteilung q, so tritt dasKonvergenzresultat

limnª

1n

n

Qi=1

OXi = Qj>E

Aj qj = Òeqmit Wahrscheinlichkeit 1 auf.Dieser „Ergodensatz“ stellt das zentrale Resultat dieses Abschnitts dar, der es erlaubt einengesuchten Erwartungswert einer Observablen O bezüglich einer bestimmten vorgegebenen Ver-teilung q, also

Òeq = Qj>E

Oj qj,

durch den Mittelwert ON einer großen Anzahl N von Realisierungen einer ergodischen Markov-Kette X = Xi i > N mit stationärer Verteilung q zu approximieren:

Àeq AN =1N

N

Qi=1

AXi für großes N. (4.1.7)

3In der Physik-Literatur wird oft „Ergodizität“ als Synonym für die „Irreduzibilität“ einer Markov-Kette aufeinem endlichen Zustandsraum verwendet und die Existenz einer eindeutig bestimmten stationären Zustands-verteilung zusätzlich gefordert.

40


Anzumerken ist, dass der hier vorgestellte Ergodensatz auch bereits schon für eine irreduzi-ble und positiv rekurrente Markov-Kette gilt. Die Forderung der Ergodizität stellt allerdingssicher, dass die Zustandsverteilung der Markov-Kette gegen die stationäre Verteilung q konver-giert. Diese Konvergenz ist wünschenswert, da dadurch die Realisierungen nach ihrem Gewichtausgewählt werden (Importance-Sampling) und somit eine Verbesserung der Approximationhergestellt wird.Wie diese Markov-Kette mit einer vorgegebenen stationären Verteilung zu konstruieren ist, wirdim folgenden Abschnitt mit Hilfe des Metropolis-Algorithmus erläutert.Eine hinreichend große Stichprobe von Realisierungen einer entsprechenden Markov-Kette kannsomit als Approximation für den zu berechnenden Erwartungswert angesehen werden.

4.1.3 Metropolis-AlgorithmusDie erste Veröffentlichung zur die Thematik der Markov-Ketten-Monte-Carlo-Methode erschien1953 als Artikel von N. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, A.H.Teller und E. Tel-ler [39], der in Fachkreisen auch den Namen M(RT)2 erhalten hat. Der von ihnen vorgeschlageneAlgorithmus zur Konstruktion einer Markov-Kette zu vorgegebener stationärer Verteilung, wiesie beispielsweise nach dem Ergodensatz zur Approximation eines Erwartungswertes benötigtwird, ist heute als Metropolis-Algorithmus bekannt. W.K. Hastings gelang es 1970 [40] denMetropolis-Algorithmus auf eine größere Klasse von Markov-Ketten-Monte-Carlo-Algorithmenzu verallgemeinern, wodurch diese den Namenszusatz „Hastings“ bekamen. In Literatur derstatistischen Physik steht häufig die Bezeichnung „Monte-Carlo-Methode“ als Synonym für dieAnwendung eines Metropolis-Hastings-Algorithmus.

Durch den Ergodensatz ist eine Approximationsmöglichkeit mit Hilfe von Markov-Ketten fürErwartungswerte bezüglich einer Verteilung q gegeben. Mit dem Metropolis-Algorithmus er-zeugt man nun, diese Markov-Kette von der nur bekannt ist, dass ihre Zustandsverteilunggegen q konvergiert. Damit eine eindeutige stationäre Verteilung existiert und die Zustands-verteilung auch gegen diese konvergiert, muss X ergodisch sein. Der Metropolis-Algorithmuskann auf Prozesse angewendet werden, deren Verhältnis zwischen Wahrscheinlichkeiten von jezwei Zuständen bekannt ist. Man muss also nicht einmal die exakte Verteilung kennen, wasein klarer Vorteil gegenüber der Monte-Carlo-Methode mit unabhängig und identisch verteiltenZufallsvariablen ist.Ein Problem stellt nun die Realisierung der Markov-Kette X dar, da die Übergangsmatrix Tgeeignet konstruiert werden muss, damit die Zustandsverteilung pn gegen die gewünschte sta-tionäre Verteilung w konvergiert.Eine hinreichende Bedingung dafür, dass die Markov-Kette die gewünschte stationäre Vertei-lung besitzt, ist, dass ihre Übergangsmatrix T das folgende detaillierte Gleichgewicht („detailedbalance“) bezüglich der vorgegebenen stationären Verteilung q erfüllt:

qiTij = qjTji für alle i, j > E. (4.1.8)

Es sollen also zwei beliebige Zustände zueinander im Gleichgewicht stehen. Eine Markov-Kette,die das detaillierte Gleichgewicht erfüllt, heißt reversibel. Dass diese Bedingung die stationäreVerteilung liefert, ist leicht einzusehen:

Qi>E

qi Tij = Qi>E

qj Tji = qj Qi>E

Tji = qj .

Damit erfüllt q also (4.1.6) und ist somit eine stationäre Verteilung einer Markov-Kette mitÜbergangsmatrix T .

41


Das detaillierte Gleichgewicht liefert aber offensichtlich keine eindeutige Festlegung der Über-gangsmatrix T . Eine Möglichkeit besteht durch den folgenden Ansatz:Es sei M die Übergangsmatrix einer beliebigen irreduziblen und aperiodischen Markov-Ketteauf dem Zustandsraum E (mit Mij = 0 für möglichst viele j > E), dann ist die ÜbergangsmatrixT bezüglich M und q definiert durch

Tij =

¢¦¤MijAij , falls i x j,

1 −Pk>E,kxi MikAik, falls i = j.(4.1.9)

Zur Simulation einer Markov-Kette X, die gegen q konvergiert, kann man nun ausgehend voneiner Referenzkette mit Übergangsmatrix M auf dem gleichen Zustandsraum E, wie folgt denMetropolis-Algorithmus verwenden:Schlägt die Markov-Kette mit Übergangsmatrix M einen Übergang vom aktuellen Zustandi > E nach j > E vor, so wird dieser Vorschlag mit Wahrscheinlichkeit

Aij =minMji qj

Mij qi,1 (4.1.10)

akzeptiert. Mit Wahrscheinlichkeit 1−Aij wird der Übergang von i nach j hingegen nicht akzep-tiert und die Markov-Kette X verbleibt im Zustand i. Man beachte, dass lediglich der Quotientder gewünschten stationären Verteilung für die an dem Übergang beteiligten Zustände bekanntsein muss. Somit wird die aufwendige Berechnung der Normierung im Metropolis-Algorithmusumgangen.Wird M symmetrisch gewählt, so erhält man den ursprünglichen Metropolis-Algorithmus nach[39].Es ist leicht einzusehen, dass dieser Ansatz für die Übergangmatrix T das detaillierte Gleich-gewicht erfüllt und somit die Verteilung q stationär ist:

Fall 1: Mji qj

Mij qiA 1

Aij = 1, Aji =Mij qi

Mji qj

Tij

Tji=

Mij Aij

Mji Aji=

Mij

Mji

1Mji qj

Mij qi

=

qj

qi

Fall 2: Mji qj

Mij qi< 1

Aij =Mji qj

Mij qi, Aji = 1

Tij

Tji=

Mij Aij

Mji Aji=

Mij

Mji

Mji qj

Mij qi

1=

qj

qi

Fall 3: Mji qj

Mij qi= 1

Aij = Aji = 1

Tij

Tji=

Mij Aij

Mji Aji=

Mij

Mji=

qj

qi

42


Aus der Irreduzibilität und Aperiodizität der Referenzkette mit Übergangsmatrix M folgt auchdie Irreduzibilität und Aperiodizität der Markov-Kette X [38]. Aufgrund der Existenz einer sta-tionären Verteilung folgt aus der Irreduzibilität und Aperiodizität der Markov-Kette X auch diepositive Rekurrenz nicht-endlicher Zustandsräume E und damit die Ergodizität der Markov-Kette X, d.h. die Zustandsverteilung konvergiert unabhängig von der Startverteilung gegendie stationäre Verteilung q. Insbesondere lässt sich dadurch über Importance-Sampling derErwartungswert einer Observablen nach (4.1.7) durch den Mittelwert der Realisierungen derMarkov-Kette approximieren.

Der Simulationsablauf von Algorithmen des Metropolis-Hastings-Typs lässt sich wie folgt zu-sammenfassen:

1. Wähle einen Anfangszustand X0 = i

2. Schlage einen neuen Zustand j mit Wahrscheinlichkeit Mij zufällig vor

3. Berechne die Akzeptanzwahrscheinlichkeit Aij für den vorgeschlagenen Zustands-wechsel

4. Generiere eine Zufallszahl r > 0,1 gleichverteilt

5. Akzeptiere: xk+1 = j falls r < Aij

Verwerfe: xk+1 = i sonst

6. Fahre mit 2. fort bis hinreichend viele Realisierungen der Observablen vorhandensind, deren Erwartungswert durch (4.1.7) anschließend approximiert wird.

Bemerkungen zum detaillierten Gleichgewicht

Das detaillierte Gleichgewicht stellt eine sehr starke Bedingung an die Übergangswahrschein-lichkeiten Tij dar, jedoch keine notwendige Bedingung dafür, dass die Zustandsverteilung gegendie gewünschte stationäre Verteilung konvergiert. Es gibt daher effizientere Algorithmen als diedes Metropolis-Hastings-Typs. Diese weisen wesentlich höhere Akzeptanzwahrscheinlichkeitenauf und erreichen wesentlich schneller die stationäre Verteilung, ohne jedoch die Bedingungdes detaillierten Gleichgewichts zu erfüllen. Um die Freiheitsgrade für die Ableitung von Al-gorithmen, die eine Konvergenz gegen die stationäre Verteilung aufweisen sollen, zu erhöhen,muss also von der strikten Bedingung (4.1.8) für jeden Schritt auf der Markov-Kette abgesehenwerden. Eine Alternative besteht darin, schrittabhängige Übergangsmatrizen T m zu benutzenund jeweils eine lokale Gleichgewichtsbedingung zu fordern, also

qi T mij= qj T m

jifür alle i, j > E. (4.1.11)

Diese schwächere Gleichwichtsbedingung führt ebenfalls zur Konvergenz gegen die stationäreVerteilung [43].

43


4.1.4 Thermalisierung und Autokorrelation

Aufgrund der endlichen Stichprobengröße führen Realisierungen einer Zufallsvariablen, bei de-nen die Zustandsverteilung noch nicht hinreichend genug gegen die stationäre Verteilung kon-vergierte, zu einem systematischen Fehler bei der Approximation des Erwartungswertes dieserZufallsvariablen. Um diesen zu vermeiden, werden Realisierungen aus dieser als Thermalisie-rungsbereich bezeichneten Phase des Random-Walks wieder verworfen. Die Größe dieses Ther-malisierungsbereichs ist dabei stark abghängig von der Startverteilung. Die mögliche Auswir-kung der Wahl der Startverteilung auf die Realisierungen einer Markov-Kette wird in Abbildung4.1 skizziert.

Abbildung 4.1: Abhängigkeit des Thermalisierungsbereichs von der Startverteilung: Startverteilung 2 zeigteine deutlich langsamere Konvergenz gegen die stationäre Verteilung.

Insbesondere ist es bei bestimmter Wahl der Startverteilung möglich, dass die Zustandsvertei-lung der Markov-Kette zunächst gegen eine metastabile Zustandsverteilung konvergiert. Einlängeres Verweilen in Zuständen mit geringem Gewicht bevor die Zustandsverteilung gegen diestationäre Verteilung konvergiert, führt zu einem systematischen Fehler bei der Approxima-tion des zu berechnenden Erwartungswertes. Daher sollten mehere Startverteilungen getestetwerden, um systematische Fehler resultierend aus Ergodizitätsproblemen, wie sie in der An-fangsphase des in Abbildung 4.2 dargestellten Beispiels auftreten, zu vermeiden.Mit zunehmender Länge der Markov-Kette wird natürlich der Einfluss der Nichtgleichgewichts-daten geringer. Dies geschieht mit 1~N , wenn N die Anzahl der Realisierungen ist. Somit wirdder systematische Fehler durch die Thermalisierung bei einer hinreichend langen Markov-Kettekleiner als der statistische Fehler, der wie 1~ºN abfällt. Der Grund, warum jedoch der Therma-lisierungsbereich verworfen werden sollte, liegt in dem oft großen Vorfaktor von 1~N begründet.Um abzuschätzen wie groß der zu verwerfende Thermalisierungsbereich ist, bietet sich die Ana-lyse der so genannten integrierten Autokorrelationszeit an, die in dieser Arbeit im Rahmender Autokorrelation der Markov-Kette eingeführt wird. Der zu verwerfende Bereich sollte danndeutlich größer sein als die aus selbstkonsistenten Messungen stammende integrierte Autokor-relationszeit der Markov-Kette. Allerdings ist die Bestimmung der Autokorrelationszeit rechtaufwendig.

44


Abbildung 4.2: Besuchte Diagrammordnungen k des in Abschnitt 4.2 vorgestellten wcCT-QMC-Algorithmusfür ein 2 2-Hubbard-Cluster mit U = 3.5 und β = 10. Es zeigt sich, dass in den ersten10000 Schritten auf der Markov-Kette die Zustandsverteilung in einem metastabilen Gebietfesthängt. Daher muss entweder die Startverteilung anders gewählt oder entsprechend langegewartet werden bis eine hinreichend gute Konvergenz gegen die stationäre Verteilung vorliegt.

Wurde der systematische Fehler resultierend aus der Thermalisierung eliminiert, stellt sich dieFrage, wie groß der statistsche Fehler der Approximation (4.1.7) ist. Dazu wird im Folgendendavon ausgegangen, dass die Zustandsverteilung sich bereits im Gleichgewicht befindet.

Für unabhängig identisch verteilte Zufallsvariablen ist die Standardabweichung σO der Rea-lisierungen der Zufallsvariablen Oi = OXi von ihrem Erwartungswert gegeben durch die Qua-dratwurzel ihrer Varianz gegeben, also

σO =»

V ar Oi =»` Oi − Òie2 e ∀ i.

Damit erhält man für die Standardabweichung σONdes Mittelwerts ON einer unkorrelierten

Stichprobe Oi, . . . ,ON von seinem Erwartungswert ` ON e:σON

=σOºN

(4.1.12)

Nun sind die einzelnen Realisierungen der Markov-Kette nach Gleichung (4.1.3) offensichtlichnicht stochastisch unabhängig. Eine Fehlerabschäzung nach (4.1.12) ist somit nicht mehr zuläs-sig und würde zu einer Unterschätzung des Fehlers führen. Um ein Maß der Korrelation zweierRealisierungen einzuführen, wird zunächst die Autokovarianz

CovOi − j = Cov Oi,Oj = Òi − ÒeOj − Òee = Òi Oje − Òe2

definiert. Dabei lässt sich offensichtlich die Varianz von Ot als Spezialfall der Autokovarianzfür zwei Realisierungen einer Zufallsvariablen zum gleichen Zeitpunkt auf der Markov-Ketteauffassen:

CovO0 = Cov Ot,Ot = aO2t f − Òe2 = V ar Ot .

Mit Hilfe der Autokovarianz wird nun die normierte Autokorrelationsfunktion k-ter Ordnung

ρOk = CovOkV arOt (4.1.13)

45


definiert. Man beachte, dass durch die Translationsinvarianz einer stationären Markov-Kette dieKorrelation zweier Realisierungen lediglich von ihrem Abstand k = Si− jS auf der Markov-Ketteabhängt.Typischerweise klingt die Autokorrelationsfunktion ρOk asymptotisch für große Abständek ª exponentiell ab:

ρOk exp−k~τexp für k ª,

wobei τexp als exponentielle Autokorrelationszeit bezüglich der Observablen O bezeichnet wird.Durch dieses starke Abfallen der Autokorrelationsfunktion lässt sich eine quasi-unkorrelierteStichprobe erzeugen, wenn der Abstand k zwischen zwei Messungen groß ist gegenüber der ex-ponentiellen Autokorrelationzeit τexp. Für die exponentielle Autokorrelationszeit kann jedochkeine Relation mit dem statistschen Fehler gefunden werden, was allerdings wünschenswertwäre. Um eine Verknüpfung zum statistischen Fehler herstellen, wird die integrierte Autokorre-lationszeit

τint =12

ª

Qk=−ª

ρOk = 12+

ª

Qk=1

ρOk (4.1.14)

definiert. Der Faktor 1~2 ist lediglich per Konvention vorhanden damit die integrierte Auto-korrelationszeit eine Approximation für die exponentielle Autokorrelationszeit darstellt: Wirdangenommen, dass die Autokorrelationsfunktion gemäß ρOk = exp−k~τexp für große Zeitenk verschwindet, so folgt aus (4.1.14) für sehr große exponentielle Autokorrelationszeiten:

τint =12+

ª

Qk=1

e−kτ−1exp =12+

e−kτ−1exp

1 − e−kτ−1exp

12+

1 − τ−1exp

τ−1exp=

12+ τexp − 1

τexp .

Da nur Realisierungen zur Stichprobenerzeugung betrachtet werden sollten, deren Abstandauf der Markov-Kette größer ist als die integrierte Autokorrelationzeit, kontrolliert diese denstatistischen Fehler der Monte-Carlo-Messungen. So gilt für die Varianz des Stichprobenmittels:

V arON = bON − Òe2g = 1N2

N

Qr,s=1

bOrOs −Or Òe −Os Òe + Òe2g

=1

N2

N

Qr,s=1

ÒrOse − Òe2 = 1N2

N

Qr,s=1

CovOr − s .

(4.1.15)

Hier tritt nun in der Summation der Abstand Sr − sS = 0 N -fach und der Abstand Sr − sS =k mit 1 B k B N − 1 genau 2N − k-mal auf. Damit ergibt sich nun für die Varianz desStichprobenmittelwertes:

V arON = 1N2N CovO0 + 2

N−1

Qk=1

N − kCov

=V arO

N21

2+

N−1

Qk=1

1 − k

N ρOk

V arON~2τint

für N Q 1. (4.1.16)

46


Dieses Ergebnis kann dahingehend interpretiert werden, dass von N durchgeführten Messungennur N~2τint statistisch unabhängig sind. Es ist daher erstrebenswert, die Größe der integrier-ten Autokorrelationszeit so weit wie möglich zu reduzieren. Daher sollten zwei Messungen aufder Markov-Kette weiter auseinander liegen als 2τint.Um in einer Simulation praktisch den Fehler zu schätzen, ist man darauf angewiesen, neben derVarianz Informationen über die Autokorrelation ρO numerisch zu bekommen. Betrachtet mandie N Realisierungen einer Markov-Kette X, so ist ein Schätzer für die Autokorrelationsfunktionk-ter Ordnung gegeben durch:

ρOk = PN−kt=1 Ot −ONOt+k −ONPN−k

t=1 Ot −ON2. (4.1.17)

Auch diese Schätzung selbst hat wieder einen Fehler, den man vernachlässigen muss. Um dieintegrierte Autokorrelationzeit τint zu schätzen, sollte man ρOk nur soweit summieren, bis esklein ist. Es ist nicht sinnvoll, Beiträge aufzusummieren, die nur noch aus Rauschen bestehen,da sonst die integrierte Autokorrelationszeit und somit der statistische Fehler der Monte-Carlo-Mittelung überschätzt wird [45].

Möchte man die rechenintensive Abschätzung des statistischen Fehlers aus der Analyse desAbfallverhaltens der Autokorrelationsfunktion ρOk vermeiden, liefert das so genannte Bin-ning einen Ausweg. Dabei werden die korrelierten Datensätze in Blöcke, so genannte Bins, derLänge nb eingeteilt und bildet anschließend b = N~nb Mittelwerte Oj,nb

in den einzelnen Bins:

Oj,nb=

1nb

jnb

Qi=1+j−1nb

OXi mit j = 1, . . . ,N~nb. (4.1.18)

Für Bins sehr großer Länge nb Q τint sind die Mittelwerte Oj näherungsweise unkorreliert, dain diesem Fall die Autokorrelationsfunktion nahezu verschwindet. Daher lässt sich auf auf dieFehlerabschätzung unkorrelierter Daten zurückgreifen:

V arON = 1b − 1

V arOb,nb. (4.1.19)

Es zeigt sich, dass der statistische Fehler für kleiner werdende Binlängen stark anwächst undfür größer werdende Binlängen sättigt. Daher sollte der statistische Fehler bei fester Stich-probengröße N für eine Reihe verschiedener Binlängen nb berechnet werden und anschließendgeprüft werden, ob sich der Fehler mit wachsendem nb stabilisiert. Hierbei ist jedoch zu beach-ten, dass mit wachsender Binlänge die Zahl der Bins sinkt und somit die Ungenauigkeit derBestimmung des statistischen Fehlers ansteigt. Damit die Binning-Methode eine gute Schät-zung für den Fehler liefert, sollte die Binlänge nb stets deutlich größer sein als die integrierteAutokorrelationszeit, aber dennoch hinreichen klein genug um viele Bins zu haben:

τint nb N.

Der systematische Fehler dieser Binning-Methode kann allerdings für zu kleine Bins sehr großwerden. Um dennoch die Idee des Binnings fortzuführen, können alternativ zu den einzelnenBins der Länge nb deren Komplementärbins der Länge nb = N − nb in der Mittelung benutzenwerden:

Oj,nb=

1nb

N

Qi=1

OXi −jnb

Qi=1+j−1nb

OXi . (4.1.20)

47


Dieses so genannte Jackknife-Binning ist somit aufgrund der N~nb − 1 mal größeren Bins we-sentlich robuster gegenüber systematischen Fehlern als die herkömmliche Binning-Methode. Derstatistische Fehler wird nach dem Jackknife-Binning durch

V arON = b − 1 V arOb,nb (4.1.21)

abgeschätzt.

48

4.2 Weak-coupling CT-QMC

4.2 Weak-coupling CT-QMCDie erstmals von A.N. Rubstov und A.I. Lichtenstein [48] vorgestellte diagrammatische Quanten-Monte-Carlo-Methode in kontinuierlicher Zeit stellt eine Erweiterung der Ideen von Prokofev etal. [47] für Bosonen auf fermionische Systeme dar. Dabei basiert der Algorithmus auf einer Dia-grammentwicklung der Zustandssumme im Wechselwirkungsterm und der Resummation derDiagramme in Determinanten. Die resultierenden Diagramme, wie z.B. in Abbildung 4.3 zusehen, werden dann als Realisierungen einer Markov-Kette über den Metropolis-Algorithmuserzeugt. Diese weak-coupling Continous Time-Quantum Monte Carlo-Methode, kurz wcCT-QMC, ist anwendbar auf alle lokalen und auch nicht-lokalen zeitabhängigen Wechselwirkungen.

Abbildung 4.3: Ein Beispieldiagramm dritter Ordnung (k = 3) bestehend aus drei Hubbard-VertizesU niτniτ, die durch Linien verbunden sind, die freie Matsubara-Funktionen G0

στi −τjrepräsentieren. Die Spinabhängigkeit wird durch die Lage der Linien berücksichtigt: oben =Spin-Up, unten = Spin-Up. Abb. entnommen aus Ref. [51].

4.2.1 GrundlagenDie grundlegende Idee der wcCT-QMC-Methode ist die Entwicklung der großkanonischen Zu-standssumme in einer diagrammatischen Störungsreihe unter Betrachtung aller geschlossenen,nicht notwendigerweise zusammenhängender Diagramme:

ΞΞ0

= ` Sβ,0 e0 =ª

Qk=0

−1kk! S

β

0dτ1...dτk `T H1τ1...H1τke0

=

ª

Qk=0

−1k2kk! oτ1α1β1γ1δ1

...oτkαkβkγkδk

Uα1β1γ1δ1 ...Uαkβkγkδkċ

ċ bT c†α1τ1c†

β1τ1cγ1τ1cδ1τ1...c†

αkτkc†

βkτkcγk

τkcδkτkg

0. (4.2.1)

Anzumerken ist bei dieser Entwicklung, dass hier sämtliche Operatoren im modifizierten Dirac-Bild definiert sind. Durch die Allgemeinheit der Entwicklung (4.2.1) lassen sich beliebige Wech-selwirkungen betrachten, wodurch der hieraus abzuleitende Algorithmus auch nicht-lokale Wech-selwirkungen behandeln kann.Um den k-ten Beitrag zu der Zustandssumme durch Diagramme k-ter Ordnung graphisch dar-zustellen, muss der freie Erwartungswert in (4.2.1) mit Hilfe des in Abschnitt 2.5 vorgestelltenWick-Theorems ausgewertet werden. Jeder Summand der totalen Paarung entspricht dann ei-nem bestimmten Diagramm, wobei es 2k! Diagramme k-ter Ordnung gibt. Abbildung 4.3

49


zeigt als Beispiel eins der 720 möglichen Diagramme dritter Ordnung.

Da das permutierte k-Tupel der Indizes den gleichen Beitrag liefert, bietet es sich an, eineKonfiguration bestehend aus den Vertizes τi;αi, βi, γi, δi mit i > 1, ..., k durch

Ck = τ1;α1, β1, γ1, δ1, ..., τk;αk, βk, γk, δk (4.2.2)

zu definieren. Die Zahl der Permuatationen beträgt k!, wodurch sich der Faktor 1~k! in (4.2.1)aufhebt, wenn über den Konfigurationsraum summiert wird. Des Weiteren sind die τi-Integration-en in L = β

∆τbeliebig kleine Zeitschritte zu diskretisieren, um später formal die Metropolisvor-

schlagswahrscheinlichkeiten für das Auswählen einer Zeit abzuleiten, da eine bestimmte Zeit auseinem (kontinuierlichen) Intervall auszuwählen, eine verschwindende Wahrscheinlichkeit besitzt.Allerdings wird die Zeitdiskretisierung bei der Herleitung der Metropolisakzeptanzwahrschein-lichkeiten herausfallen, so dass tatsächlich ein Algorithmus in kontinuierlicher Zeit realisierbarist. Auf die Vorschlags- und Akzeptanzwahrscheinlichkeiten soll jedoch erst in der detailliertenDiskussion des Algorithmus für das Hubbard-Modell eingegangen werden.

Die einzelnen von der Konfiguration Ck abhängigen Summanden sind gegeben durch:

ζCk= −1

2∆τ

k

Uα1β1γ1δ1 ...UαkβkγkδkdetDCk, (4.2.3)

wobei sich die Determinante

detDCk = bT c†α1τ1c†


αkτkc†

βkτkcγk

τkcδkτkg

0(4.2.4)

über das Wick-Theorem als Summe aller Kontraktionen erklärt. Es ist also eine Determinanteeiner k k-Matrix, bestehend aus freien Matsubara-Funktionen. Wie im Abschnitt 4.2.2 fürdas Hubbard-Modell gezeigt wird, zerfällt die Matrix DCk in ein Produkt einer Spin-Up-Matrix DCk mit einer Spin-Down-Matrix DCk. Als Konsequenz faktorisiert auch dieDeterminante (4.2.4):

detDCk = det DCk ċDCk =Mσ

detDσCk. (4.2.5)

Durch Einführung der Verteilung der Konfigurationen ζCklässt sich die Zustandssumme kom-

pakt schreiben alsΞΞ0= Q

k,Ck

ζCk. (4.2.6)

Auf analoge Weise wie für die Zustandssumme lässt sich auch die Matsubara-Funktion entwi-ckeln:

−Gαβτ =` T Sβ,0 cατc†

β0 0f` T Sβ,0 e0

=Pk,Ck

gαβτ,Ck ζCk

Pk,CkζCk

, (4.2.7)

wobei der Wert der Matsubara-Funktion mit der Konfiguration Ck gegeben ist durch:

− gCkαβ τ =

bT cατc†β0c†

α1τ1c†


αkτkc†

βkτkcγk

τkcδkτkg

0

Lσ detDσCk .

(4.2.8)

50


Wird nunsCk

PCk= ζCk

mit sCk=

ζCk

SζCkS

gesetzt, wobei sCkdas Vorzeichen von ζCk

liefert, lässt sich die Matsubara-Funktion als Quotientder Erwartungswerte des Produktes sċgαβτ und des Vorzeichens s bezüglich einer Wahrschein-lichkeitsverteilung PCk

interpretieren:

−Gαβτ =Pk,Ck

gCkαβ τ ζCk

Pk,CkζCk

=

Pk,CkgCkαβ τ sCk

PCk

Pk,CksCk

PCk

=

`s ċ gαβτeP`seP

(4.2.9)

Die beiden Erwartungswerte können nun mit Hilfe einer Markov-Kette näherungsweise be-stimmt werden. Analog zur Matsubara-Funktion lassen sich auch andere Observablen-Erwartungs-werte, wie zum Beispiel die Doppelbesetzung, durch die mit einem Überstrich gekennzeichnetenMonte-Carlo-Mittelwerte bezüglich der stationären Verteilung PCk

approximieren:

`Oeζ =Pk,Ck

sOCk PCk~Pk,Ck

PCk

Pk,Cks PCk

~Pk,CkPCk

sOs

. (4.2.10)

Die für die Monte Carlo-Mittelung benötigten Änderungen der Konfiguration können durchHinzufügen bzw. Entfernen eines Vertex τi;αiβiγiδi realisiert werden.Allerdings ist ein solches Herangehen für die Zustandssumme nicht möglich, da die zur Ver-teilung PCk

gehörende Normierungskonstante unbekannt ist, und sich bei den Observablen-Erwartungswerten lediglich herausgekürzt hat.

Abbildung 4.4: Beispielhistogramm bezüglich der Diagrammordnung k. Abb. entnommen aus Ref. [48].

Es wäre zwar denkbar die Verteilung bezüglich der Störungsordnung k durch Messung des Hi-stogramms (Abbildung 4.4) zu erhalten, aber da der statistische Fehler bei Ordnungen mitgeringem Gewicht groß ist und die ganze Verteilung gerade an einer solchen Stelle bei k = 0 aufEins normiert werden muss, ist dieses Verfahren zu verwerfen. Im Abschnitt 4.3 soll mit demWang-Landau-Algorithmus eine Möglichkeit detailliert diskutiert werden, die Zustandssummeund mit ihr auch das großkanonische Potential stochastisch zu bestimmen.

Das Vorzeichenproblem

Anhand von (4.2.10) erkennt man, dass die Messung von Observablen problematisch werdenkann für Systeme, die eine nicht immer positive Zustandsverteilung ζCk

besitzen, wie es bei

51


einem Großteil der fermionischen Systeme der Fall ist. Hier treten negative Gewichte als Kon-sequenz des Pauli-Prinzips auf. Dieses so genannte Vorzeichenproblem ist charakteristisch fürfast alle Quanten-Monte-Carlo-Methoden. Durch das Bilden des Betrages der Zustandsvertei-lung wird also versucht, ein fermionisches System durch ein vorzeichenproblemfreies Systemzu simulieren. Bei großen Systemen und tiefen Temperaturen unterscheiden sich die relevan-ten Konfigurationen der beiden Systeme und das mittlere Vorzeichen s wird klein (Abbildung4.5). Der relative statistische Fehler wird dann exponentiell groß und wird vom relativen Feh-

Abbildung 4.5: Logarithmiertes mittleres Vorzeichen ln s der wcCT-QMC-Methode für ein 2 2-Hubbard-Cluster bei U = 4 mit drei Elektronen im System in Abhängigkeit der inversen Temperatur β.Abb. entnommen aus Ref. [48].

ler des Vorzeichens dominiert. Um dies zu sehen, betrachte man nun das mittlere `se Vorzei-chen als Quotient der fermionischen Zustandssumme Ξ = Pk,Ck

ζCkund der Zustandssumme

Ξ′ = Pk,CkSζCkS des vorzeichenproblemfreien Systems der Größe Nc bei der inversen Temperatur

β:`se = Ξ~Ξ′ (2.1.1)

= exp−βNcΩ −Ω′ .Damit ist der relative statistische Fehler bei n Monte-Carlo-Messungen gegeben durch:

∆s

`se ¼s2− s2~ns

=1ºn

º1 − s2

s

expβNcΩ −Ω′ºn

.

Da der relative Fehler exponentiell in Nc und β skaliert, skaliert somit die Zahl der Monte-Carlo-Schritte, um einen bestimmten relativen Fehler zu erreichen, auch exponentiell in Nc undβ. Damit scheint der Vorteil der Monte-Carlo-Methoden für große Systeme bei tiefen Tempe-raturen zu verschwinden.Um die entscheidende Idee für die Umgehung des Vorzeichenproblems zu verstehen, betrach-te man nochmals die in (4.2.3) gegebene Verteilung der Konfigurationen. Es ist offensichtlich,dass für attraktive Wechselwirkungen kein Vorzeichenproblem auftritt, sofern die DeteminantedetDσCk für beide Spineinstellungen das gleiche Vorzeichen liefert. Für repulsive Wechsel-wirkungen wird hingegen das Vorzeichen der Verteilung mit der Veränderung der Ordnung kfluktuieren. Dementsprechend muss die repulsive zu einer attraktiven Wechselwirkung trans-formiert werden, um das Vorzeichenproblem zu umgehen. Dies kann innerhalb des CT-QMC-Algorithmus durch geschicktes Hinzufügen einer Konstanten δ geschehen. Allerdings wird dasVorzeichenproblem nur für wenige Systeme, wie z.B. eine Impurity oder eine Hubbard-Kette,komplett auf diese Weise gelöst. Komplexere Systeme, wie allein schon eine Hubbard-Kette

52


mit Übernachstnachbarhopping, wird das Vorzeichenproblem aufweisen. Dennoch lindert dieserAnsatz, der im Abschnitt 4.2.2 in Bezug auf das Hubbard-Modell detailliert diskutiert wird, dieAuswirkung des Vorzeichenproblems für solche Systeme.

Beobachtungen haben gezeigt, dass die Anwesenheit von zusätzlichen Badplätzen das Vorzei-chenproblem mildert. Im Gegensatz zu der exakten Diagonalisierung gibt es im wcCT-QMC-Algorithmus keine Performanceverschlechterung durch deren Hinzunahme. Es werden lediglichkorrelierte Plätze explizit in die Simulation miteinbezogen. Die Badplätze gehen in die Rech-nungen nur durch die als Input benötigte freie Matsubara-Funktion mit ein.

Es ist bekannt, dass es ziemlich sicher keine generelle Lösung für das Vorzeichenproblem gibt,da die Existenz einer Lösung zur Folge hätte, dass alle Probleme der nicht-deterministischenpolynomialen Komplexitätsklasse (NP) in polynomialer Zeit gelöst werden würden [58].

Letztlich beachte man, dass das Vorzeichenproblem des wcCT-QMC-Algorithmus nicht beiSystemen mit Teilchen-Loch-Symmetrie auftritt. Hier haben die ungeraden Diagrammordnun-gen kein Gewicht, so dass zur Erhaltung der Ergodizität die Übergänge durch Hinzufügen bzw.Entfernen zweier Vertizes realisiert werden müssen.

Konvergenz der Reihenentwicklung der Zustandssumme

Bei der sich stellenden Frage nach der Konvergenz der diagrammatischen Entwicklung derZustandssumme in (4.2.1), ergibt sich für für ein endliches fermionisches System eine einfachnachvollziehbare Antwort:Endliche fermionische Vieleilchen-Hamiltonians haben eine endliche Zahl an Eigenszuständen,die 2M beträgt. Dabei ist M die Gesamtzahl der elektronischen Spin-Orbitale in dem System.Nun ist ζCk

< const ċ Wmaxk, wobei Wmax der Eigenwert vom Wechselwirkungsanteils H1 desHamiltonians mit dem größten Beitrag ist. Dies liefert die Konvergenz der Reihenentwicklungder Zustandssumme Ξ, da der Nenner von (4.2.1) wie k! wächst und damit auch schneller wächstals der Zähler, der sich wie Wmaxk verhält.Außerdem ergibt sich die Konvergenz, wenn die mittlere Ordnung `ke endlich bleibt, da dasGewicht sich in bestimmten Ordnungen konzentriert (vgl. Abbildung 4.4). Dabei hängt siebei einer nicht explizit von der Zeit abhängigen Wechselwirkung lediglich von der inversenTemperatur β und dem Erwartungswertes des Wechselwirkungsterms `H1e ab:

`ke = −β `H1e (4.2.11)

und liefert einen Eindruck, welche Ordnungen den größten Beitrag zur Störungsreihe liefern.Ein Beweis dieser Relation ist im Anhang B.2 zu finden.Der Erwartungswert des Wechselwirkungsterms des Hamiltonians ist bei der Hubbard-Wechsel-wirkung im Wesentlichen die erwartete Doppelbesetzung des Systems. Somit ist die mittlereOrdnung mit einer physikalischen Größe verknüpft. Diese ist eine temperatur- und wechsel-wirkungsabhängige Größe, an der auch Phasenübergänge, wie der Mottsche Metall-Isolator-Übergang nachvollzogen werden können. Daher wird die mittlere Ordnung in den verschiedenenPhasen unterschiedlich in der Temperatur und der Wechselwirkungsstärke skalieren. Abbildung4.6 zeigt das unterschiedliche Verhalten der mittleren Ordnung mit der Wechselwirkungstärkebei Behandlung eines metallischen (U < 5) Systems und eines Isolators (U A 5).Da allerdings die Störungsordnungen rein positiv sind und daher auch die mittlere Ordnung,entnimmt man der Relation (4.2.11) ein Problem: Ist der Erwartungswert des Wechselwirkungs-terms positiv, so führt (4.2.11) zu einer negativen mittleren Ordnung. Für solche Systeme tritt

53


Abbildung 4.6: Mittlere Diagrammordnung `ke in Ahängigkeit der Wechselwirkungsstärke U bei DMFT-Rechnungen bei β = 30. Es zeigt sich, dass sich das Verhalten in dem metallischen Bereich(U < 5) von dem im Isolator (U A 5) unterscheidet. Abb. entnommen aus Ref. [51].

gerade das im vorhergehenden Abschnitt 4.2.1 erläuterte Vorzeichenproblem auf. Um das Vor-zeichenproblem zu umgehen, muss also der Wechselwirkungsterm so umformuliert werden, dassder Erwartungswert des Wechselwirkungsterms negativ wird und der Hamiltonian als Ganzesunverändert bleibt. Wie genau man dabei verfahren kann, wird in Abschnitt 4.2.2 anhand desHubbard-Modells im Detail diskutiert.Neben der mittleren Ordnung ist auch die Breite der Verteilung, die durch die Varianz ∆2kcharakterisiert wird, mit dem Erwartungswert des Wechselwirkungsterms verknüpft:

∆2k = −βU∂ `H1e

∂U. (4.2.12)

Für die Herleitung dieser Relation sei auf den Anhang B.3 verwiesen. Bei fester Füllung undfester inverser Temperatur des Systems bestimmt also das Verhalten der Doppelbesetzung so-wohl die mittlere Ordnung als auch die Varianz der Verteilung der Ordnungen. Zusammen-fassend lässt sich anhand der Relationen (4.2.11) und (4.2.12) feststellen, dass diese beidendie Verteilung der Ordnungen charakterisierenden Größen mit der inversen Temperatur β, derWechselwirkungsstärke U und der Systemgröße N anwachsen. Da aber gerade die jeweiligeStörungsordnung die Größe der Matrix Dσ widerspiegelt, ist es offensichtlich, dass der Rechen-aufwand des wcCT-QMC-Algorithmus stark mit diesen Systemparametern ansteigt.

Vergleich mit dem Hirsch-Fye-Algorithmus

Weit verbreitet ist bislang noch der Hirsch-Fye-Algorithmus (HF-QMC) als Cluster-Solver.Die Grundidee dieses Algorithmus ist Diskretisierung der imaginären Zeit τ in Ltrot = β~∆τZeitintervalle. Dadurch kommt man mit der Campbell-Baker-Hausdorff-Formel zu der Trotter-Zerlegung der Zustandssumme:

Ξ = tr e−βH= tr

Ltrot

Ml=1

e−∆τ H tr

Ltrot

Ml=1

e−∆τ H0 e−∆τ H1 .

Diese Approximation führt allerdings auf einen systematischen Fehler, da die Zerlegung nur imGrenzfall ∆τ 0 exakt wird. Da jedoch der Rechenaufwand dieser Methode stark mit kleinerwerdenden ∆τ ansteigt, ist in der Praxis der systematische Fehler nicht vernachlässigbar klein.

54


Um diesen systematischen Fehler zu minimieren, wird der Algorithmus für verschiedene kleineWerte für den Zeitschritt ∆τ durchlaufen. Die erhaltenen Ergebnisse werden dann anschlie-ßend gegen ∆τ 0 extrapoliert. Dadurch erhöht sich jedoch der Rechenaufwand der Methodeund es verbleibt eine Unsicherheit der Extrapolation. Somit zeigt sich hier bereits ein Vorteildes wcCT-QMC-Algorithmus, der auf einer Entwicklung der Zustandssumme Ξ bezüglich derWechselwirkung beruht und damit die imaginäre Zeit τ kontinuierlich bleibt.Weiterhin wird im Hirsch-Fye-Algorithmus eine diskrete Hubbard-Stratonovich-Transformationdurchgeführt um die fermionische Freiheitsgrade zu entkoppeln. Das Vielelektronenproblemwird dadurch auf die Bewegung freier Elektronen in einem zeitunabhängigen Hubbard-Stratono-vich-Feld reduziert. Die Monte-Carlo-Simulation wird dann im Raum der Hubbard-Stratonovich-Felder durchgeführt. Der Algorithmus wurde ursprünglich für lokale Wechselwirkungen konze-piert. Für nicht-lokale und vor allem zeitabhängige Wechselwirkungen wird der Algorithmusineffektiv [48].Da beide Algorithmen auf der Auswertung von Determinanten von Matrizen beruhen, lässt sichderen Performance auch über die jeweilige Matrixgröße vergleichen. Während im Hirsch-Fye-Algorithmus die Matrixgröße durch die Zeitdiskretisierung ∆τ bestimmt ist, ist die Matrixgrößeim CT-QMC-Algorithmus abhängig von der aktuellen Diagrammordnung k. Im Wesentlichentreten dabei nach der Thermalisierung nur Ordnungen nahe der mittleren Ordnung auf.

Abbildung 4.7: Mittlere Matrixgrößen der beiden vorgestellten Algorithmen in Abhängigkeit der inversenTemperatur β bei Berechnung einer Impurity bei U = 4. Abb. entnommen aus Ref. [51].

Bei Betrachtung von Abbildung 4.7 fällt für beide Algorithmen ein lineares Verhalten der Ma-trixgröße mit der inversen Temperatur β auf. Hierbei wurde für den Hirsch-Fye-Algorithmus∆τ = 1~U gewählt. Obwohl die Zeitdiskretisierung um einen Faktor fünf kleiner sein müsste, umden systematischen Fehler durch die Zeitdiskretisierung so zu minimieren, dass die Ergebnisseeine ähnliche Genauigkeit wie die des CT-QMC-Algorithmus aufweisen [51], zeigte sich bereits,dass der Hirsch-Fye-Algorithmus als Impurity-Solver ungefähr dreimal größere Matrizen auszu-werten hat. Auch wenn durch Extrapolation der Ergebnisse des Hirsch-Fye-Algorithmus gegen∆τ = 0 der systematische Fehler durch die Zeitdiskretisierung drastisch verringert werden kann,ist der Algorithmus vermutlich um mehr als einen Faktor zehn langsamer als der CT-QMC-Algorithmus bei gleicher Genauigkeit.

An dieser Stelle sei noch anzumerken, dass es noch eine weitere CT-QMC-Variante gibt, dieauf der diagrammatischen Entwicklung der Zustandssumme in der Hoppingamplitude beruht.Durch diese strong-coupling Entwicklung, daher kommt der Name scCT-QMC, sind die Ma-trizen, deren Determinanten für die Akzeptanzwahrscheinlichkeiten berechnet werden müssen,

55


für starke Wechselwirkungen wesentlich kleiner als die im wcCT-QMC-Algorithmus. Bei einerImpurity führt dies zu einem deutlichen Performancevorteil gegenüber wcCT-QMC. Allerdingsist bei der Clustererweiterung der Methode zunächst der nackte Cluster exakt zu diagonalisie-ren und anschließend der Einfluss der Badplätze auf den Cluster zu simulieren. Damit ist auchdiese Methode auf kleine Cluster beschränkt [89].

56


4.2.2 Detaillierte Beschreibung für das Hubbard-ModellIn diesem Abschnitt soll nun vorgestellt werden, wie die wcCT-QMC-Methode als Solver fürHubbard-Cluster formuliert werden kann. Dazu betrachte man zunächst den Hubbard-Hamiltonian(2.2.6) und schreibe den Wechselwirkungsanteil in symmetrischer Form, also

H = Qi,j,σ

tij c†iσcjσ +UQ

i

ni ni

= Qi,j,σ

tij + U

2δij c†

iσcjσ +UQi

ni −12ni −

12 −Nc

U

4. (4.2.13)

Somit folgt für die diagrammatische Entwicklung der großkanonischen Zustandssumme mit demgroßkanonischen Hamiltonian H =H −Pi µni nach (4.2.1):

e−βNcU~4 ΞΞ0= 1 +

ª

Qk=1

1k!−U

2

k

oτ1,i1

...oτk,ik

` Tk

Mm=1

Mσ

nimστm − 1~2 e0 . (4.2.14)

Die Auswertung des Erwartungswertes in (4.2.14) erfolgt mit dem Wick-Theorem. Dabei liefernKontraktionen mit entgegengesetzten Spins σ keinen Beitrag, also ` c†

c e0 = 0 und der Er-

wartungswert in (4.2.19) zerfällt in ein Produkt zweier Erwartungswerte mit entgegengesetztemSpin:

` Tk

Mm=1

Mσ

nimστm − 1~2 e0 =Mσ

` Tk

Mm=1

nimστm − 1~2 e0 .

Weiterhin folgt mit dem Wick-Theorem:

` Tk

Mm=1

nimστm − 1~2 e0 =QP

signP ċk

Ml=1

c T c†ilστlciPlστPl e0 −

12δl,Pl .

Dies entspricht offensichtlich der Leibniz-Entwicklung einer Determinanten, wobei P eine Per-mutation der Indizes und

signP =¢¦¤

1 für gerade Permutation P,

−1 für ungerade Permutation P

das Vorzeichen der Permutation angibt. Damit stellt der Erwartungswert in (4.2.14) ein Produktzweier Determinanten von der Konfiguration Ck = τ1, i1, ..., τk, ik abhängiger Matrizenmit entgegengesetzten Spin dar:

` Tk

Mm=1

Mσ

nimστm − 1~2 e0 = Mσ

detbT c†ip,στpciq,στqg

0−

12δpq

pq>1,...,k= detDCk ċ detDCk. (4.2.15)

Dies ist gerade das Determinanten-Produkt aus (4.2.5). Um zu sehen, dass die Matrizen Dσ ausfreien Matsubara-Funktionen bestehen, wird ausgenutzt, dass die fermionischen Erzeuger c†

i mitden dazugehörigen Vernichtern cj antikommutieren, sofern sich die Plätze i und j unterscheiden:c†

i , cj = 0 für i x j. Mit der Definition (2.3.7) der Matsubara-Funktion folgt dann:

bT c†ip,στpciq,στqg

0= − bT ciq,στqc†

ip,στpg0= G0

iqipστq − τp,

57


wobei G0ii τ = 0 !

= G0τ = 0− für τq = τp sei.Die freie Matsubara-Funktion G0 stellt damit den für die Simulation benötigten Input überdas System dar und verbindet die einzelnen Vertizes miteinander. Dadurch ist es möglich, zu-sätzlich zu den korrelierten Plätzen, noch weitere Badplätze hinzuzufügen, ohne die Performanceder Methode zu verschlechtern. Die Badplätze gehen nur über die freie Matsubara-Funktion ein.Die Simulation hingegen findet nur auf den korrelierten Plätzen statt, da nur auf diesen eineWechselwirkung vorhanden ist und somit auch nur diese in die Vertizes aufgenommen werden.Damit ist auch die Simulation eines kontinuierlichen Bades möglich. Wie sich in Abschnitt 4.3zeigen wird, bewirken Badplätze eine kleinere mittlere Ordnung und damit werden im MittelDeterminanten kleinerer Matrizen berechnet. Da diese Berechnung wie k3 skaliert, führen Bad-plätze zu einer Performanceverbesserung.Des Weiteren kann man der Matrix Dσ entnehmen, dass diese wegen den Eigenschaften (2.3.26)und (2.3.25) der Matsubara-Funktion bei Teilchen-Loch-Symmetrie antisymmetrisch wird, wo-durch die Determinante lediglich für gerade Ordnungen k einen Beitrag liefert.

Durch die Einführung der Konfiguration Ck und der Zeitdiskretisierung der τ -Integrationenlässt sich die Zustandssumme schreiben als

ΞΞ0= 1 +

ª

Qk=1

QCk

−U

2∆τ

k

Mσ

detDσCk = 1 +ª

Qk=1

QCk

ζUCk, (4.2.16)

wobei die Verteilung ζU der Konfigurationen Ck durch

ζUCk = −U

2∆τ

k

Mσ

detDσCk (4.2.17)

gegeben ist. Analog findet man für die Matsubara-Funktion

Gii′στ − τ ′ = Pk,CkgCkii′σ τ − τ ′ζUCkPk,Ck

ζUCk ,

wobei der von der Konfiguration Ck abhängige Wert der Matsubara-Funktion gegeben ist durch:

gCkii′σ τ − τ ′ = aT c†

i′στ ′ciστLkm=1nimστm − 1~2f0

detDσCk .

Bei Teilchen-Loch-Symmetrie (µ = U~2) ist ganz sicher detD = detD. Damit sollten intuitivnach (4.2.17) für ungerade Ornungen k negative Monte-Carlo-Gewichte auftreten. Wie weiteroben bereits angemerkt wurde, verschwindet die Determinante der bei Teilchen-Loch-Symmetrieantisymmetrischen Matrix Dσ bei ungeraden Ordnungen, so dass dann stets positive Monte-Carlo-Gewichte vorhanden sind und das Vorzeichenproblem nicht existiert. Das Verschwindender Gewichte ζUCk bei ungeraden Ordnungen führt dazu, dass die Monte-Carlo-Schritte nichtmehr durch Einfügen bzw. Entfernen eines Vertex realisiert werden können. Stattdessen müs-sen die Schritte auf der Markov-Kette durch Übergänge zu der übernächsten Ordnung zustandekommen.Abseits von Halbfüllung (µ x U~2) wird das Vorzeichenproblem im Allgemeinen nicht vermie-den werden können. Allerdings kann auch für null- und eindimensionale Hubbard-Modelle ohneFrustration das Vorzeichenproblem umgangen werden, indem man geschickt eine Konstante

58


Abbildung 4.8: Diagramm dritter Ordnung (k = 3). Jeder Vertex beinhaltet auch ein Ising-Feld si = 1 um dasVorzeichenproblem zu unterdrücken und wird auch in den Metropolis-Updates mitberücksich-tigt. Jeder Vertex wird durch Linien verbunden, die die Matsubara-Funktionen repräsentieren.Dabei steht Rot für Spin-Up und Grün für Spin-Down. Abb. entnommen aus Ref. [49].

hinzuaddiert und anschließend wieder abzieht. Die dadurch bewirkte Polarisation des Systemskann statisch durch eine feste Konstante α [48] oder durch eine Ising-Spin-ähnliche Hilfsgrößesi = 1 für jeden Platz i dynamisch geschehen (αsi) [50], indem jedes Tupel τj ; ij einerKonfiguration Ck um den Eintrag sij erweitert wird, also τj ; ij , sij. Abbildung 4.8 zeigt einBeispieldiagramm dritter Ordnung für das Hubbard-Modell mit einem Ising-Hilfsfeld. Entspre-chend wird für diesen Ansatz die Hubbard-Wechselwirkung aus (4.2.13) geeignet umgeschrieben,so dass

H1 = UQi

ni, − 1~2 ni, − 1~2 =U

2Qi

Qsi=1

ni − 1~2 − siδ ni − 1~2 + siδ +NcUδ2

=U

2Qi

Qsi=1

ni − αsi ni − αsi +NcUδ2

= H1 +NcUδ2

Hierbei ist die dynamische Größe α als

αδσsj = 1

2+ signσ sjδ (4.2.18)

mit beliebigen Parameter δ definiert und es gilt: αδsj + αδ

sj = 1.Im Folgenden wird nur noch das Hubbard-Modell mit der Wechselwirkung H1 betrachtet, dessenZustandssumme nach (4.2.1) gegeben ist durch

ΞΞ0= 1 +

ª

Qk=1

1k!−U

2

k

oτ1,i1,s1

...oτk,ik,sk

` Tk

Mm=1

Mσ

nimστm − αδσsm e0 . (4.2.19)

Die Zustandssumme Ξ für den Original-Hamiltonian ist dann

Ξ = e−βNcUδ2Ξ. (4.2.20)

Auf die Matsubara-Funktion bzw. auf die Observablenerwartungswerte hat das Hinzufügen derKonstanten jedoch keinen Einfluss.Die Wahl des Parameters δ lässt sich aus dem Hubbard-Modell im atomaren Limes Nc = 1ableiten, da dieses analytisch lösbar ist. Der dazugehörige großkanonische Hamiltonian lautet

Hatomar= −µn +Un − 1~2n − 1~2 −Uδ2,

59


woraus zusammen mit der Fugazität z = eβµ die folgende großkanonische Zustandssumme folgt:

Ξ = e−βU1~4−δ2+ 2zeβU1~4+δ2

+ z2e−βU1~4−δ2. (4.2.21)

Wird nun die Zustandssumme in Analogie zur Diagrammentwicklung (4.2.19) nach der Wech-selwirkungsstärke U entwickelt, ergibt sich:

Ξ =ª

Qk=0

Uk βk

k!δ2

− 1~4k + 2zδ2+ 1~4k + z2δ2

− 1~4k . (4.2.22)

Anhand dieser Reihendarstellung zeigt sich wieder, dass bei Teilchen-Loch-Symmetrie, die indiesem Fall bei µ = 0 eintritt4 und z = 1 zur Folge hat, ungerade Ordnungen verschwinden undsomit das Vorzeichenproblem nicht auftritt. Abseits von Halbfüllung muss δ jedoch so gewähltwerden, dass die Summanden von (4.2.22) stets positiv sind. Dies ist offensicht für δ A 1~2 derFall und damit bleiben auch die Gewichte (4.2.17) positiv.5

Da allerdings die mittlere Ordnung nach Gleichung (4.2.11) mit δ anwächst, also

` k e = −βU ` d e − 12` n e + 1

4− δ2 , (4.2.23)

wobei ` n e die erwartete Besetzung und ` d e = ` nn e die erwartete Doppelbesetzung ist, unddie mittlere Ordnung gerade der mittleren Größe der Matrizen DσCk entspricht, deren Deter-minanten für die Akzeptanzwahrscheinlichkeiten des Metropolis-Algorithmus bestimmt werdenmüssen, sollte δ wiederum möglichst klein gewählt werden, damit eine optimale Performanceerreicht wird. Damit ist die optimale Wahl des Parameters δ für das Hubbard-Modell abseitsvon Halbfüllung gegeben durch:

δ =12+ 0+ . (4.2.24)

Für diese Wahl tritt somit das Vorzeichenproblem für das Hubbard-Modell im atomaren Limesnicht auf. Auch für die Hubbard-Kette ohne Frustration existiert das Vorzeichenproblem beidieser Wahl nicht [50]. Für komplexere Hubbard-Modelle, wie zum Beispiel ein Hubbard-Ringoder ein Hubbard-Modell in höheren Dimesionen kann das Vorzeichenproblem abseits von Halb-füllung nicht umgangen werden. Es zeigt sich jedoch, dass das Vorzeichproblem bei dieser Wahlgemildert wird.Liegt allerdings Teilchen-Loch-Symmetrie vor, so ist auf jeden Fall die Methode mit Übergängenzu den übernächsten Ordnungen und δ = 0 zu wählen, da damit eine bessere Performance zuerzielen ist. Der Parameter δ führt schließlich bei einem Nc-Platz-Hubbard-Model zu einer Ver-schiebung der mittleren Ordnung um βUNcδ

2 zu größeren Ordnungen. Um dennoch Übergängezu benachbarten Ordnungen zu realisieren, obwohl ungerade Ordnungen ein verschwindendesGewicht besitzen, sollte δ auf einen kleinen Wert gesetzt werden. Durch die so entstehende Pola-risation des Systems haben auch ungerade Ordnungen ein nicht-verschwindendes Gewicht. Manbeachte, dass hier eine Wahl von δ lediglich zur Abänderung der Übergangwahrscheinlichkeitenbenötigt wird. Ein Vorzeichenproblem existiert bei teilchen-loch-symmetrischen Systemen nicht.

Für die Monte-Carlo-Simulation mit dem Ising-Hilfsfeld über den Metropolis-Algorithmus wird

4Man beachte, dass sich das herkömmliche Hubbard-Modell im atomaren Limes mit Halbfüllung bei U~2lediglich durch Addition von U~2 ergibt; vgl. Gleichung (4.2.13) .

5Sicherlich sind bei sehr hohen Temperaturen auch kleinere Werte für δ möglich, um das Vorzeichenproblemzu umgehen. Wird z.B. der Term erster Ordnung in (4.2.22) analysiert, so bleibt dieser positiv für δ A 1

2z−1z+1

.

60


die unnormierte Verteilung der Konfigurationen

ζUCk = −U

2∆τ

k

Mσ

detDσCk = −U

2∆τ

k

Mσ

det G0iqipστq − τp − δpqαδσsp

(4.2.25)als Wahrscheinlichkeit interpretiert.Die für den Algorithmus benötigten Zuständsänderungen werden entweder durch Hinzufügeneines Vertex

Ck Ck+1 = τ1, i1, s1, ..., τk, ik, sk, τk+1, ik+1, sk+1oder durch Entfernen eines Vertex

Ck Ck−1 = τ1, i1, s1, ..,XXXXXτj , ij , sj, ..., τk, ik, sk

realisiert. Intuitiv bietet sich für die Vorschlagswahrscheinlichkeit für das Hinzufügen einesVertex

MCkCk+1 =1

2NcL=

∆τ

2Ncβ(4.2.26)

an, da es 2 mögliche Werte für s, Nc für i und nach der zu Beginn angesprochenen Zeitdiskre-tisierung L = β~∆τ

∆τ0Ð ª mögliche Werte für τ gibt und somit 2NcL gleichwahrscheinliche

Möglichkeiten einen Vertex einzufügen existieren.Unter der Annahme, dass das Entfernen eines von k Vertizes einer Gleichverteilung gehorcht,folgt für die Vorschlagswahrscheinlichkeit um einen Vertex zu entfernen:

MCkCk−1 =1k

. (4.2.27)

Es ist offensichtlich, dass diese Wahl für die Referenzkette, die die Zustandswechsel vorschlägt,dazu führt, dass aus jeder beliebigen Konfiguration jede andere erreichbar ist und die Refe-renzkette irreduzibel ist. Außerdem tritt bei dieser Wahl der Vorschlagswahrscheinlichkeitenkeine Periodiztät bei den Zustandswechseln auf, so dass auch die Aperiodizität gewährleistet istund somit die Zustandsverteilung im Metropolis-Algorithmus gegen die gewünschte stationäreVerteilung ζUCk~Pk,Ck

ζUCk konvergiert.Die für die Anwendung des Metropolis-Algorithmus benötigten Akzeptanzwahrscheinlichkeitenfür das Hinzufügen bzw. für das Entfernen eines Vertex ergeben sich nach Gleichung (4.1.10)zu:

ACkCk+1 = min−UNcβ

k + 1Lσ detDσCk+1Lσ detDσCk ,1 (4.2.28)

ACkCk−1 = min− k

UNcβ

Lσ detDσCk−1Lσ detDσCk ,1 . (4.2.29)

Wird nach einigen Autokorrelationszeiten eine quasi-unkorrelierte Konfiguration erreicht, sowird die gewünschte Observable gemessen. Dabei ist zum Beispiel der Wert der Matsubara-Funktion bei einer gegebenen Konfiguration gegeben durch


i′στ ′ciστLkm=0nimστm − αδ

σsmf0

detDσCk .

61


4.2.3 Update-Formeln und Messung von Erwartungswerten

Bei der Berechnung der Akzeptanzwahrscheinlichkeiten treten also Brüche von Determinantenauf. Deren Berechnungszeit skaliert typischerweise mit k3. Aus der Sherman-Morrison-Formellassen sich Update-Formeln finden, durch die sich der Rechenaufwand deutlich verringert, sodass die Berechnungszeit der Akeptanzwahrscheinlichkeiten nur noch mit k2 skaliert.

Zunächst betrachte man das Entfernen eines Vertex. Die Berechnung des Bruchs der zwei Deter-minanten in der entsprechenden Akzeptanzwahrscheinlichkeit (4.2.29) kann auf das Invertierender Matrix Dσ reduziert werden:

detDσCk−1detDσCk =D−1rrσCk. (4.2.30)

Um nicht nach jedem Schritt die Matrix Dσ erneut zu invertieren, kann D−1σ für die jeweils

neue Ordung aktualisiert werden:

D−1pqσCk−1 =D−1pqσCk + δprδrq −D−1prσCk 1D−1rrσCkD

−1rqσCk, (4.2.31)

wobei anschließend noch die r-te Zeile und r-te Spalte aus der dazugehörigen Matrix gestrichenwerden müssen.

Beim Hinzufügen eines Vertex vereinfacht sich die Berechnung des Bruchs der Determinan-ten in der Akzeptanzwahrscheinlichkeit (4.2.28) auf:

detDσCk+1detDσCk =Dk+1,k+1,σCk+1 −

k

Qi,j=1

Dk+1,i,σCk+1D−1i,j,σCkDj,k+1,σCk+1. (4.2.32)

Das Update erfolgt hier etwas komplizierter durch

D−1σ Ck+1 = B +u2v

T2 −1=B−1 −

B−1u2vT2 B−1

1 + vT2 B−1u2

(4.2.33)

mit

B−1 = DσCk +u1vT1 −1=D−1

σ Ck − D−1σ Cku1v

T1 D−1

σ Ck1 + vT

1 D−1σ Cku1

,

uT1 = 0, ...,0,1,

vT1 = Dk+1,1,σCk+1, ...,Dk+1,k+1,σCk+1,

uT2 = D1,k+1σCk+1, ...,Dk,k+1,1σCk+1,−1,

vT2 = 0, ...,0,1.

Die Zustandsänderungen durch Hinzufügen bzw. Entfernen eines Vertex sind für den Algorith-mus völlig ausreichend. Im Fall von Teilchen-Loch-Symmetrie existiert kein Vorzeichenproblemund es sind nur direkte Übergänge zwischen geraden Ordnungen erlaubt, also z.B. k k 2.Eine Diskussion der Update-Formeln für solche Übergänge ist in [48] zu finden.

62


Messung der Matsubara-Funktion und von Observablen

Bei der Messung der Matsubara-Funktion tritt ebenfalls ein Bruch zweier Determinanten auf:


i′στ ′ciστLkm=1nimστm − αδ

σsmf0

detDσCk=

detA

detDσCk ,

wobei

A =

G0ii1στ − τ1

DσCk

G0iikστ − τk

G0i1i′στ1 − τ ′ G

0iki′στk − τ ′ G

0ii′στ − τ ′

.

Dieser Ausdruck für den Wert der Matsubara-Funktion bei der Konfiguration Ck lässt sichsomit mit Hilfe der Sherman-Morrison-Formel analog zu den Metropolis-Updates vereinfachen:

gCkii′σ τ − τ ′ = G

0ii′στ − τ ′ −

k

Qr,s=1

G0iri′στr − τ ′D−1rsσCkG0iisστ − τs. (4.2.34)

Der Übergang in die Frequenzdarstellung erfolgt durch die Fouriertransformation (2.3.10) undergibt nach Anhang B.4:

gCkii′σ iω = G

0ii′σiω − S

β

0dτ eiωτ

k

Qr,s=1

G0iri′στrD−1rsσCkG0iisστ − τs

= G0ii′σiω −

1β

k

Qr,s=1

G0iri′σiω eiωτsD−1rsσCke−iωτrG0iisσiω.

Dabei ist die erste Darstellung ist besser geeignet für die Implementierung als die zweite, dadort nur ein Fourierfaktor eiωτ vorhanden ist und somit die Gefahr von numerischen Ungenau-igkeiten kleiner ist. Zur praktischen Berechnung wird die Zeitintegration noch diskretisiert.

Nicht nur Matsubara-Funktionen lassen sich mit dem Algorithmus messen, sondern beliebigeObservablenerwartungswerte. Dabei wird der Wert der Observablen O bei einer Konfigurati-on Ck analog zur Matsubara-Funktion bestimmt durch eine Determinante, die sich über dasWick-Theorem aus einem freien Erwartungswert der Form

dT Ok

Mm=1

nimστm − αδσsmi

0

ergibt, wobei O der entsprechende Operator der zu messenden Observablen ist. Damit ergibtsich der Wert einer Observablen O bei einer Konfiguration Ck aus:

OCk =aT OLk

m=1nimστm − αδσsmf0

detDσCk . (4.2.35)

Da dies wieder einem Bruch zweier Determinanten entspricht, lässt sich wieder analog zurMatsubara-Funktion die Sherman-Morrison-Formel verwenden.

63


4.3 Der Wang-Landau-Algorithmus als VCA-Cluster-SolverDer in den vorhergehenden Abschnitten vorgestellte Metropolis-Algorithmus hat eine großeSchwäche: Während sich die Observablenerwartungswerte bestimmen lassen, ist die großka-nonische Zustandssumme Ξ, die zur Berechnung des für den Variational Cluster Approxima-tion benötigten großkanonischen Potentials Ω′ eines Clusters (siehe Gleichung (3.2.2)), nichtzugänglich. Der Random-Walk enthält aber dennoch die für die Zustandssumme benötigtenInformationen. So erhält man durch das Aufnehmen eines Histogramms, das die Besuche derdiagrammatischen Störungsordnungen zählt (Abbildung 4.4), eine Approximation für die Ver-teilung PCk

ζUCk der Diagrammordnungen. Problematisch ist jedoch die richtige Normierungder Approximation, die notwendig ist, da sich Histogramm und PCk

ζUCk bis auf einen kon-stanten Faktor unterscheiden. Mit „Normierung“ ist hier also nicht gemeint, dass die Summeüber alle Zustände Eins ergibt. Die Normierung der approximativen Verteilung ist möglich,weil PCk

ζUCk für k = 0 bekannt ist. Die nullte Ordnung repräsentiert das freie System, wo-durch also die gesamte Verteilung festgelegt wird. Allerdings ist dies für das Histogramm einesMetropolis-Walks nicht praktikabel, da die nullte Ordnung meist eine sehr schlechte Statistikaufweist und somit die gesamte bestimmte Verteilung eine sehr unsichere Näherung darstellt.F.Wang und D.P. Landau fanden einen alternativen stochastischen Algorithmus [56], mit demsich die Zustandsverteilung bezüglich der diagrammatischen Störungsordnung konstruieren lässt.In diesem Algorithmus weist jede Ordnung eine gleich gute Statistik auf. Dadurch ergibtsich nach Normierung eine gute Approximation der Verteilung der Diagrammordnungen. Eineweitere Stärke des Wang-Landau-Algorithmus ist, dass sich basierend auf dem wcCT-QMC-Algorithmus für das Hubbard-Modell das großkanonische Potential, sowie die Matsubara-Funk-tion und Observablenerwartungswerte, wie beispielsweise die Doppelbesetzung an einem Git-terplatz, für alle Wechselwirkungsstärken U berechnet werden können. Im Folgenden wird derAlgorithmus in Analogie zur Quanten-Monte-Carlo-Methode als wcCT-WL bezeichnet.

Zunächst betrachte man nochmals die Entwicklung der Zustandssumme (4.2.16):

ΞΞ0= 1 +

ª

Qk=1

QCk

−U

2∆τ

k

Mσ

detDσCk = 1 +ª

Qk=1

QCk

ζUCk .

Nun wird eine unnormierte Zustandsverteilung bezüglich der Diagrammordnung k als Summeder Zustandsverteilung ζUCk bezüglich der Konfiguration Ck definiert, die unabhängig vonder Wechselwirkungstärke U ist:

wk = U−k QCk

ζUCk =QCk

ζ1Ck = −∆τ

2

k

QCk

Mσ

detDσCk . (4.3.1)

Damit folgt aus (4.2.16) für die Zustandssumme:

ΞΞ0=

ª

Qk=0

Uk wk mit w0 = 1 . (4.3.2)

Das Ziel des Wang-Landau-Algorithmus ist es, eine für alle Ordnungen gleich gute Verteilungdieser zu bestimmen. Dies wird möglich durch eine Neugewichtung der Zustandsverteilung wkmit einer mit jedem Schritt auf der Markov-Kette zu modifizierenden Funktion 1~gk. Dabeiwird am Ende des Algorithmus die Funktion gk als Approximation für die Verteilung wkdienen.Durch die Neugewichtung ergibt sich nun als Zustandsverteilung für den wcCT-WL-Algorithmus

ζ1Ck = 1gkζ1Ck Ô wk = 1

gk wk. (4.3.3)

64

4.3 Der Wang-Landau-Algorithmus als VCA-Cluster-Solver

Durch Modifikation von gk bei der besuchten Ordnung k mit einer multiplikativen Konstantef A 1, also

gkÐ gk ċ f, (4.3.4)

mit jedem Schritt auf der Markov-Kette, was auch das Bleiben in einer Ordnung beinhaltet,werden die Akzeptanzwahrscheinlichkeiten

AWLCkCk+1

= min−Ncβ

k + 1ζ1Ck+1ζ1Ck

,1 , (4.3.5)

AWLCkCk−1

= min− k

Ncβ

ζ1Ck−1ζ1Ck

,1 (4.3.6)

für einen Metropolis-Walk ständig verändert, wodurch die Übergänge zu Ordnungen k mitgroßem Gewicht immer unwahrscheinlicher werden, bis alle Ordnungen annähernd gleichwahr-scheinlich sind. Infolgedessen ist die Markov-Kette weder homogen noch reversibel. Allerdingswird auch dadurch bis auf eine multiplikative Konstante Λ eine Konvergenz der Verteilung ggegen die unnormierte Zustandsverteilung w erreicht und es gilt dann:

gk = Λ wk für tª . (4.3.7)

Dies bedeutet, dass wenn die Verteilung g hinreichend weit gegen die Zustandsverteilung wkonvergiert ist, ergibt sich

wk = Λ−1 = const. (4.3.8)

und weil wk proportional zu einem während des Ablaufs auf der Markov-Kette aufgenomme-nen Histogramms Hk ist, wird dieses bis auf ein statistisches Rauschen „flach“ werden. DieFlachheit des Histogramms spiegelt die resultierende Gleichverteilung wider und stellt ein Maßfür den Konvergenzfortschritt von g dar.Abbildung 4.9 illustriert das flache Histogramm eines Hubbard-Rings mit vier Plätzen. Man be-achte, dass lediglich die relative Abweichung vom Histogrammmittelwert mit der Monte-Carlo-Zeit geringer wird. Eine statistisch bedingte Rauhigkeit wird in jedem Fall bestehen bleiben.

Die relative Abweichung des Maximalwerts von dem Mittelwert H des Histogramms

Hmax −H

H=

∆H

H

ist ein geeignetes „Flachheits“-Kriterium. Mit der Zeit konvergiert dieses gegen Null. Je kleineralso die an den Algorithmus geforderte relative Abweichung ist, desto besser ist die Approxi-mation von wk durch gk.An dieser Stelle ist anzumerken, dass dieses Verfahren nur für endlich viele Ordnungen effektivmöglich ist, da nicht alle Ordnungen in endlicher Zeit durchlaufen werden können und somitMaximum und Mittelwert der Verteilung effektiv nicht gegeneinander konvergieren. Das Hi-stogramm könnte somit nie „flach“ werden. Da Beiträge sehr großer Ordnungen kaum einenBeitrag leisten, wird ein Cutoff-Wert kc für die Ordnung eingeführt. Die Wahl des Cutoffs musshinreichend groß gewählt werden, sodass der Beitrag aller folgenden Ordnungen vernachlässig-bar klein ist. Mit dem Cutoff kc ergibt sich nun nach N Schritten auf der Markov-Kette unterVoraussetzung einer Gleichverteilung auf dem Intervall der betrachteten Ordnungen 0, kc dasfolgende „Flachheits“-Kriterium:

Hmax −H

H=

kc

NHmax − 1 B η . (4.3.9)

65


Abbildung 4.9: Wang-Landau-Histogramm eines 4-Platz-Hubbard-Rings mit U = 1 bei β = aufgenommen beieinem Modifikationsfaktor f = e und Cutoff-Ordnung kc = 11

Obwohl durch eine immer striktere Auslegung dieses „Flachheits“-Kriteriums die Statistik in-tuitiv verbessert werden sollte, bleibt dennoch ein statistisches Rauschen, das mit der Wahldes Modifikationsfaktors f zusammenhängt, und es kommt zu einer Sättigung des statistischenFehlers der Verteilung g. Daher macht es keinen Sinn sehr kleine Werte für η zu fordern. Soscheint η = 0.2 eine mehr als hinreichende Wahl darzustellen.Je kleiner der Modifikationsfaktor f ist, desto kleiner wird aber auch letztendlich das statis-tische Rauschen und der statistische Fehler sollte sich wie

ºln f verhalten [59]. Daher ist es

eine lohnenswerte Strategie den Modifikationsfaktor f jedes Mal zu verkleinern nachdem dasFlachheits-Kriterium zum Abbruch des Walks führte und dann einen neuen Walk mit einemzurückgesetzten Histogramm zu starten, um eine verfeinerte Annäherung der Gewichte g an dieZustandsverteilung w zu erhalten. Die Verkleinerung des Modifikationsfaktors f erfolgt dabeinach einer monoton fallenden und gegen 1 konvergierenden Folge. F.Wang und D.P. Landau[56] schlugen

fi+1 = f1~ai mit a A 1, f0 A 1 und a, f0 > R, i > N0 (4.3.10)

als eine geeignete Folge für die Verkleinerung des Modifikationsfaktors f vor. Dabei ist zu be-achten, dass sowohl die Wahl von f0 als auch von a einen entscheidenden Einfluss hat. Eserscheint ersichtlich, dass je kleiner f ist, desto mehr Schritte auf der Markov-Kette gebrauchtwerden, um die gewünschte Flachheit zu erreichen. Werden also f0 oder a sehr klein gewählt,wird eine große Berechnungszeit benötigt. Ist allerdings f relativ groß, ist auch der statistischeFehler groß. Das Setzen des Startwertes des Modifikationsfaktors auf f0 = e erlaubt es den ge-samten ausgewählten Zustandsraum relativ schnell zu durchlaufen. In Kombination mit kleinenWerten für a und somit einer langsamen Konvergenz gegen 1 führt dies zu einem effizientenAlgorithmus (vgl. [62],[61]), in dem die Verfeinerung des Modifikationsfaktors f mit jeweils an-schließendem Random-Walk durchgeführt wird, bis f hinreichend weit gegen 1 konvergiert ist,z.B. bis f 1 + 10−8.Um die Effizienz des Algorithmus noch weiter zu erhöhen, bietet sich auch eine andere Wahl fürdie Folge der Modifikationsfaktoren an: Hat der statistische Fehler seine Sättigung erreicht, be-ginnt ∆H~H für ein festes f proportional zur inversen Monte-Carlo-Zeit t−1 kleiner zu werden.Betrachtet man nun die Summe H ′ der Histogramme aller Modifikationsfaktoren, so erkennt

66


man ein lineares Wachstum von sowohl ∆H ′ als auch H ′ mit der Monte-Carlo-Zeit, wenn dieFolge der Modifikationsfaktoren in Abhängigkeit von der Monte-Carlo-Zeit schneller abfällt als1~H ′t, was in dem Wang-Landau-Algorithmus der Fall ist. Somit wird also nicht nur fürein festes f eine Fehlersättigung erreicht, sondern auch für den gesamten Algorithmus. DieseSättigung kann umgangen werden, indem ein Algorithmus gefunden wird, in dem der Modi-fikationsfaktor mit der Monte-Carlo-Zeit langsamer abfällt als 1~H ′t. R.E. Belardinelli undV.D. Pereyra [62] schlugen vor, zunächst mit dem konventionellen Wang-Landau-Algorithmuszu beginnen und die Folge der Modifikationsfaktoren durch einen von der Monte-Carlo-Zeitabhängigen Modifikationsfaktor

ft = e−1~t (4.3.11)

zu ersetzen, wenn fi B ft erreicht wurde. Der Modifikationsfaktor (4.3.11) ändert sich somitmit jedem Schritt auf der Markov-Kette und es wird kein Histogramm oder Flachheits-Kriteriummehr benötigt. Dieser Algorithmus führt zu einer wesentlich besseren Approximation von w, inwelcher der statistische Fehler wie t−1~2 kleiner wird.Für eine schnelle Konvergenz gegen die zu bestimmende Verteilung ist auch noch die Wahl derStartverteilung für gk von Bedeutung. Sind keine Vorkenntnisse über die Verteilung vorhan-den, so werden alle Ordnungen als gleichverteilt angenommen, also gk = 1 ∀k.

Abbildung 4.10: Abhängigkeit der Verteilung der Diagrammordnungen von der Wechselwirkungsstärke Ueines halbgefüllten 2 2-Hubbard-Clusters bei β = 5.

Am Ende der Simulation ist g jedoch nur bis auf einen Faktor Λ gegen w konvergiert. DieserNormierungsfaktor ergibt sich aus der Tatsache, dass der Entwicklungsterm nullter Ordnunggerade der Zustandssumme Ξ0 des freien Systems entsprechen muss und somit w0 = 1 ist.Das heißt wiederum mit 4.3.7, dass der Normierungsfaktor Λ = g0 ist und daher w und damitauch die Zustandssumme (4.2.16) über

ΞΞ0=

ª

Qk=0

Uk wk 1g0

kc

Qk=0

Uk gk (4.3.12)

approximiert werden kann.

67


Die Wahl des Cutoffs ist entscheidend für die Güte der Approximation (4.3.12). Der Cutoffsollte so groß gewählt werden, dass der Beitrag noch größerer Ordnungen vernachlässigbarklein ist. Dadurch liefert die Approximation (4.3.12) die Möglichkeit mit nur einer Simulationdie approximative Verteilung g zu bestimmen, die für alle Wechselwirkungsstärken U gilt. Wieman jedoch Abbildung 4.10, die das Verhalten der Verteilung Ukgk~Λ bei Variation von Uzeigt, entnehmen kann, ist die Approximation der Zustandssumme nur bis zu einem cutoff-bedingten Wert für alle Wechselwirkungsstärken möglich. Wird die approximative Verteilung gfür zu große Wechselwirkungsstärken benutzt, so ist der Beitrag für Ordnungen größer als derCutoff nicht mehr vernachlässigbar und die Approximationsgüte nimmt stark ab.Abbildung 4.11 zeigt eine Beispielverteilung für einen halbgefüllten 2 2-Hubbard-Cluster beiβ = 10 und U = 1. Auffällig ist an dieser ist, dass sie eine Ähnlichkeit zu einer Gauß-Kurvebesitzt und eine leichte Asymmetrie zu größeren Diagrammordnungen aufweist. Dieser stärkerausgeprägte Tail, macht die optimale Wahl des Cutoffs kc schwierig. Da allerdings der Tail ex-ponentiell abfällt, ist eine Wahl des Cutoffs und damit das Vernachlässigen von noch größerenOrdnungen durchaus gerechtfertigt.

Abbildung 4.11: Wahrscheinlichkeitsverteilung pk = wk~Pk wk der Diagrammordnungen im wcCT-QMCeines halbgefüllten 22-Hubbard-Clusters bei β = 10 und U = 1. Die Verteilung weist gegen-über einer symmetrischen Fortsetzung nach ihrem Maximum einen stärkeren Tail zu großenOrdnungen auf.

Eine konservative Abschätzung für den Cutoff ist gegeben dadurch, dass Ordnungen vernach-lässigbar sind, deren Gewicht kleiner als 0.5 % des Maximums der Verteilung gk ist, alsogkc < 0.005 gkmax. Dies sind allerdings insbesondere auch Ordnungen, die auf der linkenFlanke der Verteilung liegen (siehe Abbildung 4.11), sodass neben dem oberen Cutoff ko

c = kc

auch eine Einführung eines unteren Cutoffs kuc sinnvoll ist. Man beachte jedoch, dass für die Zu-

standssumme Ξ~Ξ0 die Verteilung g noch anhand der Ordnung k = 0 zu normieren ist, wodurchder untere Cutoff lediglich nur für Observablenmessungen, die im nächsten Abschnitt diskutiertwerden, eingeführt werden kann. Die Einführung des unteren Cutoffs liefert eine Performance-verbesserung ohne wesentlich die Genauigkeit der Ergebnisse zu verschlechtern.

68


Wird das Temperaturverhalten der Verteilung der Diagrammordnungen untersucht, so erhältman für ein 2 2-Hubbard-Cluster Abbildung 4.12. Hier ist neben den Cutoffs und der mittle-

ren Ordnung auch die Standardabweichung ∆k =¼`k2e − `ke2 durch Fehlerbalken dargestellt.

Es zeigt sich, dass das obige Cutoff-Kriterium deutlich konservativere Grenzen liefert als diegemessene Standardabweichung.

Messung von Observablen

Wurde die approximative Verteilung g konstruiert, so ist es nicht nur möglich die großkano-nische Zustandssumme Ξ für alle Wechselwirkungsstärken U zu berechnen, sondern auch dieMatsubara-Funktion G und Observablenerwarungswerte für alle Wechselwirkungsstärken überMonte-Carlo-Mittelung zu bestimmen. Um dies zu verstehen, betrachte man zunächst nochmalden Observablenerwartungswert (4.2.10) im CT-QMC-Algorithmus, der auch repräsentativ fürdie Matsubara-Funktion steht.Wird im Folgenden angenommen, dass kein Vorzeichenproblem6 existiert, lässt sich der Erwar-tungswert wie folgt für den Wang-Landau-Algorithmus umschreiben:

` O e = PkPCkζUCkOCk

PkPCkζUCk =

1Ξ~Ξ0

Qk

Uk gkQCk

ζ1Ckgk

PCk

ζ1Ckgk OCk

PCk

ζ1Ckgk

.

(4.3.13)

Nun lässt sich erkennen, dass die Observable O mit Hilfe des Metropolis-Algorithmus für jedeOrdnung k separat bestimmen lässt, da diese einem Erwartungswert bezüglich der Verteilungζ1Ck gleicht:

Ok = PCkζ1CkOCkPCk

ζ1Ck. (4.3.14)

Man beachte, dass trotz des Samplings mit einer Gleichverteilung bezüglich der Diagrammord-nung k immer noch Importance-Sampling bezüglich der Konfigurationen Ck existiert.Damit ergibt sich also für den Erwartungswert der Observablen bei einer WechselwirkungsstärkeU :

` O e = 1Ξ~Ξ0

Qk

Uk wkOk Pk Uk gkg0 Ok

Pk Uk gkg0

(4.3.15)

Offensichtlich lässt der Wang-Landau-Algorithmus es zu, sowohl die großkanonische Zustandss-umme als auch die Observablenerwartungswerte und die Matsubara-Funktion für jede beliebigeWechselwirkungsstärke U berechnen, ohne jedes Mal erneut eine entsprechende Markov-Ketteaufzubauen.Die Messung von Ok kann entweder durch einen Random-Walk bezüglich der Ordnungenk und der dazugehörigen Konfigurationen Ck mit Zuordnung der Werte OCk zu der ent-sprechenden Ordnung und anschließender Mittelung für jede Ordnung k oder durch separateMarkov-Ketten für jede der zu betrachtenen Ordnungen, wobei die Übergänge durch Verän-dern eines Vertex realisiert werden können, erfolgen. Die erstgenannte Variante sollte bevorzugtwerden, da Korrelationen zwischen den verschiedenen Ordnungen durch die separate Mittelungunterdrückt werden. Dadurch werden bei Benutzung einer Markov-Kette für alle zu betrach-tenden Ordnungen weniger Übergänge benötigt als bei der Verwendung von für jede Ordnung6Mit Berücksichtigung des Vorzeichens s der Zustandsverteilung ζ lässt sich auf analogem Weg ein entspre-

chender Ausdruck für den Observablenerwartungswert finden.

69


Abbildung 4.12: Temperaturverhalten der Verteilung der Diagrammordnungen: Für große inverse Temperatu-ren β verhalten sich sowohl mittlere Ordnung `ke als auch die Standardabweichung ∆k linearund folglich auch die Cutoffs (oben). Die lineare Verschiebung der mittleren Ordnung unddie wachsende Breite der Verteilungen wird in der unteren Abbildung besonders deutlich.Hier sind die Wahrscheinlichkeitsverteilungen der Ordnungen für verschiedene Temperaturenabgebildet.

70


Abbildung 4.13: Abhängigkeit der Verteilung der Diagrammordnungen von der Wechselwirkungsstärke Ueines halbgefüllten 2 2-Hubbard-Clusters bei β = 10: Die Wahrscheinlichkeitsverteilungenpk der Ordnungen verschiedener Wechselwirkungsstärken zeigen einen großen Überlapp fürkleine Differenzen ∆U .

separaten Markov-Ketten.

Für den Monte-Carlo-Mittelwert Ok lässt sich zwar nach (4.1.21) ein statistischer Fehlerangeben, dennoch scheint zunächst die Gesamtfehlerabschätzung von `Oe problematisch, dakein statistischer Fehler auf gk angegeben werden kann. Die Möglichkeit den Gesamtfehlerüber das Fehlerfortpflanzungsgesetz zu berechnen ist somit nicht gegeben. Eine Lösung diesesProblems ist denkbar einfach: Man berechnet mehrfach die gewünschte Größe für verschiedeneSätze von Zufallszahlen. Da die resultierenden Ergebnisse als unkorreliert angesehen werdenkönnen, lässt sich dann der statistische Fehler nach (4.1.12) abschätzen.

Eine entscheidende Frage ist es, ab wann es sinnvoll ist, den Wang-Landau-Algorithmus auchfür Observablenmessungen zu benutzen. Da für jede Ordnung eine entsprechend gute Statistikvorliegen sollte, ergibt sich der Nachteil der Messungen im Wang-Landau-Algorithmus: Sehrgroße Ordnungen, die ein geringes Gewicht besitzen und vom Monte-Carlo-Algorithmus so-mit relativ selten besucht werden, werden im Wang-Landau-Algorithmus annähernd genausooft besucht wie sehr niedrige. Da allerdings die Berechnungszeit der Akzeptanzwahrschein-lichkeiten kubisch mit der Ordnung steigt, erweist sich der Wang-Landau-Algorithmus als derlangsamere Algorithmus, sofern nicht Observablen als quasikontinuierliche Funktionen von Ubestimmt werden sollen. Bei Betrachtung der Verteilung der Diagrammordnungen in Abhän-gigkeit von der Wechselwirkungsstärke U in Abbildung 4.13 wird deutlich, dass je kleiner dieDifferenz in U der zu betrachtenen Systeme ist, desto größer wird der Überlapp zwischen denVerteilungen. In dem Überlappungsbereich werden auch mit separaten Monte-Carlo-Messungeninsgesamt Ordnungen mit geringem Gewicht relativ oft besucht, sodass der Performancevorteildes Monte-Carlo-Algorithmus verschwindet. Durch dieses Oversampling der Überlappbereichemüssen sogar unnötig lange Markov-Ketten generiert werden, um eine gewünschte Genauigkeitzu erreichen und der Wang-Landau-Algorithmus stellt dann die bessere Wahl dar.

71


Liegt Teilchen-Loch-Symmetrie vor, so existiert kein Vorzeichenproblem im Ein-Band-Hubbard-Modell. Da dann aber nur gerade Ordnungen beitragen, sind nur Übergänge k Ð k2 erlaubt.Für den Wang-Landau-Algorithmus führt dies zu einer Performanceverbesserung, weil nur nochdie Hälfte der Ordnungen besucht werden müssen und vor allem die mittlere Ordnung `keim Vergleich zur Polarisationsmethode kleiner ist. Man betrachte dazu nochmals Gleichung(4.2.11). Auch wenn δ beliebig klein gewählt werden kann, ohne das Vorzeichenproblem hervor-zurufen, besteht dann das Problem, dass ungerade Ordnungen nur ein sehr geringes Gewichthaben. Dadurch werden nur sehr wenige Übergänge akzeptiert und folglich sind die Messda-ten stark korreliert, wodurch sehr lange Markov-Ketten benötigt werden. Um dieses Problemzu vermeiden, muss δ also hinreichend groß gewählt werden, um Übergänge zu benachbartenOrdnungen zu realisieren, wodurch die mittlere Ordnung um βUNcδ

2 ansteigt (vgl. Abbildung4.14).

Abbildung 4.14: Abhängigkeit der Diagrammordnungen vom Parameter δ eines halbgefüllten 2 2-Hubbard-Clusters bei U = 1 und β = 10: Für kleiner werdende Werte für δ nehmen sowohl die mittlereOrdnung sowie die Breite der Verteilung ab. Außerdem verlieren ungerade Ordnungen anGewicht.

Auch die Anwesenheit von Badplätzen im System hat einen entscheidenden Einfluss auf die Ver-teilung und damit auf die mittlere Ordnung. Betrachtet man Abbildung 4.15, so erkennt man,dass sich die Lage des Maximums der Verteilung für stärkere Hybridisierungen zu kleinerenOrdnungen verschiebt und damit auch die mittlere Ordnung abnimmt. Die Badplätze führenalso nicht nur zur Milderung des Vorzeichenproblems, sondern liefern auch sonst noch eine Per-formancesteigerung. Diese Verschiebung lässt sich dadurch erklären, dass durch das zusätzlicheHopping die Elektronen nicht mehr so stark lokalisiert sind und der Einfluss der Wechselwir-kung, mit dem die mittlere Ordnung nach Gleichung (4.2.11) gekoppelt ist, nachlässt. AnhandAbbildung 4.15 zeigt sich aber auch, dass die Verschiebung für kleine Hybridisierungsstärken Vam größten ist und dass es für den Limes V Ð ª zu einer Sättigung der mittleren Ordnungkommt. Der Grenzfall V Ð ª ist somit nicht mit dem Limes U 0 zu verwechseln. Bereitsfür den analytisch lösbaren Fall einer Impurity mit nur einem zusätzlichen Badplatz führt der

72


Grenzfall V Ðª nicht zu einer freien Greenfunktion. Dies ist leicht einsehbar, da die Green-funktion für diesen Grenzfall weiterhin vier Pole aufweist, wogegen die freie Greenfunktion nurzwei besitzt [63].

Abbildung 4.15: Abhängigkeit der Verteilung der Diagrammordnungen von der Hybridisierungsstärke V eineshalbgefüllten 2 2-Hubbard-Clusters mit je einem Badplatz pro korreliertem Platz: Einezunehmende Hybridisierung führt zu einer Verschiebung der mittleren Ordnung und zu einerabnehmenden Breite der Verteilung.

73


74

5 Der Mott-Übergang und derHochtemperatur-Crossover im2D-Hubbard-Modell

Eins der am meisten faszinierenden Effekte starker Wechselwirkungen zwischen itinerantenElektronen ist das isolierende Verhalten, das induziert wird durch die Korrelationen zwischenden Elektronen. Das Verständnis der isolierenden Phase und auch des Übergangs von einemkorrelierten paramagnetischen Metall zu einem Mott-Isolator ist wichtig für viele Übergangs-metalloxide, insbesondere von Komponenten von kupratbasierten Hochtemperatursupraleitern.Der Mott-Übergang wird durch Gittermodelle mit rein lokalen Wechselwirkungen beschrieben,wie dem Ein-Band-Hubbard-Modell. Allerdings sind Korrelationen im Allgemeinen nicht-lokalerNatur oder gar langreichweitig. Es ist eine im höchsten Maße nicht-triviale Frage, welche Mo-dellerweiterung die Physik des Mott-Übergangs, der durch die lokalen Korrelationen dominiertwird, weitestgehend reproduziert. Bereits lokale Approximationen liefern die wesentliche Physikdieses Phasenübergangs.Das Verständnis des Mott-Übergangs innerhalb der am Temperaturnullpunkt T = 0 metastabi-len paramagnetischen Phase wird benötigt, um den Crossover zwischen Metall und Isolator beiendlichen Temperaturen oberhalb der Néel-Temperatur zu erklären. Somit soll zunächst auf denMott-Übergang im Allgemeinen und anschließend auf die bereits vorhandenen Erkenntnisse fürdas zweidimensionale Hubbard-Modell eingegangen werden, bevor die demonstrativen Ergeb-nisse der Kombination von VCA und wcCT-WL für den Hochtemperatur-Crossover vorgestelltwerden.

5.1 Grundlagen des Mott-Übergangs

Erstmals wurde 1949 von N.F. Mott [76] veröffentlicht, dass starke elektronische Korrelatio-nen ein isolierendes Verhalten eines Systems verursachen können, das durch die konventionelleBandtheorie als ein normales Metall beschrieben wird. Die grundlegende Idee ist, dass für einnicht-entartetes halbgefülltes Valenzband die Elektronen wegen der starken lokalen Coulomb-Abstoßung U lokalisiert sind. Im Grundzustand ist jeder Gitterplatz exakt von einem Elektronbesetzt, da eine Doppelbesetzung energetisch ungünstig ist. Um ein zusätzliches Elektron demSystem hinzuzufügen, muss ungefähr die Energie U aufgewendet werden, da die Elektronen nurüber besetzte Plätze hüpfen können (Abbildung 5.1a). Das führt zu einem oberen Hubbard-Bandim Ein-Teilchen-Anregungsspektrum, das durch eine Lücke, dem so genannten Hubbard-Gap,der Größenordnung U von dem unteren Band getrennt ist. Das letztere korrespondiert mit ei-nem Prozess, bei dem Elektronen aus dem System entfernt werden (Abbildung 5.1b).Betrachtet man das Hubbard-Modell in Abhängigkeit der Besetzung des Systems, so verursachtdie lokale Wechselwirkung einen Sprung im chemischen Potential bei einer Besetzung pro Git-terplatz von n = 1. Für dieses halbgefüllte System trennt der Hubbard-Gap das besetzte vomunbesetztem Spektrum. Mit kleiner werdender Wechselwirkungsstärke U muss dann ein Über-gang von der isolierenden zu der metallischen Phase erfolgen. Damit stellt der Mott-Übergang

75

5 Der Mott-Übergang und der Hochtemperatur-Crossover im 2D-Hubbard-Modell

Abbildung 5.1: Elektronen bewegen sich (kohärent) als Doppelbesetzungen im oberen (a) und als Löcher inderm unteren Hubbard-Band, wenn die Zahl der Doppelbesetzungen und Löcher näherungs-weise bei starker Kopplung erhalten bleibt. Abb. entnommen aus Ref. [78].

ein Beispiel für einen Phasenübergang am Temperaturnullpunkt T = 0 dar.

Das möglicherweise einfachste Modell für den Mott-Übergang stellt das Hubbard-Modell dar.Für starke Wechselwirkungen U Q t und Halbfüllung kann das Hubbard-Modell auf das Heisen-berg-Modell mit einer antiferromagnetischen Austauschwechselwirkung abgebildet werden. Da-her erwartet man langreichweitige antiferromagnetische Ordnung im Grundzustand bei Halb-füllung. Die magnetische Ordnung führt zu einem Slater-Gap im Spektrum und folglich wirdeine isolierende Phase erreicht, wenn der Gap die besetzten von den unbesetzten Zuständenvollständig separiert. Abhängig davon, ob lokale magnetische Momente für Temperaturen überder Néel-Temperatur vorhanden sind, unterscheidet man zwischen einem Mott-Heisenberg- undeinem Slater-Isolator. In beiden Fällen ist die isolierende Phase eng verknüpft mit der lang-reichweitigen magnetischen Ordnung und der Metall-Isolator-Übergang wird als ein thermody-namischer Phasenübergang beschrieben. Deshalb muss der antiferromagnetische (Slater oderMott-Heisenberg) Isolator klar von dem Mott-Hubbard-Isolator unterschieden werden. Wegenden starken elektronischen Korrelationen wird der Mott-Hubbard-Isolator charakterisiert durchstarke ungeordnete lokale magnetische Momente.

5.2 Der Mott-Übergang am Temperaturnullpunkt

Kürzlich wurde innerhalb der VCA mit einer Plakette bestehend aus vier korrelierten Gitter-plätzen und je einem Badplatz pro korrelierten Platz als Referenzsystem der Mott-Übergangdes 2D-Hubbard-Modells bei Halbfüllung µ = U~2 am Temperaturnullpunkt T = 0 untersucht[83], wobei die Lanczos-Methode als Cluster-Solver benutzt wurde.Idealerweise sollten neben einer möglichst großen Anzahl von korrelierten Plätze auch möglichstviele Badplätze vorhanden sein, um bei der Parameteroptimierung einen möglichst großen Raumder Testselbstenergien durchlaufen zu können, damit eine optimale Approximationsgüte erreichtwird. Dementsprechend ist im Sinne der cDMFT eine Einbettung der korrelierten Plätze in einKontinuum von Badplätzen das Optimum. Allerdings existiert für T = 0 kein Cluster-Solver fürein solches System. Da aber die statischen Größen und das thermodynamische Phasendiagrammbereits mit Hinzunahme weniger Badplätze die wesentliche Physik widerspiegeln, ist eine Studiemit nur einem zusätzlichen Badplatz für das qualitative Verständnis des Mott-Übergangs unterUmständen ausreichend. Dies zeigten bereits Rechnungen mit einer Impurity mit lediglich ei-nem zusätzlichen Badplatz, die das DMFT-Phasendiagramm des Mott-Übergangs weitgehendreproduzierten [24], aber auch Cluster-Näherungen in einer Dimension [31] haben dies bestätigt.Die bestehende Teilchen-Loch-Symmetrie fixiert bereits die optimalen Werte der Onsite-Energiender korrelierten Plätze (εopt

c = 0) und der Badplätze (εoptb = µ = U~2), was anhand der statio-

nären Punkte des SFT-Funktionals nachvollzogen werden kann. Des Weiteren zeigte sich, dassdie Abweichungen der optimalen Werte des Hoppings zwischen den korrelierten Plätzen t′ bzw.zwischen den Badplätzen t′′ von den jeweiligen Werten des Originalsystems klein sind gegenüber

76

5.2 Der Mott-Übergang am Temperaturnullpunkt

der Änderung in der Hybrisierung, also in dem Hopping V zwischen den korrelierten Plätzenund den Badplätzen. Wird nun der Parameterraum durch Setzen von t′ = t und t′′ = 0 aufeine Dimension reduziert, so führt dies zu einer Änderung in dem optimalen Wert für V vonweniger als einem Prozent, so dass der Unterschied des Wertes des SFT-Funktionals und somitder Unterschied in dem approximativen Wert für das großkanonische Potential vernachlässigbarklein ist.Wird die Optimierung des SFT-Funktionals bezüglich V jeweils für verschiedene Wechselwir-kungsstärken U durchgeführt, so lässt sich der wechselwirkungsgetriebene Mottsche Metall-Isolatorübergang studieren. Man betrachte dazu Abbildung 5.2.

Abbildung 5.2: SFT-Funktional pro Gitterplatz des Originalsystems mit Variationsparameter V geshiftet umeine Konstante µN für verschiedene U . Die Kreise zeigen die stationären Punkte. GefüllteKreise: stabiles Metall (Blau) und stabiler Isolator (Rot). Schattierte Kreise: metastabile Pha-sen, insbesondere eine weitere metallische Phase (Grün). Bei Uc findet ein diskontinuierlicherMetal-Isolator-Übergang statt. Abb. entnommen aus Ref. [83].

Für U < Uc2 6.35 existiert eine metallische Phase mit einer relativ großen optimalen Hybri-disierung Vopt der Plakette, die mit wachsendem U abfällt. Für U A Uc1 4.6 existieren zweiweitere stationäre Punkte des SFT-Funktionals. Dabei repräsentiert der eine bei sehr kleinenWerten des Variationsparameters V eine isolierende Phase und der andere eine weitere metalli-sche Phase, die an die dritte Lösung aus DMFT-Rechnungen bei endlichen Temperaturen erin-nert [?]. Dabei wird die Unterscheidung der Charakteristik anhand der lokalen Green-FunktionGiiiω und der Selbstenergie Σkiω vorgenommen. Abbildung 5.3 zeigt das unterschiedlicheVerhalten der lokalen Green-Funktion (links) und der Selbstenergie (rechts) für die drei Phasenim Koexistenzbereich bei Uc1 < U = 5.8 < Uc2.Nach Fouriertransformation der Selbstenergie des Clusters erkennt man, dass die Selbstenergiefür den Cluster-Impuls k = 0,0 regulär ist, während sie für k = π,0 einen Pol bei ω = 0besitzt. Dies führt zu einer verschwindenden lokalen Green-Funktion Giiiω für ω 0 inder isolierenden Phase. Die metallische Lösung wird hingegen für ω 0 durch eine endlichelokale Green-Funktion Giiiω und eine reguläre Selbstenergie Σk charakterisiert, wobei diek-Abhängigkeit deutlich schwächer ist als in der isolierenden Lösung für U = 5.8.Kehrt man nun wieder zur Abbildung 5.2 zurück, so erkennt man einen diskontinuierlichen

77


Abbildung 5.3: Imaginärteile der lokalen Green-Funktion Giiiω und der Selbstenergie Σkiω für dieCluster-Impulse k = 0,0 und k = π,0 bei U = 5.8. Abb. entnommen aus Ref. [83].

Metall-Isolator-Übergang bei einem kritischen Wert von Uc = 5.79, also einen Phasenübergangerster Ordnung. Die dritte Phase (grün), die allerdings aufgrund ihrer höhren Grundzustands-energie metastabil ist, ist in dem ganzen Koexistenzbereich metallischer Natur und verbindet dasstabile Metall mit dem Isolator. Dies impliziert einen kontinuierlichen Metall-Isolator-Übergangmit einem kritischen Punkt bei Uc1. Aufgrund der Metastabilität der zweiten metallischen Lö-sung (Grün) bleibt dieser Übergang nicht sichtbar, so dass ein Hidden Critital Point (HCP)vorliegt.Werden nun dem Cluster noch weitere Badplätze hinzugefügt, ist ein HCP nicht aufzufinden.Dennoch bleibt der Phasenübergang diskontinuierlich, also erster Ordnung [83].

5.3 Der Mott-Übergang bei endlichen Temperaturen

Obwohl der Mott-Übergang bei endlichen Temperaturen T A 0 insbesondere über DMFT aus-giebig untersucht wurde, blieb auch dieser für die neuen Cluster-Methoden nicht unbeachtet.Wie am Temperaturnullpunkt ergeben sich bei den Cluster-Methoden auch für endliche Tem-peraturen Werte für die kritische Wechselwirkungsstärke UcT , die deutlich kleiner sind alsdie, die bisher aus DMFT-Rechnungen bekannt waren. Die starken kurzreichweitigen antiferro-magnetischen Korrelationen, die durch das Intraclusterhopping in den Cluster-Methoden mit-berücksichtigt werden, führen zu diesem Verhalten. Diese kritische Wechselwirkungsstärke wirdfür auf kurzer Distanz stärker frustrierte Systeme wachsen, z.B. durch Einbindung eines Über-nächstnachbarhoppings [85].Um die wesentlichen Änderungen des Phasendiagramms aus den Cluster-Methoden gegenüberdem aus der DMFT zu diskutieren, betrachte man jenes aus cDMFT-Rechnungen [81] mit einer4-Platz-Plakette stammende Phasendiagramm des (paramagnetischen) 2D-Hubbard-Modellsbei Halbfüllung in Abbildung 5.4. Für Wechsewirkungsstärken U < Uc2T findet man eine me-tallische Lösung, während für U A Uc1 eine Isolatorlösung existiert. Die beiden ÜbergangslinienUc1T und Uc2T treffen sich an einem Endpunkt bei einer Temperatur TMIT 0.09 und

78

5.3 Der Mott-Übergang bei endlichen Temperaturen

Abbildung 5.4: Phasendiagramm des paramagnetischen halbgefüllten 2D-Hubbard-Modells resultierend auscDMFT-Rechnungen mit einer 4-Platz-Plakette. Der Koexistenzbereich ist schattiert. Diegelb-gestrichelte Linie zeigt den Crossover vom Metal zum Isolator, wohingegen die schwarz-gestrichelte Linie in dem Koexistenzbereich die Phasentrennlinie darstellt, bei der die beidenstabilen Phasen das gleiche großkanonische Potential aufweisen. Abb. entnommen aus Ref.[81].

einer Wechselwirkungsstärke UMIT 6.05. Die Lage dieses Endpunktes hat sich also durch dievom Cluster mitberücksichtigten Korrelationen verändert (vgl. UDMFT

MIT 9.35). Dadurch dassdie DMFT die wesentliche Physik des Mott-Übergangs bereits wiedergibt, ändert sich innerhalbder Cluster-Methoden nichts daran, dass es sich bei dem Mottschen Metall-Isolator-Übergangum einen diskontinuierlichen Phasenübergang handelt. Allerdings weicht die Form des Koexis-tenzbereichs signifikant von dem aus DMFT-Rechnungen resultierenden ab. Dort gewann dasMetall mit tieferen Temperaturen, da das in Erscheinungtreten von itineranten Quasiteilchenin dem Mott-Gap die freie Energie von stark ungeordneten Mott-Zuständen verringert. Bei dercDMFT hat der Mott-Isolator bei tiefen Temperaturen wegen der kurzreichweitigen Singlett-bildung eine kleine Entropie. Die metallische Phase hat folglich mit einem völlig anderen Typvon Mott-Isolator zu konkurrieren und ein schmales Leitungsband kann die Energie von die-sem Typ von Mott-Isolator nicht verringern, sodass der Isolator mit tieferen Temperaturengewinnt. Damit biegt sich mit Verringern der Temperatur auch die wahre Phasentrennlinie,bei der die beiden stabilen Phasen das gleiche großkanonische Potential aufweisen, zu kleinerenWechselwirkungsstärken hin. Im Gegensatz zu dem DMFT-Phasendiagramm, in dem das Me-tall weitestgehend überwiegt, ist somit der Isolator in einem Großteil des Koexistenzbereichesstabil.

79


5.4 Die stochastisch ausgewertete VCA und derHochtemperatur-Crossover

In diesem Abschnitt soll nun anhand der Untersuchung des Hochtemperatur-Crossovers deshalbgefüllten zweidimensionalen Hubbard-Modells die Funktionstüchtigkeit der Kombinationvon VCA mit dem in Kapitel 4 vorgestellten wcCT-WL-Algorithmus als Cluster-Solver aufge-zeigt werden.In Abschnitt 4.3 wurde bereits diskutiert, dass der wcCT-WL-Algorithmus mit nur einer Rech-nung (quasi-)kontinuierliche Ergebnisse in U liefert. Zusammen mit der Stärke der VCA, die imVergleich zu den Selbstkonsistenzrechnungen der cDMFT oder auch der DCA weniger Rechnun-gen für die Optimierung der Variationsparameter benötigt, um ähnlich gute Approximationenzu bekommen, liefert die Kombination VCA/wcCT-WL einen neuen Ansatz für endliche Tem-peraturen, der prädestiniert ist, um Größen in Abhängigkeit von der WechselwirkungsstärkeU zu studieren oder um gar das Phasendiagramm des Mott-Übergangs zu bestimmen. Insbe-sondere bietet die neue Methode die Möglichkeit erstmals die für die cDMFT und der DCAunzugängliche Phasentrennlinie UcT sofort zusammen mit der Berandung des Koexistenzbe-reiches durch Uc1T und Uc2T bestimmen.Da die stochastische Methode wcCT-WL in einem Potenzgesetz skaliert, lassen sich ganz neueApproximation durch wesentlich größere Cluster innerhalb der VCA entwickeln. Da allerdingsder Rechenaufwand für diesen Cluster-Solver mit fallender Temperatur ansteigt, soll zunächstnur das Hochtemperaturverhalten des zweidimensionalen Hubbard-Modells mit einem kleinen2 2-Cluster mit je einem Badplatz pro korrelierten Platz (analog zu Abschnitt 5.2) studiertwerden:

Die Wechselwirkung zwischen den Elektronen führt zu magnetischen Momenten. Im Allge-meinen werden diese Momente weit oberhalb ihrer Ordnungs- bzw. Néel-Temperatur TNUgebildet, unter der das System ein antiferromagnetischer Mott-Heisenberg-Isolator oder einMetall ist. Damit liefert das Leitungsverhalten bei Temperaturen über der Néel-Temperatureine interessante Fragestellung. Ein Material kann effektiv auch über TNU isolierend blei-ben (Mott-Hubbard-Isolator). Solch ein Verhalten kann als Konsequenz eines Phasenübergangsbei T = 0 verstanden werden: Auch wenn keine langreichweitige Ordnung der Momente vor-liegt, führen die elektronischen Korrelationen dazu, dass das paramagnetische Metall bei einerbestimmten Wechselwirkungsstärke Uc in einen paramagnetischen Mott-Hubbard-Isolator über-geht. Dabei besteht keine scharfe Trennung zwischen dem Metall und dem Isolator, die nichtals unterschiedliche Phasen im Sinne der statistischen Physik angesehen werden. Stattdessenwird dieser Übergang als Crossover bezeichnet.Dieser Crossover geschieht kontinuierlich, und für steigende Temperaturen wird der Unterschiedzwischen dem Metall und dem Isolator immer kleiner. Eine Untersuchung des Crossovers bei derTemperatur T = 0.5 mittels VCA mit einem durch wcCT-WL gelösten 2 2-Hubbard-Cluster,an dessen Plätze je ein Badplatz angebunden ist, zeigt dies recht deutlich auf:Der kontinuierliche Übergang äußerst sich darin, dass das SFT-Funktional für alle Wechselwir-kungsstärken U lediglich nur einen nicht-trivialen stationären Punkt aufweist (Abbildung 5.5).Dabei verschiebt sich die optimale Hybridisierungsstärke für ein wachsendes U näherungsweiselinear zu kleineren Werten. Eine kleinere optimale Hybridisierung lässt sich durch die stärkereLokalisierung der Elektronen erklären, die durch die größere Wechselwirkungsenergie entsteht,die aufgebracht werden muss, um eine Doppelbesetzung eines Gitterplatzes zu realisieren.Um nun die erhaltene Lösung zu charakterisieren, bietet es sich an, das großkanonische Poten-tial Ω als Funktion der Wechselwirkungsstärke U zu betrachten. Abbildung 5.6 (oben) zeigteinen glatten Verlauf von Ω in dem aus cDMFT-Rechnungen [81] erwarteten Crossoverbereich

80

5.4 Die stochastisch ausgewertete VCA und der Hochtemperatur-Crossover

Abbildung 5.5: SFT-Funktional als Funktion von der Hybridisierung für verschiedene Wechselwirkungsstärkenbei einer Temperatur T = 0.5. Die roten Pfeile zeigen die approximative Lage des Minimums.Als Originalsystem diente ein 40 40-Hubbard-Modell, das durch 2 2-Cluster, an deren kor-relierte Plätze je ein Badplatz angebunden ist, parkettiert wird. Für die Rechnungen wurdenfolgende Parameter gewählt: δ = 0.5001; Feinheit des τ -Meshs der Observablen: ∆τobs = 10−4;Cutoff-Frequenz ωc = ω60. Nach jeweils 1000 Fast-Updates (siehe Abschnitt 4.2.3) wurd dieMatrix Dσ wieder neu aufgebaut. 2000 Monte-Carlo-Schritte pro Sweep (Nach jedem Sweepfindet eine Messung statt.); 5 ċ104 Messungen pro Diagrammordnung; untere Cutoff-Ordnungku

c = 0, obere Cutoff-Ordnung koc = 60

(3 B U B 6; vgl. Abbildung 5.4) ohne jeglichen Knick auf, so dass eine Unterscheidung zwischeneinem isolierenden oder metallischen Zustand nicht möglich ist. Auch bei Betrachtung der Ab-leitung (Abbildung 5.6 unten), die die Doppelbesetzung1 repräsentiert und ein empfindlicheresMaß für die Charakterisierung der Lösungen darstellt, zeigt sich eine glatte Funktion. Diese istjedoch konkav, was einer metallischen Lösung entspricht. Da für U ª die Doppelbesetzung

1Das Bestimmen der Doppelbesetzung des Originalsystems sollte innerhalb der VCA über die Ableitung desgroßkanonischen Potentials nach der Wechselwirkungsstärke erfolgen und nicht über Messung der Cluster-Doppelbesetzung. Diese sollte sich für sehr wenige Badplätze durchaus von der Doppelbesetzung des Origi-nalsystems unterscheiden. Dies kann als Artefakt des fehlenden kontinuierlichen Bades angesehen werden.

81


Abbildung 5.6: Oben: großkanonisches Potential Ω pro Gitterplatz als Funktion der WechselwirkungsstärkeU für zwei Referenzsysteme (Nc = 1 bzw. Nc = 4 mit jeweils nb = 1). Unten: Doppelbesetzung`de als Funktion der Wechselwirkungsstärke U für die beiden Referenzsysteme von oben. Auf-grund des konkaven Verlaufs ist nur eine metallische Lösung in dem betrachteten Bereich zuerkennen. In der Inbox ist die Ableitung der Doppelbesetzung dargestellt. Ein Parabel-Fit andiese liefert als mögliche Wendestelle der Doppelbesetzung, die die kritische Wechselwirkungs-stärke repräsentiert, Uc 5.9. Weiterhin sind als Vergleichsdaten die T=0-Doppelbesetzungender metallischen und isolierenden Phase [84], sowie die T=0.5-Doppelbesetzung bei U = 5 re-sultierend aus DCA-Rechnungen von E. Gull et al. [82] eingezeichnet. Parameter der Nc = 1-Rechnungen: δ = 0.5001, ∆τobs = 10−2; nach jeweils 1000 Fast-Updates in Folge wurde dieMatrix Dσ wieder neu aufgebaut; 106 Messungen pro Ordnung; ku

c = 0, koc = 16, CPU-Zeit

720 min jeweils für einen Wert der Hybridisierungsstärke V gerechnet auf einem Intel Xeon2.83 GHz-Prozessor.

82


langsam verschwinden muss, ist ein Übergang von einem konkaven zu einem konvexen Verlaufzu erwarten. Dieser konvexe Verlauf der Doppelbesetzung repräsentiert dabei den Isolator.Da nun die Notwendigkeit einer Wendestelle in der Doppelbesetzung erklärt wurde, ist zu erwar-ten, dass diese sich entweder am Ende des betrachteten Intervalls oder sogar bei noch größerenWechselwirkungsstärken befindet. Um eine mögliche Entwicklung einer Wendestelle zu analysie-ren, betrachte man die Ableitung der Doppelbesetzung (siehe Inbox von Abbildung 5.6 unten).Durch den Übergang von einem konkaven zu einem konvexen Abschnitt der Doppelbesetzungwird ein Minimum in ihrer Ableitung erwartet. Ein Parabel-Fit an die entsprechenden Datendieser Ableitung ergibt als kritische Wechselwirkungsstärke des Crossovers UcT = 0.5 5.9.Allerdings weist die Ableitung der Doppelbesetzung sehr großes Rauschen auf und der statisti-sche Fehler ist unbekannt, so dass dieser Wert für den Crossover nicht sehr zuverlässig erscheint.Die Auswertung ist auch deshalb so schwierig, da der Unterschied zwischen dem Isolator unddem Metall nur marginal ist und daher die Doppelbesetzung am Wendepunkt sehr flach ver-läuft. Bei sinkender Temperatur wird aber die Steigung der Doppelbesetzung an der Wendestelleausgeprägter sein. Folglich wird bei gleich bleibenden absoluten Fehler in der Doppelbesetzungdie Bestimmung der Wendestelle zuverlässiger werden.

Abbildung 5.7: Imaginärteil der lokalen Matsubara-Funktion für verschiedene Wechselwirkungsstärken: FürU = 6 weist die Matsubara-Funktion eine leichte Tendenz zum Verschwinden für kleiner wer-dende Frequenzen auf und repräsentiert eine isolierende Lösung.

Wird jedoch mit dem Verlauf des Imaginärteils der lokalen Matsubara-Funktion, analog zumAbschnitt 5.2, ein weiteres Charakterisierungskriterium herangezogen, so kann man aus Abbil-dung 5.7 unter Berücksichtigung der sehr großen Abstände zwischen den Matsubara-Frequenzenvermuten, dass für U = 6.0 die Matsubara-Funktion eine leichte Tendenz zum Verschwinden fürkleiner werdende Frequenzen entwickelt und daher eine isolierende Lösung charakterisiert. So-mit bestätigt dies die Abschätzung der kritischen Wechselwirkungsstärke des Crossovers überdie Wendestelle der Doppelbesetzung (UcT = 0.5 5.9). Damit stimmt die hier gefundendekritische Wechselwirkungsstärke sehr gut überein mit dem Ergebnis von M. Vekic und S.R.White (UcT = 0.5 6.0, [87]), die einen isolierten 8 8-Cluster untersuchten.

83


Allerdings weist die Matsubara-Funktion ein starkes Rauschen auf, woraus auch die verrausch-ten Ergebnisse für das großkanonische Potential bzw. der daraus resultierende Doppelbesetzungfolgt, da die Matsubara-Funktion nach (3.4.11) zur Auswertung des SFT-Funktionals benötigtwird. Das großkanonische Potential des Clusters scheint hingegen nicht allzu stark fehlerbehaftetzu sein. Dies ist darauf zurückzuführen, dass die Verteilung der Ordnungen der Diagramment-wicklung in der wcCT-WL-Methode sehr gut bestimmt werden kann und somit auch eine sehrgute Approximation der Zustandssumme nach (4.3.12) möglich ist. Aus der Zustandssummefolgt dann nach (2.1.1) auch das großkanonischen Potentials des Clusters. Bei der Messung derMatsubara-Funktion wird jedoch die Verteilung der einzelnen Diagramme bei fester Ordnungbenötigt. Die Update-Schritte des Algorithmus sollten zwar die Diagramme mit großem Gewichtliefern, dennoch ist aufgrund der Größe des Konfigurationsraums eine umfangreiche Anzahl anMessungen nötig, um eine gute Approximation der Matsubara-Funktion zu realisieren. Manbeachte, dass der Konfigurationraum mit steigender Ordnung stark anwächst, so dass für großeOrdnungen wesentlich mehr Realisierungen für eine gute Approximation nötig sind. Dies wirdumso wichtiger je kleiner die betrachte Temperatur und je größer die betrachte Wechselwir-kungsstärke und Clustergröße wird. Außerdem wurde in Abschnitt 4.3 erklärt, dass mit stärkerwerdender Hybridisierung V die mittlere Diagrammordnung bis zu einem Sättigungswert kleinerwird. Diese Verschiebung ist insbesondere für kleine V ein nicht zu vernachlässigender Effekt.Folglich führt dies bei fester Anzahl der Messungen zu einem anwachsenden statistischen Fehlermit schwächer werdender Hybridisierung (siehe Abbildung 5.8). In Abbildung 5.5 wurden daherdie Ergebnisse für V < 0.1 wieder verworfen. Es ist zu empfehlen, die Statistik für V = 0 zuoptimieren. Um eine gute Statistik zu erreichen, müssen also sehr lange Markov-Ketten erzeugtwerden. Daher wird also viel Rechenleistung benötigt. Der Speicherplatzbedarf ist hingegen, wiefür stochastische Methoden üblich, verhältnismäßig klein. Bei den T=0.5-Rechnungen wurde dasSFT-Funktional für die 13 verschiedenen Werte für die Hybridisierungsstärke parallel auf 13Intel-Xeon-Prozessoren mit 2.83 GHz berechnet. Die genauen Parameterwerte entnehme mander Bildunterschrift von Abbildung 5.5. Die Rechnungen dauerten jeweils ca. 27000 Minutenpro Hybridisierungsstärke. Eine Verbesserung der Effizienz lässt sich vermutlich durch Benut-zung eines groberen τ -Meshs für die Observablenmessung bei einer kleineren Cutoff-Frequenzund einer nicht so konservativen Wahl der Cutoff-Ordnungen erreichen, da die Messung derMatsubara-Funktion der dominante Zeitfaktor darstellt. Weiterhin ist es wegen der vorliegendenTeilchen-Loch-Symmetrie möglich den Parameter δ zu verkleinern, ohne dass das Vorzeichen-problem auftritt, wodurch die mittlere Ordnung und die Breite der Verteilung der Ordnungenkleiner wird. Folglich sind die Matrizen, deren Determinanten zu bestimmen sind, im Mittelkleiner und die Rechnungen verlaufen somit schneller.

Nachdem der Verlauf der Doppelbesetzung als Funktion der Wechselwirkungsstärke und dergroße statistische Fehler der Daten diskutiert wurde, verbleibt eine Beurteilung der Ergebnissedurch Vergleich mit anderen Resultaten.Es zeigt sich, dass die T=0-Doppelbesetzung in Abbildung 5.6 (unten) über der aus der VCA/wcCT-WL stammenden Doppelbesetzung liegen. Zwar wurde von E. Gull et al. [82] die Temperatu-rabhängigkeit der Doppelbesetzung untersucht, aber jedoch nur für zwei spezielle Wechselwir-kungsstärken. Dabei stellten sie fest, dass die Doppelbesetzung bei U mit sinkender Temperaturabnimmt. In Abbildung 5.6 (unten) zeigt sich im Vergleich mit den T=0-Daten weitestgehendgenau das entgegengesetzte Verhalten. Allerdings liegen im Wesentlichen nur die Daten desT=0-Koexistenzbereichs vor, so dass um U = 5 die T=0.5-Doppelbesetzung der Plakette überder des T=0-Isolator liegt, jedoch deutlich unter der des T=0-Metalls.Weiterhin zeigt Abbildung 5.6 auch Daten für ein Referenzsystem bestehend aus einem wech-selwirkenden Platz (Nc = 1) und einem Badplatz (nb = 1). Für kleine Wechselwirkungsstärken

84


Abbildung 5.8: Lokale Matsubara-Funktion eines korrelierten Platzes (Nc = 1) mit angebundenen Badplatz(nb = 1) bei T = 0.5. Bei fester Anzahl der Messungen (105 pro Diagrammordnung) weistωn ċ ImGiiiωn stärkeres Rauschen für sehr kleine Hybridisierungsstärken auf.

unterscheiden sich die Doppelbesetzungen aus den Rechnungen mit den beiden Referenzsys-temen kaum, da dort die antiferromagnetischen Korrelationen eine geringe Bedeutung haben.Mit zunehmender Wechselwirkungsstärke nimmt deren Bedeutung zu, wodurch sich die Dop-pelbesetzungen der beiden Referenzsysteme immer mehr unterscheiden. Die kritische Wechsel-wirkungsstärke der Ein-Platz-Approximation ist bekanntermaßen wesentlich größer (vgl. DIA:UcT = 0 11 [24]). In Abbildung 5.6 (unten) ist somit für dieses Referenzsystem eine starkmetallische Lösung zu sehen. Durch das stärkere Hopping des Metalls wird auch eine größereDoppelbesetzung realisiert im Vergleich zu der Plakette, deren Doppelbesetzung bereits denAnfang des Crossover-Bereichs widerspiegelt. Für sehr große Wechselwirkungsstärken sollte derUnterschied zwischen der Cluster- und der Impurity-Doppelbesetzung wieder verschwinden, dadann die Elektronen sehr stark lokalisiert sind und damit das fehlende Hopping nicht so sehrins Gewicht fällt.Wird zusätzlich noch die aus der DCA resultierende Doppelbesetzung aus Ref. [82] für U = 5und T = 0.5 betrachtet (Abbildung 5.6 unten), so fällt auf, dass diese unwesentlich über demVCA/wcCT-WL-Resultat liegt. Dies ist allerdings erwartungsgemäß: In der DCA führt dieErhaltung der Translationsinvarianz durch Benutzung von periodischen Randbedingungen zueiner Doppelzählung des Intraclusterhoppings bei einem 22-Cluster. Durch die Überschätzungder kinetischen Energie werden die Gitterplätze folglich öfter doppelt besetzt sein. Dieser Effektsollte für größere Cluster wesentlich kleiner werden, so dass dann das DCA-Ergebnis wenigerstark von dem VCA-Resultat unterscheiden sollte. Weiterhin zeichnet sich die DCA durch eineEinbettung der Clusterplätze in ein kontinuierliches Bad aus. Es hat sich gezeigt [84], dass dieHinzunahme von weiteren Badplätzen zu einer geringfügig höheren Doppelbesetzung führt.

Aus den beiden Temperatur-Grenzfällen (T=0 und T=0.5) lässt sich ein mögliches Szenario für

85


das Temperaturverhalten der Doppelbesetzung als Funktion der Wechselwirkungsstärke kon-struieren:

Abbildung 5.9: Szenario der Temperaturentwicklung der Doppelbesetzung `de = `ninie als Funktion derWechselwirkungsstärke U : (a) Hochtemperturverlauf (T ª), (b) Verlauf der Doppelbe-setzung leicht oberhalb der kritischen Temperatur Tc, (c) Verlauf unterhalb der kritischenTemperatur

Wie man Abbildung 5.6(unten) entnehmen kann, lässt sich für sehr große Temperaturen dasMetall nicht wesentlich anhand des Verlaufs der Doppelbesetzung als Funktion der Wechsel-wirkungsstärke von dem Isolator unterscheiden (Abbildung 5.9a), da die Wendestelle, die derkritischen Wechselwirkungsstärke UcT des kontinuierlichen Crossovers entspricht, schwierigzu identifizieren ist. Mit sinkender Temperatur verbiegt sich der Verlauf der Doppelbesetzung(Abbildung 5.9b) und die beiden Lösungen beginnen sich zu immer mehr zu unterscheiden. Dadie Steigung an der Wendestelle ausgeprägter ist, lässt sich die Lage von UcT besser bestim-men. Wird die Temperatur unter die kritische Temperatur Tc des Mott-Übergangs abgesenkt(Abbildung 5.9c), so weisen die metallische und die isolierende Lösung einen völlig unterschied-lichen Verlauf der Doppelbesetzung auf, die keine stetige Funktion mehr ist. Es zeigt sich eineHystere und somit ist der Übergang diskontinuierlich.

Abbildung 5.10: Mögliches Szenario für die Temperaturentwicklung der optimalen Hybridisierungsstärke Voptin Abhängigkeit von der Wechselwirkungsstärke U .

Auch für die optimale Hybridisierungsstärke lässt sich ein Szenario für das Temperaturverhal-ten aus den Abbildungen 5.2 und 5.5, die das SFT-Funktion für den Temperaturnullpunkt bzw.den Hochtemperaturlimes zeigen, ableiten: Abbildung 5.10 stellt die optimale Hybridierungs-stärke Vopt in Abhängigkeit von der Wechselwirkungsstärke U für verschiedene Temperaturen

86


dar. Für sehr große Temperaturen ist der Verlauf für alle U nahezu linear, was den geringenUnterschied zwischen dem Metall und dem Isolator charakterisiert. Mit sinkender Temperatur,also zunehmender inverser Temperatur β, verbiegt sich der Verlauf bei kleinen U zu größerenHybridisierungen. Bei der kritischen Temperatur Tc ist zu erwarten, dass es um Uc zu einemnahezu senkrechten Verlauf der optimalen Hybridisierung in Abbildung 5.10 kommt. Unterhalbder kritischen Temperatur treten drei unterschiedliche Lösungen auf, von der eine metastabilist. Diese Lösung wird in 5.10 durch einen parabelförmigen schattierten Bereich gekennzeich-net. Insgesamt ist aufgrund der stärkeren Itineranz der Elektronen mit sinkender Temperaturein Anwachsen der optimalen Hybridisierungsstärke zu erwarten. Für sehr starke Wechselwir-kungen (U ª) sollte jedoch aufgrund der starken Lokalisierung der Elektronen kaum einUnterschied in der optimalen Hybridisierungsstärke, die nun sehr kleine Werte annimmt, zubeobachten sein.

87

6 Fazit und Ausblick

Festkörper sind mikroskopisch gesehen sehr große Gebilde, die durch Gittermodelle mit einerVielzahl von Plätzen beschrieben werden können. Ein besonderes Interesse liegt insbesondereauf den stark korrelierten Elektronensystemen. Diese weisen unter anderem einen wechselwir-kungsgetriebenen Übergang von einem Metall zu einem Isolator auf: den Mott-Übergang. EineUntersuchung von solch großen Systemen ist allerdings nicht effektiv möglich, da das zu lösendeProblem zu komplex ist. Daher wurden Quanten-Cluster-Methoden entwickelt, die die Kom-plexität des Originalsystems auf Cluster zurückführen. Eine solche Methode ist die in Kapitel3 vorgestellte Variational Cluster Approximation (VCA). Bislang wurden die Cluster für dieseMethode mit Exakter Diagonalisierung oder mit der Lanczos-Methode gelöst. Aufgrund des ex-ponentiellen Anwachsens des Rechenaufwands mit der Clustergröße, sind diese Cluster-Solverjedoch nur auf wenige Plätze beschränkt. Um aber eine möglichst gute Approximation durch dieVCA zu erreichen, sollten möglichst große Cluster benutzt werden. Für endliche Temperaturenbieten Quanten-Monte-Carlo-Methoden die Möglichkeit auch weitaus größere Cluster zu lösen,da der Rechenaufwand bei diesen in einem Potenzgesetz skaliert, sofern das Vorzeichenpro-blem nicht auftritt. Allerdings ist die Anwendung von konventionellen Quanten-Monte-Carlo-Methoden als VCA-Cluster-Solver nicht möglich, da diese das für die VCA essentielle großka-nonische Potential des Clusters nicht liefern können. Daher wurde in dieser Arbeit mit demWang-Landau-Algorithmus (Abschnitt 4.3) ein alternativer stochastischer Ansatz vorgestellt,der mit einer diagrammatischen Quanten-Monte-Carlo-Methode für Fermionen kombiniert wur-de, nämlich der weak-coupling Continous Time Quantum Monte Carlo-Methode (Abschnitt 4.2)oder auch kurz wcCT-QMC. In Analogie zu dieser Abkürzung wurde in dieser Arbeit der neuestochastische Cluster-Solver, der sowohl wie Monte-Carlo-Methoden Cluster-Erwartungswerteals auch das großkanonische Potential des Clusters berechnen kann, als wcCT-WL bezeichnet.

Um den wcCT-WL-Algorithmus als VCA-Cluster-Solver zu testen, wurde als Originalsystemdas zweidimensionale Ein-Band-Hubbard-Modell gewählt, das als eins der Standardmodelle fürstark korrelierte Elektronensysteme gilt.Weil der Rechenaufwand beim wcCT-WL-Algorithmus im Wesentlichen der gleiche ist wie beidem zugrunde liegenden Monte-Carlo-Algorithmus, skaliert dieser ebenfalls kubisch in der Clus-tergröße, in der inversen Temperatur und in dem Erwartungswert der potentiellen Energie.Folglich wurde für den Test der Kombination VCA/wcCT-WL nur ein kleiner 2 2-Cluster beieiner inversen Temperatur β = 2 und moderaten Wechselwirkungsstärken (3 B U B 6) gewählt.Dies ermöglichte bei dieser Temperatur die Studie des Crossovers von einem Metall zu einemIsolator (Abschnitt 5.4), der mit dem Mott-Übergang in Verbindung gebracht werden kann.Dazu wurden das großkanonische Potential, die Doppelbesetzung und die Matsubara-Funktionin Abhängigkeit der Wechselwirkungsstärke U betrachtet. Hier zeigte sich die große Stärkedes neuen Cluster-Solvers: wcCT-WL bietet die Möglichkeit, ohne wesentlichen MehraufwandResultate als Funktionen der Wechselwirkungsstärke zu liefern. Dies ist ein erheblicher Vor-teil gegenüber den Quanten-Monte-Carlo-Methoden, die Größen jeweils nur für eine bestimmteWechselwirkungsstärke bestimmen können.Es hat sich gezeigt, dass die Kombination VCA/wcCT-WL für den Hochtemperatur-Crossoverbei β = 2 eine kritische Wechselwirkungsstärke Uc 5.9 in guter Übereinstimmung mit den

89

6 Fazit und Ausblick

Ergebnissen von M. Vekic und S.R. White [87] liefert. Auch ist die Doppelbesetzung bei U = 5von vergleichbarer Größe wie die aus DCA-Rechnungen von E. Gull et al. [82].

Da die Studie des Hochtemperatur-Crossovers mit der VCA/wcCT-WL ähnliche Ergebnisse lie-ferte wie andere Cluster-Methoden, verbleibt es die Effizienz der neuen Methode im Vergleich zuden konkurrierenden Methoden, wie die cellular Dynamical Mean Field Theory (cDMFT) oderder Dynamical Cluster Approximation (DCA) jeweils mit einem Quanten-Monte-Carlo-Cluster-Solver, zu diskutieren. Die VCA weist für die Cluster einen deutlich kleineren Parameterraumauf als ihre Konkurrenten, weshalb die Parameteroptimierung in der VCA schneller abläuft.Die VCA liefert zwar schlechtere Näherungen, aber es hat sich in der Praxis gezeigt, dass dieUnterschiede nur marginal sind. Eine Untersuchung der Performance der einzelnen Cluster-Methoden mit stochastischem Solver wäre daher interessant, um festzustellen, wie groß dermögliche Vorteil der VCA/wcCT-WL sein könnte, insbesondere für Größen als Funktion derWechselwirkungsstärke.

Das zweidimensionale Hubbard-Modell liefert noch weitere Einsatzmöglichkeiten für VCA/wcCT-WL von großem Interesse:Insbesondere lässt sich das Phasendiagramm des Mott-Übergangs untersuchen und die für diecDMFT und DCA unzugängliche Phasentrennlinie UcT bestimmen.Durch die Möglichkeit wesentlich größere Cluster benutzen zu können, werden auch Studien vonGrößen in Abhängigkeit von der Clustergröße Nc möglich. Die Untersuchung der antiferroma-gnetischen Ordnungstemperatur TN stellt dabei für die Quanten-Cluster-Methoden ein bedeut-sames Beispiel dar. Für zweidimensionale Systeme sagt das Mermin-Wagner-Theorem voraus,dass die wahre Néel-Temperatur verschwindet, also TN = 0. Endliche Ordnungstemperaturensind demnach als aus dem Molekularfeldcharakter der Quanten-Cluster-Methoden resultieren-des Artefakt zu deuten. Mit zunehmender Clustergröße sollte jedoch die Néel-Temperatur gegenNull abfallen. Eine vergleichbare Arbeit veröffentlichten M. Jarrell et al. [90] für die DCA.

Weiterhin sind auch die Vorläufer der antiferromagnetischen Phase bei höheren Temperatu-ren von Interesse. Das Inerscheinungtreten von antiferromagnetischen Korrelationen auf kur-zen Zeit- und Längenskalen wird durch einen Pseudogap in der Spektraldichte signalisiert,der ein Vorläufer des antiferromagnetischen Gaps darstellt. Dies wurde von A. Kampf undJ.R. Schrieffer [86] durch einen phänomenologischen Ansatz basierend auf starken antiferro-magnetischen Spinfluktuationen vorausgesagt und von M. Vekic und S.R. White [87] mittelsQuanten-Monte-Carlo-Simulationen endlicher Cluster bestätigt. Außerdem untersuchten M. Ve-kic und S.R. White die Temperatur T , bei sich der Pseudogap bildet, in Abhängigkeit von derWechselwirkungsstärke U für verschiedene Clustergrößen. Eine solche Untersuchung ist nun mitVCA/wcCT-WL möglich. Die Informationen über die Gap-Bildung im halbgefüllten zweidimen-sionalen Hubbard-Modell lassen sich dabei sehr einfach aus der lokalen Matsubara-Funktion inder Zeitdarstellung ablesen [82].

Die hier vorgestellten Anregungen liefern nur einen kleinen Ausschnitt aus den neuen Mög-lichkeiten, die sich durch die Kombination von VCA mit einem stochastischen Cluster-Solverergeben. Durch die Möglichkeit von Studien bei endlichen Temperaturen stellt VCA/wcCT-WLeine sinnvolle Ergänzung zu den T=0-Rechnungen mit VCA/Lanczos dar.

90

A Berechnung der SpektralmomenteAn dieser Stelle soll nun die Berechnung der Spektralmomente, die für die Hochfrequenzent-wicklung der Matsubara-Funktion benötigt werden, für die ersten beiden Ordnungen vorgestelltwerden.Für das nullte Moment der Spektraldichte ergibt sich für den allgemeinen Vielteilchen-Hamiltonian(2.2.2) trivialerweise:

M1αβ = `cα, c†

βe = δαβ .

Durch die Anwendung des Operators L, der das Bilden des Kommutators mit dem gesamtenHamiltonian beinhaltet, wird bereits die Berechnung des Spektralmoments erster Ordnung et-was komplizierter.Zunächst wird das Spektralmoment M

1αβ in einen freien und in einen Wechselwirkungsanteil

aufgespalten:M1αβ = `cα,H , c†

βe = `cα,H0 , c†βe + `cα,H1 , c†

βe .Mit dem Kommutator

cα,H0 = cα,Qij

tijc†icj =Q

ij

tij cα, c†icj =Q

ij

tijδαicj =Qj

tαjcj

folgt für den freien Anteil des Spektralmoments:

`cα,H0 , c†βe = `Q

j

tαjcj , c†βe =Q

j

tαjcj , c†β =Q

j

tαjδjβ = tαβ .

Wendet man sich nun dem Wechselwirkungsanteil zu, so ist zunächst der entsprechende Kom-mutator zu berechnen:

cα,H1 = cα,1~2 Qα′β′γ′δ′

Uα′β′δ′γ′c†α′c

†β′cγ′cδ′

=12Q

α′β′γ′δ′Uα′β′δ′γ′ cα, c†

α′c†β′cγ′cδ′

=12Q

α′β′γ′δ′Uα′β′δ′γ′ δαα′c

†β′cγ′cδ′ − δαβ′c

†α′cγ′cδ′

=12Q

β′γ′δ′Uαβ′δ′γ′c

†β′cγ′cδ′ −

12Uα′αδ′γ′c

†α′cγ′cδ′

Mit dem Antikommutator c†αcγcδ, c

†β = δβδc

†αcγ − δβγc†

αcδ folgt nun:

cα,H1 , c†β =

12Qβ′γ′

Uαβ′βγ′c†β′cγ′ −

12Qβ′δ′

Uαβ′δ′βc†β′cδ′ −

12Qα′γ′

Uα′αβγ′c†α′cγ′

+

12Qα′δ′

Uα′αδ′βc†β′cδ′

=12Qij

Uαiβj +Uiαjβ −Uαijβ −Uiαβj c†icj

= Qij

Uαiβj −Uαijβ c†icj

91

A Berechnung der Spektralmomente

und somit für den Wechselwirkungsanteil von M1αβ :

`cα,H1 , c†βe = Q

ij

Uαiβj −Uαijβ `c†icje .

Insgesamt ergibt sich also für das erste Moment der Spektraldichte:

M1αβ = tαβ +Q

ij

Uαiβj −Uiαβj `c†icje.

92

B Beweise

B.1 Beweis von Formel (2.1.5)

Zu beweisen:

`Ae = ∂Ω∂λ

für H =H′ + λA

Beweis:

∂Ω∂λ

= −

1β

∂

∂λlnΞ = −

1β

1Ξ

tr∂

∂λe−βH

′+λA

= = −1β

1Ξ

trª

Qk=0

−βkk!

∂

∂λH′ + λAk

= −

1β

1Ξ

trª

Qk=0

−βkk!

k

Qr=1

Hk−rAHr−1

= −

1β

1Ξ

trª

Qk=0

−βkk!

kHk−1A

= −

1β

1Ξ

trª

Qk=0

−βk−1k − 1!H

k−1−βA

= −

1β

1Ξ−β trAe−βH

= `Ae

B.2 Beweis von Formel (4.2.11)

`ke = 1Ξ~Ξ0

`Sβ,0 ke0

=1

Ξ~Ξ0

ª

Qk=0

−1kk!

kSβ

0dτ1...dτk `T H1τ1...H1τke0

=1

Ξ~Ξ0

ª

Ql=0

−1l+1l + 1! l + 1S

β

0dτ1...dτl dτl+1 `T H1τ1...H1τlH1τl+1e0

93

B Beweise

= −

1Ξ~Ξ0

ª

Ql=0

−1ll! S

β

0dτ1...dτl dτ `T H1τ1...H1τlH1τe0

= −

1Ξ~Ξ0

Sβ

0dτª

Ql=0

−1ll! S

β

0dτ1...dτl `T H1τ1...H1τlH1τe0

= −Sβ

0dτ

1Ξ~Ξ0

`T Sβ,0H1τe0

= −Sβ

0dτ `H1τe

= −β `H1e

B.3 Beweis von Formel (4.2.12)Analog zu B.2 ergibt sich

ak2f = Sβ

0dτ dτ ′ `T H1τH1τ ′e − S

β

0`H1τe

= β Sβ

0dτ `T H1τH10e − β `H1e .

Aus

∂Ω∂U=

1U`H1e und

∂2Ω∂U2

=∂

∂U

1U`H1e = − 1

U2S

β

0dτ `T H1τH10e − β `H1e2

folgt

ak2f = β2 `H1e2 + β `H1e − βU∂ `H1e

∂U− β `H1e

= β2 `H1e2 − βU∂ `H1e

∂U.

Die daraus resultierende Varianz ist dann:

∆2k = ak − `ke2f = ak2f − `ke2

= β2 `H1e2 − βU∂ `H1e

∂U− β2 `H1e2

= −βU∂ `H1e

∂U.

Wird nun der Operator D = Pi di = Pi nini eingeführt, so lässt sich der Erwartungswertder Hubbard-Wechselwirkung in symmetrischer Form bei fester Füllung im Wesentlichen alsSumme der erwarteten Doppelbesetzungen der einzelnen Gitterplätze interpretieren, also H1 =

U Pi di + U ċ const. = UD + U ċ const. Insbesondere gilt bei translationsinvarianten Systemenmit L Plätzen `die = `de und somit `De = L `de. Damit ist die Varianz der Verteilung derDiagrammordnungen mit der Doppelbesetzung verknüpft:

∆2k = −βU `De − βU2 ∂ `De∂U

+U ċ const.

= −βUL `de − βU2L∂ `de∂U

+U ċ const.

94

B.4 Fouriertransformation von (4.2.34)

B.4 Fouriertransformation von (4.2.34)

gCkii′σ iω = S

β

0dτ g

Ckii′σ τ eiωτ

= G0ii′σiω − S

β

0dτ eiωτ

k

Qr,s=1

G0iri′στr − τ ′D−1rsσCkG0iisστ − τsUτ ′=0

= G0ii′σiω − S

β

0dτ eiωτ 1

βS

β

0dτ0

k

Qr,s=1

G0iri′στr − τ0D−1rsσCkG0iisστ + τ0 − τs

= G0ii′σiω −

1β3 Q

ω′ω′′S

β

0dτ S

β

0dτ0 eiωτ e−iω

′τr−τ0 e−iω′′τ+τ0−τs

ċ

ċ

k

Qr,s=1

G0iri′σiω′D−1rsσCkG0iisσiω′′

= G0ii′σiω −

1βQ

ω′ω′′δω′ω′′δωω′′e

−iω′τreiω′′τs

k

Qr,s=1

G0iri′σiω′D−1rsσCkG0iisσiω′′

= G0ii′σiω −

1β

k

Qr,s=1

G0iri′σiω eiωτsD−1rsσCke−iωτrG0iisσiω.

95

B Beweise

96

C Schätzung von Fittingparametern

Die von A.M. Legendre (1806) und C.F. Gauß (1809) unabhängig voneinander entwickelte Me-thode der kleinsten Quadrate stellt ein sehr häufig benutztes Prinzip zur Parameterschätzungdar. In dieser Methode wird die mittlere quadratische Abweichung einer Stichprobe von einerparameterisierten Funktion minimiert, um die Funktion an die Daten anzufitten.Sei nun vorausgesetzt, dass die Daten x1, y1, ..., xN , yN unabhängig und identisch nor-malverteilte Fehler besitzen und die Werte y1, ..., yN über eine durch den Vektor a paramete-risierte Funktion fa von den Werten x1, ..., xN abhängen, dann ist die mittlere quadratischeAbweichung ea der Funktionswerte fax1, ..., faxN von den Werten y1, ..., yN gegebendurch:

ea =1N

N

Qi=1

yi − faxi2 . (C.1)

Um nun die mittlere quadratische Abweichung ea zu minimieren, muss der Gradient dieserbezüglich dem Parametervektor a verschwinden:

∂ea

∂a= 0 . (C.2)

Diese Bedingung führt auf ein Gleichungsystem, in dem die Komponenten des k-dimensionalenParametervektors a = a1, ..., ak im Allgemeinen abhängig voneinander sind. Die gesuchtenSchätzer der einzelnen Komponenten a1, ..., ak ergeben sich dann durch Lösen des Gleichungs-systems.

In Abschnitt 3.4 wurde die Möglichkeit der Extrapolation der Frequenzsummanden des nieder-frequenten Anteils vom SFT-Funktional vorgeschlagen, damit der Hochfrequenzanteil (3.4.8)weitestgehend unabhängig von der Cutoff-Frequenz ωc wird. Aus der in (3.4.10) gewonnendenErkenntnis, dass die einzelnen Summanden im Niederfrequenzanteil (3.4.3) wie ω−2n abfallen,lässt sich somit ein quadratischer Abfall gemäß α ω−2n an die ermittelten Daten anfitten. Dabeikann die Bestimmung des Parameters α über die Methode der kleinsten Quadrate erfolgen. Umdie Statistik für die Parameterschätzung zu verbessern, empfiehlt es sich, auch relativ kleineFrequenzen mitzuberücksichtigen. Allerdings läuft man in die Gefahr, dass der quadratischeAbfall der Frequenzsummanden noch nicht vorliegt. Daher sollten noch weitere Ordungen derHochfrequenzentwicklung mitgenommen werden. So lässt sich zeigen, dass der Abfall der Fre-quenzsummanden nur mit geraden Exponenten geschieht. Daher ist eine für den Fit geeigneteFunktion gegeben durch:

fx = α

x2+

β

x4. (C.3)

Folglich ist dann die zu minimierende mittlere quadratische Abweichung:

eαβ =1N

N

Qi=1

yi −α

x2i

+

β

x4i

2

. (C.4)

97

C Schätzung von Fittingparametern

Das Bilden der partiellen Ableitung nach dem Parameter α ergibt mit der Forderung des Ver-schwindens von dieser:

∂eαβ

∂α= −

2N

N

Qi=1

1x2

i

yi −α

x2i

+

β

x4i

!= 0

α =PN

i=1yi

x2i− βPN

i=11x6

i

PNi=1

1x4

i

. (C.5)

Analog erhält man für den Parameter β:

β =PN

i=1yi

x4i− αPN

i=11x6

i

Pi=1 N 1x4

i

(C.6)

Dieses aus den Gleichungen (C.5) und (C.6) gebildete Gleichungssystem ist noch zu lösen undergibt letztlich für die Schätzer der Fittingparameter:

α =a1b2 − a2b1

a3b2 − a22

, (C.7)

β =b1 − a2α

b2(C.8)

mit den Abkürzungen

a1 =

N

Qi=1

yi

x2i

, a2 =

N

Qi=1

1x6

i

, a3 =

N

Qi=1

1x4

i

,

b1 =

N

Qi=1

yi

x4i

, b2 =

N

Qi=1

1x8

i

.

Neben der Methode der kleinsten Quadrate wird auch oft die Maximum-Likelihood-Methodefür die Schätzung von Parametern verwendet. Diese liefert Schätzer mit minimaler Varianz. DieMaximum-Likelihood-Schätzer für den Fit an die Daten für die Frequenzsummanden sollen nunkurz vorgstellt werden. Für eine allgemeine Diskussion der Maximum-Likelihood-Methode seiauf [34] verwiesen.

Um die Schätzer für den Fit an die Frequenzsummanden des niederfrequenten Anteils des SFT-Funktionals mit der Maximum-Likelihood-Methode zu konstruieren, wird die zur Funktion fxgehörende log-Likelihood-Funktion

L =N

Qi=1

lnyi −a

x2i

−

β

x4i

nach den Parameter α und β partiell abgeleitet und die resultierenden Ableitungen gleich Nullgesetzt. Wie bei der Methode der kleinsten Quadrate ergibt sich ein Gleichungssystem für dieParameter:

α =1N

N

Qi=1

yix2i −

β

x2i

,

β =1N

N

Qi=1

yix4i − αx2

i .

98

Durch Lösung dieses Gleichungssystems erhält man die folgenden Parameterschätzer:

αML =a − bc

1 − bd, (C.9)

βML = c − αd (C.10)

mit den Abkürzungen

a =1N

N

Qi=1

yix2i , b =

1N

N

Qi=1

1x2

i

, c =1N

N

Qi=1

yix4i , d =

1N

N

Qi=1

x2i .

Die Maximum-Likelihood-Schätzer sind somit weniger komplex als die Schätzer aus der Methodeder kleinsten Quadrate und daher auch numerisch robuster.

99

Literaturverzeichnis

[1] W. NOLTING, Grundkurs Theoretische Physik 6 - Statistische Physik, Sprin-ger, Berlin (2007)

[2] W. NOLTING, Grundkurs Theoretische Physik 7 - Viel-Teilchen-Theorie,Springer, Berlin (2005)

[3] G. CZYCHOLL, Theoretische Festkörperphysik: Von den klassischen Model-len zu modernen Forschungsthemen, Springer, Berlin (2008)

[4] A.A. ABRIKOSOV, L.P. GORKOV und I.E. DZYALOSHINSKI, Methods ofQuantum Field Theory in Statistical Physics, Dover Publications, New York(1975)

[5] A.L. FETTER und J.D. WALECKA, Quantum Theory of Many-ParticleSystems, McGraw-Hill, New York (1971)

[6] J.W. NEGELE und H. ORLAND, Quantum Many-Particle Systems,Addison-Wesley, Redwood City (1988)

[7] M. POTTHOFF, Anwendungen der Vielteilchentheorie in der Festkörperphy-sik, Vorlesungsskript, Humboldt-Universität zu Berlin (1999)

[8] F. BLOCH, Z. Phys. 52, 555 (1929)

[9] J.G. BEDNORZ und K.A. MÜLLER, Z. Phys. B 64, 189 (1986)K.A. MÜLLER und J.G. BEDNORZ, Science 237, 1133 (1987)

[10] J. HUBBARD, Proc. Roy. Soc. London A 276, 238 (1963)

[11] J. KANAMORI, Prog. Theor. Phys. 30, 275 (1963)

[12] M.C. GUTZWILLER, Phys. Rev. Lett. 10, 159 (1963)

[13] T. MAIER et al., Phys. Rev. Lett. 85, 1524 (2000)

[14] E.H. LIEB und F.Y. WU, Phys. Rev. Lett. 20, 1445 (1968)

[15] H. TASAKI, J. Phys.: Condens. Matter 10, 4353 (1998)

[16] E.H. LIEB Phys. Rev. Lett. 62, 1201 (1989)

[17] G.-S. TIAN J. Phys. A: Math. Gen. 25, 109 (1992)

[18] R.O. ZAITSEV und Y.V. MIKHAILOVA, Low Temp. Phys. 22, 974 (1996)

[19] A. MIELKE, Starke Korrelationen und Magnetismus, Vorlesungskript, Uni-versität Heidelberg (2008)

101


[20] L.D. LANDAU, Phys. Z. Sowjetunion 11, 26 (1937)L.D. LANDAU, Zh. Eksp. Teor. Fiz. 7, 19 (1937)

[21] J.M. LUTTINGER und J.C. WARD, Phys. Rev. 118, 1417 (1960)

[22] G. BAYM und L.P. KADANOFF, Phys. Rev. 124, 287 (1961)

[23] M. POTTHOFF, Condens. Mat. Phys. 9, 557 (2006)

[24] M. POTTHOFF, Eur. Phys. J. B 32, 429 (2003)

[25] M. POTTHOFF, M. AICHHORN und C. DAHNKEN, Phys. Rev. Lett. 91,206402 (2003)

[26] M. POTTHOFF, Eur. Phys. J. B 36, 335 (2003)

[27] C. DAHNKEN et al., Phys. Rev. B 70, 245110 (2004)

[28] M. POTTHOFF, Adv. in Solid State Phys. 45, 135 (2005)

[29] M. POTTHOFF, Systematics of approximations constructed from dynamicalvariational principlesin: Effective models for low-dimensional strongly correlated electrons, Hrsg.:G. Batrouni and D. Poilblanc, S. 41, AIP Proceedings, Melville (2006)

[30] M. POTTHOFF, Phys. Rev. B 75, 125112 (2007)

[31] M. BALZER, W. HANKE und M. POTTHOFF, Phys. Rev. B 77, 045133

[32] A.H. NEVIDOMSKYY, D. SÉNÉCHAL und A.-M.S. TREMBLAY, Phys.Rev. B 77, 075105 (2008)

[33] W.H. Press et al., Numerical Recipes - The Art of Scientific Computing,Camebridge University Press, New York (2007)

[34] W. VON DER LINDEN und A. PRÜLL, Wahrscheinlichkeitstheorie, Statistikund Datenanlyse, Vorlesungsskript, TU Graz (2007)

[35] D. MEINTRUP und S. SCHÄFFLER, Stochastik - Theorie und Anwendun-gen, Springer, Berlin (2005)

[36] W. FELLER, An Introduction to Probability Theory and Its Applications -Vol. I, Wiley, New York (1968)

[37] H. DADUNA, Stochastische Prozesse I, Vorlesungsskript, Universität Ham-burg (2007)

[38] V. SCHMIDT, Markov-Ketten und Monte-Carlo-Simulation, Vorlesungs-skript, Universität Ulm (2003)

[39] N. METROPOLIS et al., J. Chem. Phys. 21, 1087 (1953)

[40] W.K. HASTINGS, Biometrika 57(1), 97 (1970)

[41] M.E.J. NEWMAN, G.T. BARKEMA, Monte Carlo Methods in StatisticalPhysics, Oxford University Press, New York (1999)

102


[42] D.P. LANDAU und K. BINDER, A Guide to Monte Carlo Simulations inStatistical Physics, Cambridge University Press, Cambridge (2005)

[43] V.I. MANOUSIOUTHAKIS und M.W. DEEM, J. Chem. Phys. 110, 2753(1999)

[44] D. FRENKEL, PNAS 101, 17571 (2004)

[45] B.A. BERG, Markov Chain Monte Carlo Simulations and Their StatisticalAnalysis, World Scientific, Singapore (2004)

[46] A.D. SOKAL, Monte Carlo Methods in Statistical Mechanics: Foundationsand New Algorithmsin: Functional Integration (Cargèse, 1996),NATO Adv. Sci. Inst. Ser. B Phys. 361, 131, New York (1997)

[47] N.V. PROKOFEV, B.V. SVISTUNOV und I.S. TUPITSYN, JETP Letters64, 911 (1996)

[48] A.N. RUBTSOV und A.I. LICHTENSTEIN, JETP Letters 80, 61 (2004),A.N. RUBTSOV, V.V. SAVKIN und A.I. LICHTENSTEIN, Phys. Rev. B72, 035122 (2005)

[49] M. JARRELL, A. MACRIDIN, und K. MIKELSONS, The Dynamical Clus-ter Approximation with Quantum Monte Carlo Cluster Solvers,in: Lectures on the Physics of Strongly Correlated Systems XII, AIP Procee-dings (2008)

[50] F.F. ASSAAD und T.C. LANG, Phys. Rev. B 76, 035116 (2007)

[51] E. GULL et al., Phys. Rev. B 76, 235123 (2007)

[52] M. TROYER und U.-J. WIESE, Phys. Rev. Lett. 94 170201 (2005)

[53] E. GORELOV, Electronic structure of multiorbital correlated systems, Dis-sertation, Universität Hamburg (2007)

[54] P. WERNER, Diagrammatic Monte Carlo simulation of quantum impuri-ty models - weak and stron coupling approach, Vorlesungsskript, ColumbiaUniversity, New York (2008)

[55] K. HAULE, Phys. Rev. B 75, 155113 (2007)

[56] F. WANG und D.P. LANDAU, Phys. Rev. Lett. 86, 2050 (2001)F. WANG und D.P. LANDAU, Phys. Rev. E 86, 2050 (2001)

[57] B.J. SCHULZ et al., Phys. Rev. E 67, 067102 (2003)

[58] M. TROYER et al., Phys. Rev. Lett. 90, 120201 (2003)

[59] C. ZHOU und R.N. BHATT, Phys. Rev. E 72, 025701(R) (2005)

[60] H.K. LEE, Y. OKABE und D.P. LANDAU, Comp. Phys. Commun. 175, 36(2006)

[61] A.N. MOROZOV und S.H. LIN, Phys. Rev. E 76, 0267601 (2007)

103


[62] R.E. BELARDINELLI und V.D. PEREYRA, J. Chem. Phys. 127, 184105(2007)R.E. BELARDINELLI und V.D. PEREYRA, Phys. Rev. E 75, 046701 (2007)

[63] E. LANGE, Mod. Phys. Lett. B 12, 915 (1998)

[64] E. DAGOTTO, Rev. Mod. Phys. 66, 763 (1994)

[65] P. WEISS, J. Phys. Radium 6, 661 (1907)

[66] W. METZNER und D. VOLLHARDT, Phys. Rev. Lett. 62, 324 (1989)

[67] E. MÜLLER-HARTMANN, Z. Phys. B: Condens. Matter 74, 507 (1989)

[68] G. KOTLIAR und D. VOLLHARDT, Physics Today 57, 53 (2004)

[69] M.H. HETTLER et al., Phys. Rev. B 58, R7475 (1998)

[70] G. KOTLIAR et al., Phys. Rev. Lett. 87, 186401 (2001)

[71] C. GROS und R. VALENTI, Phys. Rev. B 48, 418 (1993)

[72] D. SÉNÉCHAL et al., Phys. Rev. Lett. 84, 522 (2000)

[73] D. SÉNÉCHAL, An introduction to quantum cluster methods, ar-Xiv:0806.2690v1 [cond-mat.str-el] (2008)

[74] A. GEORGES et al., Rev. Mod. Phys. 68, 13 (1996)

[75] T. MAIER et al., Rev. Mod. Phys. 77, 1027 (2005)

[76] N.F. MOTT, Proc. R. Soc. London A 62, 416 (1949)

[77] N.F. MOTT, Metal-Insulator Transitions, Taylor and Francis, London (1990)

[78] F. GEBHARD, The Mott Metal-Insulator Transition, Springer, Berlin (1997)

[79] M. POTTHOFF, Correlated electrons at metal surfaces, Habilitationsschrift,Humboldt-Universität zu Berlin (1999)

[80] N. BLÜMER, Mott-Hubbard Metal-Insulator Transition and Optical Conduc-tivity in High Dimensions, Dissertation, Universität Augsburg (2002)

[81] H. PARK, K. HAULE und G. KOTLIAR, Phys. Rev. Lett 101, 186403 (2008)

[82] E. GULL et al., EPL 84, 37009 (2008)

[83] M. BALZER et al., EPL 85, 17002 (2009)

[84] M. BALZER, Persönliche Mitteilung mit Datensätzen von VCA/Lanczos-Rechnungen für 2 2-Cluster mit je einem und je zwei Badplätze pro korre-liertem Platz bei T = 0.

[85] A.H. NEVIDOMSKYY et al., Phys. Rev. B 77, 064427 (2008)

[86] A. KAMPF und J.R. SCHRIEFFER, Phys. Rev. B 41, 6399 (1990)

[87] M. VEKIC und S.R. WHITE, Phys. Rev. B 47, 1160 (1993)

104


[88] C. HUSCROFT et al., Phys. Rev. Lett. 86, 139 (2001)

[89] K. HAULE und G. KOTLIAR, Phys. Rev. B 76, 104509 (2007)

[90] M. JARRELL et al., Phys. Rev. B 64, 195130 (2001)

[91] M. ECKSTEIN, The frustrated Hubbard model on the Bethe lattice - an inves-tigation using the self-energy functional approach, Diplomarbeit, UniversitätAugsburg (2006)

105

Eidesstattliche ErklärungHiermit erkläre ich an Eides statt, dass ich die vorliegende Diplomarbeit zum Thema

„Variational Cluster Approximation mit stochastischem Cluster-Solver“

selbstständig und ohne fremde Hilfe angefertigt habe. Ich habe dabei nur die in der Arbeitangegebenen Quellen und Hilfsmittel benutzt.

Hamburg, den 28.01.2009

EinverständniserklärungHiermit erkläre ich mein Einverständnis zur Ausleihe der vorliegenden Diplomarbeit durch dieBibliotheken der Universität Hamburg.

Hamburg, den 28.01.2009

Diplomarbeit - theorie.physnet.uni-hamburg.de · Er unterscheidet sich von einem Molekül vor allem...

Documents

Transcript of Diplomarbeit - theorie.physnet.uni-hamburg.de · Er unterscheidet sich von einem Molekül vor allem...