8/17/2019 Dinamik Programming

1/31

Electrical Power

System OperationUnit Commitment (part 2)

Week#6

8/17/2019 Dinamik Programming

2/31

Unit Commitment Solution

MethodsDynamic programmingchief advantage over enumeration schemes is

the reduction in the dimensionality of theproblem  in a strict priority order scheme there are only N

combinations to try for an N unit system

 a strict priority list !ould result in a

theoretically correct dispatch and commitmentonly if   the no"load costs are ero  unit input"output characteristics are linear

 there are no other limits constraints or restrictions  start"up costs are a $%ed amoun

8/17/2019 Dinamik Programming

3/31

Unit Commitment Solution

Methods Dynamic programming  the follo!ing assumptions are made in this

implementation of the D& approach

 a state consists of an array of units  !ith speci$ed units operating and the rest decommitted (o'"line)  a feasible state is one in !hich the committed units can supply

the reuired load and meets the minimum capacity for each period

 start"up costs are independent of the o'"line or do!n"time

 ie it is a $%ed amount !rt time  no unit shutting"do!n costs  a strict priority order !ill be used !ithin each interval  a speci$ed minimum amount of capacity must be

operating !ithin each interval

8/17/2019 Dinamik Programming

4/31

Unit Commitment Solution

Methods *he for!ard D& approach  runs for!ard in time from the initial hour to the $nal hour  the problem could run from the $nal hour back to the initial

hour  the for!ard approach can handle a unit+s start"up costs that

are a function of the time it has been o'"line (temperaturedependent)  the for!ard approach can readily account for the system+s history

 initial conditions are easier to speci$ed !hen going for!ard

 the minimum cost function for hour K !ith combination I,-cost(./)0min1&cost Fcost(K,I)=min[Pcost(K,I)]+Scost(K-1,L:K,I)+Fcost(K-1.L)]

345  F cost(K  I) 0 least total cost to arrive at state (K  I)  Pcost(K  I) 0 production cost for state (K  I)

 Scost(K 7 L, K  I) 0 transition cost from state (K 7 L) to (K  I)

8/17/2019 Dinamik Programming

5/31

Unit Commitment Solution

Methods *he for!ard D& approach  state (K  I) is the Ith commitment combination in hour K   a strategy is the transition or path from one state at a

given hour to a state at the ne%t hour    is de$ned as the number of states to search each period  N is de$ned as the number of strategies to be saved at each

step  these variable allo! control of the computational e'ort  for complete enumeration the ma%imum value of  or N is 2N  7

 for a simple priority"list ordering the upper bound on 8 is n thenumber of units  reducing N means that information is discarded about the

highest cost schedules at each interval and saving only thelo!est N paths or strategies  there is no assurance that the theoretical optimum !ill be found

8/17/2019 Dinamik Programming

6/31

Unit Commitment SolutionMethods  *he for!ard D& approach

 restricted search paths  9 0 :  8 0 ;

8/17/2019 Dinamik Programming

7/31

Unit Commitment Solution

Methods  hour load

patternUnit Pmax Pmin IncrementalHeat Rate

No-loadCost

Full-load Ave. Cost

Min. Time(h

(M! (M! ("tu # $!h (% # h (% # m!h U& 'on

) *+ , )++ ,)/.++ ,/. ,

, ,+ 0+ 1+++ *.0, ,+./ /

/ /++ 2 *2/+ 0*.2 )1.2

0+ ,+ ))1++ ,,.++ ,*.++ ) )

Unit

InitialCondition

o33(- #on(4(h

5tart-u& Costs

Hot (% Cold(% Cold start(%

3 8 500 1100 5

4 -6 0 0.02 0

 Hour 6oad (M!

1 450

2 530

3 600

4 540

5 400

6 280

7 290

8 500

8/17/2019 Dinamik Programming

8/31

Unit Commitment SolutionMethods

8/17/2019 Dinamik Programming

9/31

Unit Commitment SolutionMethods  Case 7, ?trict priority"list ordering

 the only states e%amined each hour consist of the listed four,  state ;, unit : state 72, : @ 2 state 7=, : @ 2 @ 7 state 7;, all four

 all possible commitments start from state 72 (initial condition)  minimum unit up and do!n times are ignored  in hour 7,

 possible states that meet load demand (=;A BW), 72 7= 7;5tate Unit 5tatus Ca&acit7

5 0010 300 MW

12 0110 550 MW

14 1110 630 MW

15 1111 690 MW

Pcost()8) 9F)(,4F,()+4F/(/++4F)(, :conomic 'is&atch :;.9)2/./04,+.**(,4)*()+4)2.0(/++4,/.*+(,+91*0)./0

Fcost()8)9Pcost()8)45cost(+8),

8/17/2019 Dinamik Programming

10/31

Unit Commitment SolutionMethods Case 7 in hour 7,  minimum at state 72 (2A>)

 in hour 2,  possible states that meet load demand (;:A BW), 72

7= 7;

 ? Pcost 5cost Fcost

15 9861 350 10211

14 9493 350 9843

12 9208 0 9208

cos 1 2 3 1

cos cos cos

(2,15) (25) (185) (300) (20)

1735 2088(25) 18(185) 17046(300) 2380(20) 11301

(2,15) (2,15) (1, : 2,15)

350 9208

11301 min 0 9843 208

0 10211

t 

t t t 

 P F F F F 

 F P S L

 DP state transition equation

= + +

= + + + + =

= +

− − −

+ = + + =

+

59

8/17/2019 Dinamik Programming

11/31

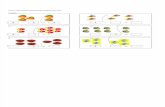
Unit Commitment Solution

Methods  Case 7, D& diagram  total cost, E:=:

 priority order list up"times and do!n"times neglected

8/17/2019 Dinamik Programming

12/31

Unit Commitment Solution

Methods Case 2, complete enumeration (2;6 F 7A

possibilities)  fortunately most are not feasible because they do not

supply suGcient capacity

 in this case the true optimal commitment isfound  the only di'erence in the t!o traHectories occurs in

hour : it is less e%pensive to turn on the less eGcient peaking unit

#= for three hours than to start up the more eGcient unit#7 for that same time period

 only minor improvement to the total cost  case 7, E:=:

8/17/2019 Dinamik Programming

13/31

Unit Commitment Solution

Methods Case 2, D& diagram

8/17/2019 Dinamik Programming

14/31

Unit Commitment Solution

Methods 4agrange Iela%ation dual variables and dual optimiation  consider the classical constrained optimiation

problem  primal problem, minimie ! ( " 7J "n) subHect to K( " 7

J "n) 0 A  the 4agrangian function, L( " 7J "n) 0 ! ( " 7J "n) @ L

K( " 7J "n)  de$ne a dual function

 then the Mdual problemN is to $nd  the solution involves t!o separate optimiation

problems in the case of conve% functions this rocedure is

1 2

1 2,

( ) min ( , , ) x x

q L x xλ λ =

*

0( ) max ( )q q

λ 

λ λ ≥

=

8/17/2019 Dinamik Programming

15/31

Unit Commitment Solution

Methods 

8/17/2019 Dinamik Programming

16/31

Unit Commitment Solution

Methods /terative form of 4agrange rela%ation

methodthe optimiation may contain non"linear or non"

conve% functionsiterative process based on incremental

improvements of L is reuired to solve theproblem select a arbitrary starting L

solve the dual problem such that #(L) becomes larger update L using a gradient adHustment,

$nd closeness to the solution by comparing the gapbet!een the MprimalN function and the dual function

primal function, $O 0 min L relative duality gap, in practice the gap

( )t t    dq

d 

λ λ λ α 

λ 

= +

* *

*

( ) j q

q

−

8/17/2019 Dinamik Programming

17/31

Unit Commitment Solution

Methods 4agrange rela%ation for unit commitmentloading constraint

unit limits

unit minimum up"time and do!n time

constraintsthe obHective function

1

0

1....

 N t t t 

load i i

i

 P P U 

t T 

=

− =

∇ =

∑

min max

1.... & 1....

t t t 

i i i i iU P P U P  

i N t T  

≤ ≤

∇ = =

... ,

1 1

( ) ( )T N 

t t t t  

i i start up i t i i i

t i

 F P S U F P U −= =

+ + = ∑∑

8/17/2019 Dinamik Programming

18/31

Unit Commitment Solution

Methods -ormation of the 4agrange function  in a similar !ay to the economic dispatch problem

 unit commitment reuires that the minimiation of the4agrange function subHect to all the constraints  the cost function and the unit constraints are each separated

over the set of units  !hat is done !ith one unit does not a'ect the cost of running

another unit as far as the cost function unit limits and the up"timeand do!n"time constraints are concerned

 the loading constraint is a coupling constraint across all theunits

 the 4agrange rela%ation procedure solves the unit

commitment by temporarily ignoring the couplingconstrain

1 1

( , , ) ( , )T N 

t t t t t  

i i i i i

t i

 L P U F P U P P U λ λ 

= =

= + −

∑ ∑

8/17/2019 Dinamik Programming

19/31

Unit Commitment Solution

Methods *he dual procedure attempts to reach the

constrainedoptimum by ma%imiing the4agrangian !ith respect to the4agrange multiplier

done in t!o basic steps ?tep 7, $nd a value for each lt !hich moves #(L)

to!ards a larger value ?tep 2, assuming that Lt found in ?tep 7 is $%ed $nd

the minimum of L by adHusting the values of Pt and %t minimiing L

*

,

( ) max ( )... ... ( ) min ( , ,)t t t 

i i P U 

q q where q L P U  λ 

λ λ λ λ  = =

, ,1 1 1 1 1

( )T N T T N  

t t t t t t  

i t i i t i load i it i t t i

 L F P S U P P U λ λ = = = = =

= + + − ∑∑ ∑ ∑∑

8/17/2019 Dinamik Programming

20/31

Unit Commitment SolutionMethodsseparation of the units from one anotherP the

inside term can

no! be solved independently for each generating

unit the minimum of the 4agrangian is found bysolving for the minimum for each

generating unit over all time periodssubHect to the up"time and do!n"time constraints andthis is easily solved as a t!ostate dynamic programming

problem of one variable

,

1

( )T 

t t t t  

i i i t i i i

t 

 F P S U P U λ =

+ − ∑

,

1 1

min ( ) min {[ ( ) ] } N T 

t t t t t  

i i i t i i i

i i

q F P S U P U  λ λ = =

= + −∑ ∑min max

1...

t t t 

i t i i t  U P P U P  

t T 

≤ ≤

∀ =

8/17/2019 Dinamik Programming

21/31

Unit Commitment SolutionMethodsMinimizing the function with respect

to Pitat the Uit 0 A state the minimiation is trivial and

euals ero

at the Uit 0 7 state the minimiation !rt is,

there are three cases to be considered for &iopt andthe limits

min[ ( ) ]

[ ( ) ] [ ( )]

0

t t 

i i i

t t 

t i i i i i

t t i i

 F P P 

d F P P d F P  

dP dP  

λ 

λ λ 

+

+

= + =

min min min

min max

max max max

[ ( ) ] [ ( ) ]

[ ( ) ] [ ( ) ]

[ ( ) ] [ ( ) ]

opt t t t  

i i i i i i i i

opt t t opt t opt  

i i i i i i i i i

opt t t t  

i i i i i i i i

 fP P ThenMin F P P F P P 

ifP P P ThenMin F P P F P P  

ifP P ThenMin F P P F P P  

λ λ 

λ λ 

λ λ 

≤ − = −

≤ ≤ − = −

≤ − = −

[ ( ) ] 0t i i i F P P λ − <

8/17/2019 Dinamik Programming

22/31

Unit Commitment Solution

Methods QdHusting L L must be carefully adHusted to ma%imie (L) various techniues use a mi%ture of heuristic strategies

and gradient search methods to achieve a rapid

solution Lt for the unit commitment problem L is a vector of Lt +s to

be adHusted each hour

 simple techniue

 gradient component, !here

 heuristic component,

( )t t    dq

d 

λ λ λ α 

λ 

= +

1

( )t    N 

t t t 

load i i

i

dq P P U 

d 

λ 

λ    =

= − ∑( )

0.01 ~ ~

( )

0.01 ~ ~

dqwhen IsPositive

d 

dq

when IsNegatif    d 

λ α 

λ 

λ 

α  λ 

=

=

8/17/2019 Dinamik Programming

23/31

Unit Commitment Solution

Methods *he relative duality gap used as a measure of the closeness to the solution  for large real"sie po!er"systems unit"commitment

calculations the duality gap becomes uite small as thedual optimiation proceeds  the larger the commitment problem the smaller the gap

 the convergence is unstable at the end  some units are being s!itched in and out

 the process never comes to a de$nite end  there is no guarantee that !hen the dual solution process

stops it !ill be at a feasible solution

 the gap euation,  * *

*

( ) J q

q

−

8/17/2019 Dinamik Programming

24/31

Unit Commitment Solution

Methods4agrange rela%ation algorithm using dual

optimiation

8/17/2019 Dinamik Programming

25/31

Unit Commitment Solution

Methods 

8/17/2019 Dinamik Programming

26/31

Unit Commitment SolutionMethods /teration 7,(L)0AARO0=AAAA (RO"O)SO0unde$ned

 /teration 2,

 dynamic programming for unit #:

 Hour U) U, U/ P) P, P/ ';(# &)edc &,edc &/edc

1 0 0 0 0 0 0 0 170 0 0 0

2 0 0 0 0 0 0 0 520 0 0 0

3 0 0 0 0 0 0 0 1100 0 0 0

4 0 0 0 0 0 0 0 330 0 0 0

8/17/2019 Dinamik Programming

27/31

Unit Commitment Solution

Methods /teration 2,(L)07=>2 RO0=AAAA (RO"O)SO076E

 Hour U) U, U/ P) P, P/ ';(#

&)ed

c &,edc &/edc

1 1.7 0 0 0 0 0 0 170 0 0 0

2 5.2 0 0 0 0 0 0 520 0 0 0

3 11 0 1 1 0 400 200 500 0 0 0

4 3.3 0 0 0 0 0 0 330 0 0 0

8/17/2019 Dinamik Programming

28/31

Unit Commitment Solution

Methods /teration :,(L)07>:== RO0:6A2= (RO"O)SO0A6;

 Hour U) U, U/ P) P, P/ ';(#

&)ed

c

&,ed

c

&/ed

c1 3.4 0 0 0 0 0 0 170 0 0 0

2 10.4 0 1 1 0 400 200 -80 0 320 200

3 16 1 1 1 600 400 200 -100 500 400 200

4 6.6 0 0 0 0 0 0 330 0 0 0

8/17/2019 Dinamik Programming

29/31

Unit Commitment Solution

Methods /teration =,(L)0727= RO02>A6 (RO"O)SO0A;A2

 Hour U) U, U/ P) P, P/ ';(# &)edc &,edc &/edc

1 5.1 0 0 0 0 0 0 170 0 0 0

2 10.24 0 1 1 0 400 200 -80 0 320 200

3 15.8 1 1 1 600 400 200 -100 500 400 200

4 9.9 0 1 1 0 380 200 -250 0 130 200

8/17/2019 Dinamik Programming

30/31

Unit Commitment Solution

Methods /teration ;,(L)07;:2 RO0:6A2= (RO"O)SO0A>==

 Hour U) U, U/ P) P, P/ ';(# &)edc &,edc &/edc

1 6.8 0 0 0 0 0 0 170 0 0 0

2 10.08 0 1 1 0 400 200 -80 0 320 200

3 15.6 1 1 1 600 400 200 -100 500 400 200

4 9.4 0 0 1 0 0 200 130 0 0 200

8/17/2019 Dinamik Programming

31/31

Unit Commitment SolutionMethods /teration 6,(L)07==2 RO02A7EA (RO"O)SO0AA:E

 Iemarksthe commitment schedule does not change signi$cantly

!ith further iterationsh th l ti i t t bl ( ill ti f it 2)

 Hour U) U, U/ P) P, P/ ';(# &)edc &,edc &/edc

1 8.5 0 0 1 0 0 200 -30 0 0 170

2 9.92 0 1 1 0 384 200 -64 0 320 200

3 15.4 1 1 1 600 400 200 -100 500 400 200

4 10.7 0 1 1 0 400 200 -270 0 130 200