Capıtulo 3

Linealizacion por realimentacion

3.1. Introduccion

La linealizacion por realimentacion es un metodo de diseno de sistemas de control

no lineales que ha experimentado gran auge y aceptacion en los ultimos anos. La

idea principal es la de transformar, de forma parcial o total, la dinamica no lineal

del sistema a controlar en una dinamica lineal. El hecho de obtener una dinamica

resultante lineal, permite aplicar tecnicas lineales para obtener el sistema en bucle

cerrado deseado. Por otro lado, el principal inconveniente del metodo es que exige

disponer de un modelo exacto del sistema. Para solventar este inconveniente R. Ma-

rino y P. Tomei presentan en [104] un metodo de linealizacion por realimentacion

adaptativo para sistemas con incertidumbres en el modelo. En esta investigacion no

se estudiara el caso de control adaptativo.

Este capıtulo esta dividido en dos bloques principales:

En el primer bloque se van a resumir los conceptos principales referentes a la

linealizacion por realimentacion (A. Isidori [57], S. Sastry [129], J. Slotine [141],

M. Spong [143], R. Su [146], V. Etxebarrıa [35]). Se definiran los conceptos

de grado relativo, linealizacion entrada-estado, linealizacion entrada-salida y

dinamica cero. Se extendera el metodo de linealizacion por realimentacion para

el caso multivariable. Se introducira la definicion de la matriz de desacoplo, que

permite conseguir el desacoplamiento entre las entradas y las salidas, es decir,

un control sin interaccion. Por otro lado, se comentaran los diversos metodos

33

Autor: Manuel Lopez-Martinez.

Curso: MASTER EN AUTOMÁTICA, ROBÓTICA Y TELEMÁTICA. 2009

Capítulo: Linealización por realimentación.Título: Diseño de sistemas no lineales.

34

para intentar obtener grado relativo cuando este no esta bien definido, bien

por extension dinamica o bien por inversion del sistema. Para finalizar con los

preliminares teoricos, se remarcaran los puntos en comun de la linealizacion por

realimentacion con el concepto de flatness ( M. Fliess [38, 39, 40], M. Rathinam

y R. Murray [122, 110, 113, 123]).

En el segundo bloque se presentaran todos los casos de estudio analizados con

linealizacion por realimentacion en esta tesis, haciendo mayor hincapie en las

aportaciones publicadas, ası como en el material original aun sin publicar.

3.2. Preliminares teoricos

La teorıa de la linealizacion por realimentacion se basa en diversos conceptos

matematicos de geometrıa diferencial.

A continuacion se presentan conceptos matematicos como el gradiente de una

funcion escalar, el Jacobiano de una funcion vectorial y la derivada direccional de un

campo escalar en la direccion de un campo vectorial, tambien conocida como derivada

de Lie. Se define, tambien, el concepto de difeomorfismo y se expone el teorema de

Frobenius, el cual se refiere a la existencia de soluciones para sistemas de ecuaciones

en derivadas parciales.

Tras el formalismo matematico, se presentan las tecnicas de linealizacion por rea-

limentacion para sistemas SISO, tanto entrada-estado como entrada-salida. Para los

casos en que un sistema no es completamente linealizable, se presentan tanto el con-

cepto de grado relativo como la representacion de sistemas en su forma normal, la

cual permite descomponer la dinamica total del sistema en dinamica externa lineal

y dinamica interna no lineal. Esta descomposicion sera muy util cuando se pretenda

estudiar la estabilidad de la dinamica interna del sistema, ya sea globalmente, o ya sea

localmente, en cuyo caso se hablara de dinamica cero. El analisis de estabilidad de la

dinamica cero permitira disenar controladores de alta ganancia que aseguren la esta-

bilidad asintotica local del sistema completo. Por ultimo se extenderan los conceptos

expuestos para el caso de sistemas MIMO.

35

3.2.1. Formalismo matematico

A continuacion se expondran algunos conceptos basicos:

Gradiente de una funcion escalar.

Jacobiano de una funcion vectorial.

Si h(x) es una funcion escalar del estado (n-dimensional), su gradiente es un vector

de dimension (1 × n) definido por:

∇h =∂h

∂x=

[∂h

∂x1

· · · ∂h

∂xn

](3.2.1)

Si f(x) es una funcion vectorial del estado (n-dimensional), tambien llamada campo

vectorial, el Jacobiano viene dado por una matriz de dimensiones (n × n)

∇f =∂f

∂x=

⎡⎢⎢⎣

∂f1

∂x1· · · ∂f1

∂xn

.... . .

...∂fn

∂x1· · · ∂fn

∂xn

⎤⎥⎥⎦ (3.2.2)

Definicion 3.2.1. Sea la funcion escalar h : Rn −→ R y el campo vectorial f :

Rn −→ R

n. Se define la derivada de Lie o derivada direccional de h en la direccion

de f como la funcion escalar dada por:

�Lfh = ∇h·f (3.2.3)

Las derivadas direccionales multiples pueden definirse recursivamente segun:

�L0fh = f ; �Li

fh = �Lf

(�Li−1

f h)

= ∇ (�Li−1

f h) ·f i = 1, 2, . . . (3.2.4)

Del mismo modo, si g(x) es otro campo vectorial, entonces la funcion escalar doble

derivada direccional de h respecto de f y g viene dada por:

�Lg�Lfh = ∇(�Lfh)·g (3.2.5)

Este concepto es importante desde el punto de vista de control, porque las derivadas

respecto del tiempo de la salida de un sistema dinamico, ası como la derivada de una

funcion de Lyapunov candidata, pueden expresarse en terminos de derivadas de Lie.

36

Definicion 3.2.2. Sean f y g dos campos vectoriales en Rn. Se define el campo

adjunto de g respecto de f o corchete de Lie como:

adfg = [f , g] = ∇gf −∇fg (3.2.6)

y de forma recursiva

ad0fg = g; adi

fg = [f , adi−1f g] i = 1, 2, . . . (3.2.7)

Difeomorfismos y transformaciones en el espacio de estado

Definicion 3.2.3. Una funcion φ : Rn → R

n definida en una region Ω del espacio de

estado es un difeomorfismo si es suave y su inversa φ−1 existe y es tambien suave.

Si Ω es todo el espacio Rn, entonces φ(x) se denomina difeomorfismo global.

Lema 3.2.1. Sea φ(x) una funcion suave definida en una region Ω de Rn. Si el

Jacobiano ∇φ es no singular en un punto xo de Ω, entonces φ(x) es un difeomorfismo

local en una subregion de Ω.

Los difeomorfismos son transformaciones no lineales que sirven para cambiar las va-

riables de estado en las que se expresa un sistema no lineal.

El Teorema de Frobenius

El teorema de Frobenius se refiere a la existencia de soluciones para sistemas de

ecuaciones en derivadas parciales. Este teorema sera usado en el tratamiento formal

de la linealizacion por realimentacion completa de sistemas de orden n. Antes de

enunciar el teorema de Frobenius es necesario definir que son sistemas completamente

integrables y sistemas involutivos.

Definicion 3.2.4. Se dice que un conjunto linealmente independiente de campos

vectoriales {f1, . . . ,fm} en Rn es completamente integrable si y solo si existen n − m

37

funciones escalares h1(x), h2(x), . . . , hn−m(x), donde x es el estado del sistema, tales

que satisfacen el siguiente sistema de ecuaciones diferenciales en derivadas parciales:

�Lfjhi = ∇hi·fj = 0 1 ≤ i ≤ n − m; 1 ≤ j ≤ m (3.2.8)

y los gradientes ∇hi son linealmente independientes.

Notese que al ser m el numero de campos vectoriales y n la dimension del espacio

asociado, el numero de funciones escalares incognitas hi es n − m, y por tanto el

numero de ecuaciones en derivadas parciales sera el producto del numero de campos

vectoriales por el numero de funciones incognitas, esto es, m(n − m).

Definicion 3.2.5. Se dice que un conjunto de campos vectoriales linealmente inde-

pendientes {f1, . . . ,fm} en Rn es involutivo si y solo si existen funciones escalares

αijk : Rn → R tales que:

[fi,fj](x) =m∑

k=1

αijk(x)fk(x) ∀i, j (3.2.9)

Involutividad significa que si se forman los corchetes de Lie de cualquier par de

campos vectoriales del conjunto {f1, . . . ,fm}, entonces el campo vectorial resultante

puede ser expresado como combinacion lineal del conjunto original de campos vecto-

riales. Notese que:

Los campos vectoriales constantes son siempre involutivos. De hecho, el corchete

de Lie de dos vectores constantes es el vector cero, que puede ser trivialmente

expresado como combinacion lineal de los campos vectoriales.

Un conjunto compuesto de un vector f es involutivo. De hecho,

[f , f ] = (∇f)f − (∇f)f = 0

Visto lo anterior, se puede presentar el teorema de Frobenius.

Teorema 3.2.2. Sea {f1, . . . ,fm} un conjunto de campos vectoriales linealmente

independientes. El conjunto es completamente integrable si y solo si es involutivo.

38

3.2.2. Linealizacion entrada-estado SISO

Definicion 3.2.6. Un sistema SISO no lineal descrito por las ecuaciones

x = f(x) + g(x)u (3.2.10)

se dice que es linealizable entrada - estado si existe una region Ω en Rn, un difeomor-

fismo φ : Ω → Rn y una ley de control no lineal

u = α(x) + β(x)ν (3.2.11)

tales que las nuevas variables de estado z = φ(x) y la nueva entrada ν satisfagan la

relacion lineal invariante en el tiempo siguiente:

z = Az + bν (3.2.12)

donde A y b viene definidos por:

A =

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣

0 1 0 · · · 0

0 0 1 · · · 0

......

.... . .

...

0 0 0 · · · 1

0 0 0 · · · 0

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦

b =

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣

0

0

...

0

1

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦

(3.2.13)

El estado z se denomina estado linealizante, y la ley de control u = α(x) + β(x)ν

se denomina ley de control linealizante.

El siguiente teorema establece las condiciones necesarias y suficientes para que un

sistema del tipo x = f(x) + g(x)u pueda linealizarse entrada-estado.

Teorema 3.2.3. El sistema no lineal x = f(x) + g(x)u, donde f(x) y g(x) son

campos vectoriales suaves, es linealizable entrada-estado si y solo si existe una region

Ω tal que se cumplen las dos siguientes condiciones:

39

Los campos vectoriales {g, adfg, . . . , adn−1f g} son linealmente independientes en

Ω.

El conjunto {g, adfg, . . . , adn−2f g} es involutivo en Ω.

La primera condicion representa una condicion de controlabilidad generalizada

para sistemas no lineales afines en la actuacion.

Observacion 3.2.1. Un sistema no lineal puede ser controlable aunque su aproximacion

lineal no lo sea.

La segunda condicion es siempre satisfecha por los sistema lineales, por lo que

puede establecerse el siguiente corolario.

Corolario 3.2.4. Un sistema lineal es linealizable entrada-estado si y solo si es con-

trolable.

Metodo para linealizar entrada-estado

Los pasos para linealizar por realimentacion entrada-estado un sistema no lineal

de la forma x = f(x) + g(x)u son los siguientes:

Construir los campos vectoriales {g, adfg, . . . , adn−1f g} para el sistema dado.

Probar si se cumplen las condiciones de controlabilidad generalizada y la de

involutividad.

Si se cumplen ambas condiciones, encontrar la primera componente del nuevo

vector de estado, z1, resolviendo las ecuaciones:

∇z1·g = ∇z1·adfg = ∇z1·ad2fg = . . . = ∇z1·adn−2

f g = 0 (3.2.14)

∇z1·adn−1f g �= 0 (3.2.15)

Este sistema de ecuaciones es equivalente a resolver el sistema de ecuaciones:

�Lgz1 = �Lg�Lfz1 = . . . = �Lg�Ln−2f z1 = 0 (3.2.16)

�Lg�Ln−1f z1 �= 0 (3.2.17)

40

Calcular el nuevo vector de estado completo a partir de su primera componente

z1, mediante la transformacion

z(x) =[

z1 �Lfz1 . . . �Ln−1f z1

]T

(3.2.18)

y la ley de control linealizante

u = α(x) + β(x)ν

u =ν − �Ln

fz1

�Lg�Ln−1f z1

(3.2.19)

donde:

α(x) =−�Ln

fz1

�Lg�Ln−1f z1

β(x) =1

�Lg�Ln−1f z1

(3.2.20)

Notese, que la resolucion simbolica de sistemas de ecuaciones diferenciales en deri-

vadas parciales, representa un problema complejo de calculo que solo esta parcialmen-

te resuelto. En la actualidad hay programas de calculo avanzado, tales como MAPLE,

que aportan soluciones particulares para algunas clases de sistemas de ecuaciones di-

ferenciales.

3.2.3. Linealizacion entrada-salida SISO

En esta seccion se discutira la linealizacion entrada-salida de sistemas no lineales

con una entrada descritos por la representacion en el espacio de estados

x = f(x) + g(x)u (3.2.21)

y = h(x) (3.2.22)

donde y es la salida del sistema. Por linealizacion entrada-salida se entiende la gene-

racion de una relacion diferencial lineal entre la salida y y una nueva entrada ν.

Generando una relacion lineal entrada-salida

El procedimiento general para obtener dicha ley de linealizacion consiste en derivar

la salida y repetidas veces hasta que aparezca la entrada u, y entonces disenar u para

41

cancelar la no linealidad. El numero de veces que es necesario derivar se conoce por

el nombre de grado relativo.

A continuacion se introducira el concepto formal de grado relativo.

Definicion 3.2.7. El sistema no lineal de una entrada y una salida

x = f(x) + g(x)u

y = h(x)

se dice que tiene grado relativo r en el punto xo si:

1. �Lg�Lkfh(x) = 0 para todo x en un entorno Ωx de xo y todo k < r − 1

2. �Lg�Lr−1f h(x) �= 0

Observacion 3.2.2. Si n es el orden del sistema de partida, siempre se cumplira que

r ≤ n.

Observacion 3.2.3. Si el grado relativo de un sistema x = f(x)+g(x)u respecto a la

salida y = h(x) es r = n, entonces la linealizacion entrada-salida, en virtud de 3.2.16

y tomando z1 = y, es equivalente a la linealizacion entrada-estado.

Del mismo modo se puede enunciar el siguiente lema.

Lema 3.2.5. La linealizacion entrada-estado es resoluble si y solo si existe un entorno

Ωx de xo y una salida h(x) evaluada en R definida en Ωx, tal que el sistema

x = f(x) + g(x)u

y = h(x)

tiene grado relativo n en xo.

42

Observacion 3.2.4. Puede ocurrir que dada una salida determinada el grado relativo

de un sistema no este bien definido para un punto.

A continuacion se estudiara el caso en el que el grado relativo esta bien definido,

y posteriormente el caso en el que no lo este.

Caso I: Grado relativo bien definido

Considerese una region Ωx en el espacio de estado. Si se deriva respecto al tiempo

la salida y, y se utiliza la notacion de derivada direccional (derivada de Lie), se obtiene:

y =∂h

∂xx = ∇h·(f + gu) = �Lfh(x) + �Lgh(x)u (3.2.23)

Si se verifica que �Lgh(x) �= 0 para algun x = xo, entonces por continuidad, la relacion

se verifica en un entorno finito Ω de xo. En esta region, la transformacion de la entrada

definida por:

u =ν − �Lfh

�Lgh(3.2.24)

da lugar a la relacion lineal y = ν. Sin embargo, si �Lgh(x) = 0, ∀x ∈ Ωx, entonces

no puede construirse la anterior transformacion, y hay que derivar la salida respecto

del tiempo una vez mas:

y = �L2fh(x) + �Lg�Lfh(x)u (3.2.25)

Si �Lg�Lfh(x) = 0, ∀x ∈ Ωx, se debe seguir derivando la salida, hasta que para algun

entero r se obtenga:

y(r) = �Lrfh(x) + �Lg�Lr−1

f h(x)u (3.2.26)

con �Lg�Lr−1f h(x) �= 0 para algun xo ∈ Ωx. Entonces por continuidad, la relacion

anterior se cumplira tambien en un entorno finito Ω de xo. En esta region Ω, la ley

de control

u =ν − �Lr

fh

�Lg�Lr−1f h

(3.2.27)

da lugar a la relacion lineal-entrada salida

y(r) = ν (3.2.28)

El numero de derivadas necesarias es el grado relativo del sistema como se ha definido

en la definicion 3.2.7.

43

Caso II: Grado relativo no definido

Regresando a la definicion 3.2.7, se observa que puede haber puntos donde el

grado relativo no esta definido. Esto ocurre, de hecho, cuando la primera funcion de

la secuencia

�Lgh(x), �Lg�Lfh(x), . . . , �Lg�Lkfh(x), . . . (3.2.29)

que no sea identicamente cero (en un entorno de xo) tenga un cero exactamente en

el punto x = xo. Sin embargo, el conjunto de puntos donde un grado relativo puede

ser definido es claramente un subconjunto abierto del conjunto Ω donde el sistema

x = f(x) + g(x)u (3.2.30)

y = h(x) (3.2.31)

esta definido.

Observacion 3.2.5. En el caso de que el grado relativo del sistema no este bien definido

para una salida h(x) dada, se puede optar por disenar una nueva salida ficticia de

tal manera que el grado relativo sı este bien definido, al menos localmente en torno

al punto de trabajo elegido.

3.2.4. Formas normales

Un sistema SISO no lineal

x = f(x) + g(x)u (3.2.32)

y = h(x) (3.2.33)

de grado relativo r < n puede transformarse en un sistema parcialmente lineal. El

sistema resultante puede descomponerse en un subsistema lineal de orden r, que

representa la dinamica externa entrada-salida, y en un subsistema no lineal de orden

n− r que representa la dinamica interna de los estados que no afectan a la salida. En

la siguiente proposicion se resumira el concepto de linealizacion parcial.

44

Proposicion 3.2.6. Considerese un sistema no lineal con grado relativo r en un

punto xo. La ley linealizante

u =ν − �Lr

fh(x)

�Lg �Lr−1f h(x)

(3.2.34)

transforma este sistema en un sistema cuyo comportamiento entrada salida es identico

al de un sistema lineal que tenga una funcion de transferencia

H(s) =1

sr(3.2.35)

La descomposicion obtenida se denomina forma normal, la cual puede escribirse

en un sistema SISO con grado relativo r como a continuacion se indica. En primer

lugar se denotara con la letra η al vector correspondiente a los estados que forman la

dinamica externa:

η =[

z1 . . . zr

]T

(3.2.36)

Del mismo modo se denotara con la letra χ al vector correspondiente a los estados

que forman la dinamica interna.

χ =[

zr+1 . . . zn

]T

(3.2.37)

z1 = y = h(x)

z1 = z2

z2 = z3

...

zr−1 = zr

zr = �Lrfz1 + �Lg�Lr−1

f z1u = ν

χ = q(η,χ)

Se supondra a partir de ahora y sin perdida de generalidad, que en el punto de

equilibrio xo los vectores (η, χ) son nulos. Por lo tanto, si xo era un equilibrio para

45

el sistema en las coordenadas originales, su correspondiente punto (η, χ) = (0, 0)

es un punto de equilibrio para el sistema en las nuevas coordenadas. Al linealizar

parcialmente el sistema e imponer un controlador externo ν que lleve los estados de

la dinamica externa asintoticamente a cero, no se esta garantizando que el estado

completo del sistema llegue de forma asintotica al equilibrio xo. Para que esto ocurra,

es necesario que los estados de la dinamica interna del sistema tambien tiendan de

forma asintotica a cero. En general, demostrar esto no es una tarea sencilla, siendo

necesario atacar el problema de otra forma. Se plantean dos opciones: estabilizacion

asintotica global o estabilizacion asintotica local.

Estabilizacion asintotica global

Como se ha comentado anteriormente, el analisis de la estabilidad de la dinamica

interna es un problema practicamente intratable en la mayorıa de los casos. En gene-

ral, para hacer frente al diseno de un controlador externo ν que haga que el equilibrio

en cero sea globalmente asintoticamente estable, se tendra que buscar una funcion de

Lyapunov, de tal manera que garantice que tanto los estados de la dinamica externa

como los estados de la dinamica interna converjan de forma asintotica a cero.

Estabilizacion asintotica local

Un metodo sencillo para conseguir la estabilizacion asintotica local consiste en

disenar el controlador externo ν para que estabilice unicamente los estados de la

dinamica externa. Para realizar esto bastarıa disenar un controlador lineal de tal

manera que el polinomio caracterıstico del subsistema externo en bucle cerrado sea

Hurwitz.

zr = �Lrfz1 + �Lg�Lr−1

f z1u = ν

ν = −c1z1 − c2z2 − . . . − crzr

o lo que es lo mismo

y(r) = �Lrfy + �Lg�Lr−1

f yu = ν

ν = −c1y − c2y − . . . − cry(r−1)

46

Para garantizar que el sistema completo sea al menos localmente asintoticamente es-

table, se ha de garantizar que en un entorno del equilibrio (η,χ) = (0, 0), la dinamica

interna tienda tambien de forma asintotica a cero. Esto se puede garantizar analizando

una propiedad intrınseca del sistema

x = f(x) + g(x)u (3.2.38)

y = h(x) (3.2.39)

denominada dinamica cero.

Definicion 3.2.8. Se define la dinamica cero como la dinamica interna cuando la

salida y todas sus derivadas son nulas.

Observacion 3.2.6. Para garantizar que las salidas y sus derivadas, es decir, los estados

de la dinamica externa, tiendan de forma asintotica a cero, se ha de cumplir que la

dinamica cero del sistema sea asintoticamente estable.

Definicion 3.2.9. Se define sistema de fase mınima como aquel cuya dinamica cero

es asintoticamente estable. Analogamente, se define sistema de fase no mınima como

aquel cuya dinamica cero es inestable.

A continuacion se estudiara el problema de hacer identicamente cero la salida (Ze-

roing the Output). Este consiste en encontrar el par formado por dos valores iniciales,

uno correspondiente al valor inicial del estado interno, χo, y el otro, el correspondien-

te al valor inicial de la ley de control linealizante, uo, de tal manera que la salida del

sistema y sus derivadas, es decir los estados de la dinamica externa, permanezcan a

cero para todo instante t en un entorno de t = 0. Haciendo cero los estados externos

en (3.2.38), se obtiene:

η = 0

�Lrfh(x(t)) + �Lg�Lr−1

f h(x(t))u(t) = 0

u(t) =−�Lr

fh(x(t))

�Lg�Lr−1f h(x(t))

(3.2.40)

χ(t) = q(0,χ(t)), χ(0) = χo

47

donde u(t) esta evaluado para η = 0, y sustituyendo la condicion inicial χ(0) = χo

se obtiene uo. Notese que esta senal de control linealizante es la unica entrada capaz

de mantener la salida identicamente a cero para todos los instantes de tiempo.

Observacion 3.2.7. Si al analizar la dinamica cero, esta resulta asintoticamente esta-

ble, la senal de control linealizante tendera de forma asintotica a cero. Por lo tanto,

si la dinamica externa tambien es asintoticamente estable, entonces la dinamica com-

pleta es localmente asintoticamente estable (LAS).

Se acaba de mostrar un metodo para disenar un controlador que haga que un

equilibrio sea localmente asintoticamente estable (LAS). Este metodo es mas potente

que el consistente en realizar un aproximacion lineal del sistema en torno a un punto y

disenar un controlador local. Esto es ası porque el metodo expuesto permitira demos-

trar la estabilidad para casos en los que el sistema linealizado tenga autovalores con

parte real nula y sea marginalmente estable. A este tipo de problemas se le denomina

Problemas Crıticos de Estabilizacion Asintotica Local, y la nocion de dinamica cero

es muy util ya que permite demostrar la estabilidad local del sistema.

Observacion 3.2.8. Este metodo permite estabilizar sistemas cuya aproximacion lineal

contenga modos incontrolables correspondientes a autovalores sobre el eje imaginario.

Permite resolver problemas crıticos de estabilizacion asintotica local buscando una

salida ficticia de tal manera que su dinamica cero sea asintoticamente estable.

3.2.5. Realimentacion con alta ganancia

Este metodo esta muy relacionado tanto con el concepto de dinamica cero, como

con el tratamiento de sistemas singularmente perturbados, los cuales seran tratados

en el capıtulo 5. Este metodo permite disenar controladores para conseguir que el

equilibrio del sistema sea localmente asintoticamente estable (LAS). El controlador

sera lineal y solo realimentara los estados de la dinamica externa, dada por la salida y

sus derivadas. El controlador tendra que tener alta ganancia y no habra necesidad de

realizar linealizacion por realimentacion. Este controlador estabilizara local y asintoti-

camente el estado completo del sistema en el equilibrio si y solo si la dinamica cero

48

del sistema es asintoticamente estable. Se resumira el diseno de estos controladores

en varias proposiciones.

Proposicion 3.2.7. Considerese un sistema de la forma:

x = f(x) + g(x)u

y = h(x)

con f(0) = 0 y h(0) = 0. Supongase que este sistema tiene grado relativo r = 1

en x = 0, y supongase que la dinamica cero del sistema es asintoticamente estable

teniendo ademas todos los autovalores de su Jacobiano en (η,χ) = (0, 0) parte real

negativa. Considerese el sistema en bucle cerrado

x = f(x) + g(x)u

u = −Kh(x) (3.2.41)⎧⎪⎨⎪⎩

K > 0 si �Lgh(0) > 0

K < 0 si �Lgh(0) < 0

⎫⎪⎬⎪⎭ (3.2.42)

Entonces, existe un numero positivo Ko tal que para todo valor de K que satisfaga

que |K| > Ko el equilibrio x = 0 del sistema es asintoticamente estable.

Para el caso en el que el grado relativo es r > 1 se establece la siguiente observa-

cion.

Observacion 3.2.9. Si el grado relativo es r > 1 el problema se puede resolver redu-

ciendose el caso a un sistema de grado relativo r=1. Para ello, se tomara una nueva

salida ficticia w.

w = k(x) = �L(r−1)f h(x) + cr−2 �L

(r−2)f h(x) + . . . + c1 �L

(1)f h(x) + c0h(x) (3.2.43)

o lo que es lo mismo

w = y(r−1) + cr−2y(r−2) + . . . + c1y + c0y

49

donde se ha de cumplir que el polinomio caracterıstico

0 = sr−1 + cr−2sr−2 + . . . + c1s + c0

sea Hurwitz para asegurar que la dinamica cero sea asintoticamente estable. Entonces

el nuevo sistema dado por

x = f(x) + g(x)u

u = −Kk(x) (3.2.44)

tiene grado relativo r = 1 y su dinamica cero es asintoticamente estable. Aplicando

el resultado de la proposicion anterior, existe un numero positivo Ko tal que para

todo valor de K que satisfaga que |K| > Ko el equilibrio x = 0 del sistema es

asintoticamente estable.

3.2.6. Linealizacion por realimentacion MIMO

Al igual que en el caso SISO, se denominara linealizacion entrada-estado cuando

sea posible realizar una linealizacion por realimentacion exacta. En este caso una

linealizacion entrada-salida con la misma eleccion de la salidas dara lugar a que la

dinamica cero es trivial, coincidiendo el orden del sistema con la suma de los grados

relativos parciales de cada una de las salidas (grado relativo total). En el caso de que

no sea posible linealizar el sistema de forma exacta, una linealizacion entrada-salida

permitira linealizar parcialmente la dinamica. La dinamica linealizada se denomina

dinamica externa y sus estados son los que afectan a la relacion entrada-salida. La

dinamica no lineal residual se denomina dinamica interna y esta formada por los

estados que no afectan a la salida. A continuacion se definira el concepto de grado

relativo para el caso de sistemas MIMO.

50

Definicion 3.2.10. Sea el sistema no lineal MIMO dado por las ecuaciones

x = f(x) +m∑

i=1

gi(x)ui (3.2.45)

y1 = h1(x)

...

ym = hm(x)

donde f(x), g1(x), . . . , gm(x) son campos vectoriales suaves, y h1(x), . . . , hm(x) son

funciones suaves definidas en un conjunto abierto de Rn. Se dice que este sistema

tiene grado relativo {r1, . . . , rm} en el punto xo con respecto a las salidas h1(x), . . . ,

hm(x) si:

1. �Lgj�Lk

fhi(x) = 0, para todo 1 ≤ j ≤ m, para todo k < ri−1, para todo 1 ≤ i ≤ m,

y para todo x en un entorno de xo.

2. La matriz m × m

A(x) =

⎡⎢⎢⎢⎢⎢⎢⎢⎣

�Lg1 �Lr1−1f h1(x) . . . �Lgm �Lr1−1

f h1(x)

�Lg1 �Lr2−1f h2(x) . . . �Lgm �Lr2−1

f h2(x)

......

...

�Lg1 �Lrm−1f hm(x) . . . �Lgm �Lrm−1

f hm(x)

⎤⎥⎥⎥⎥⎥⎥⎥⎦

(3.2.46)

es no singular en x = xo.

Observacion 3.2.10. ri representa el grado relativo respecto de la i-esima salida yi(t),

el cual se define como el numero de veces que se ha de derivar yi(t) en t = to para que

aparezca de forma explıcita al menos una componente del vector de entrada u(to).

51

Linealizacion entrada-estado MIMO

Definicion 3.2.11. Un sistema MIMO descrito por las ecuaciones

x = f(x) +m∑

i=1

gi(x)ui

o de forma compacta

x = f(x) + g(x)u (3.2.47)

donde

g(x) = [g1(x), g2(x), . . . , gm(x)]

u = col(u1, . . . , um)

se dice que es linealizable entrada-estado si dado un estado inicial xo existe un entorno

Ω de xo, una transformacion de coordenadas z = Φ(x) definida en Ω, y una ley de

control no lineal expresada en forma compacta

u = α(x) + β(x)ν (3.2.48)

tales que: [∂Φ

∂x(f(x) + g(x)α(x))

]x=Φ−1(z)

= Az (3.2.49)

[∂Φ

∂x(g(x)β(x))

]x=Φ−1(z)

= B (3.2.50)

y que el sistema

z = Az + B (3.2.51)

tenga una matriz de controlabilidad de rango completo.

52

El siguiente teorema establece las condiciones necesarias y suficientes para que di-

cho sistema pueda ser linealizable entrada-estado. Estas condiciones, al igual que para

el caso SISO, pueden ser establecidas en terminos de propiedades de determinadas

distribuciones generadas por campos vectoriales de la forma:

g1(x), . . . , gm(x), adfg1(x), . . . , adfgm(x), . . . , adn−1f g1(x), . . . , adn−1

f gm(x) (3.2.52)

Mas precisamente, si se usa el concepto de subespacio vectorial generado por un con-

junto de vectores1 (Gen), y se denomina

G0 = Gen{g1(x), . . . , gm(x)}G1 = Gen{g1(x), . . . , gm(x), adfg1(x), . . . , adfgm(x)}...

Gi = Gen{adkfgj : 0 ≤ k ≤ i, 1 ≤ j ≤ m}

para i = 0, 1, . . . , n − 1 el teorema puede ser enunciado de la siguiente forma:

Teorema 3.2.8. Sea la matriz g(xo) de rango m (ecuacion (3.2.47)). Entonces, el

sistema no lineal (3.2.47) es linealizable entrada-estado si y solo si existe un entorno

Ω de xo tal que se cumplen las siguientes tres condiciones:

Para cada 0 ≤ i ≤ n− 1, la distribucion Gi tiene dimension constante cerca de

xo.

La distribucion Gn−1 tiene dimension n.

Para cada 0 ≤ i ≤ n − 2, la distribucion Gi es involutiva2.

Metodo para linealizar entrada-estado

Los pasos para linealizar por realimentacion entrada-estado un sistema MIMO no

lineal como el descrito hasta ahora son:

1El subespacio vectorial generado por un conjunto de vectores (Gen) es el conjunto de todas lascombinaciones lineales de los vectores.

2Vease definicion 3.2.5

53

Probar que se cumplan las tres condiciones mencionadas en el teorema anterior.

Encontrar los nuevas primeras m funciones z1(x), ..., zm(x) resolviendo el sistema

de ecuaciones de la forma:

�Lgj�Lk

fzi(x) = 0 para todo 0 ≤ k ≤ ri − 2, 1 ≤ j ≤ m

Comprobar que se cumple la restriccion de que la matriz A(x) es no singular,

tomando hi = zi.

Comprobar que r1 + r2 + . . . + rm = n, es decir, que el grado relativo total 3 es

igual al orden del sistema.

La ley de control linealizante vendra dada por:

u = α(x) + β(x)ν⎡⎢⎢⎢⎢⎢⎣

u1

u2

...

um

⎤⎥⎥⎥⎥⎥⎦ = A−1

⎡⎢⎢⎢⎢⎢⎣

ν1 − �Lr1f z1

ν2 − �Lr2f z2

...

νm − �Lrmf zm

⎤⎥⎥⎥⎥⎥⎦ (3.2.53)

dando lugar a m ecuaciones de la forma:

z(ri)i = νi

Linealizacion entrada-salida MIMO

La linealizacion entrada-salida de sistemas MIMO se obtiene de forma similar al

caso SISO, es decir, derivando las salidas yi hasta que alguna de las componentes

del vector de entradas, ui, aparezca de forma explıcita. El numero de veces que es

necesario derivar cada salida se conoce con el nombre de grado relativo de la salida

ri. El grado relativo de todas las salidas viene dado por el vector {r1, r2, . . . , rm},tal y como se expuso en la definicion 3.2.10. Al igual que en el caso SISO, se puede

establecer el siguiente lema.

3Vease Linealizacion entrada-salida MIMO.

54

Lema 3.2.9. Sea la matriz g(xo) con rango m. Entonces, la linealizacion entrada-

estado es resoluble si y solo si existe un entorno Ω de xo y m funciones de salida

h1, h2, . . . , hm evaluadas en R y definidas en Ω tales que el sistema dado por las ecua-

ciones (3.2.45) tiene grado relativo {r1, r2, . . . , rm} en xo y ademas el grado relativo

total es igual a n, definido como r1 + r2 + . . . + rm = n.

Observacion 3.2.11. Si el grado relativo esta definido y el grado relativo total es

r1 + r2 + . . . + rm = n, entonces se dice que el sistema es linealizable entrada-estado

y tiene dinamica cero trivial. Si por el contrario el grado relativo total es r1 + r2 +

. . . + rm < n existe una dinamica interna y asociada a ella localmente una dinamica

cero no trivial cuya estabilidad debera ser analizada para asegurar que el equilibrio

xo sea asintoticamente estable.

Caso I: Grado relativo bien definido

Asumiendo que ri es el entero mas pequeno tal que al menos una componente, ui,

del vector de entradas aparece en y(ri)i , entonces:

y(ri)i = �Lri

f hi +m∑

j=1

�Lgj�Lri−1

f hiuj (3.2.54)

con �Lgj�Lri−1

f hi �= 0 para al menos un j, en un entorno Ω de xo. Desarrollando este

procedimiento para cada salida yi resulta:⎡⎢⎢⎢⎢⎢⎣

y(r1)1

y(r2)2

...

y(rm)m

⎤⎥⎥⎥⎥⎥⎦ =

⎡⎢⎢⎢⎢⎢⎣

�Lr1f h1(x)

�Lr2f h2(x)

...

�Lrmf hm(x)

⎤⎥⎥⎥⎥⎥⎦ + A(x)

⎡⎢⎢⎢⎢⎢⎣

u1

u2

...

um

⎤⎥⎥⎥⎥⎥⎦ (3.2.55)

donde A(x) es la matriz de desacoplo presentada en la definicion 3.2.10. Asumiendo

que el grado relativo esta bien definido en un entorno Ω de xo, la matriz de desacoplo

55

A(x) es no singular en dicho entorno, pudiendose despejar por tanto las leyes de

control linealizantes dadas por:

⎡⎢⎢⎢⎢⎢⎣

u1

u2

...

um

⎤⎥⎥⎥⎥⎥⎦ = A−1

⎡⎢⎢⎢⎢⎢⎣

ν1 − �Lr1f h1

ν2 − �Lr2f h2

...

νm − �Lrmf hm

⎤⎥⎥⎥⎥⎥⎦ (3.2.56)

dando lugar a m ecuaciones de la forma:

z(ri)i = νi

Caso II: Grado relativo no definido

La linealizacion por realimentacion solo puede ser realizada si la matriz de desa-

coplo A(x) es invertible en un entorno Ω de xo. Dado el procedimiento directo usado

para construir A(x), esta condicion es bastante restrictiva. A continuacion se pre-

sentaran dos metodos para generar una linealizacion por realimentacion cuando la

condicion de no singularidad de la matriz de desacoplo es violada.

La primera tecnica, denominada Extension Dinamica, requiere definir nuevas en-

tradas ficticias como funciones de las derivadas de las entradas originales del sistema,

de tal forma que la correspondiente matriz de desacoplo sea ahora invertible. Las leyes

linealizantes son disenadas basandose en las nuevas entradas, y el valor de las entradas

originales es calculado mediante integracion. Esta ley de linealizacion por realimen-

tacion se denomina Linealizacion por Realimentacion Dinamica, frente a la que no

necesita de extension dinamica, que se denomina Linealizacion por Realimentacion

Estatica.

La segunda tecnica, y al igual que en el caso SISO, consiste en definir nuevas

salidas de tal manera que el grado relativo este bien definido, y por tanto la matriz

de desacoplo sea invertible. Esta tecnica se denomina Inversion del sistema.

En ambos casos, la estabilidad de la dinamica interna, o localmente la estabilidad

de la dinamica cero, tendra que ser verificada para poder asegurar que el equilibrio

xo es asintoticamente estable.

56

Extension dinamica

Bajo ciertas hipotesis es posible modificar un sistema que no tiene grado relativo

definido en un sistema que sı lo tiene. Esto no puede hacerse como hasta ahora

usando una ley de linealizacion estatica, ya que esta propiedad es invariante usando

este tipo de realimentacion. Por ello, se empleara una estructura de realimentacion

que incorpore un conjunto adicional de nuevas variables de estado que en general

dependeran de las senales de control originales, ui, y de las variables de estado del

sistema. En este caso, las variables de las que dependen los nuevos estados se dice

que son endogenas, ya que pertenecen al sistema original. Este tipo de realimentacion

se conoce como linealizacion por realimentacion dinamica mediante transformacion

endogena y se puede modelar por ecuaciones de la forma:

ζ(t) = E(t, u(t), x(t))

ζ(t) = γ(t, x(t), ζ(t)) + δ(t, x(t), ζ(t))ν(t)

u(t) = α(t, x(t), ζ(t)) + β(t, x(t), ζ(t))ν(t)

(3.2.57)

Por simplicidad de notacion, se considerara un sistema con 2 entradas y 2 salidas.

Supongase que la matriz de desacoplo A(x) tiene rango 1. Esto significa, sin perdida

de generalidad, que se puede redefinir el vector de entradas u para que A(x) tenga

una unica columna no nula (por ejemplo a1(x)) y hacer que todas las derivadas de

las salidas con grado relativo definido dependan exclusivamente de la entrada u1. De

esta forma se puede escribir:

[y

(r1)1

y(r2)2

]=

[�Lr1

f h1(x)

�Lr2f h2(x)

]+ A(x)

[u1

u2

]=

[�Lr1

f h1(x)

�Lr2f h2(x)

]+ a1(x)u1 (3.2.58)

Derivando y reemplazando la dinamica del sistema se obtiene la siguiente ecuacion:

[y

(r1+1)1

y(r2+1)2

]= b(x, u1) + A1(x, u1)

[u1

u2

]=

= b(x, ζ1) + A1(x, ζ1)

[ζ1

u2

]= b(x, ζ1) + A1(x, ζ1)

[u1

u2

]

57

Si la nueva matriz A1(x, ζ1) es invertible, entonces el grado relativo del nuevo sistema

esta definido, donde se ha tomado como nuevo estado ζ1 = u1 y como nueva entrada

u1 = ζ1 = u1. La ley de linealizacion tendra la forma[u1

u2

]= A1(x, ζ1)

−1[ν − b(x, ζ1)]

dando lugar a las dos ecuaciones:

y(r1+1)1 = ν1

y(r1+1)2 = ν2

Las leyes externas dadas por ν seran disenadas para colocar los polos de la dinamica

lineal entrada-salida resultante. Observese que u1 debera se obtenida mediante inte-

gracion, por lo que el controlador es dinamico. En el caso de que la matriz A1(x, ζ1)

sea no singular, el procedimiento se puede repetir anadiendo mas integradores.

Inversion del sistema

Esta tecnica involucra definir nuevas salidas de manera que la nueva matriz de

desacoplo sea invertible. Partiendo del mismo punto que en el extension dinamica, se

va a redefinir la entrada para que las ecuaciones del sistema puedan expresarse de la

siguiente forma:[y

(r1)1

y(r2)2

]=

[�Lr1

f h1(x)

�Lr2f h2(x)

]+ A(x)

[u1

u2

]=

[�Lr1

f h1(x)

�Lr2f h2(x)

]+ a1(x)u1 (3.2.59)

Ahora, en vez de derivar y realizar la extension dinamica, se definira una nueva salida

η tal que:

a1(x) = [ a11(x) a12(x) ]T

η = a12(x)y(r1)1 − a11(x)y

(r2)2

Sustituyendo y(r1)1 y y

(r2)2 de la ecuacion (3.2.59) se obtiene:

η = a12(x)�Lr1f h1 + a12(x)a11(x)u1 − a11(x)�Lr2

f h2 − a11(x)a12(x)u1 =

= a12(x)�Lr1f h1 − a11(x)�Lr2

f h2

58

Como puede observarse, la nueva salida no depende de la senal de control u1, con lo

que se puede seguir derivando. De esta forma, teniendo en cuenta que a12(x) y a12(x)

son funciones de x, se obtiene una ecuacion en la que ahora sı aparecen de forma

explıcita las senales de control.

η = γ0(x) + γ1(x)u1 + γ2(x)u2

Si ahora se vuelve a plantear de nuevo el problema tomando como nuevas salidas y1

y η, se obtiene:

[y

(r1)1

η

]=

[�Lr1

f h1(x)

γ0(x)

]+

[e11 0

γ1(x) γ2(x)

] [u1

u2

]=

[�Lr1

f h1(x)

γ0(x)

]+ A2(x)

[u1

u2

]

donde si la matriz

A2(x) =

[e11 0

γ1(x) γ2(x)

]

es invertible, entonces la ley de control linealizante podra ser elegida como:

[u1

u2

]= A−1

2 (x)

[ν1 − �Lr1

f h1(x)

ν2 − γ0(x)

]

dando lugar a 2 ecuaciones de la forma:

y(r1+1)1 = ν1

η = ν2

Las leyes externas dadas por ν seran disenadas para colocar los polos de la dinamica

lineal entrada-salida resultante. En el caso de que la matriz A2(x) sea no singular el

procedimiento se puede repetir para crear nuevas salidas.

3.2.7. Desacoplamiento entrada-salida de sistemas MIMO

El concepto de grado relativo para los sistemas MIMO ha introducido tambien

una nueva matriz A(x) que se denomina matriz de desacoplo. La matriz de desacoplo

59

permitira desacoplar el sistema multivariable en varios sistemas monovariables inde-

pendientes. El problema de control sin interaccion (desacoplamiento entrada-salida)

se plantea formalmente de la siguiente manera:

Sea el sistema no lineal dado por las ecuaciones (3.2.45) se plantea el problema

de encontrar una ley de realimentacion estatica de la forma:

ui = αi(x) +m∑

j=1

βij(x)νj (3.2.60)

definida en un entorno Ω de xo = 0, con αi(xo) = 0, tal que el sistema en bucle cerrado

tenga grado relativo definido en el punto de equilibrio xo y, para cada 1 ≤ i ≤ m, la

salida yi se vea afectada solo por la correspondiente entrada νi.

Proposicion 3.2.10. El problema de control sin interaccion (desacoplamiento entrada-

salida) es resoluble si y solo si la matriz A(xo) es no singular, es decir, si el sistema

tiene grado relativo definido en xo.

Esta seccion finaliza con algunas consideraciones sobre la estabilidad de un sistema

que ha sido desacoplado a traves de una realimentacion estatica.

Observacion 3.2.12. Si la dinamica externa del sistema desacoplado (via realimen-

tacion estatica) es asintoticamente estable, una condicion suficiente, pero en general

no necesaria, para que el sistema sea localmente asintoticamente estable, es que su

dinamica cero tambien sea asintoticamente estable.

3.2.8. Flatness

Se dice que un sistema es plano (flat), si existen funciones de las salidas, llamadas

salidas planas, tales que todos los estados y las entradas se pueden expresar como

funciones analıticas de aquellas y de un numero finito q de sus derivadas respecto al

tiempo. La siguiente definicion expresa formalmente que es un sistema plano.

60

Definicion 3.2.12. Dado un sistema x = f(x, u), con estados x ∈ Rn, y entradas u

∈ Rm, se dice que el sistema es plano si existen salidas η ∈ R

m que dependen de x,

de u y de un numero finito p de sus derivadas respecto al tiempo,

η = Fη(x, u, u, . . . , u(p))

tales que:

x = Fx(η, η, . . . , η(q))

u = Fu(η, η, . . . , η(q))

Observacion 3.2.13. Para el caso de que exista una unica senal de control (m = 1),

ocurre que si el sistema es linealizable entrada-salida y la dinamica cero es trivial,

entonces el sistema es plano (flat) para las salidas elegidas.

Observacion 3.2.14. Si un sistema x = f(x, u) es plano (flat), existe una linealizacion

por realimentacion dinamica usando una transformacion endogena tal que el sistema

en bucle cerrado es difeomorfico a un sistema lineal controlable.

Observacion 3.2.15. Si un sistema es linealizable mediante realimentacion dinamica

usando una transformacion endogena, dando lugar a que la dinamica cero es trivial,

entonces el sistema es plano (flat) para las salidas elegidas.

Seguimiento de trayectorias

Los sistemas planos son utiles en situaciones donde se requiere una generacion de

trayectorias explıcitas, ya que el comportamiento del sistema plano esta determinado

por sus salidas planas. Se pueden disenar trayectorias en el espacio de las salidas

planas y luego transformarlas en senales de entrada apropiadas.

61

3.3. Aplicaciones

En las siguientes secciones se estudiara la posibilidad de linealizar por realimen-

tacion el subsistema de elevacion (dinamica de cabeceo) del equipo de doble rotor. Se

analizara si el sistema es linealizable por realimentacion en funcion de que el modelo de

propulsion posea un termino lineal en velocidad o, por el contrario, sea estrictamente

cuadratico.

Se mostrara que este sistema, para fuerzas de propulsion estrictamente cuadrati-

cas en velocidad, presenta una singularidad cuando la velocidad del rotor se hace cero

por lo que se haran modificaciones a las leyes de control obtenidas. Se presentaran

controladores usando el concepto de linealizacion por realimentacion aproximada pre-

sentado en [51], permitiendo aplicar una ley aproximada en puntos en los que el grado

relativo del sistema no esta definido, y consiguiendo estabilidad asintotica local.

Al final del capıtulo se presentara el estudio de linealizacion por realimentacion del

equipo de doble rotor completo y se analizara si este es linealizable por realimentacion

para las salidas que representan los angulos de cabeceo y de guinada. Se mostrara que,

tanto para modelos lineales de propulsion como para modelos cuadraticos, la linea-

lizacion por realimentacion para las salidas elegidas da lugar a una dinamica cero

asintoticamente estable si y solo si las fuerzas de resistencia (drag) en las helices son

mayores que las de sustentacion (lift). Se analizaran las causas de este efecto y se

aportaran posibles soluciones.

3.4. Dinamica de cabeceo del equipo de doble ro-

tor

En este apartado se mostrara como controlar el subsistema de elevacion del equipo

de doble rotor, considerando que el resto de la dinamica esta desacoplada. Ademas se

estudiaran varios modelos del sistema, considerando modelos de propulsion cuadrati-

cos y lineales, y se aportaran soluciones de control para cada uno de ellos.

Se presenta un controlador compuesto por dos leyes de linealizacion que conmutan

62

al aproximarse a valores bajos de velocidad, en los que la linealizacion por realimen-

tacion con modelo cuadratico no esta bien definida (trabajo publicado en [89]).

Para robustecer el controlador conmutado ante incertidumbre parametrica depen-

diente de la dinamica de los motores, se realiza la linealizacion por realimentacion en

dos pasos. En el primer paso se linealiza por realimentacion el motor y se le aplica un

controlador tal que el motor se comporte como un sistema lineal de primer orden. En

el segundo paso se linealiza por realimentacion la dinamica conjunta del cuerpo y del

motor (trabajo publicado en [87]). Para eliminar la conmutacion en la ley de control

se plantea un modelo de propulsion cuadratico con un termino lineal de constante

muy pequena. Con este modelo se obtiene una ley de control unica aproximada cuya

estabilidad asintotica en el origen es demostrada, presentandose ademas, resultados

experimentales (trabajo publicado en [90]).

En primer lugar se estudiara el caso de que el modelo de propulsion del sistema sea

lineal y luego se mostrara que ocurre cuando el modelo de propulsion sea cuadratico.

3.4.1. Modelo con propulsion lineal

En la literatura es frecuente encontrar modelos de propulsion de helices en el que

las fuerzas de propulsion son proporcionales a la velocidad de la helice. Observando la

figura 2.4 se puede comprobar que esto no es mas que una aproximacion lineal en un

entorno de un punto de trabajo, por lo que la constante de proporcionalidad incluye

el valor medio de dicha velocidad angular.

En este apartado se considera fijo el angulo de orientacion (θ = cte) y nula la

velocidad del rotor de cola (ωp = cte = 0). Se controlara el movimiento de elevacion

mediante el rotor principal.

ϕ

ωg

Figura 3.1: Subsistema de Elevacion

63

Tal y como se expuso en el capıtulo 2, las ecuaciones del subsistema de elevacion

vienen dadas por:

Iϕϕ + GsS(ϕ) + GcC(ϕ) + Kϕ·ϕ = Lgωg (3.4.1)

Igωg = Ug − (Bg + Dg)ωg (3.4.2)

En este caso, el termino de propulsion y el de arrastre se han modelado como si fueran

lineales en velocidad (Lgωg y Dgωg) en vez de cuadraticos (Lg|ω|ω y Dg|ω|ω).

ϕ: Angulo de elevacion medido desde el plano horizontal.

Iϕ: Inercia del sistema de elevacion respecto al eje de giro.

ωg: Velocidad de la helice grande.

Ig: Inercia del motor-helice respecto a su eje de giro.

Lgωg: Par en el eje debido a la fuerza aerodinamica

de propulsion del rotor grande (Lift).

Kϕ·ϕ: Par de friccion.

GsS(ϕ) + GcC(ϕ): Par de gravedad. S().= sin() y C()

.= cos().

Ug: Par motor.

Bg: Constante de friccion del motor.

Dg: Constante de resistencia aerodinamica de la helice (Drag).

Reescribiendo las ecuaciones (3.4.1) y (3.4.2) en forma matricial

⎡⎢⎢⎣

Iϕ 0

0 Ig

⎤⎥⎥⎦ ·

⎡⎢⎢⎣

ϕ

ωg

⎤⎥⎥⎦ +

⎡⎢⎢⎣

GsS(ϕ) + GcC(ϕ) + Kϕ·ϕ − Lgωg

(Bg + Dg)ωg

⎤⎥⎥⎦ =

⎡⎢⎢⎣

0

Ug

⎤⎥⎥⎦ (3.4.3)

Se observa que hay una senal de actuacion (Ug) y dos grados de libertad (ϕ y ωg). Por

tanto, se trata de un sistema subactuado, en el sentido de que posee menos senales

de control que grados de libertad ([36]).

Linealizacion por realimentacion: entrada-estado

Se seguira el metodo general expuesto en la seccion 3.2.2, comenzando por:

64

1. Definicion del vector de estados:

x =

⎡⎢⎢⎣

ϕ − ϕeq

ϕ

ωg

⎤⎥⎥⎦ =

⎡⎢⎢⎣

x1

x2

x3

⎤⎥⎥⎦

2. Expresar la ecuacion (3.4.3) como:

x = f(x) + g(x)·u⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

x1

x2

x3

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦

=

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

x2

−GsS(ϕeq+x1)−GcC(ϕeq+x1)−Kϕ·x2+Lgx3

Iϕ

−(Bg+Dg)x3

Ig

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦

+

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

0

0

1Ig

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦·Ug

3. Comprobar que es posible la linealizacion por realimentacion.

ad0fg = g

adfg.= [f ·g]

.=

∂g

∂xf − ∂f

∂xg

donde:∂g

∂x= 0

y

∂f

∂x=

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

0 1 0

−Gs

IϕC(ϕeq + x1) + Gc

IϕS(ϕeq + x1) −Kϕ

Iϕ

Lg

Iϕ

0 0 −Bg+Dg

Ig

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦

Sustituyendo, se obtiene:

adfg =

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

0

− Lg

IgIϕ

Bg+Dg

I2g

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦

65

Finalmente,

ad2fg

.= [f, adfg]

.=

∂adfg

∂xf − ∂f

∂xadf (g)

donde:∂adfg

∂x= 0

resultando:

ad2fg =

⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣

Lg

IgIϕ

−KϕLg

IgI2ϕ

− Lg(Bg+Dg)

I2g Iϕ

(Bg+Dg)2

I3g

⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦

Es facil comprobar que los vectores {g, adf (g), ad2f (g)} son linealmente indepen-

dientes, donde el determinante de la matriz formada por los mismos resultaL2

g

I3g I2

ϕ�= 0,

siendo todos los parametros positivos. Ademas como los vectores son constantes, los

Corchetes de Lie de todas las combinaciones de los vectores {g, adf (g)} son nulas, por

lo que se pueden expresar como combinacion lineal de ellos mismos , y por tanto, el

conjunto {g, adf (g)} es involutivo en Ω.

Como se cumplen las dos condiciones, se puede afirmar que el sistema es linealizable

por realimentacion entrada-estado.

4. Calcular el nuevo vector de estado completo a partir del primer estado z1, mediante

la transformacion:

z(x) =[

z1 �Lfz1 . . . �Ln−1f z1

]T

(3.4.4)

Para ello se han de plantear las ecuaciones siguientes para encontrar el primer estado

z1. Se tendra que cumplir que:

∇z1·g = 0 (3.4.5)

∇z1·adfg = 0

∇z1·ad2fg �= 0

66

Sustituyendo en (3.4.5) se obtiene:

∇z1·g =∂z1

∂x1·g�1 +

∂z1

∂x2·g�2 +

∂z1

∂x3·g�3 =

∂z1

∂x1·0 +

∂z1

∂x2·0 +

∂z1

∂x3· 1Ig

=∂z1

∂x3· 1Ig

= 0

∇z1·adfg =∂z1

∂x1·adfg�1 +

∂z1

∂x2·adfg�2 +

∂z1

∂x3·adfg�3 =

=∂z1

∂x1·0 +

∂z1

∂x2·adfg�2 + 0·adfg�3 = 0

∇z1·ad2fg =

∂z1

∂x1·ad2

fg�1 +∂z1

∂x2·ad2

fg�2 +∂z1

∂x3·ad2

fg�3 =

=∂z1

∂x1·ad2

fg�1 + 0·ad2fg�2 + 0·ad2

fg�3 �= 0

donde �i representa la i-esima componente del vector.

Por lo que se demuestra que z1(x) = z1(x1). Eligiendo la funcion mas sencilla,

z1(x) = x1, se llega a que:

∇z1 =

[∂z1

∂x1

,∂z1

∂x2

,∂z1

∂x3

]=

[1 0 0

]por lo que �Lgz1 = ∇z1·g = 0 y �Lfz1(x) = ∇z1·f = x2.

Se calcula ∇(�Lfz1) obteniendo:

∇(�Lfz1) =[

0 1 0]

llegando a que �Lg �Lfz1 = ∇(�Lfz1)·g = 0. Del mismo modo, se resuelve:

�L2fz1(x) = ∇(�Lfz1)·f =

−GsS(ϕeq + x1) − GcC(ϕeq + x1) − Kϕ·x2 + Lgx3

Iϕ

A continuacion se calcula:

�Lg �L2fz1 = ∇(�L2

fz1)(x)·g =Lg

IϕIg

�= 0

tal y como se deseaba. Por ultimo se calculara �L3fz1 obteniendose:

�L3fz1 = ∇(�L2

fz1)·f =

(Kϕ (GsS(ϕeq + x1) + GcC(ϕeq + x1))

I2ϕ

)+

+

(GcS(ϕeq + x1) − GsC(ϕeq + x1)

Iϕ

+

(Kϕ

Iϕ

)2)·x2−

67

−(

Lg

Iϕ

(Kϕ

Iϕ

+Bg + Dg

Ig

))·x3 (3.4.6)

5. Finalmente, la senal de control a aplicar al actuador viene dada por la transfor-

macion:

u =ν − �L3

fz1

�Lg �L2fz1

Se puede observar que el difeomorfismo planteado esta bien definido para todo

valor del estado x. Ademas, la ley de control estara bien definida si y solo si �Lg �L2fz1

esta bien definida para todo valor del estado x, cosa que se cumple por ser una

constante distinta de cero. Por lo tanto, la linealizacion obtenida es global para todo

x.

6. El controlador externo tendra que ser disenado para un sistema lineal dado por

un triple integrador (tantos integradores como la dimension del vector x).

Linealizacion por realimentacion: entrada-salida

Una vez comprobado que es posible realizar una linealizacion entrada-estado, se

expondra como obtener la misma ley de control usando una linealizacion entrada-

salida.

El procedimiento consiste en derivar la salida respecto al tiempo repetidas veces

hasta que aparezca la entrada u, y despues disenar u de forma que la no linealidad

quede cancelada.

Se definira la salida de la forma mas sencilla. Se elegira h(x) = x1, que representa

el angulo de elevacion del sistema y es una variable medible. A continuacion se calcula

la primera derivada de y respecto al tiempo:

y = �Lfh + �Lghu

Sabiendo que �Lgh = ∇h·g, se tiene que:

∇h =∂h

∂x=

[∂h

∂x1

,∂h

∂x2

,∂h

∂x3

]=

[1 0 0

]

68

y por tanto:

∇h·g =[

1 0 0]·

⎡⎢⎢⎣

0

0

1Ig

⎤⎥⎥⎦ = 0

Por consiguiente, se ha de volver a derivar la salida, obteniendose:

y = �L2fh + �Lg �Lfhu

donde:

�Lfh = ∇h·f =[

1 0 0]·

⎡⎢⎢⎣

f�1

f�2

f�3

⎤⎥⎥⎦ = f�1 = x2

�Lg �Lfh = ∇(∇h·f)·g = ∇x2·g =[

0 1 0]⎡⎢⎢⎣

0

0

1Ig

⎤⎥⎥⎦ = 0

y por tanto se ha de volver a derivar.

y(3) = �L3fh + �Lg �L

2fhu

A continuacion se examina:

�Lg �L2fh = �Lg(�Lfx2)

�Lfx2 = ∇x2·f =[

0 1 0]·f = f�2

�Lg(f�2) = ∇(f�2)·g =[

∂f�2∂x1

∂f�2∂x2

∂f�2∂x3

]⎡⎢⎢⎣

0

0

1Ig

⎤⎥⎥⎦ =

∂f�2

∂x3

1

Ig

=Lg

IϕIg

�= 0

Debido a que �Lg �L2fh �= 0, el sistema tiene grado relativo 3. Ahora la senal de

control u se calculara tomando como nueva senal de control ν = y(3). De esta forma

se puede expresar la ley de control linealizante como:

ν = �L3fh + �Lg �L

2fhu

69

y despejando u,

u =ν − �L3

fh

�Lg �L2fh

con �Lg �L2fh =

Lg

IϕIg

�= 0 ∀x

Esta ley hara que el sistema se comporte, visto desde ν, como un triple integrador. A

continuacion se ha de calcular �L3fh. Este calculo es justamente el realizado en el caso

de la linealizacion entrada-estado (Ec. (3.4.6)), ya que para la salida elegida el grado

relativo del sistema coincide con el orden del sistema, el cual es 3. Por tanto no hay

dinamica cero, y la linealizacion entrada-salida para la salida elegida da lugar a una

linealizacion completa del sistema.

Controlador externo LQR

A continuacion se va a disenar el controlador del lazo externo que proporciona

la senal ν de entrada al sistema linealizado. Se han disenado dos controladores: un

controlador LQR y un controlador LQR con efecto integral.

El controlador LQR se ha disenado bajo la hipotesis de que el sistema resultante de

la linealizacion por realimentacion es un triple integrador. La ley de control dada por

el controlador LQR sera de la forma ν = kpr − ULQR, siendo r el angulo de cabeceo

de referencia y ULQR = Kc·z, donde Kc = [kp, kv, ka] sera obtenida resolviendo la

ecuacion de Riccati para horizonte infinito. Expresando el triple integrador en el

espacio de estados resulta:

z = A·z + B·ULQR

y = C·zdonde:

A =

⎡⎢⎢⎣

0 1 0

0 0 1

0 0 0

⎤⎥⎥⎦ B =

⎡⎢⎢⎣

0

0

1

⎤⎥⎥⎦ C =

[1 0 0

]

El controlador LQR se ha disenado en tiempo discreto para un tiempo de muestreo

de Tm = 0.01s, eligiendose como matriz de ponderacion del nuevo estado Q = CT C,

y como ponderacion de la senal de control r = 1. Haciendo uso de MatLab se ha

obtenido, para el sistema en tiempo discreto, Kc = [0.9900, 1.9851, 1.9900]. Notese,

70

que con la eleccion de Q = CT C se esta ponderando la primera componente del vector

de estado, que corresponde a la salida y.

Los resultados de simulacion, usando modelos de propulsion lineales tanto en la

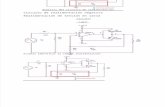
ley de control como en el simulador, se muestran en las figuras 3.2a, 3.2b y 3.2c,

donde respectivamente se muestran la senal de control ν procedente del controlador

LQR, la senal de control u aplicada al motor y el angulo de cabeceo ϕ del sistema.

Se hace notar que el valor permitido para la senal de control aplicada a los motores

es de |u| ≤ 1. Por encima de este valor el motor satura. Puede ocurrir que, debido a

0 10 20 30 40 50 60−0.3

−0.2

−0.1

0

0.1

0.2

0.3

0.4

0.5

0.6Linealizacion Entrada−Estado con LQR: Señal Externa de Control

Tiempo en segundos

V

0 10 20 30 40 50 60−0.1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9Linealizacion Entrada−Estado con LQR: Señal de Control al motor

Tiempo en segundos

ωU

0 10 20 30 40 50 60−35

−30

−25

−20

−15

−10

−5

0Linealizacion Entrada−Estado con LQR: Angulo de Elevacion

Ang

ulo

en g

rado

s

Tiempo en segundos

φ desφ

Figura 3.2: a) Senal de control procedente del LQR. b) Senal de control aplicada almotor. c) Angulo de cabeceo

las incertidumbres del modelo, sobre todo en los modelos de propulsion, no se consiga

realizar una linealizacion por realimentacion perfecta, por lo que para asegurar que

71

el sistema resultante sea al menos de tipo 1, se ha anadido un cuarto integrador. De

esta forma, se conseguira obtener un error de posicion nulo en regimen permanente.

El sistema ampliado con el integrador adicional vendra dado por:

za = Aa·za + Ba·ULQR

y = Ca·za

Aa =

[A 0

−C 0

]Ba =

[B

0

]Ca =

[C 0

0 1

]

El controlador ha sido calculado en tiempo discreto para un Tm = 0.01s, obte-

niendose:

Kc = [2.8717, 3.6869, 2.7102,−0.9864]

Los resultados de las leyes de control se muestran en las figuras 3.3a, 3.3b y 3.3c.

Igual que en el caso anterior, estas representan respectivamente la senal de control

externo ν, la senal de control linealizante u, y el angulo de cabeceo ϕ. En la figura

3.3b puede observarse como la senal de control u no llega a saturar (|u| ≤ 1 ∀t).