APPUNTI DI GASDINAMICA

CAPITOLO 1

DERIVAZIONE DELLE EQUAZIONI DI

BILANCIO

M. GermanoDip. di Ing. Aeronautica e Spaziale

Politecnico di Torino

1

Indice

1 Cenni di meccanica statistica 31.1 Funzione di distribuzione molecolare . . . . . . . . . . . . . . 31.2 Equilibrio termodinamico . . . . . . . . . . . . . . . . . . . . 4

2 Bilancio di massa e di quantita di moto 62.1 Equazioni di Eulero . . . . . . . . . . . . . . . . . . . . . . . 82.2 Equazioni di Navier-Stokes . . . . . . . . . . . . . . . . . . . 92.3 Interpretazione cinetica degli sforzi viscosi . . . . . . . . . . . 132.4 Viscosita di un gas e di una miscela . . . . . . . . . . . . . . 15

3 Bilancio dell’energia 163.1 Interpretazione cinetica dei flussi di calore . . . . . . . . . . . 18

4 APPENDICE al capitolo 1 214.1 Atto di moto elementare . . . . . . . . . . . . . . . . . . . . . 214.2 Streamlines, pathlines, streaklines. . . . . . . . . . . . . . . . 224.3 Riepilogo equazioni di bilancio. . . . . . . . . . . . . . . . . . 23

2

1 Cenni di meccanica statistica

Il significato fisico delle grandezze termodinamiche e di campo utilizzatenella descrizione fenomenologica di un flusso va ricercato nella descrizionee nella interpretazione statistica del comportamento di un gas1. Le pro-prieta fenomenologiche, di larga scala, dei gas sono direttamente legate allastruttura delle molecole che li compongono e alle loro interazioni. Notiamoche alla pressione di 1.013bar e alla temperatura di 273.15K una Mole digas occupa 22.4m3 e contiene 6.02 · 1026 molecole, (numero di Avogadro), ilche avvisa che una descrizione dettagliata del moto delle singole molecole epraticamente impossibile ed impone una descrizione statistica.

1.1 Funzione di distribuzione molecolare

La descrizione statistica e basata su funzioni di distribuzione molecolare.Definiamo come

dN = f (x, y, z, u, v, w, t) dudvdw (1)

il numero dN di molecole per unita di volume aventi velocita compresanell’intervallo u ÷ u + du, v ÷ v + dv, w ÷ w + dw, dove si intende cheil riferimento geometrico utilizzato e quello Cartesiano. Dalla definizionediscende che la densita di molecole N (x, y, z, t), numero di molecole perunita di volume, e data dall’integrale su tutte le possibili velocita

N (x, y, z, t) =

∫dN =

∫ ∞−∞

du

∫ ∞−∞

dv

∫ ∞−∞

f (x, y, z, u, v, w, t) dw (2)

mentre la densita di massa % e data da

% (x, y, z, t) = mN (x, y, z, t) (3)

essendo m la massa molecolare delle singole molecole.Attraverso sempre la funzione di distribuzione f(x, y, z, u, v, w, t) possia-

mo inoltre calcolare le componenti u, v, w della velocita media o d’insiemedelle molecole, quelle effettivamente misurate a livello macroscopico, datedagli integrali

u (x, y, z, t) =1

N

∫udN =

1

N

∫ufdudvdw

v (x, y, z, t) =1

N

∫vdN =

1

N

∫vfdudvdw

w (x, y, z, t) =1

N

∫wdN =

1

N

∫wfdudvdw

1Gas:voce foggiata (1600) dal chimico J. B. Van Helmont col significato di vapore sottiledal latino chaos, greco χαos, massa informe, che gia Paracelso aveva usato in senso simile.(dal Dizionario Enciclopedico Treccani)

3

dove si e introdotta la simbologia compatta∫dudvdw =

∫ ∞−∞

du

∫ ∞−∞

dv

∫ ∞−∞

dw

Adottando il punto di vista statistico possiamo quindi pensare che la velocitadi ogni molecola, espressa in componenti cartesiane dai valori u, v, w, sia lasomma di due contributi, uno statistico, di campo, che corrisponde puntoper punto alla velocita media globale di un gran numero di molecole e cheabbiamo indicato come u, v, w ed uno fluttuante, a valor medio nullo, eche corrisponde alla cosiddetta agitazione termica, dato dalle componentiu′, v′, w′

u = u+ u′

v = v + v′

w = w + w′

(4)

E’ chiaro per quanto detto che

u′ = 0 v′ = 0 w′ = 0 (5)

mentre l’energia complessiva traslazionale media per molecola puo esserescomposta nelle due parti

m (uu+ vv + ww)

2=m (uu+ vv + ww)

2+m(u′u′ + v′v′ + w′w′

)2

(6)

La prima rappresenta chiaramente la parte baricentrale di larga scala, men-tre la seconda

εt =m(u′u′ + v′v′ + w′w′

)2

(7)

definisce l’energia interna traslazionale media per molecola εt. Si puo infinedefinire una velocita equivalente di agitazione termica vat data da

vat =

(2εtm

) 12

(8)

1.2 Equilibrio termodinamico

In condizioni di equilibrio termodinamico assoluto2 la funzione di distribu-zione molecolare feq(u, v, w) acquista un valore ben preciso, universale, chedipende unicamente dalla temperatura assoluta T del gas in esame. La suaforma esplicita e data dalla meccanica statistica e corrisponde al prodotto

2Uguale pressione p, temperatura T , composizione chimica e velocita media u, v, wdappertutto. La funzione di distribuzione molecolare d’equilibrio feq diventa quindiindipendente sia dallo spazio che dal tempo.

4

di tre gaussiane, una per ogni componente della velocita, centrate intornoai rispettivi valori medi u, v, w. Si ha

u′u′ = v′v′ = w′w′ =kBT

mu′v′ = v′w′ = w′u′ = 0 (9)

dove kB e la costante di Boltzmann

kB = 1.38 · 10−23joule/Kelvin/molecola (10)

e l’energia media traslazionale per molecola e data da

m (uu+ vv + ww)

2=m (uu+ vv + ww)

2+

3kBT

2(11)

Si ha quindi che l’energia interna traslazionale media per molecola, εt, edata da

εt =3

2kBT (12)

mentre quella per mole e data da

Et = NAεt =3

2RT (13)

dove R e la costante universale dei gas

R = 8.314 · 103joule/Kelvin/Mole (14)

e Et l’energia interna traslazionale molare, cioe quella posseduta da unnumero di molecole pari al numero di Avogadro NA

NA = 6.02 · 1026molecole/Mole (15)

Si deduce di conseguenza che

kB =R

NA(16)

e in base alla (12) ricaviamo la velocita di agitazione termica vat

vat =

(2εtm

) 12

=

(3kBT

m

) 12

=

(3RT

M

) 12

(17)

dove M e la massa molare del gas M = mNA. E’ interessante confrontarevat con la velocita di propagazione del suono c

c =

(γRT

M

) 12

(18)

dove γ e il rapporto dei calori specifici.

5

Figura 1:

2 Bilancio di massa e di quantita di moto

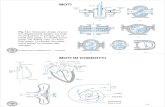
Notiamo subito che la struttura di una equazione di bilancio e del tuttogenerale e puo essere ricondotta, vedi figura (1), ad un semplice pareggiotra variazioni temporali, flussi e produzioni delle varie grandezze.

Se infatti indichiamo con G una generica grandezza per unita di volu-me, la massa delle molecole per unita di volume, la quantita di moto dellemolecole per unita di volume, l’energia delle molecole per unita di volume,allora la quantita relativa contenuta nel cubetto di controllo dxdydz e datada Gdxdydz, e la sua variazione nel tempo e data da

∂ (Gdxdydz)

∂t= Φxdydz −

(Φx +

∂Φx

∂xdx

)dydz

+ Φydxdz −(

Φy +∂Φy

∂ydy

)dxdz

+ Φzdydz −(

Φz +∂Φz

∂zdz

)dxdy + Pdxdydz (19)

dove Φx,Φy,Φz indica il flusso della stessa attraverso le superfici di contornoe P la eventuale produzione per unita di tempo e di volume. Si ottiene

∂G

∂t+∂Φx

∂x+∂Φy

∂y+∂Φz

∂z= P (20)

Consideriamo ora il bilancio 1 della massa delle molecole, e notiamo che

1Ricordiamo il significato della simbologia compatta∫dN =

∫fdudvdw =

∫ ∞−∞

fdu

∫ ∞−∞

dv

∫ ∞−∞

dw

6

nei termini della funzione f la massa di molecole per unita di volume G e iflussi Φx,Φy,Φz relativi alle varie direzioni x, y, z sono dati da

G = m

∫dN = mN = %

Φx = m

∫udN = %

1

N

∫udN = %u

Φy = m

∫vdN = %v

Φz = m

∫wdN = %w (21)

mentre la produzione P e ovviamente nulla, per cui si ottiene

∂%

∂t+∂%u

∂x+∂%v

∂y+∂%w

∂z= 0 (22)

Se ora indichiamo con Gx la quantita di moto per unita di volume dellemolecole lungo la direzione x, con Φxx,Φxy,Φxz i relativi flussi attraverso lesuperfici di contorno, con Px la produzione di quantita di moto per unita divolume e di tempo, abbiamo, in assenza di forze esterne

Gx = m

∫udN = %u

Φxx = m

∫uudN = %

1

N

∫uudN = %uu = %uu+ %u′u′

Φxy = m

∫uvdN = %uv = %uv + %u′v′

Φxz = m

∫uwdN = %uw = %uw + %u′w′

Px = 0 (23)

per cui si ottiene

∂%u

∂t+∂%uu

∂x+∂%uv

∂y+∂%uw

∂z= −∂%u

′u′

∂x− ∂%u′v′

∂y− ∂%u′w′

∂z(24)

Analogamente avremo per i bilanci di quantita di moto lungo le direzioni ye z per cui si ottiene

∂%v

∂t+∂%vu

∂x+∂%vv

∂y+∂%vw

∂z= −∂%v

′u′

∂x− ∂%v′v′

∂y− ∂%v′w′

∂z(25)

∂%w

∂t+∂%wu

∂x+∂%wv

∂y+∂%ww

∂z= −∂%w

′u′

∂x− ∂%w′v′

∂y− ∂%w′w′

∂z(26)

7

Notiamo che nelle equazioni di bilancio della quantita di moto del motomedio i termini fx, fy, fz

fx = −∂%u′u′

∂x− ∂%u′v′

∂y− ∂%u′w′

∂z

fy = −∂%v′u′

∂x− ∂%v′v′

∂y− ∂%v′w′

∂z

fz = −∂%w′u′

∂x− ∂%w′v′

∂y− ∂%w′w′

∂z(27)

appaiono come forze esterne per unita di volume, avendosi

∂%u

∂t+∂%uu

∂x+∂%uv

∂y+∂%uw

∂z= fx

∂%v

∂t+∂%vu

∂x+∂%vv

∂y+∂%vw

∂z= fy

∂%w

∂t+∂%wu

∂x+∂%wv

∂y+∂%ww

∂z= fz

(28)

2.1 Equazioni di Eulero

Nelle equazioni sopra scritte compaiono oltre alle grandezze %, u, v, w, anchele sei grandezze

%u′u′ %v′v′ %w′w′ %u′v′ %u′w′ %v′w′

che hanno le dimensioni di sforzi, forze per unita di superficie, e che vannocalcolate. Nel caso di equilibrio termodinamico assoluto, (equilibrio chimico,meccanico, termico, e quindi assenza di qualsiasi anisotropia o disomogeneitanelle grandezze che descrivono lo stato del gas compreso il campo di velocitadel moto medio u, v, w), abbiamo visto che

u′v′ = 0 u′w′ = 0 v′w′ = 0 (29)

u′u′ = v′v′ = w′w′ =kBT

m=RT

M(30)

Dalla legge dei gas perfetti si ha

NkBT = %R

MT = p (31)

con p pressione del gas, e quindi si ottiene

%u′v′ = 0 %u′w′ = 0 %v′w′ = 0 (32)

%u′u′ = %v′v′ = %w′w′ = p (33)

8

Le equazioni di bilancio ottenute sotto questa ipotesi sono le cosiddetteequazioni di Eulero e sono esplicitamente date dalle espressioni

∂%u

∂t+∂%uu

∂x+∂%uv

∂y+∂%uw

∂z= −∂p

∂x

∂%v

∂t+∂%vu

∂x+∂%vv

∂y+∂%vw

∂z= −∂p

∂y

∂%w

∂t+∂%wu

∂x+∂%wv

∂y+∂%ww

∂z= −∂p

∂z

(34)

In esse si fa sentire l’effetto dell’agitazione termica unicamente sotto formadi forze di pressione. Lo sforzo esercitato su di una parete e normale adessa e non dipende dall’orientamento della superficie nello spazio, (legge diPascal).

2.2 Equazioni di Navier-Stokes

In realta l’agitazione termica non soltanto contribuisce alla energia internadel gas con la parte traslazionale Et

Et =M(u′u′ + v′v′ + w′w′

)2

(35)

e alla dinamica del moto medio con le forze di pressione p

p = %u′u′ = %v′v′ = %w′w′ =2

3N εt (36)

ma contribuisce anche al trasporto caotico da punto a punto di massa, quan-tita di moto ed energia del moto medio, dando luogo come vedremo aglieffetti diffusivi, viscosi e conduttori di calore. Questi effetti si manifestanoin presenza di gradienti di velocita del moto medio, di temperatura e di con-centrazione.In questi casi l’equilibrio termodinamico per la funzione f none piu assicurato ed essa non ha piu una forma universale ma va calcolatacaso per caso seguendo l’evoluzione delle molecole nello spazio-tempo e l’ef-fetto degli urti su di esse. Essendo f = f (x, y, z, u, v, w, t), la sua variazionetotale nel tempo e data da

∂f

∂t+ u

∂f

∂x+ v

∂f

∂y+ w

∂f

∂z+ ax

∂f

∂u+ ay

∂f

∂v+ az

∂f

∂w= J (37)

dove le componenti cartesiane dell’accelerazione ax, ay, az sono legate allaforza esercitata dall’esterno sulle molecole, Fx, Fy, Fz

ax =Fx

may =

Fy

maz =

Fz

m(38)

e dove il termine J e il cosiddetto termine collisionale, che descrive l’effettodegli urti sulla f . L’equazione (37) e detta equazione di Boltzmann e le sue

9

proprieta e la forma esplicita del termine J possono essere esaminate suilibri di teoria cinetica dei gas ad essa dedicati, vedi per esempio [1].La suarisoluzione e in generale molto complessa e in questa sede ci limiteremo adalcune considerazioni di scala utili ad interpretare soluzioni perturbative chevanno sotto il nome di soluzioni di Chapman e Enskog.Notiamo innanzitutto che una grandezza fondamentale per quel che riguardala evoluzione spazio-temporale di f e il libero cammino medio molecolare l,definito come la distanza mediamente percorsa tra due urti successivi da unamolecola. Al fine di determinare questa lunghezza calcoliamo innanzituttoil numero medio di collisioni che una molecola subisce nell’unita di tempo.Seindichiamo questa grandezza con ϑ, essa sara data dal numero di molecolespazzate mediamente da una molecola lungo il suo cammino per unita ditempo.Se notiamo che il volume spazzato durante l’unita di tempo e datoda vatσ, dove σ e la sezione d’urto della molecola, il suo ingombro frontale,allora si ha evidentemente

ϑ = N vatσ (39)

essendoN il numero di molecole per unita di volume. Notiamo che la sezioned’urto molecolare relativa ad incontri a due a due e data dall’espressione

σ = πd2 (40)

dove d e il diametro ottico, non il raggio, delle molecole che si urtano.Intabella sono riportati alcuni valori relativi alle molecole che compongonol’aria

Molecola O2 N2 O N NODiametro ottico in Angstrom 3.4 3.7 3.1 3.0 3.5

Notiamo ora che il tempo collisionale medio τ e dato dalla espressione

τ =1

ϑ(41)

e dato che la molecola durante questo tempo viaggia mediamente con lavelocita di agitazione termica vat, otteniamo

l = vatτ =1

Nσ(42)

Il libero cammino medio e di importanza fondamentale in quanto il suo rap-porto con una lunghezza caratteristica L del corpo investito dalla corrente,rapporto detto numero di Knudsen, Kn

Kn =l

L(43)

ci dice se la cinetica del mezzo e dominata dalle collisioni tra le molecoleo dalle collisioni con il corpo.In quest’ultimo caso, Kn > 1, il mezzo non

10

puo piu essere considerato come un mezzo continuo, e va trattato come gasrarefatto.Notiamo che il libero cammino medio scala inversamente con ladensita

l = vatτ =m

%σ(44)

e che il suo valore in aria standard e di 660 Angstrom, il che comporta chealla quota di 80 km, dove la densita si e ridotta nel rapporto di 10−5, illibero cammino medio e di circa 1 cm. Il numero di Knudsen relativo peresempio alle dimensioni tipiche di un satellite puo quindi diventare ad altaquota dell’ordine dell’unita, e in tal caso siamo in condizioni di gas rare-fatto. Cade quindi non solo l’ipotesi di equilibrio termodinamico ma anchela stessa ipotesi del continuo che giustifica l’adozione di una funzione f eoccorre studiare il problema con le metodologie proprie del moto delle mo-lecole libere. Se invece, all’estremo opposto, siamo in presenza di numeri diKnudsen molto piccoli, allora non solo e giustificato l’approccio del continuoutilizzato finora ma anche l’ipotesi di equilibrio termodinamico e corrobo-rata. Sulla base di tali considerazioni Chapman e Enskog hanno sviluppatodelle soluzioni perturbative della (37) con espansioni nel numero di Knud-sen e in presenza di moto medio con gradienti di velocita. Naturalmente ilprimo termine della serie, f0, ottenuto nel limite Kn = 0, e quello relati-vo all’equilibrio,f0 = feq, mentre il primo termine introduce una correzioneperturbativa f1, che da il seguente risultato

%u′v′ = −τxy = −µ(∂u

∂y+∂v

∂x

)(45)

%u′w′ = −τxz = −µ(∂u

∂z+∂w

∂x

)(46)

%v′w′ = −τyz = −µ(∂v

∂z+∂w

∂y

)(47)

%u′u′ = p− τxx = p− 2µ∂u

∂x+

2

3µ∆ (48)

%v′v′ = p− τyy = p− 2µ∂v

∂y+

2

3µ∆ (49)

%w′w′ = p− τzz = p− 2µ∂w

∂z+

2

3µ∆ (50)

dove ∆, divergenza del campo di velocita, e data da

∆ =∂u

∂x+∂v

∂y+∂w

∂z(51)

e dove µ e il coefficiente di viscosita del gas. Una osservazione va fattaper quel che riguarda la scelta dei segni che convenzionalmente sono presi

11

in modo da rendere gli sforzi τij interpretabili come sforzi fatti dal mondoesterno sul volumetto di controllo.

Le equazioni di bilancio cosı ottenute sono le cosiddette equazioni diNavier-Stokes ed una ulteriore giustificazione della relazione costitutiva trasforzi e gradienti di velocita puo essere data su basi cinematiche considerandol’atto di moto elementare in un mezzo fluido, vedi Appendice. Come e notoesso puo essere scomposto in una roto-traslazione rigida piu tre dilatazioniortogonali tra loro a volume costante piu una dilatazione isotropa volumica.Notiamo che i termini

sxx =∂u

∂x− 1

3∆ sxy = 1

2

(∂u

∂y+∂v

∂x

)sxz = 1

2

(∂u

∂z+∂w

∂x

)

syx = 12

(∂v

∂x+∂u

∂y

)syy =

∂v

∂y− 1

3∆ syz = 1

2

(∂v

∂z+∂w

∂y

)

szx = 12

(∂w

∂x+∂u

∂z

)szy = 1

2

(∂w

∂y+∂v

∂z

)szz =

∂w

∂z− 1

3∆

corrispondono alla parte dilatatoria senza variazione di volume del tensoredei gradienti di velocita.Abbiamo cioe

τxy = τyx = 2µsxy τxz = τzx = 2µsxz τyz = τzy = 2µsyz

τxx = 2µsxx τyy = 2µsyy τzz = 2µszz

Gli sforzi non dipendono quindi dalla parte roto-traslatoria dello stesso nedalla dilatazione isotropa volumica in quanto la cosiddetta viscosita di vo-lume, (bulk viscosity), che in questo caso manifesterebbe la sua esistenzae generalmente trascurabile. Notiamo infine che l’energia interna traslazio-nale per unita di volume conserva lo stesso valore sia in equilibrio che indisequilibrio

%u′u′ + %v′v′ + %w′w′

2=

3

2p (52)

essendo

τxx + τyy + τzz = 0 (53)

e cio e diretta conseguenza dell’aver posto la bulk viscosity uguale a zero. Lapresenza di una viscosita di volume ζ comporterebbe infatti che

τxy = τyx = 2µsxy τxz = τzx = 2µsxz τyz = τzy = 2µsyz

τxx = 2µsxx − ζ∆ τyy = 2µsyy − ζ∆ τzz = 2µszz − ζ∆

il che ha delle conseguenze a livello della termodinamica del mezzo, in quantosi avrebbe

%u′u′ + %v′v′ + %w′w′

2=

3

2(p+ ζ∆) (54)

12

Notiamo infine che le τij , i 6= j si manifestano in flussi di taglio, contraria-mente alle τij , i = j che si manifestano tipicamente nei flussi di punta, esono quindi generalmente oscurate dalle forze di pressione.

2.3 Interpretazione cinetica degli sforzi viscosi

Vediamo ora di interpretare fisicamente, sempre a livello di teoria cineticadei gas, le espressioni precedenti che danno i valori delle correlazioni

%u′u′ %u′v′ %u′w′ %v′v′ %v′w′ %w′w′ (55)

Notiamo che in esse compaiono ora non solo i termini di pressione ma anchedei nuovi termini che dipendono dal gradiente di velocita. Esse inoltre di-pendono in disequilibrio termodinamico da un nuovo termine, il coefficientedi viscosita µ che va interpretato dal punto di vista fisico e calcolato in ter-mini numerici. Ricordiamo che i termini (55) hanno il significato di sforziesercitati sulle pareti del volumetto di controllo, sono cioe dimensionalmen-te delle forze per unita di superficie. Consideriamo per esempio il termine%u′v′ . Esso fisicamente rappresenta il flusso di quantita di moto trasportatodalla agitazione termica e diretto nella direzione x attraverso la superficienormale alla direzione y.Un flusso di quantita di moto e una variazione diquantita di moto per unita di tempo e di superficie, quindi una forza perunita di superficie, quindi uno sforzo:nel caso di %u′v′ lo sforzo esercitatonella direzione x su di una superficie normale alla direzione y. In assenza digradienti di velocita del moto medio questi sforzi cinetici sono tutti normalialle superfici considerate e pari alla pressione p;nel caso di disomogeneitaspaziali del moto medio si ha un disequilibrio della funzione f e la conse-guente nascita di sforzi viscosi. Al fine di interpretare fisicamente tali sforzie opportuno considerare un caso semplice di campo di moto medio disomo-geneo, quello di puro moto di taglio in cui si ha una sola componente nonnulla del moto medio, per esempio la u, che dipende spazialmente dalla solay, u (y), vedi figura (2).

In tal caso abbiamo

%u′v′ = −τxy = −µ∂u∂y

%u′w′ = 0 %v′w′ = 0 (56)

%u′u′ = %v′v′ = %w′w′ = p (57)

Notiamo che l’unita di misura del coefficiente di viscosita µ e nel sistema SIkg/m/sec.Si ricava che la grandezza

ν =µ

%(58)

detta viscosita cinematica, ha le dimensioni di una velocita per una lunghez-za, e la sua unita di misura e, sempre nel sistema SI, data in m2/sec.Dal

13

Figura 2:

punto di vista dimensionale ν non puo dipendere altro che dalla velocitadi agitazione termica vat e dal libero cammino medio molecolare l, unichegrandezze fisiche di scala che siano state introdotte finora. Si ha quindi perpure considerazioni di analisi dimensionale che

ν ' vatl µ ' %vatl (59)

Questa relazione puo essere anche spiegata in termini piu fisici nel seguentemodo.Sempre da figura (2) notiamo che il flusso %u′v′ dovuto al trasportocaotico di quantita di moto attraverso la superficie normale alla direzione ydi quantita di moto diretta lungo la direzione x e dato fisicamente da

%u′v′ ' −m (u+ du)N vat +muN vat (60)

Se ora scriviamo

du =du

dydy (61)

e considerando che la scala di dy e data dal libero cammino medio molecolarel, cioe che fisicamente il trasporto caotico di quantita di moto avviene su diuna distanza dell’ordine di l, si ottiene

%u′v′ ' −mN vatldu

dy(62)

Nel caso di puro flusso di taglio considerato si ha quindi

τxy = µdu

dy(63)

e per confronto otteniamo

ν ' vatl µ ' %vatl (64)

essendo % = Nm. Notiamo che dalla figura (2) si ha anche un ulteriorechiarimento sulla regola dei segni di cui si e parlato in precedenza; il flusso%u′v′ e in questo caso negativo, ma la τxy e positiva in quanto il volumettodi controllo e tirato dagli strati superiori esterni del fluido nella direzionedelle x positive.

14

2.4 Viscosita di un gas e di una miscela

Abbiamo visto che il coefficiente di viscosita µ dipende dal libero camminomedio l.Dalla teoria cinetica dei gas si ha

l ' 1

Nσ(65)

dove σ e la sezione d’urto collisionale tra le molecole in esame.Notiamo che iltempo medio collisionale τ , cioe il tempo che intercorre tra un urto e l’altro,e dato da

τ ' l

vat(66)

Sostituendo nella (64) si ottiene

µ ' mvatσ

(67)

con m massa molecolare.Si vede da questa espressione che nel caso di un gasideale composto da molecole a palle di biliardo, tali cioe che l’interazionereciproca sia nulla ad un distanza tra i centri maggiore del diametro, einfinita se minore, allora la viscosita e data da

µ ' (3kB)12m

12T

12

σ0(68)

dove a vat e sostituita la sua espressione esplicita nei termini della temperatu-ra assoluta e σ0 e la sezione d’urto geometrica. Notiamo che µ dipende dallaradice quadrata della temperatura assoluta T , e tanto piu piccola quantopiu piccola e la massa molecolare m e tanto piu grande quanto piu piccolae la sezione d’urto σ0.In realta il campo di forze che si stabilisce tra duemolecole durante un urto non e del tutto assimilabile a quello che si ha tradue palle da biliardo, il che porta ad avere come distanza media d’intera-zione durante un urto non il diametro delle molecole ma una distanza cheaumenta al diminuire della energia di collisione.Cio porta ad una variazionedella sezione d’urto σ con T , data da

σ = σ0

(1 +

χ

T

)(69)

e detta approssimazione di Sutherland.Naturalmente χ ha le dimensioni diuna temperatura, e per T →∞ si ha σ → σ0.Se sostituiamo questa espres-sione per la sezione d’urto σ nella espressione della viscosita µ data dalla(67) otteniamo la cosiddetta espressione di Sutherland

µ = ST

32

T + χ(70)

15

Nella tabella che segue sono dati i valori delle costanti χ ed S per vari gas,con µ misurata nel sistema SI, e cioe in kg/m/sec.

S · 106 χO2 1.65 110N2 1.39 102H2 0.65 71He 1.52 98CO2 1.56 233CO 1.40 109NH3 1.54 472Aria 1.46 110

Notiamo che in tabella compare anche una miscela di gas, l’aria, per la qualei valori di S e χ dati hanno piu un valore di correlazione empirica che altro.Ilproblema di determinare la viscosita di una miscela date le viscosita dei suoicomponenti e tutt’altro che semplice [2], ed una formulazione semi- empiricae quella data dal Wilke [3] che porta al seguente risultato

µ =∑i

µi

1 +∑k 6=i

Gikxkxi

−1 (71)

dove

Gik =

(1 +

(µiµk

) 12(mk

mi

) 14

)2

232

(1 +

mi

mk

) 12

(72)

e dove µi, xi e mi sono rispettivamente le viscosita, le frazioni molari ele masse molecolari dei singoli componenti.Terminiamo questa parte segna-lando infine delle espressioni approssimate che presentano una certa uti-lita nei calcoli essendo monomiali come forma.Per l’aria e nell’intorno dellatemperatura ambiente si ha con buona approssimazione

µ = µ288

(T

288

)ω

(73)

con ω = 0.75 e µ288 = 1.78 · 10−5kg/m/sec viscosita dell’aria standard.

3 Bilancio dell’energia

Abbiamo finora eseguito il bilancio della massa e quello della quantita dimoto ed abbiamo ottenuto le equazioni di Eulero nel caso di una funzionef d’equilibrio, le equazioni di Navier-Stokes nel caso di una funzione f de-formata dai gradienti di velocita del moto medio.Vediamo ora di eseguire

16

il bilancio della energia.In questo caso abbiamo come energia per unita divolume

G = m

∫(ei +

uu+ vv + ww

2)dN

= %

(ei +

uu+ vv + ww

2

)(74)

e come flussi

Φx = m

∫(ei +

uu+ vv + ww

2)udN

= %

(eiu+

uuu+ uvv + uww

2

)(75)

Φy = m

∫(ei +

uu+ vv + ww

2)vdN

= %

(eiv +

vuu+ vvv + vww

2

)(76)

Φz = m

∫(ei +

uu+ vv + ww

2)wdN

= %

(eiw +

wuu+ wvv + www

2

)(77)

con ei = ei + e′i energia interna roto-vibro-elettronica e di legame per unita

di massa, e dove ora il vettore Φx,Φy,Φz rappresenta il flusso d’energiaattraverso le superfici di contorno. Anche in questo caso P , produzione dienergia, e ovviamente nulla e inoltre possiamo scrivere

uu = uu+ u′u′ vv = vv + v′v′ ww = ww + w′w′ (78)

eiu = eiu+ e′iu′ eiv = eiv + e

′iv′ eiw = eiw + e

′iw′ (79)

uuu+ uvv + uww

2= u

(u2 + v2 + w2

2

)+

u

(u′u′ + v′v′ + w′w′

2

)+ uu′u′ + vu′v′ +

wu′w′ + u′(u′u′ + v′v′ + w′w′

2

)vuu+ vvv + vww

2= ..........

wuu+ wvv + www

2= .......... (80)

17

per cui ponendo

qx = %u′(e′i +

u′u′ + v′v′ + w′w′

2

)qy = .......

qz = ....... (81)

si ha formalmente

∂ (%E)

∂t+∂ ((%E + p) u)

∂x+∂ ((%E + p) v)

∂y+∂ ((%E + p) w)

∂z=

∂ (τxxu+ τxyv + τxzw − qx)

∂x+

∂ (τyxu+ τyyv + τyzw − qy)

∂y+

∂ (τzxu+ τzyv + τzzw − qz)∂z

(82)

dove

E = ei +u′u′ + v′v′ + w′w′

2+u2 + v2 + w2

2

= e+u2 + v2 + w2

2(83)

Notiamo che nei termini dell’entalpia d’arresto o totale H

H = h+u2 + v2 + w2

2= e+

p

%+u2 + v2 + w2

2(84)

si ha

∂ (%E)

∂t+∂ (%Hu)

∂x+∂ (%Hv)

∂y+∂ (%Hw)

∂z=

∂ (τxxu+ τxyv + τxzw − qx)

∂x+

∂ (τyxu+ τyyv + τyzw − qy)

∂y+

∂ (τzxu+ τzyv + τzzw − qz)∂z

(85)

3.1 Interpretazione cinetica dei flussi di calore

Il termine vettoriale

qx = %u′(e′i +

u′u′ + v′v′ + w′w′

2

)= %u′e′ (86)

che compare nella equazione di bilancio dell’energia corrisponde al trasportocaotico di energia caotica dovuto al moto di agitazione termica.Anche in

18

questo caso la teoria cinetica dei gas ha sviluppato teorie che permettonodi calcolare la funzione f nel caso in cui siano presenti nel flusso non sologradienti di velocita ma anche gradienti di temperatura T . Sulla loro baseabbiamo

qx = −λ∂T∂x

qy = −λ∂T∂y

qz = −λ∂T∂z

(87)

dove λ e il coefficiente di conducibilita termica. La giustificazione di questaespressione che lega in maniera elementare flussi di calore a gradienti ditemperatura puo essere data in maniera molto semplice sulla base deglistessi ragionamenti fisici utilizzati per determinare il coefficiente di viscosita.Dalla figura (2) notiamo che il flusso qy dovuto al trasporto caotico di energiainterna attraverso la superficie normale alla direzione y e dato fisicamenteda

qy ' −m (e+ de)N vat +meN vat (88)

dove e =∫cvT e l’energia interna media per unita di massa e dove cv e il

calore specifico per unita di massa a volume costante. Se ora scriviamo

de =de

dydy (89)

e considerando che come nel caso del trasporto di quantita di moto la scaladi dy e data dal libero cammino medio molecolare l, cioe che fisicamenteanche il trasporto caotico di energia avviene su di una distanza dell’ordinedi l, si ottiene

qy ' −mN vatlde

dy(90)

cioe

qy ' −mcvN vatldT

dy(91)

e, per confronto con la (87),

λ ' vatlNmcv ' µcv (92)

Notiamo che la scelta del segno nella determinazione del flusso qx, qy, qz etale da rendere le espressioni trovate coerenti con le leggi fenomenologiche,(Legge di Fourier), in cui λ e una costante essenzialmente positiva e i flussidi calore sono positivi se vanno da luoghi a temperatura piu alta verso luoghia temperatura piu bassa.Notiamo anche da quanto detto che il numero diPrandtl definito come

Pr =µcpλ

(93)

19

con cp = γcv calore specifico per unita di massa a pressione costante, e peri gas dell’ordine dell’unita. Sempre dalla teoria cinetica dei gas e nel casodi un gas dotato di di sola energia interna traslazionale, (gas monoatomicocon variazioni di energia interna elettronica trascurabili nell’intervallo ditemperature considerato), si ha piu precisamente

λ =5

2µcv Pr =

2

3(94)

essendo in tal caso γ = 53 . Nel caso in cui il gas e dotato di energia in-

terna non solo traslazionale ma anche roto-vibro-elettronica allora convienescindere cv nelle due parti

cv =1

γ − 1

R

M= cvt + cvi (95)

con

cvt =3

2

R

Mcvi =

5− 3γ

2 (γ − 1)

R

M(96)

e si puo scrivere

λ =5

2µcvt + αµcvi (97)

dove α e il fattore correttivo di Eucken.Il fatto che α non sia uguale a 52

significa che l’energia interna traslazionale e quella roto-vibro-elettronicanon sono trasferite esattamente allo stesso modo dalla agitazione termica.Eucken propose per α il valore 1.In tal caso il numero di Prandtl e datodalla espressione

Pr =4γ

9γ − 5(98)

Una buona approssimazione per il numero di Prandtl dell’aria, valida sudi un intervallo abbastanza ampio di temperature e Pr = 0.71. Ulterioridettagli sul calcolo di λ per l’aria ad alta temperatura e nel caso di miscelesi puo trovare sul Dorrance [4]. Notiamo infine che una grandezza ricavatadalla conducibilita termica e analoga alla viscosita cinematica e la diffusivitatermica κ

κ =λ

%cp(99)

avente le stesse dimensioni di ν, m2/s.

20

4 APPENDICE al capitolo 1

4.1 Atto di moto elementare

Indichiamo con U, V,W le tre componenti della velocita in un riferimentocartesiano x, y, z.Nell’intorno di un punto P qualsiasi, che supporremo si-tuato nell’origine degli assi di riferimento, scriviamo l’espansione in serie diTaylor limitata al primo ordine

U = u+∂u

∂xx+

∂u

∂yy +

∂u

∂zz

V = v +∂v

∂xx+

∂v

∂yy +

∂v

∂zz

W = w +∂w

∂xx+

∂w

∂yy +

∂w

∂zz

dove u, v, w indicano i valori calcolati nell’origine. Notiamo che si puoscrivere in maniera equivalente

U = u+ Ωyz − Ωzy +∆

3x+(

∂u

∂x− ∆

3

)x+

1

2

(∂u

∂y+∂v

∂x

)y +

1

2

(∂u

∂z+∂w

∂x

)z

V = v + Ωzx− Ωxz +∆

3y +

1

2

(∂v

∂x+∂u

∂y

)x+

(∂v

∂y− ∆

3

)y +

1

2

(∂v

∂z+∂w

∂y

)z

W = w + Ωxy − Ωyx+∆

3z +

1

2

(∂w

∂x+∂u

∂z

)x+

1

2

(∂w

∂y+∂v

∂z

)y +

(∂w

∂z− ∆

3

)z

dove ∆ e la divergenza del campo di velocita, data da

∆ =∂u

∂x+∂v

∂y+∂w

∂z(100)

e ~Ω ≡ (Ωx,Ωy,Ωz) rappresenta cinematicamente la velocita istantanea dirotazione di un elemento fluido, grandezza equivalente alla vorticita del flusso~ω ≡ ∇× ~u divisa per due

~Ω ≡ ~ω

2(101)

con

~ω ≡ ∇× ~u ≡(∂w

∂y− ∂v

∂z

∂u

∂z− ∂w

∂x

∂v

∂x− ∂u

∂y

)(102)

21

Notiamo che le componenti

u+ Ωyz − Ωzy

v + Ωzx− Ωxz

w + Ωxy − Ωyx

rappresentano una roto-traslazione rigida locale del punto generico P intornoall’origine O

~u = ~uO + ~Ω× (P −O)

i termini

∆

3x

∆

3y

∆

3z (103)

una dilatazione isotropa, mentre la restante matrice, simmetrica e a traccianulla, puo essere trasformata con una rotazione di coordinate in una matricediagonale sempre a traccia nulla. Il suo significato fisico e quindi quello dirappresentare tre dilatazioni su tre assi ortogonali a volume costante.Essequindi trasformano una sfera in un ellissoide mantenendo costante il volume.

4.2 Streamlines, pathlines, streaklines.

Dato un campo di velocita u(x, y, z, t), v(x, y, z, t), w(x, y, z, t) e spesso mol-to importante determinare quali sono le linee le cui tangenti sono ad essoparallele ad un certo istante, dette linee di corrente o streamlines, le lineeche sono descritte nel loro moto dalle particelle fluide, dette traiettorie opathlines, le linee che vengono ad essere tracciate da un ipotetico coloranteiniettato in punti prefissati, dette streaklines. Per un campo di moto stazio-nario e per un punto prefissato queste tre linee coincidono, mentre per uncampo di moto non stazionario esse sono diverse tra loro tranne casi patolo-gici. Se il campo di moto non e stazionario e inoltre piu corretto parlare dilinee di corrente istantanee, o istantaneous streamlines, essendo quest’ultimevariabili da tempo a tempo.

Un esempio serve a meglio chiarire quanto definito. Consideriamo uncampo di moto le cui componenti cartesiane della velocita sono date rispet-tivamente da

u = axt

v = by

w = 0 (104)

Notiamo che il moto e piano ma non stazionario, e calcoliamo le streamlinesche si hanno al tempo t = 0. Notiamo che non essendo il moto stazionariole streamlines variano da tempo a tempo, e quelle che calcoliamo vengono

22

appunto dette istantaneous streamlines, mentre se il moto fosse stazionarioesse sarebbero le stesse per ogni tempo. Essendo

u =dx

dtv =

dy

dtw =

dz

dt(105)

possiamo anche scrivere che al generico tempo t0 le streamlines istantaneesono descritte dalle equazioni

dx

dσ= axt0

dy

dσ= by

dz

dσ= 0 (106)

con σ coordinata corrente lungo le stesse, (in generale non corrispondentecon l’arco s). Integrando abbiamo

x = x0 exp (at0(σ − σ0))y = y0 exp (b(σ − σ0))z = z0 (107)

dove σ0 indica il valore arbitrario che la coordinata corrente σ assume nelpunto x0, y0, z0 al tempo t0. Notiamo che soltanto se b = at0 la linea dicorrente istantanea e una retta. Calcoliamo ora la traiettoria della particellache al tempo t = t0 si trova nel punto x0, y0, z0. Dobbiamo ora integrare leequazioni del moto nel tempo t

dx

dt= axt

dy

dt= by

dz

dt= 0 (108)

e si ottiene

x = x0 exp

(a

2

(t2 − t20

))y = y0 exp (b(t− t0))z = z0 (109)

4.3 Riepilogo equazioni di bilancio.

Riassumiamo in questa appendice le equazioni di bilancio ottenute a partiredalla teoria cinetica dei gas.Sottolineiamo che sia in questa appendice e siain quelle che seguono, e in generale in tutti gli appunti che seguiranno, lasoprallineatura che indica l’operazione di media sulle fluttuazioni molecolari

23

verra abolita, ed e sottinteso che ogni grandezza e una grandezza media.Inquesta scrittura di riepilogo utilizzeremo inoltre una scrittura piu compatta acarattere tensoriale.Abbiamo allora l’equazione di conservazione della massa

∂%

∂t+∂ (%uj)

∂xj= 0 (110)

l’equazione di bilancio della quantita di moto

∂ (%ui)

∂t+∂ (%uiuj)

∂xj= − ∂p

∂xi+∂τij∂xj

(111)

l’equazione di bilancio dell’energia

∂ (%E)

∂t+∂ (%Huj)

∂xj=∂ (τijui − qj)

∂xj(112)

dove

H = e+p

%+uiui

2(113)

τij = µ

(∂ui∂xj

+∂uj∂xi− 2

3

∂uk∂xk

δij

)(114)

qi = −λ ∂T∂xi

(115)

Notiamo infine che le equazioni di bilancio della quantita di moto possonoessere anche scritte nelle forma Lagrangiana o convettiva

%∂ui∂t

+ %uj∂ui∂xj

= − ∂p

∂xi+∂τij∂xj

(116)

mentre la forma di scrittura precedente e detta forma conservativa.

Riferimenti bibliografici

[1] W.G.Vincenti, C.H.Kruger; Introduction to Physical Gas DynamicsJohn Wiley and Sons, New York (1965)

[2] J.O.Hirschfelder, C.F.Curtiss, R.Byron Bird; The Mathematical Theo-ry of Nonuniform Gases Cambridge University Press, New York(1958)

[3] C.R.Wilke; J.Chem.Phys. Vol.18, pp 517-522, (1950)

[4] W.H.Dorrance; Viscous Hypersonic Flow McGraw-Hill, New York(1962)

[5] H.W.Liepmann, A.Roshko; Elements of Gasdynamics John Wiley andSons, London (1957)

24

APPUNTI DI GASDINAMICA

CAPITOLO 2

STUDIO DELLE EQUAZIONI DI BILANCIO

M. GermanoDip. di Ing. Aeronautica e Spaziale

Politecnico di Torino

1

Indice

1 Il flusso intorno ad un corpo. 3

2 Portanza e resistenza. 7

3 Tipologia dei flussi. 10

4 Equazioni di bilancio 154.1 Equazioni di bilancio in forma vettoriale . . . . . . . . . . . . 154.2 Equazioni di bilancio in forma intrinseca . . . . . . . . . . . . 174.3 Equazioni di bilancio in coordinate ortogonali . . . . . . . . . 194.4 Equazioni di bilancio in coordinate cartesiane . . . . . . . . . 234.5 Equazioni di bilancio in coordinate cilindriche . . . . . . . . . 24

5 Flussi di punta 26

6 Flussi di taglio piani 30

7 Flussi di taglio cilindrici 337.1 Flusso nei tubi . . . . . . . . . . . . . . . . . . . . . . . . . . 357.2 Vortice lineare . . . . . . . . . . . . . . . . . . . . . . . . . . 357.3 Vortice di Rankine . . . . . . . . . . . . . . . . . . . . . . . . 367.4 Vortice lineare compressibile . . . . . . . . . . . . . . . . . . . 377.5 Vortice di Rankine compressibile . . . . . . . . . . . . . . . . 38

8 Flussi rotazionali inviscidi 398.1 Materialita di punti, linee e superfici . . . . . . . . . . . . . . 408.2 Equazione di Helmoltz. Dinamica della vorticita. . . . . . . . 42

9 Flussi di strato limite. 439.1 Strati limite self similari . . . . . . . . . . . . . . . . . . . . . 46

2

1 Il flusso intorno ad un corpo.

Considerazioni dimensionali fanno dipendere l’azione esercitata da un fluidosu di un corpo dall’angolo di incidenza α e dai numeri di Mach Ma e diReynolds Re calcolati sulla base di una lunghezza caratteristica del corpo Le delle proprieta della corrente indisturbata %, c, U e µ

Ma =U

cRe =

%UL

µ

Le variazioni che il flusso assume intorno al corpo al variare dei parametriα, Ma e Re sono notevoli. Lo strato limite che lambisce il corpo puo esserelaminare o turbolento, si possono manifestare distacchi o onde d’urto, ilflusso puo restare stazionario o diventare caotico con emissione di vorticinel tempo. Tutto cio ha grandi conseguenze sui valori della portanza edella resistenza, le cui cause fisiche, e cioe gli sforzi d’attrito a parete, lanascita di separazioni della corrente e di onde d’urto, l’emissione di vorticita,sono spesso intrecciate tra loro. Ricordiamo che la portanza si esercitanormalmente alla direzione della corrente indisturbata, e ad essa quindicorrisponde, come effetto reattivo sul fluido, una variazione di quantita dimoto normale alla direzione del flusso indisturbato. La portanza sostienema non lavora, al contrario della resistenza che proviene da una diminuzionedella quantita di moto parallelamente alla direzione del flusso indisturbato.Dal punto di vista fisico e inoltre importante sottolineare che per una dataincidenza si hanno nel piano Ma,Re due zone nettamente distinte, quellain cui vale l’ipotesi del continuo e il gas che investe il corpo puo essererappresentato attraverso le equazioni di bilancio di Navier-Stokes, e quellain cui il gas si presenta cosı rarefatto al corpo da imporre una trattazionecompletamente diversa delle azioni meccaniche scambiate tra il corpo e lostesso. Ricordiamo infatti che la viscosita µ e fisicamente legata alla velocitadi agitazione termica vat e al libero cammino medio l dalla relazione

µ ' %vatl

e che la velocita del suono e dello stesso ordine di grandezza della velocita diagitazione termica, cioe della velocita con cui, attraverso gli urti, si propagal’informazione. Si ottiene allora

Ma

Re' Kn =

l

L(1)

il che significa che la retta Ma = Re separa, vedi figura (1), due zone netta-mente distinte, quella del continuo Ma < Re da quella del rarefatto Ma > Re.La distinzione ovviamente non e cosı netta, e passa attraverso zone interme-die dette di slip-flow, Kn > 0.01, di leggera rarefazione, di moderata rarefa-zione e infine di alta rarefazione, (regime di molecole libere), per Kn > 10,

3

e notiamo il grande interesse aerospaziale di questi regimi di flusso che so-no tipici della mesosfera e della termosfera, cioe di moti in quote superioriall’incirca ai 50 km di altezza.

La complessita del panorama continua a rimanere molto grande anchese ci si limita a considerare cio che avviene intorno ad un corpo di dimen-sione caratteristica L dell’ordine di un metro e investito da una correntedi aria standard, (p = 1.01325 · 105N/m2, % = 1.2250kg/m3, T = 288.2K,c = 340m/s, µ = 1.79 · 10−5kg/m/s). In tal caso il numero di Knudsene dell’ordine di 10−7 e a variazioni della corrente esterna tra valori dell’or-dine di un metro al secondo e valori dell’ordine di 1000 metri al secondocorrispondono variazioni del numero di Reynolds tra 105 e 108 e variazionidel numero di Mach tra 0 e 3. Supponiamo innanzitutto che il corpo siauna lamina piana bidimensionale, un caratteristico corpo portante, nel qualecioe la portanza e esaltata rispetto alla resistenza da una notevole snellezzae da una notevole bidimensionalita nei confronti della corrente indisturbata.Seguiremo l’evoluzione del flusso sia dal punto di vista teorico che da quellosperimentale. Da un lato abbiamo la realta quale ci si presenta attraversole prove in galleria, le visualizzazioni, le misure delle varie grandezze. Dal-l’altra abbiamo le equazioni che questa realta descrivono e le cui soluzioni,generalmente molto difficili da ottenere, vanno interpretate con molta curae con molto buonsenso fisico-matematico. Partiamo quindi dalla lamina adincidenza nulla, α = 0, Re = 105 e Ma ' 0. Le equazioni di Eulero fornisco-no in questo caso un risultato semplicissimo e banale, a patto di rinunciarealla condizione di aderenza a parete: il flusso resta del tutto indisturbatoe l’azione sul corpo e nulla. In realta la velocita del fluido a parete deveannullarsi: la soluzione matematica trovata andrebbe bene se il corpo fosseprovvisto di rulli la cui velocita periferica fosse la stessa del fluido esterno,vedi figura (2). Fermiamo allora i rulli. Dal punto di vista delle equazionicio significa sovrapporre alla soluzione di prima il calcolo dello strato limitein vicinanza di parete. Questo sdoppiamento in due fasi del calcolo, (calcolodel flusso potenziale esterno su di un corpo con rulli, fermata dei rulli ecalcolo di strato limite sovrapposto), sdoppiamento che puo raffinarsi in unatecnica iterativa, e tanto piu giustificato quanto piu lo strato limite si riducead una guaina sottile aderente al corpo. Indichiamo con x la coordinatacorrente lungo il corpo a partire dal bordo d’attacco, con y la coordinatanormale al corpo stesso e con δ lo spessore dello strato limite, intendendoper il momento con questo termine l’estensione della zona di influenza deitermini viscosi. Notiamo che lo sforzo viscoso principale τxy e scalato co-me µU/δ, e un semplice bilancio tra le forze d’inerzia esterne per unita divolume

∂ (%uu)

∂x

4

scalate come

%U2

L

e le forze viscose per unita di volume

∂τxy∂y

scalate come

µU

δ2

fornisce per lo spessore dello strato limite laminare la stima

δ

L' 1√

Re(2)

il che porta per i numeri di Reynolds considerati a spessori dell’ordine dipochi millimetri. Cio determina tuttavia tre conseguenze : la nascita di unosforzo τp d’attrito a parete dell’ordine di

τp = (τxy)y=0 = µ

(∂u

∂y

)y=0

' µUδ

che integrato su tutta la lamina da la resistenza d’attrito, la produzione diuna scia in cui si cicatrizza la perdita di quantita di moto operata sul fluidoindisturbato dalla fermata dei rulli, lo spostamento verso l’esterno del flussopotenziale e il relativo ispessimento del corpo che si presenta come gonfiatorispetto alla sua forma di partenza, vedi figura (3). Al fine di valutare intutta la sua importanza questo fatto facciamo subito un salto di velocita eportiamoci di colpo in questo assetto a Ma = 3; l’effetto dell’ispessimentodovuto allo strato limite e quello di far nascere una onda d’urto a poppadella lamina stessa, vedi figura (4). Notiamo anche che nello strato limite epiu opportuno scalare il numero di Knudsen non con L, dimensione caratte-ristica del corpo, ma con δ, spessore dello strato limite stesso. Cio aumentaconsiderevolmente il campo in cui si manifestano gli effetti di rarefazione delgas, vedi figura (1). Abbiamo infatti

Knδ =l

δKnL =

l

L

e quindi

Knδ = KnLL

δ' Ma√

Re(3)

il che dimostra che per esempio a Mach 10 e a Reynolds 100 lo spessore dellostrato limite δ e dello stesso ordine di grandezza del libero cammino mediomolecolare l. Facciamo ora variare l’incidenza α. Nuovamente esaminiamo

5

la soluzione piu semplice delle equazioni, sempre interpretabile come soluzio-ne su di un corpo provvisto di rulli, vedi figura (5). La soluzione potenziale,dappertutto irrotazionale e senza vorticita aderente al corpo, quella cioe cheavvolge il corpo con il minimo disturbo, e in netto contrasto con l’esperienza.Notiamo che l’effetto di questo campo di moto sul corpo e nullo come forza:niente portanza, niente resistenza e si riduce ad una sola coppia che tende ametterlo in bandiera, (paradosso di D’Alembert). In questo caso non bastasovrapporre un calcolo di strato limite per aggiustare le cose. Il male e piuprofondo e va curato fermando prima certi rulli in modo da ottenere unanuova soluzione potenziale esterna piu aderente alla realta. Cio va d’accordocon la matematica che fornisce in questo caso tutta una famiglia di soluzionicorrispondente ai rulli che vogliamo fermare. Per basse incidenze il rulloche certamente va fermato per primo al fine di riacquistare una certa corri-spondenza con la realta e quello di coda che come si puo vedere e quello piusollecitato e meno corrispondente alla realta fisica. Questo rullo sta infattiruotando a velocita infinita e trascina con se tutto il flusso che teoricamentesi dovrebbe riavvolgere sulla lamina ma che praticamente si separa. Fermarequesto rullo vuol dire matematicamente applicare la condizione di Kutta, edabbiamo la nuova soluzione di figura (6), che determina sul flusso una varia-zione di quantita di moto normalmente al vento, e quindi una sola portanza:il fluido interviene ora piu pesantemente sul corpo, e dalla coppia si passaad una forza, ma ad una forza che non lavora. Cio e dovuto essenzialmentead un vortice che aderisce e si concatena alla lamina, (nel subsonico si volaappesi ad un vortice), e che si sviluppa durante la fase di avviamento. Que-sto vortice puo essere pero perduto all’aumentare dell’incidenza, in quantosu di un altro rullo si sviluppano gradualmente all’aumentare dell’incidenzaα velocita rotatorie sempre piu insostenibili, vedi figura (7). Cio che avvienenella realta e che anch’esso a un certo punto si ferma e non assicura piu ilriavvolgimento a prua: la lamina stalla e perde il vortice che la sostenevagenerando una scia di flusso separato la cui determinazione esatta e uno deicompiti piu delicati del calcolo aerodinamico. In questa sequenza di eventiil calcolo di strato limite viene ad assumere un ruolo quasi secondario, fon-damentale nel determinare la resistenza d’attrito sul corpo e quindi il lavorofatto per trascinarlo nella corrente indisturbata, ma semplice nella tecnica diesecuzione. Dato il flusso esterno si tratta di sovrapporre ad esso uno stratolimite ottenuto fermando ora tutti i rulli, ma dopo che la soluzione esternapiu aderente dal punto di vista fisico e stata trovata. Sottolineiamo inoltrela caratteristica peculiare della viscosita : essa assicura l’aderenza a parete,determina gli sforzi di attrito, ma non altera minimamente il valore dellavorticita che a partire dall’avviamento impulsivo si e concatenata al corpo.I fenomeni viscosi sono fenomeni puramente diffusivi e sotto questo punto divista la viscosita semplicemente spalma sullo strato limite la discontinuitadi velocita a parete.

6

Saltiamo a pie pari il transonico la cui complessita ed importanza meri-ta una trattazione troppo particolareggiata per questo rapido sguardo d’in-sieme e vediamo che cosa succede sulla nostra lamina nel supersonico conincidenza, in quanto quello che avviene ad α = 0 e stato gia visto in pre-cedenza. Cio che avviene e che cambiano radicalmente i meccanismi chegenerano portanza e resistenza sul corpo. Se nel subsonico era lecito direche si volava aggrappati ad un vortice ora e lecito dire che si vola sopra diun’onda. Da figura (8) vediamo infatti che nasce un’onda d’urto che assicuraun’aumento di pressione sulla parte di lamina esposta al vento mentre unfascio di onde di rarefazione mette in depressione la parte controventata. Laresistenza d’onda interviene ora nel computo della resistenza totale, il chetuttavia non toglie importanza al calcolo dello strato limite anche perche inesso diventano sempre piu importanti le dissipazioni d’energia da cinetica atermica, con graduale aumento delle temperature e dei carichi termici sullestrutture. E’ importante comunque notare che nel supersonico non c’e por-tanza senza resistenza in quanto la forza agente e diretta normalmente allalamina e non, come nel subsonico, normalmente al vento. I vortici e le onded’urto sono creati dai moti impulsivi, e la loro determinazione puo esserefatta senza considerare affatto i fenomeni viscosi o la conduzione termica.L’aerodinamica subsonica riesce a determinare la vorticita che aderisce ad uncorpo sulla base di semplici condizioni relative alla posizione dei punti d’ar-resto, (condizioni di Kutta). L’aerodinamica supersonica riesce a calcolarele condizioni di flusso attraverso un urto retto semplicemente considerandolocome una discontinuita. In effetti sia l’urto retto che lo scorrimento vortico-so che si stabilisce su di un corpo vengono diffusi da viscosita e conducibilitatermica. L’urto ha uno spessore viscoso e sui corpi si formano degli stratilimite. Allo scopo di chiarire il ruolo che viscosita e conducibilita termicahanno sul moto consideriamo infine un corpo riscaldato, messo in moto elasciato libero a se stesso in assenza di forze esterne. Esso possiede una certaquantita di moto ed una certa energia termica. La viscosita e la conducibi-lita termica permettono che il corpo scambi queste grandezze con il mondoesterno diffondendole nell’aria circostante. Come conseguenza il corpo tendea portarsi alla stessa velocita e temperatura dell’aria esterna ma la quantitadi moto e l’energia totale del sistema corpo-aria resteranno le stesse.

2 Portanza e resistenza.

Vediamo ora piu in dettaglio sotto quali forme tipiche puo presentarsi laresistenza offerta da un corpo all’avanzamento in un fluido. Notiamo chela conoscenza dettagliata delle pressioni e degli sforzi a parete permette ladeterminazione della forza esercitata da un fluido su di un corpo e del suomomento rispetto ad un punto dato. Viene chiamata resistenza la com-

7

ponente della forza diretta parallelamente al moto, forza deviatrice quellanormale. La portanza e una forza deviatrice.

I cofficienti di portanza CL e di resistenza CD sono definiti sulla basedi una opportuna superficie di riferimento S. Se con L e D indichiamorispettivamente la portanza e la resistenza che un fluido esercita su di uncorpo, allora abbiamo

CL =L

1

2%∞U

2∞S

CD =D

1

2%∞U

2∞S

(4)

dove %∞ e U∞ sono i valori della densita e della velocita della correnteindisturbata. Per quel che riguarda la superficie di riferimento S occorrefare bene attenzione a come essa e definita. Tipicamente abbiamo tre diversepossibilita: la sezione maestra, la superficie in pianta, la superficie bagnata.La superficie in pianta e preferita per corpi aerodinamici, per corpi tozzi ilcoefficiente di resistenza e comunemente riferito alla sezione maestra, mentrela superficie bagnata e normalmente usata quando si parla di pura resistenzadi attrito.

La portanza e essenzialmente dovuta alle forze di pressione, esercitatenormalmente al corpo. La parte di resistenza dovuta alle pressioni vienechiamata resistenza di scia, o di forma, o di pressione mentre quella dovutaagli sforzi viscosi e detta resistenza d’attrito. Per flussi supersonici si distin-gue tra resistenza di scia e resistenza d’onda. Si riserva il nome di resistenzaindotta a quella che risulta dalla generazione di una scia portante ed altritermini vengono alle volte usati per evidenziare aspetti particolari. Vienequindi chiamata resistenza interferenziale quella che risulta mettendo duecorpi in prossimita l’uno dell’altro, resistenza di base quella che proviene dalbrusco troncamento della coda di un corpo aerodinamico, e cosı via.

Notiamo che queste definizioni sono alle volte abbastanza vaghe e vannoesaminate caso per caso. Per flussi subsonici la distinzione tra resistenza discia e di attrito e forse la piu precisa anche perche per alti numeri di Rey-nolds i relativi metodi di calcolo sono ben distinti. Ricordiamo infatti chel’aerodinamica dei flussi irrotazionali permette di ricavare il flusso esterno,mentre la teoria di strato limite permette di calcolare la resistenza di attrito.Per corpi aerodinamici la resistenza di attrito e la piu importante. La resi-stenza di un aereo e tipicamente formata per meta da resistenza di attritoe per un quarto da resistenza indotta. Cio spiega la grande importanza cheil calcolo della resistenza d’attrito riveste in un corso dedicato alle appli-cazioni aeronautiche, ma non deve far dimenticare che in altre applicazionila resistenza di forma e largamente predominante. Un altro punto che vasottolineato e che mentre il calcolo della portanza e della resistenza d’attritohanno raggiunto un certo grado di affidabilita, il calcolo della resistenza discia presenta spesso problemi di difficile risoluzione. Cio e dovuto al fattoche la resistenza di scia e dovuta generalmente ad impianti vorticosi liberi di

8

geometria molto complessa e spesso variabile caoticamente nel tempo. Dalpunto di vista teorico lo studio della resistenza di scia e intimamente legatoallo studio delle dinamica della vorticita, cioe dei flussi inviscidi ma rotazio-nali. Questi flussi nascono normalmente intorno a corpi tozzi o intorno acorpi aerodinamici ad alta incidenza. In questi casi sul corpo si hanno sepa-razioni dalle quali si generano strati vorticosi che evolvendo nella correntedeterminano scie resistenti.

Per la determinazione della resistenza di scia e fondamentale l’esperienzadi galleria del vento. I dati ottenuti su modelli vengono scalati al veronotando che la resistenza di scia e largamente indipendente dal numerodi Reynolds essendo un fenomeno peculiarmente inerziale. Naturalmentelo strato limite, che dipende dal numero di Reynolds, ha il suo ruolo nelladeterminazione della scia, soprattutto per quel che riguarda la localizzazionedelle separazioni, anticipate se il flusso e laminare, posticipate se il flussoe turbolento. Questa interferenza tra strati limite e scie complica molto lecose, ma spesso e possibile dare un idea abbastanza precisa di quello cheavviene al di sopra di un certo numero di Reynolds critico sulla base disole tabelle sperimentali. In figura (9) si riportano alcuni dati relativi allaresistenza di scia di corpi semplici. E’ importante notare la forte caduta diresistenza per cilindro e sfera intorno ad un numero di Reynolds di 200000.In entrambi i casi la causa e dovuta ad un maggiore avvolgimento dellascia conseguente ad una separazione piu ritardata dello strato limite. Altrodato interessante e quello relativo al cilindro a sezione quadra : il valore 2per il CD significa sostanzialmente che il flusso di quantita di moto bloccatodal corpo e esttamente quello intercettato dalla sezione maestra. Questorisultato sarebbe elementarmente ricavabile con la teoria dell’impatto diNewton, ma ricordiamo le disastrose conseguenze che ebbe sulla teoria delvolo la sua estensione a lamine piane con bassa incidenza . . . . . In realtachi produce la portanza sono i vortici e chi produce la resistenza pure. Infigura (10) si illustrano le due tipiche configurazioni di scia vorticosa portantee di scia vorticosa resistente. Nel primo caso la scia e schematizzabile in unanello vorticoso con asse normale alla direzione del moto. Per la legge diBiot e Savart esso risucchia aria verso il basso e quindi reagisce sul corpo conuna portanza. Nel secondo caso il corpo genera dietro di se tutta una serie dianelli vorticosi ad asse parallelo al moto. Sempre per la legge di Biot e Savartquesto solenoide percorso da correnti vorticose genera un campo di motoparallelo alla direzione di avanzamento e determina sul corpo una resistenza.Si segnalano infine due testi ottimi per quel che riguarda una consultazionerapida ed abbastanza esauriente riguardante i coefficienti di resistenza sianel subsonico che nel supersonico. Essi sono il libro del Rebuffet [1] e quellodel McCormick [2]. In particolare si raccomanda quest’ultimo come quellopiu orientato verso le applicazioni aeronautiche.

9

3 Tipologia dei flussi.

Dopo queste considerazioni di carattere generale relative sia alla fenomenolo-gia del flusso intorno ad un corpo investito da una corrente, sia alle grandezzedi principale interesse aeronautico, la portanza e la resistenza, vediamo oracome tutto cio si possa leggere e calcolare in chiave matematica. Scriviamoinnanzitutto le equazioni relative al moto di un flusso piano, bidimensionalee incompressibile, cioe con densita % costante. Le componenti della velocitasono allora date da

u = u (x, y, t) v = v (x, y, t) w = 0

e ricordiamo che la condizione di incompressibilita puo essere dovuta sia aduna condizione piezotropica, (% e costante in quanto questa e una precisacondizione di stato del fluido considerato, per esempio l’acqua), sia ad unacondizione barotropica, (ricordiamo infatti dal corso di Termofluidodinamicache un flusso puo essere considerato a % costante se il numero di Mach esufficientemente basso)

∆%

%≈Ma2

Abbiamo allora∂u

∂x+∂v

∂y= 0

%∂u

∂t+ %u

∂u

∂x+ %v

∂u

∂y= −∂p

∂x+ fx

%∂v

∂t+ %u

∂v

∂x+ %v

∂v

∂y= −∂p

∂y+ fy (5)

dove le componenti della forza viscosa f per unita di volume sono date da

fx =∂τxx∂x

+∂τxy∂y

fy =∂τxy∂x

+∂τyy∂y

(6)

In condizioni di incompressibilita gli sforzi viscosi sono dati dalle relazioni

τxx = 2µ∂u

∂xτxy = µ

(∂u

∂y+∂v

∂x

)τyy = 2µ

∂v

∂y(7)

e si ottiene con semplici passaggi la scrittura delle equazioni di bilancio sottola forma

∂u

∂x+∂v

∂y= 0

%∂u

∂t+ %u

∂u

∂x+ %v

∂u

∂y= −∂p

∂x+ µ

(∂2u

∂x2+∂2u

∂y2

)

%∂v

∂t+ %u

∂v

∂x+ %v

∂v

∂y= −∂p

∂y+ µ

(∂2v

∂x2+∂2v

∂y2

)(8)

10

Calcoliamo ora la vorticita ω ≡ (ωx, ωy, ωz) del flusso piano considerato. Siha

ωx = ωy = 0 ωz =∂v

∂x− ∂u

∂y(9)

E’ interessante notare che se deriviamo la seconda equazione delle (8) lungo ye la terza lungo x otteniamo una equazione evolutiva per ωz detta equazionedi Helmoltz

∂ωz∂t

+ u∂ωz∂x

+ v∂ωz∂y

= ν

(∂2ωz∂x2

+∂2ωz∂y2

)(10)

dove si e introdotta la viscosita cinematica ν = µ/%, mentre se deriviamola seconda equazione delle (8) lungo x e la terza lungo y otteniamo unaequazione per p

∂2p

∂x2+∂2p

∂y2= 2%

(∂u

∂x

∂v

∂y− ∂u

∂y

∂v

∂x

)(11)

Notiamo due importanti particolarita della (10) e della (11). La prima, chedescrive l’evoluzione della vorticita, non dipende esplicitamente dal campodi pressioni, mentre la seconda, utile per determinare il campo di pressioninoto il campo di velocita, non dipende esplicitamente dalla viscosita.

Consideriamo ora flussi stazionari, per i quali le derivate temporali sononulle, e introduciamo la pressione totale P

P = p+ %u2 + v2

2(12)

E’ facile controllare che nei termini di P e di ωz le (8) possono essere scrittenella forma alternativa equivalente

∂u

∂x+∂v

∂y= 0

∂P

∂x= %vωz − µ

∂ωz∂y

∂P

∂y= − %uωz + µ

∂ωz∂x

(13)

che si presta ad una interessante lettura. Notiamo subito che esse ammettonole soluzioni irrotazionali date da

∂u

∂x+∂v

∂y= 0

∂v

∂x− ∂u

∂y= ωz = 0 (14)

che comportano come immediata conseguenza la conservazione dappertuttodella pressione d’arresto P

P = p+ %u2 + v2

2= costante dappertutto (15)

11

risultando

∂P

∂x=∂P

∂y= 0 (16)

Facciamo presente che le componenti della velocita u e v sono in questo casoricavabili come gradiente di un potenziale ϕ

u =∂ϕ

∂xv =

∂ϕ

∂y(17)

che soddisfa l’equazione

∂2ϕ

∂x2+∂2ϕ

∂y2= 0 (18)

il che da a questi flussi anche il nome di flussi potenziali, e sottolineiamo ilfatto che se ωz = 0 le forze viscose sono automaticamente nulle, (non cosıgli sforzi !).

Vediamo ora di esaminare gli ordini di grandezza dei vari termini delleequazioni di bilancio. E’ fondamentale a questo proposito distinguere traflusso esterno e flusso nelle vicinanze delle pareti, o flusso di strato limite.Nel caso di flussi esterni possiamo scalare entrambe le componenti dellavelocita u e v con U , velocita della corrente indisturbata, ed entrambe ledistanze x e y con L, dimensione caratteristica del corpo,

u ≈ U v ≈ U x ≈ L y ≈ L (19)

mentre la pressione p e dimensionalmente scalata con %U2. Abbiamo alloradalle equazioni di bilancio (8)

%u∂u

∂x+ %v

∂u

∂y= −∂p

∂x+ µ

∂2u

∂x2+ µ

∂2u

∂y2

%U2

L

%U2

L

%U2

L

1

Re

%U2

L

1

Re

%U2

L

%u∂v

∂x+ %v

∂v

∂y= −∂p

∂y+ µ

∂2v

∂x2+ µ

∂2v

∂y2

%U2

L

%U2

L

%U2

L

1

Re

%U2

L

1

Re

%U2

L

dove ai vari termini sono sottoposti gli ordini di grandezza e da cui si deduceche per

Re =%UL

µ>> 1 (20)

12

le forze viscose possono essere trascurate nel flusso esterno. Cio pero nonvuol dire automaticamente che il flusso sia irrotazionale. In generale avremo

∂u

∂x+∂v

∂y= 0

∂P

∂x= %vωz

∂P

∂y= −%uωz (21)

equazioni che regolano i flussi piani non viscosi ma rotazionali, ωz 6= 0. Inpratica essi si incontrano essenzialmente come flussi di scia, flussi esternimarchiati da un precedente passaggio in vicinanza di corpi, (per esempiol’ala), che ha impartito ad essi rotazionalita, e che si apprestano come flussiesterni rotazionali ad investire altri corpi, (per esempio i piani di coda).Questi flussi sono caratterizzati dal fatto che per essi la pressione d’arrestoP non e piu costante. Notiamo tuttavia che dalle equazioni di bilancio siricava ugualmente l’importante risultato

u∂P

∂x+ v

∂P

∂y= 0 (22)

che informa della conservazione di P non piu dappertutto ma ancora lungole linee di corrente, con valore tuttavia diverso dall’una all’altra. Abbiamocioe un teorema di Bernoulli ridotto a

P = p+ %u2 + v2

2= costante su di una linea di corrente (23)

che ancora puo essere di grande utilita nelle applicazioni. E’ interessanteinfine notare che dalla equazione di Helmoltz (10)

u∂ωz∂x

+ v∂ωz∂y

= ν

(∂2ωz∂x2

+∂2ωz∂y2

)(24)

si ricava l’importantissimo risultato che in assenza di effetti diffusivi viscosianche la vorticita ωz si conserva su di una linea di corrente

u∂ωz∂x

+ v∂ωz∂y

= 0 (25)

Cogliamo l’occasione per ribadire il fatto che la viscosita non crea vorticitama semplicemente la diffonde. La vorticita e creata dai moti impulsivi iner-ziali, e il ruolo della viscosita e semplicemente quello di diffonderla quantopiu puo compatibilmente con i moti convettivi. Notiamo che nel calcolodegli sforzi essa si presenta come µ, mentre a livello diffusivo i suoi effettisone meglio scalati come ν, viscosita cinematica. La differenza tra le pro-prieta fisiche dell’aria e dell’acqua puo chiarire meglio questo aspetto. Laviscosita µ dell’acqua e circa 100 volte maggiore di quella dell’aria, e quindi

13

a parita di gradiente di velocita di taglio lo sforzo viscoso e in acqua 100volte maggiore. La densita dell’acqua e pero circa 1000 volte maggiore diquella dell’aria, e quindi la viscosita cinematica ν dell’aria viene ad esserecirca di 10 volte maggiore di quella dell’acqua. Cio vuol dire che la vorticitadiffonde in aria molto piu rapidamente che nell’acqua.

Vediamo ora di analizzare i flussi di strato limite. Abbiamo visto cheessi avvolgono i corpi con spessori δ molto piccoli rispetto alla dimensionecaratteristica del corpo L se Re >> 1, il che permette la loro trattazionein una geometria semplificata, nella quale la distanza x e quella misuratalungo il corpo a partire dal punto di arresto ed y la distanza dalla parete,vedi figura (11), e contrariamente ai flussi esterni non possiamo piu supporreche esse siano scalate nello stesso modo. La stessa considerazione va fattaper le componenti u e v di velocita, (rispettivamente quella lungo il corpo equalla normale ad esso), per cui avremo piu correttamente

u ≈ U x ≈ L y ≈ δ p ≈ %U2 (26)

mentre dalla equazione di continuita ricaviamo l’ordine di grandezza di vdato da

v ≈ U δ

L(27)

Sulla base dell’analisi degli ordini di grandezza dei singoli termini deriveremoora le equazioni dello strato limite. Come nel caso dell’analisi fatta sul flussoesterno scriviamo

%u∂u

∂x+ %v

∂u

∂y= −∂p

∂x+ µ

∂2u

∂x2+ µ

∂2u

∂y2

%U2

L

%U2

L

%U2

L

1

Re

%U2

L

1

Re

%U2

L

(L

δ

)2

%u∂v

∂x+ %v

∂v

∂y= −∂p

∂y+ µ

∂2v

∂x2+ µ

∂2v

∂y2

%U2

L

(δ

L

)%U2

L

(δ

L

)%U2

L

(L

δ

)1

Re

%U2

L

(δ

L

)1

Re

%U2

L

(L

δ

)sottoponendo ai vari termini i rispettivi ordini di grandezza. Se ora liesaminiamo tenendo conto del fatto che

δ

L<< 1

δ

L≈ 1√

Re(28)

come visto in precedenza, allora l’equazione di bilancio della quantita dimoto lungo la direzione y normale alla parete si riduce a

∂p

∂y= 0 (29)

14

il che avverte che nello strato limite non c’e alcun recupero di pressione.Questo fatto fondamentale che caratterizza i flussi di strato limite permettedi porre in esso

p = pe(x) (30)

dove pe(x) e la pressione ad esso esterna, generalmente provvista da unasoluzione di flusso esterno. Vediamo ora cosa avviene lungo la direzione xcorrente lungo il corpo. Nella relativa equazione di bilancio della quantita

di moto puo essere ora trascurato il termine µ∂2u

∂x2e inoltre si puo porre in

essa∂p

∂x=dpedx

. Abbiamo quindi

∂u

∂x+∂v

∂y= 0 (31)

%u∂u

∂x+ %v

∂u

∂y= −dpe

dx+ µ

∂2u

∂y2(32)

equazioni dello strato limite bidimensionale, incompressibile, stazionario. E’interessante stimare nello strato limite anche l’ordine di grandezza sia dellavorticita ωz sia della pressione d’arresto P . Avendosi, come in precedenza,dalla equazione di continuita v ≈ Uδ/L, si ottiene

ωz =∂v

∂x− ∂u

∂y; P = p + %

u2

2+ %

v2

2

Uδ

L2

U

δ%U2 %U2 %U2

(δ

L

)2

il che permette di scrivere nello strato limite con buona approssimazione

ωz = −∂u∂y

P = p+ %u2

2(33)

In figura (12) vengono riassunti ed illustrati graficamente i principali puntiesposti in questa sezione.

4 Equazioni di bilancio

4.1 Equazioni di bilancio in forma vettoriale

Vediamo ora di generalizzare quanto detto sopra al caso tridimensionale. E’facile controllare innanzitutto che le equazioni di bilancio

∂%

∂t+ uj

∂%

∂xj+ %

∂uj∂xj

= 0

15

%∂ui∂t

+ %uj∂ui∂xj

= − ∂p

∂xi+∂τij∂xj

(34)

dove

τij = µ

(∂ui∂xj

+∂uj∂xi− 2

3

∂uk∂xk

δij

)(35)

possono essere scritte sotto la forma vettoriale

∂%

∂t+ u · ∇%+ %∇ · u = 0

%∂u

∂t+ %u · ∇u = −∇p+ f (36)

dove f rappresenta la forza viscosa. L’espressione vettoriale della forza visco-sa e abbastanza complessa. Per flussi incompressibili e per viscosita costantee facile tuttavia controllare che essa si riduce all’espressione

f = −µ∇× ω (37)

come si puo facilmente verificare. Vediamo quindi che come gli sforzi viscosianche la forza viscosa non dipende direttamente dalla vorticita, (il doppiodella velocita istantanea di rotazione di un elementino fluido), ma dal ro-tore della vorticita, ed e quindi nulla in ogni caso in un campo di motoirrotazionale. Se ora facciamo uso della identita vettoriale

u · ∇u = ω × u +∇(

u · u2

)(38)

possiamo scrivere l’equazione di bilancio della quantita di moto sotto laforma

%∂u

∂t+ %ω × u = −∇

(p+ %

u · u2

)+ f (39)

Notiamo ora che se il fluido considerato e incompressibile, % = costante, ese si trascurano le forze viscose, si puo ricavare direttamente da quest’ultimaequazione sia il teorema di Bernoulli sotto la sola condizione di stazionarietae di irrotazionalita del flusso

p+ %u · u

2= costante dappertutto (40)

sia la relazione piu restrittiva ma condizionata dalla sola stazionarieta delfluido

p+ %u · u

2= costante su di una linea di corrente (41)

ottenuta moltiplicando scalarmente l’equazione di bilancio della quantita dimoto per u.

16

4.2 Equazioni di bilancio in forma intrinseca

Finora abbiamo scritto le equazioni di bilancio in un sistema di riferimentoCartesiano, tale cioe che la metrica delle coordinate scelte e data da

dP · dP = dx2 + dy2 + dz2

dove il vettore dP rappresenta la distanza infinitesima tra due punti nellospazio. La scrittura in forma vettoriale ci ha affrancati da questa condizione,e notiamo che un’altra forma di scrittura delle equazioni di bilancio parti-colarmente sintetica ed utile e quella intrinseca. Il sistema di riferimentointrinseco e quello in cui ad ogni punto dello spazio viene istantaneamenteassociata la terna fondamentale di versori τ ,n,b, rispettivamente la tan-gente, la normale e la binormale alla traiettoria passante per quel punto, vedifig. (13). L’espressione della velocita nel sistema intrinseco di coordinate eovviamente molto semplice. Essa e data da

u = qτ (42)

dove q e il modulo della velocita, ma cio non deve trarre in inganno perchein realta il sistema intrinseco di riferimento e un sistema molto difficile datrattare. Si dimostra infatti che esso e un sistema locale, nel senso che senoi ad un certo istante tracciamo le τ -linee, (le traiettorie), le n-linee ele b-linee le coordinate d’arco, cioe le distanze calcolate lungo queste lineea partire da un punto origine O dipendono dal come si arriva al punto P ,vedi fig. (14), il che ovviamente impedisce di associare univocamente adogni punto una precisa terna di coordinate. Ciononostante la scrittura delleequazioni di bilancio in questo sistema locale e molto utile. Notiamo alloscopo che la derivazione lungo le linee coordinate puo essere formalmentescritta come

τ · ∇ =∂

∂sn · ∇ =

∂

∂nb · ∇ =

∂

∂b

e sottolineiamo subito il fatto che queste derivate formali vanno trattatecon molta cautela. A titolo di esempio mettiamo in guardia che non egeneralmente vero che

∂2

∂s∂n=

∂2

∂n∂s

essendo in generale

τ · ∇(n · ∇) 6= n · ∇(τ · ∇)

Ricordiamo ora le relazioni del Frenet che ci dicono come variano i versorifondamentali lungo la linea di corrente s

∂τ

∂s=

n

R

17

∂n

∂s=

b

ϑ− τR

∂b

∂s= −n

ϑ(43)

e introducono il raggio di curvatura R(s) e di torsione ϑ(s) della linea stessa,funzioni in generale dell’arco s. Se ora proiettiamo la vorticita sulla ternafondamentale otteniamo

ω = ωsτ + ωnn + ωbb

e notiamo che alla componente ωs lungo la linea di corrente e dato il nomedi vorticita secondaria. E’ facile ricavare le espressioni delle due componentilungo la normale e la binormale della vorticita. La solita identita vettoriale

u · ∇u = ω × u +∇(

u · u2

)scritta nel riferimento intrinseco assume infatti la forma

q∂u

∂s= ∇q

2

2− qωnb + qωbn

e quindi

qτ∂q

∂s+ q2

∂τ

∂s= ∇q

2

2− qωnb + qωbn

Proiettando ora questa equazione sulle direzioni n e b si ottengono le rela-zioni volute

ωn =∂q

∂bωb =

q

R− ∂q

∂n(44)

con R raggio di curvatura locale della linea di corrente.Vediamo ora quale forma assumono le equazioni di bilancio in questo

sistema di coordinate. Consideriamo flussi stazionari e inviscidi e indichiamocon A la sezione di un tubicino di flusso avente per asse una linea di corrente,(ricordiamo che una s-linea e una traiettoria e che per flussi stazionari letraiettorie diventano linee di corrente). L’equazione di bilancio della massada ovviamente

∂(%qA)

∂s= 0 (45)

e se proiettiamo l’equazione di bilancio della quantita di moto nella sua formastazionaria sulle tre direzioni τ ,n,b otteniamo, per flussi incompressibili

q∂q

∂s= −1

%

∂p

∂s

q2

R= −1

%

∂p

∂n

0 =∂p

∂b(46)

18

Notiamo che nei termini della pressione di arresto P

P = p+ %q2

2

e della vorticita le equazioni (46) possono anche essere scritte nella forma

∂P

∂s= 0

∂P

∂n= −%qωb

∂P

∂b= %qωn (47)

4.3 Equazioni di bilancio in coordinate ortogonali

A parte la forma vettoriale e quella intrinseca, scritture che permettono piudi leggere le equazioni di bilancio che di risolverle, notiamo ancora una voltache lo studio delle equazioni di bilancio e stato fatto finora in coordinatecartesiane, cioe in un sistema di riferimento nel quale la posizione di unpunto e identificata attraverso la intersezione di tre superfici di riferimentocostituite da piani ortogonali tra loro. In molti casi e opportuno adottareriferimenti in cui le superfici coordinate sono superfici diverse da quelle piane,per esempio cilindri o sfere, al fine di mettere in luce particolari simmetrie delmoto o di fare in modo che il corpo investito dalla corrente sia una superficiedi riferimento. Altre volte puo essere opportuno adottare riferimenti mobili,per esempio riferimenti rotanti solidalmente con il corpo in esame, e in questocaso nelle equazioni di bilancio si avranno forze apparenti dovute al fatto cheil nuovo riferimento non e piu inerziale. Per quel che riguarda il cambiamentodi coordinate in un riferimento inerziale consideriamo innanzitutto il sistemaCartesiano di coordinate x1, x2, x3 ed il nuovo sistema ξ1, ξ2, ξ3 di coordinatedefinito attraverso le equazioni

x1 = x1(ξ1, ξ2, ξ3) x2 = x2(ξ1, ξ2, ξ3) x3 = x3(ξ1, ξ2, ξ3)

In coordinate cartesiane la distanza di un generico punto P dall’origine O edata dall’espressione

P −O = x1i1 + x2i2 + x3i3

e l’elemento differenziale di lunghezza

dP = dx1i1 + dx2i2 + dx3i3

diventa nel nuovo sistema

dP = dξ1h1a1 + dξ2h2a2 + dξ3h3a3

19

dove i nuovi versori a1,a2,a3 e i coefficienti h1, h2, h3 della nuova metricasono dati da

a1 =1

h1

∂P

∂ξ1=

i1h1

∂x1∂ξ1

+i2h1

∂x2∂ξ1

+i3h1

∂x3∂ξ1

a2 =1

h2

∂P

∂ξ2=

i1h2

∂x1∂ξ2

+i2h2

∂x2∂ξ2

+i3h2

∂x3∂ξ2

a3 =1

h3

∂P

∂ξ3=

i1h3

∂x1∂ξ3

+i2h3

∂x2∂ξ3

+i3h3

∂x3∂ξ3

h21 =∂P

∂ξ1· ∂P∂ξ1

h22 =∂P

∂ξ2· ∂P∂ξ2

h23 =∂P

∂ξ3· ∂P∂ξ3

(48)

Notiamo che i nuovi versori di riferimento a1,a2,a3 sono tangenti alle nuovelinee coordinate, intersezione a due a due delle nuove superfici di riferimentoξ1 = costante, ξ2 = costante, ξ3 = costante. Se la trasformazione di coordi-nate considerata e ortogonale, allora questi versori sono anche normali allesuperfici di riferimento, e questo e il caso che considereremo in quel chesegue. Le condizioni di ortogonalita della trasformazione considerata sonoespresse dalle condizioni

a1 · a2 =1

h1

∂P

∂ξ1· 1

h2

∂P

∂ξ2=

1

h1h2

(∂x1∂ξ1

∂x1∂ξ2

+∂x2∂ξ1

∂x2∂ξ2

+∂x3∂ξ1

∂x3∂ξ2

)= 0

a2 · a3 =1

h2

∂P

∂ξ2· 1

h3

∂P

∂ξ3=

1

h2h3

(∂x1∂ξ2

∂x1∂ξ3

+∂x2∂ξ2

∂x2∂ξ3

+∂x3∂ξ2

∂x3∂ξ3

)= 0

a3 · a1 =1

h3

∂P

∂ξ3· 1

h1

∂P

∂ξ1=

1

h3h1

(∂x1∂ξ3

∂x1∂ξ1

+∂x2∂ξ3

∂x2∂ξ1

+∂x3∂ξ3

∂x3∂ξ1

)= 0

ed evidentemente si ha

a1 · a1 = a2 · a2 = a3 · a3 = 1

La distanza ds tra due punti puo ancora essere espressa in una forma pseudopitagorica data da

ds2 = dP · dP = δs21 + δs22 + δs23

dove gli elementi di lunghezza sulle nuove linee coordinate sono dati da

δs1 = h1dξ1 δs2 = h2dξ2 δs3 = h3dξ3

Notiamo che il simbolo δ esprime il fatto che i relativi incrementi di lunghez-za non sono differenziali esatti. Nei termini delle nuove coordinate ortogonaliξ1, ξ2, ξ3 il ds2, cioe la nuova metrica, e infatti data dall’espressione

ds2 = dP · dP = h21dξ21 + h22dξ

22 + h23dξ

23

Le componenti di un generico vettore u proiettato sia sulle vecchie che sullenuove coordinate saranno quindi espresse dalle componenti

u = U1i1 + U2i2 + U3i3 = u1a1 + u2a2 + u3a3

20

e le formule di trasformazione dalle vecchie alle nuove componenti sono dateda

u1 = u · a1 =U1

h1

∂x1∂ξ1

+U2

h1

∂x2∂ξ1

+U3

h1

∂x3∂ξ1

u2 = u · a2 =U1

h2

∂x1∂ξ2

+U2

h2

∂x2∂ξ2

+U3

h2

∂x3∂ξ2

u3 = u · a3 =U1

h3

∂x1∂ξ3

+U2

h3

∂x2∂ξ3

+U3

h3

∂x3∂ξ3

(49)

Fondamentali per quel che riguarda la scrittura delle equazioni di bilancionel nuovo sistema di coordinate ortogonali sono le espressioni del gradientedi uno scalare, del rotore e della divergenza di un vettore, della divergenzadi un tensore simmetrico. Il gradiente di uno scalare f e dato in coordinatecurvilinee da

∇f =a1

h1

∂f

∂ξ1+

a2

h2

∂f

∂ξ2+

a3

h3

∂f

∂ξ3(50)

il rotore di un vettore u da

(∇× u)1 = ω1 =1

h2h3

(∂u3h3∂ξ2

− ∂u2h2∂ξ3

)(∇× u)2 = ω2 =

1

h3h1

(∂u1h1∂ξ3

− ∂u3h3∂ξ1

)(∇× u)3 = ω3 =

1

h1h2

(∂u2h2∂ξ1

− ∂u1h1∂ξ2

)(51)

mentre la divergenza e data dall’espressione

∇ · u =1

h1h2h3

(∂(u1h2h3)

∂ξ1+∂(u2h3h1)

∂ξ2+∂(u3h1h2)

∂ξ3

)(52)

La divergenza di un tensore simmetrico πij ha in coordinate curvilinee orto-gonali una espressione piu complessa. Ricordiamo che mentre la divergenzadi un vettore e uno scalare, la divergenza di un tensore e un vettore. Si ha

(∇πij)1 =1

h1h2h3

(∂(π11h2h3)

∂ξ1+∂(π12h3h1)

∂ξ2+∂(π13h1h2)

∂ξ3

)+

+π21h1h2

∂h1∂ξ2− π22h1h2

∂h2∂ξ1

+π31h1h3

∂h1∂ξ3− π33h1h3

∂h3∂ξ1

(∇πij)2 =1

h1h2h3

(∂(π21h2h3)

∂ξ1+∂(π22h3h1)

∂ξ2+∂(π23h1h2)

∂ξ3

)+

+π32h2h3

∂h2∂ξ3− π33h2h3

∂h3∂ξ2

+π12h2h1

∂h2∂ξ1− π11h2h1

∂h1∂ξ2

(∇πij)3 =1

h1h2h3

(∂(π31h2h3)

∂ξ1+∂(π32h3h1)

∂ξ2+∂(π33h1h2)

∂ξ3

)+

+π13h3h1

∂h3∂ξ1− π11h3h1

∂h1∂ξ3

+π23h3h2

∂h3∂ξ2− π22h3h2

∂h2∂ξ3

(53)

21

In conclusione le equazioni di Navier-Stokes per flussi incompressibili

∇ · u = 0∂u

∂t+∇ · (πij) = −∇p

%πij = uiuj − τij (54)

si scrivono in coordinate ortogonali nelle seguente forma

∂(u1h2h3)

∂ξ1+∂(u2h3h1)

∂ξ2+∂(u3h1h2)

∂ξ3= 0

∂(u1h1h2h3)

∂t+∂(π11h2h3)

∂ξ1+∂(π12h3h1)

∂ξ2+∂(π13h1h2)

∂ξ3+

+π21h3∂h1∂ξ2− π22h3

∂h2∂ξ1

+ π31h2∂h1∂ξ3− π33h2

∂h3∂ξ1

= −h2h3%

∂p

∂ξ1

∂(u2h1h2h3)

∂t+∂(π21h2h3)

∂ξ1+∂(π22h3h1)

∂ξ2+∂(π23h1h2)

∂ξ3+

+π32h1∂h2∂ξ3− π33h1

∂h3∂ξ2

+ π12h3∂h2∂ξ1− π11h3

∂h1∂ξ2

= −h3h1%

∂p

∂ξ2

∂(u3h1h2h3)

∂t+∂(π31h2h3)

∂ξ1+∂(π32h3h1)

∂ξ2+∂(π33h1h2)

∂ξ3+

+π13h2∂h3∂ξ1− π11h2

∂h1∂ξ3

+ π23h1∂h3∂ξ2− π22h1

∂h2∂ξ3

= −h1h2%

∂p

∂ξ3(55)

dove

π11 = u1u1 − τ11 π22 = u2u2 − τ22 π33 = u3u3 − τ33π12 = u1u2 − τ12 π23 = u2u3 − τ23 π31 = u3u1 − τ31

e dove gli sforzi viscosi sono dati da

τ11 = 2ν

(1

h1

∂u1∂ξ1

+u2h1h2

∂h1∂ξ2

+u3h3h1

∂h1∂ξ3

)τ22 = 2ν

(1

h2

∂u2∂ξ2

+u3h2h3

∂h2∂ξ3

+u1h1h2

∂h2∂ξ1

)τ33 = 2ν

(1

h3

∂u3∂ξ3

+u1h3h1

∂h3∂ξ1

+u2h2h3

∂h3∂ξ2

)τ12 = ν

(h2h1

∂

∂ξ1

(u2h2

)+h1h2

∂

∂ξ2

(u1h1

))τ23 = ν

(h3h2

∂

∂ξ2

(u3h3

)+h2h3

∂

∂ξ3

(u2h2

))τ31 = ν

(h1h3

∂

∂ξ3

(u1h1

)+h3h1

∂

∂ξ1

(u3h3

))(56)

22

4.4 Equazioni di bilancio in coordinate cartesiane

La scrittura conservativa delle equazioni di bilancio per flussi incompressibilie data in coordinate cartesiane dalle espressioni

∂ux∂x

+∂uy∂y

+∂uz∂z

= 0 (57)

∂ux∂t

+∂uxux∂x

+∂uxuy∂y

+∂uxuz∂z

= −1

%

∂p

∂x+fx%

∂uy∂t

+∂uyux∂x

+∂uyuy∂y

+∂uyuz∂z

= −1

%

∂p

∂y+fy%

∂uz∂t

+∂uzux∂x

+∂uzuy∂y

+∂uzuz∂z

= −1

%

∂p

∂z+fz%

(58)

fx =∂τxx∂x

+∂τxy∂y

+∂τxz∂z

fy =∂τyx∂x

+∂τyy∂y

+∂τyz∂z

fz =∂τzx∂x

+∂τzy∂y

+∂τzz∂z

(59)

τxx = 2µ∂ux∂x

τyy = 2µ∂uy∂y

τzz = 2µ∂uz∂z

τxy = µ

(∂ux∂y

+∂uy∂x

)τyz = µ

(∂uy∂z

+∂uz∂y

)τzx = µ

(∂uz∂x

+∂ux∂z

)(60)

La vorticita ha come componenti in coordinate cartesiane

ωx =∂uz∂y− ∂uy

∂z

ωy =∂ux∂z− ∂uz

∂x

ωz =∂uy∂x− ∂ux

∂y(61)

23

La scrittura Lagrangiana delle equazioni di bilancio della quantita dimoto, sempre per flussi incompressibili, e infine data da

∂ux∂t

+ ux∂ux∂x

+ uy∂ux∂y

+ uz∂ux∂z

= −1

%

∂p

∂x+fx%

∂uy∂t

+ ux∂uy∂x

+ uy∂uy∂y

+ uz∂uy∂z

= −1

%

∂p

∂y+fy%

∂uz∂t

+ ux∂uz∂x

+ uy∂uz∂y

+ uz∂uz∂z

= −1

%

∂p

∂z+fz%

(62)

4.5 Equazioni di bilancio in coordinate cilindriche

Dopo il sistema cartesiano il sistema di coordinate ortogonali piu utile nelleapplicazioni e quello cilindrico. In esso le nuove superfici coordinate sono deipiani, z = costante, dei cilindri, r = costante, e dei semipiani, ϑ = costante.In questo caso abbiamo

x = r cosϑ y = r sinϑ z = z (63)

ar = ax cosϑ+ ay sinϑ

aϑ = −ax sinϑ+ ay cosϑ

az = az (64)

hr = 1 hϑ = r hz = 1 (65)

In base alle espressioni precedenti le equazioni di bilancio per flussi in-compressibili in coordinate cilindriche e in forma conservativa sono datedalle espressioni

∂(urr)

∂r+∂(uϑ)

∂ϑ+∂(uzr)

∂z= 0 (66)

∂(urr)

∂t+

∂(πrrr)

∂r+∂(πrϑ)

∂ϑ+∂(πrzr)

∂z− πϑϑ = −r

%

∂p

∂r

∂(uϑr)

∂t+

∂(πϑrr)

∂r+∂(πϑϑ)

∂ϑ+∂(πϑzr)

∂z+ πrϑ = −1

%

∂p

∂ϑ

∂(uzr)

∂t+

∂(πzrr)

∂r+∂(πzϑ)

∂ϑ+∂(πzzr)

∂z= −r

%

∂p

∂z(67)

πrr = urur − τrr πϑϑ = uϑuϑ − τϑϑ πzz = uzuz − τzzπrϑ = uruϑ − τrϑ πrz = uruz − τrz πϑz = uϑuz − τϑz (68)

24

τrr = 2µ∂ur∂r

τϑϑ = 2µ

(1

r

∂uϑ∂ϑ

+urr

)τzz = 2µ

∂uz∂z

τrϑ = µ

(∂uϑ∂r− uϑ

r+

1

r

∂ur∂ϑ

)τϑz = µ

(1

r

∂uz∂ϑ

+∂uϑ∂z

)τzr = µ

(∂ur∂z

+∂uz∂r

)(69)

La vorticita ha come componenti in coordinate cilindriche

ωr =∂uzr∂ϑ− ∂uϑ

∂z

ωϑ =∂ur∂z− ∂uz

∂r

ωz =∂uϑ∂r− ∂urr∂ϑ

+uϑr

(70)

Una forma di scrittura utile nelle applicazioni e la seguente

∂ur∂r

+∂uϑr∂ϑ

+∂uz∂z

+urr

= 0 (71)

∂ur∂t

+∂urur∂r

+∂uruϑr∂ϑ

+∂uruz∂z

+urur − uϑuϑ

r= −1

%

∂p

∂r+fr%

∂uϑ∂t

+∂uϑur∂r

+∂uϑuϑr∂ϑ

+∂uϑuz∂z

+2uruϑr

= − 1

r%

∂p

∂ϑ+fϑ%

∂uz∂t

+∂uzur∂r

+∂uzuϑr∂ϑ

+∂uzuz∂z

+uzurr

= −1

%

∂p

∂z+fz%

(72)

fr =∂τrr∂r

+∂τrϑr∂ϑ

+∂τrz∂z

+τrr − τϑϑ

r

fϑ =∂τϑr∂r

+∂τϑϑr∂ϑ

+∂τϑz∂z

+2τϑrr

fz =∂τzr∂r

+∂τzϑr∂ϑ

+∂τzz∂z

+τzrr

(73)

25

La scrittura Lagrangiana delle equazioni di bilancio della quantita dimoto in coordinate cilindriche e infine data dalle espressioni

∂ur∂t

+ ur∂ur∂r

+ uϑ∂urr∂ϑ

+ uz∂ur∂z− uϑuϑ

r= −1

%

∂p

∂r+fr%

∂uϑ∂t

+ ur∂uϑ∂r

+ uϑ∂uϑr∂ϑ

+ uz∂uϑ∂z

+uruϑr

= − 1

r%

∂p

∂ϑ+fϑ%

∂uz∂t

+ ur∂uz∂r

+ uϑ∂uzr∂ϑ

+ uz∂uz∂z

= −1

%

∂p

∂z+fz%

(74)

5 Flussi di punta

Vediamo ora di esaminare in dettaglio alcuni flussi semplici, rappresentativi,la cui soluzione matematica non presenta particolari difficolta. Notiamo chele soluzioni esatte delle equazioni di Navier Stokes sono poche per quel cheriguarda flussi stazionari e pochissime per quel che riguarda flussi variabilinel tempo. Per le soluzioni stazionarie occorre poi notare che esse fisica-mente sono verificate solo se il numero di Reynolds e sufficientemente basso,cioe possono diventare instabili per alti numeri di Reynolds, (un conto e lastazionarieta e un conto e la stabilita di una soluzione). Rimandiamo que-sto punto difficile e fondamentale al prossimo capitolo dove tratteremo leequazioni dei flussi turbolenti, e limitiamoci qui a ricavare formalmente que-ste soluzioni, cercando di discuterne per quanto possibile il reale significatofisico.

Notiamo innanzitutto che una semplice categoria di flussi e quella deipuri flussi di punta definiti come

u = u (x, t) v = w = 0 (75)

e duale dei puri flussi di taglio definiti come

u = u (y, t) v = w = 0 (76)

Il piu semplice flusso di punta e l’urto retto stazionario. Se trascuriamo glieffetti viscosi e termici abbiamo infatti dalle equazioni di bilancio

d(%u)

dx= 0

d(%uu+ p)

dx= 0

d

dx

(%uh+ %u

uu

2

)= 0 (77)

che ammettono la semplice soluzione

%1u1 = %2u2

26

%1u21 + p1 = %2u

22 + p2

h1 +u212

= h2 +u222

(78)

Queste equazioni, accoppiate all’equazione che lega l’entalpia a pressione edensita, forniscono il legame tra condizioni a monte e a valle dell’urto retto.Per gas perfetti l’entalpia e data da

h =γ

γ − 1

p

%

e si ottiene

(M2

M1

)2

=

1

M21

+γ − 1

2

γM21 −

γ − 1

2

%2%1

=u1u2

=(γ + 1)M2

1

(γ − 1)M21 + 2

p2p1

= 1 +2γ

γ + 1(M2

1 − 1)

T2T1

= 1 +2(γ − 1)

(γ + 1)2· γM

21 + 1

M21

(M21 − 1) (79)

Ricordiamo che il numero di Mach a monte e maggiore di uno, M1 > 1,quello a valle minore di uno, M2 < 1. Per onde d’urto molto deboli si haM1 'M2 ' 1. Per urti ipersonici, M1 →∞ abbiamo

%2%1

=u1u2→ γ + 1

γ − 1

p2p1→ 2γ

γ + 1M2

1

T2T1

→ 2γ(γ − 1)

(γ + 1)2M2

1 (80)

Ricordiamo anche che attraverso un urto la pressione di arresto diminuiscee l’entropia aumenta. Per urti deboli l’aumento di entropia e tuttavia cosıpiccolo che spesso si puo considerarlo isentropico.

Vediamo ora di valutare lo spessore di un urto retto. Chi determina ilsuo spessore e la viscosita, ma sia in questo caso che nel caso di un flusso ditaglio il ruolo della viscosita e semplicemente quello di diffondere il salto diquantita di moto e non certo di cambiarne il valore. Cosı come nei flussi ditaglio la vorticita generata dal moto impulsivo viene diffusa dalla viscositache addolcisce l’iniziale discontinuita di taglio formando lo strato limite, allostesso modo nell’urto la viscosita tende ad addolcire la discontinuita di punta

27

spalmandola su uno spessore finito. In uno strato limite laminare abbiamovisto che lo spessore δ e sostanzialmente dato da

δ

L' 1√

ReL

ed e quindi spontaneo chiedersi quale sia lo spessore di un urto. A questoscopo riscriviamo le prime due equazioni di bilancio tenendo ora conto deglieffetti viscosi

d(%u)

dx= 0

d

dx

(%uu+ p− µdu

dx

)= 0 (81)

Nel caso di urto debole possiamo supporre che l’urto sia isentropico e scrivereche

dp

dx=γp

%

d%

dx= a2

d%

dx= −%a

2

u

du

dx(82)

con a velocita del suono. Moltiplicando la seconda delle (81) per u eutilizzando la (82) si ottiene

%(u2 − a2)dudx

= ud

dx

(µdu

dx

)(83)

Per urti deboli abbiamo sostanzialmente

u1 = a+ ε u2 = a− ε

per cui possiamo scrivere

u2 − a2 = (u− a)(u+ a) ' 2u(u− a) ' u∆u

con ∆u = u1 − u2. Siamo ora in grado di valutare l’ordine di grandezza deivari termini nella (83). Otteniamo

%u∆u∆u

δu' uµ∆u

δ2u

dove δu e appunto lo spessore dell’urto da valutare e in conclusione si ricava

%δu∆u

µ' 1 (84)

il che vuol dire che il numero di Reynolds dello spessore dell’urto e dell’ordinedell’unita. Cio significa che per densita non troppo basse l’urto e una verae propria discontinuita.

Le relazioni dell’urto retto ci permettono anche di valutare l’effetto diuna forte esplosione in una atmosfera omogenea. A parte l’interesse proprio

28

del problema, esso viene qui trattato quale esempio di analisi dimensiona-le. Le grandezze significative del problema sono infatti l’energia E liberataistantaneamente dall’esplosione, la densita %0 e la pressione p0 dell’ambientein cui l’esplosione avviene. Cio che vogliamo determinare sono la velocitaU con cui si propaga l’urto sferico generato dall’esplosione e il raggio r daessa raggiunto al tempo t. Noti questi valori si possono stimare le pressioni,le densita e le temperature indotte dall’esplosione sulla base delle relazio-ni dell’urto ipersonico (80). Per esplosioni molto forti la contropressionep0 esercitata dall’ambiente sulla propagazione dell’urto diventa trascurabi-le, per cui possiamo dire che r dipende unicamente dall’energia E, dalladensita %0 e naturalmente dal tempo t. Se scriviamo la relazione monomiale

r ' %α0Eβtγ

otteniamo dimensionalmente

r '(E

%0

) 15

t25 (85)

ed essendo la velocita di propagazione U dell’urto data da

U =dr

dt

possiamo ricavare

U ' 2

5

(E

%0

) 15

t−35 ' 2

5

(E

%0

) 12

r−32 (86)

Attraverso le relazioni dell’urto retto ipersonico possiamo ora stimare lavelocita u, la densita % e la pressione p indotte dall’esplosione. Sulla basedelle (80) possiamo scrivere

%

%0=

U

U − u→ γ + 1

γ − 1

p

p0→ 2γ

γ + 1M2

0 =2

γ + 1

%0U2

p0

da cui si ottiene

u → U2

γ + 1

p → 2

γ + 1%0U

2 (87)

Nel caso di esplosioni atomiche l’unita di misura piu appropriata e ilKilotone, cioe l’energia sviluppata dall’esplosione di mille tonnellate di tri-nitrotoluolo (tritolo). L’energia sviluppata da un chilogrammo di tritolo e di

29

circa 4500kJ/kg. Sulla base di questi dati si puo stimare l’energia sviluppa-ta dall’esplosione di figura (15). Le considerazioni svolte in questi paragrafosono sostanzialmente quelle esposte nei lavori di L. I. Sedov , Le mouve-ment d’air en cas d’une forte explosion e di G. I. Taylor, The formation of ablast wave by a very intense explosion, pubblicate rispettivamente nel 1946sui Comptes Rendues dell’Accademia delle Scienze Sovietica, vol. 52, pagg.17-20, e nel 1950 sui Proceedings della Royal Society di Londra, serie A,vol. 201, pagg. 175-186. Per quel che riguarda ulteriori approfondimenti sianel campo dei metodi dimensionali d’indagine che in quello della fisica delleforti onde d’urto segnaliamo i volumi di L. I. Sedov e di Ya. B. Zeldovich eYu. B. Raizer riportati in bibliografia.

6 Flussi di taglio piani

Occupiamoci ora dei puri flussi di taglio, cioe quei flussi per cui

u = u (y, t) v = w = 0 (88)

Notiamo che i flussi di taglio sono rotazionali, le componenti della vorticitasono date da

ωx = ωy = 0 ωz = −∂u∂y

(89)

e se ci limitiamo a considerare flussi incompressibili possiamo scrivere

%∂u

∂t= −∂p

∂x+ fx

0 = −∂p∂y

fx =∂τxy∂y

τxy = µ∂u

∂y= −µωz (90)

Queste equazioni che governano i flussi di taglio sono molto simili aquelle dello strato limite nelle quali sostanzialmente la derivata temporale esostituita da una derivata convettiva. Notiamo che per i flussi di taglio p ecostante nella direzione y, cioe in direzione normale alle traiettorie che sonoin questo caso ovviamente le rette y = costante. Essendo inoltre u = u (y, t)si ricava subito che p deve essere data da

p = −Gx

con G costante. La soluzione stazionaria delle (90) e evidentemente data da

u = a+ by − G

2µy2

30

con a e b costanti d’integrazione che permettono di fissare i valori di u sudue piani paralleli. Due casi sono particolarmente interessanti. Il primo e ilflusso alla Couette in un meato di altezza L e con una pareta fissa ed unamobile a velocita uL. In assenza di gradiente di pressione, G = 0, abbiamo

u = uLy

L

Il secondo e relativo al flusso in un canale di altezza 2L, e si ottiene

u

u0= 1−

(y

L

)2

G =2µu0L2

con u0 velocita al centro. Notiamo che la velocita sull’asse u0 e anche lavelocita massima, mentre la velocita media um definita come rapporto traportata in volume Q e sezione del canale e data da

um =Q

2L=

1

2L

∫ L

−Ludy =

2u03

Per il flusso nel canale il numero di Reynolds e generalmente definito neitermini della velocita media e della larghezza 2L

Re2L =um2L

ν(91)

e ricordiamo che per Re2L maggiore di 1400 il flusso diventa instabile.Vediamo ora come evolvono nel tempo alcuni flussi di taglio nel caso piu

semplice in cui p e costante dappertutto, il che porta alla semplice equazione

∂u

∂t= ν

∂2u

∂y2(92)

dove ν = µ/% e la viscosita cinematica. Consideriamo innanzitutto un flussodi taglio che inizialmente e dato dall’espressione, vedi figura (16)

u (y, 0) = U0 cos

(2πy

L

)In questo caso la (92) puo essere risolta per separazione di variabili. Seponiamo infatti

u (y, t) = U (t) cos

(2πy

L

)otteniamo

dU

dt+ νU

(2π

L

)2

= 0

che risolta da

U (t) = U0 exp

(− t

tvisc

)

31

dove il tempo caratteristico di decadimento della ampiezza iniziale U0 pereffetto viscoso e dato da

tvisc =L2

4π2ν(93)

Notiamo che il tempo di decadimento e tanto piu piccolo quanto piu ladimensione L dello strato vorticoso iniziale e piccola, e quanto piu la visco-sita cinematica e grande. Cio e di grande importanza nella dinamica dellavorticita e, come vedremo, della turbolenza. La dissipazione viscosa agiscesui piccoli vortici, mentre i grossi vortici decadono inerzialmente. Il risul-tato trovato e ovviamente corretto dal punto di vista fisico solo se tvisc edell’ordine o inferiore al tempo caratteristico inerziale del fenomeno

tinerz =L

U0(94)

Notiamo che il rapporto tra i due tempi e scalato come il numero caratteri-stico di Reynolds del flusso in esame

Re =%U0L

µ=U0L

ν= 4π2

tvisctinerz

(95)

e chiediamoci cosa avviene se questo numero e molto grande. In questo casoi tempi di decadimento della vorticita cosı calcolati sono molto piu grandidi quelli che si registrano nella realta, e in natura assistiamo invece alla co-siddetta cascata inerziale che consiste essenzialmente nella rapida nascita diinstabilita inerziali tra strato vorticoso e strato vorticoso, e nella formazionein cascata di vortici sempre piu piccoli sui quali l’effetto viscoso si fa sentirein maniera sempre piu efficace. Questo processo di cascata inerziale che eper sua stessa natura non stazionario, caotico e tridimensionale e essenzial-mente cio che va sotto il nome di turbolenza e la sua descrizione numericaimpone l’uso delle equazioni complete non stazionarie e tridimensionali. At-traverso le simulazioni numeriche si scopre allora che il flusso puro di taglioqui studiato diventa instabile ad alti numeri di Reynolds, con conseguentenascita di moti inerziali che attraverso appunto la cascata inerziale accele-rano molto il decadimento viscoso. Sottolineiamo tuttavia il fatto che lacascata inerziale non e dissipativa. La dissipazione avviene sempre a livellodei vortici piu piccoli e grazie alla viscosita. Torneremo su cio in maggiordettaglio quando parleremo dello strato limite turbolento.

Vediamo ora un secondo caso di flusso di taglio non stazionario, quelloche fisicamente corrisponde ad una accelerazione impulsiva di una lastra pia-na che viene istantaneamente messa in moto, vedi figura (17). Le condizioniiniziali e al contorno sono date da

u (y, 0) = 0 y > 0 u (0, t) = U0 t ≥ 0

32

dove ora U0 e la velocita della parete. Il moto si comunica per effetto dellaviscosita al fluido, e la soluzione della (92) puo in questo caso essere otte-nuta introducendo una opportuna variabile di similitudine che come vedre-mo ridurra l’equazione alle derivate parziali ad una equazione alle derivateordinarie. Se introduciamo infatti la variabile di similitudine η

η =y

2√νt

otteniamo

∂

∂t= − y

4t√νt

∂

∂η

∂

∂y=

1

2√νt

∂

∂η

e l’equazione (92) si riduce alla

d2u

dη2+ 2η

du

dη= 0

che ha come soluzione

u = U0

(1− 2√

π

∫ η

0exp

(−z2

)dz

)(96)

Se definiamo una profondita di penetrazione δ tale che per essa si e raggiuntauna velocita u = 0.01U0, si ottiene un valore per la variabile di similitudineη di circa 2. Abbiamo cioe

δ0.01 ' 4√νt (97)

e sottolineiamo anche in questo caso il significato peculiare della viscositacinematica ν, che e quello di grandezza che controlla la diffusivita dellaquantita di moto nel tempo per effetto viscoso, mentre la viscosita µ e quellache controlla l’intensita dello sforzo di taglio τxy

τxy = µ

(∂u

∂y

)

7 Flussi di taglio cilindrici

Oltre ai flussi di taglio a simmetria piana sono particolarmente interessantiquelli a simmetria cilindrica. Mentre nel caso della simmetria piana avevamoa che fare con piani che scorrevano parallelamente a piani, ora si tratta dicilindri che scorrono dentro a cilindri. Notiamo subito che si possono averedue casi di scorrimento, quello in cui la direzione di scorrimento e assiale,flusso nei tubi, e quella in cui lo scorrimento e periferico, e i cilindri ruotanointorno ad un asse comune. Il sistema di riferimento piu appropriato per

33

lo studio di questi flussi di taglio e ovviamente quello cilindrico. Nel primocaso consideriamo i moti per cui

uz = uz(r, t) uϑ = ur = 0

In essi la vorticita ha come unica componente non nulla ωϑ

ωϑ = −∂uz∂r

e se ci limitiamo a considerare flussi incompressibili le equazioni di bilancioin coordinate cilindriche si riducono alle seguenti

0 =∂p

∂r

0 =∂p

∂ϑ

%∂uz∂t

= −∂p∂z

+ fz (98)

con

fz =1

r

∂rτzr∂r

=∂τzr∂r

+τzrr

τzr = µ∂uz∂r

= −µωϑ

Nel secondo caso consideriamo i moti per cui

uϑ = uϑ(r, t) ur = uz = 0∂p

∂ϑ= 0

In questo caso la vorticita e data da

ωz =∂uϑ∂r

+uϑr

(99)

e le equazioni si riducono alle seguenti

%uϑuϑr

=∂p

∂r

%∂uϑ∂t

= fϑ

0 =∂p

∂z(100)

con

fϑ =∂τrϑ∂r

+ 2τrϑr

=1

r2∂r2τrϑ∂r

τrϑ = µ

(∂uϑ∂r− uϑ

r

)= µr

∂

∂r

(uϑr

)

34

Notiamo che la vorticita ωz data dalla (99) e la somma di due termini. Ilprimo esprime come al solito la velocita angolare di rotazione su se stesso del-l’elemento fluido, mentre il secondo corrisponde ad una velocita di rotazionerigida di trascinamento dovuta al riferimento di coordinate adottato.

7.1 Flusso nei tubi

Consideriamo ora piu in dettaglio i moti cilindrici di taglio del primo tipo.Un caso tipico e quello relativo al flusso nei tubi. Si verifica infatti facilmenteche

uzu0

= 1−(r

a

)2

p = −Gz

e una soluzione stazionaria del sistema di equazioni (98) se

G =4µu0a2

Questo moto e anche detto moto di Hagen-Poiseuille. Notiamo che la velo-cita sull’asse u0 e anche la velocita massima, mentre la velocita media umdefinita come rapporto tra portata in volume Q e sezione del tubo e data da

um =Q

πa2=

1

πa2

∫ a

02πrudr =

u02

Anche per il flusso di Poiseuille il numero di Reynolds e generalmente definitonei termini della velocita media e del diametro D = 2a ed e uguale a quellodefinito nei termini della velocita massima e del raggio

ReD =umD

ν=u0a

ν(101)

e ricordiamo che per ReD maggiore di 2300 il flusso diventa instabile.

7.2 Vortice lineare

Consideriamo ora i moti del secondo tipo. Si puo facilmente verificare chenel caso di flussi stazionari una soluzione del sistema (100) e il vortice

uϑ =Γ

2πrp = p∞ −

%Γ2

8π2r2(102)

Notiamo alcune peculiarita di questo moto. Esso e irrotazionale, ωz = 0, equindi si conserva la pressione di arresto P

P = p+%uϑuϑ

2= p∞ (103)

Per quel che riguarda lo sforzo viscoso τrϑ esso non e nullo e vale

τrϑ = − µΓ

πr2(104)

35

mentre la forza viscosa e nulla. Notiamo che anche il campo di velocita

uϑ =Γ

2πr

(1− exp

(− r2

4νt

))(105)

e una soluzione non stazionaria del sistema (100). Anche in questo casovale il discorso fatto per il decadimento di flussi di taglio piani. I tempi didecadimento previsti dalla (105) per un vortice lineare sono estremamentelunghi. In realta un vortice si destabilizza attraverso deformazioni e contor-sioni inerziali che in certo senso lo frantumano in formazioni vorticose semprepiu piccole. Su queste ultime agisce efficacemente la viscosita diffondendolenello spazio e dissipandole.

7.3 Vortice di Rankine

Un’altra soluzione stazionaria relativa ai moti del secondo tipo e quella chedescrive il puro moto rotatorio. In questo caso abbiamo

uϑ = Ωr τrϑ = 0 ωz = 2Ω p = p0 +Ω2r2

2(106)

e notiamo che la pressione di arresto non si conserva, essendo il fluido rota-zionale. In pratica si incontrano spesso formazioni vorticose formate da uncuore rotatorio e da una periferia irrotazionale. Il campo di velocita di que-ste formazioni vorticose puo essere in prima approssimazione rappresentatoda

uϑ = Ωr r < r0

uϑ =Γ

2πrr > r0

Ovviamente per assicurare la continuita del campo di velocita occorre che

Ωr0 =Γ

2πr0

ed un campo di moto di questo tipo e detto vortice di Rankine. L’andamentodelle pressioni statiche in un vortice di Rankine puo essere determinato nellaparte irrotazionale esterna tramite il teorema di Bernoulli. Se indichiamocon p∞ la pressione all’infinito abbiamo per r > r0

p = p∞ −%Γ2

8π2r2

mentre per r < r0 occorre integrare l’equazione di bilancio della quantita dimoto che esprime l’equilibrio di forze centrifughe e forze di pressione

%uϑuϑr

=∂p

∂r

36

a partire da p0, pressione statica al centro del vortice. Si ottiene

p = p0 +%Ω2r2

2

e se raccordiamo questa espressione per la pressione con quella data dalbinomio di Bernoulli per r = r0 abbiamo che

p∞ − p0 = %Ω2r20 = %u2ϑ0 (107)

dove uϑ0 rappresenta la velocita massima.Notiamo infine che la soluzione stazionaria generale del sistema (100) e

data dall’espressione

uϑ = Ωr +Γ

2πr(108)

con Ω e Γ costanti arbitrarie. E’ possibile in questo modo determinarel’andamento del flusso alla Couette tra due cilindri coassiali di raggi r1 < r2rotanti a velocita diverse uϑ1, uϑ2. Si dimostra che questo flusso e stabile se

uϑ2r2 > uϑ1r1 (109)

7.4 Vortice lineare compressibile

Se trascuriamo gli effetti dovuti alla compressibilita del gas, la pressioneall’interno di un vortice la cui velocita periferica e data dall’espressione

uϑ =Γ

2πr

viene espressa dalla legge di Bernoulli

p = p∞ −%u2ϑ2

= p∞ −%Γ2

8π2r2

dove con p∞ si indica la pressione all’infinito, la dove la velocita del vorticee nulla. Naturalmente questa approssimazione e possibile se il numero diMach Mϑ e sufficientemente basso. Al fine di vedere l’effetto della compres-sibilita imponiamo che tra linea di corrente e linea di corrente non si conserviBernoulli, ma l’entalpia di arresto. Cio e ovviamente possibile se nell’equa-zione di bilancio di quest’ultima trascuriamo gli effetti viscosi e termici, epossiamo scrivere

h = h∞ −u2ϑ2

= h∞ −Γ2

8π2r2

dove h e l’entalpia per unita di massa ed h∞ il suo valore all’infinito. Essendoper i gas perfetti

h = cpT =γ

γ − 1

p

%=

c2

γ − 1

37

dove c e la velocita del suono

c =

√γp

%=

√γRT

M

si arriva alla relazione

Γ =2πrc∞√1

M2ϑ

+γ − 1

2

che lega il numero di Mach Mϑ al raggio r e dove c∞ rappresenta la velocitadel suono all’infinito. Questa relazione e del massimo interesse in quanto cidice che il raggio sonico rson, cioe quello per cui Mϑ = 1, si ha per

rson =Γ

2πc∞

√γ + 1

2

mentre il raggio limite, o minimo, rmin, quello per cui Mϑ diventa infinitosi ha per

rmin =Γ

2πc∞

√γ − 1

2

7.5 Vortice di Rankine compressibile

L’effetto della compressibilita nel caso di un vortice di Rankine e piu com-plesso. Abbiamo visto che nel caso incompressibile si ha

uϑ = Ωr r < r0

uϑ =Γ

2πrr > r0

dove per continuita

Ωr0 =Γ

2πr0

mentre il campo delle pressioni e dato da

p = p0 +%Ω2r2

2r < r0

p = p∞ −%Γ2

8π2r2r > r0

dove per continuita

p∞ − p0 = %Ω2r20

Se si vuole tenere conto della compressibilita, una ragionevole supposizio-ne e che nella zona irrotazionale, cioe per r > r0, si conservi ancora l’entalpia

38

d’arresto, mentre per r < r0 e piu plausibile fisicamente che si conservi tralinea di corrente e linea di corrente la temperatura statica T = T0. In sostan-za facciamo l’ipotesi che la zona irrotazionale sia adiabatica mentre quellarotazionale sia isoterma. Per quel che riguarda r > r0 non c’e nulla di nuovoda aggiungere mentre per quel che riguarda r < r0 dobbiamo ora integrarel’equazione del moto

%uϑuϑr

=∂p

∂r(110)

con la condizione che

p =%RT0M

(111)

Naturalmente anche in questo caso occorre raccordare le due soluzioni tro-vate per r = r0.

8 Flussi rotazionali inviscidi

Il vortice di Rankine ci introduce ad una classe di flussi di particolare im-portanza pratica e di notevole difficolta teorica : i flussi rotazionali inviscidi.Ricordiamo che se il numero di Knudsen e molto minore di uno il moto delfluido e dominato dagli urti tra le molecole e il flusso gassoso puo esseredescritto come un moto di mezzo continuo, se il numero di Mach e sufficien-temente piccolo rispetto all’unita il mezzo puo essere considerato a densitacostante e se il numero di Reynolds e sufficientemente elevato possono esseretrascurate le forze viscose. Trascurare le forze viscose non vuole dire tuttaviache il flusso sia irrotazionale. Casi di flussi essenzialmente non viscosi, cioein cui sono trascurabili le forze viscose rispetto a quelle d’inerzia, e rotazio-nali, non mancano, sia per quel che riguarda moti liberi di grosse formazionivorticose sia per quel che riguarda flussi esterni rotazionali che investonoun corpo. Ai primi appartengono il vortice di Rankine visto in precedenzacome esempio di moto di puro taglio, mentre ai secondi appartengono flussicome quello relativo ad un cilindro investito da una corrente di taglio datada

U = U0 + ky (112)

In questo caso il flusso esterno e rotazionale, la sua vorticita lungo l’assez e data da ωz = −k e la velocita attorno al corpo non e derivabile comegradiente di un potenziale. Notiamo che flussi esterni di questo tipo siproducono quando flussi di scia o flussi di strato limite o in genere flussiseparati vanno ad investire altri corpi. In questo caso si tratta di determinareil flusso non viscoso esterno su cui poi si calcolera lo strato limite a parete.Una causa ulteriore che marchia rotazionalmente un flusso imprimendoglivorticita e la presenza di onde d’urto curve, attraverso le quali si conserva

39

l’entalpia d’arresto H ma non l’entropia s, che cambia da linea di flussoa linea di flusso per via della diversa inclinazione dell’urto sulla correnteindisturbata. Si puo dimostrare che anche in questo caso si ha la nascitadi vorticita a valle dell’urto incurvato. Per quel che riguarda moti liberi digrosse formazioni vorticose citiamo ancora i vortici di estremita alari e leloro interazioni con i vortici di estremita dei flaps e dei piani di di coda, leschiere di vortici alternati che si formano nelle scie di corpi tozzi, le grossestrutture vorticose naturali quali i mulinelli, i tornado e gli uragani. La lorodimensione e notevole e a livello di questa scala, spesso detta macroscala delfenomeno, il relativo numero di Reynolds e generalmente elevato e i fenomeniviscosi possono essere trascurati. Di conseguenza i flussi vorticosi diventanoReynolds indipendenti, ma e chiaro tuttavia che i sottili strati limite che sisviluppano tra parete e fluido o tra fluido rotazionale di scia e fluido esternohanno scale notevolmente piu piccole, e che quindi al loro livello gli effettiviscosi non solo non possono essere trascurati ma sono l’agente essenziale disforzi e dissipazioni.

A livello della macroscala cio che piu importa e la dinamica della vor-ticita, e lo studio della vorticita e tra i piu importanti e complessi dellameccanica dei fluidi. In aerodinamica si considerano essenzialmente flussi avorticita fissa, aderente ai corpi attraverso strati limite attaccati e che nonpresentano separazione. La determinazione di questa vorticita aderente emolto semplice nel caso di flussi bidimensionali, ed e fatta imponendo laposizione del punto di arresto posteriore, condizione di Kutta. Molto spes-so il flusso presenta invece delle separazioni e dalle fauci dello strato limiteche si aprono sulla scia viene emessa vorticita. In corrispondenza a que-sta emissione si ha una variazione uguale e contraria della vorticita ad essoaderente, e questo fenomeno puo diventare non stazionario, dando luogo aduna emissione alternata di vortici che a loro volta determinano fluttuazionidi pressione e inducono vibrazioni sul corpo. E’ opportuno segnalare subi-to che lo studio della vorticita mostra che sotto certe condizioni essa evolveLagrangianamente, cioe seguendo le particelle materiali. Al fine di compren-dere cio e necessario fare alcuni richiami cinematici di cui ci occuperemo nelparagrafo seguente.

8.1 Materialita di punti, linee e superfici

Supponiamo dato un campo di moto definito in un riferimento Cartesianotramite le componenti di velocita

u = u(x, y, z, t) v = v(x, y, z, t) w = w(x, y, z, t) (113)

e chiediamoci se un generico punto, o una linea, o una superficie che simuove nello spazio e materiale, cioe se e sempre composta dalle stesse par-ticelle. Ovviamente essendo immersi in un campo di velocita cio avviene

40

se ad ogni istante la velocita in ogni punto e quella del campo di moto da-to. Consideriamo innanzitutto il moto di un punto definito attraverso leespressioni

x = x(t) y = y(t) z = z(t) (114)

Perche esso sia materiale occorre evidentemente che

dx

dt= u

dy

dt= v

dz

dt= w (115)

e solo se queste condizioni sono soddisfatte il moto del punto in esame emateriale nel campo di velocita dato. Il caso di una linea e leggermente piucomplesso. Consideriamo una linea mobile nel tempo descritta attraverso lerelazioni

x = x(λ, t) y = y(λ, t) z = z(λ, t) (116)

dove λ e una generica coordinata curvilinea. E’ chiaro allora che ad ogniistante t abbiamo una curva, e ci chiediamo se essa e sempre composta dallestesse particelle nel campo di moto dato, cioe se essa e materiale. Perchecio avvenga occorre che

∂2x

∂t∂λ=

∂2x

∂λ∂t=∂u

∂λ=

=∂u

∂x

∂x

∂λ+∂u

∂y

∂y

∂λ+∂u

∂z

∂z

∂λ

e se indichiamo con ϑ il campo di vettori tangenti alla curva in ogni istante

ϑ =dP

dλ(117)

cioe

ϑx =∂x

∂λϑy =

∂y

∂λϑz =

∂z

∂λ(118)

possiamo scrivere la condizione di materialita sotto la forma

Dϑ

Dt= ϑ · ∇u (119)

Vediamo ora le condizioni di materialita di una superficie mobile neltempo espressa nella forma

f(x, y, z, t) = 0 (120)

Anche in questo caso la superficie f e materiale se l’espressione

∂f

∂t+∂f

∂x

dx

dt+∂f

∂y

dy

dt+∂f

∂z

dz

dt(121)

41

e uguale a zero quando

dx

dt= u

dy

dt= v

dz

dt= w (122)

e quindi la relazione di materialita e data dall’annullarsi della derivataLagrangiana

∂f

∂t+ u · ∇f = 0 (123)

8.2 Equazione di Helmoltz. Dinamica della vorticita.

Notiamo ora la fondamentale e ovvia conseguenza del fatto che la vorticitae per definizione un rotore, e quindi che essa e solenoidale e costretta adorganizzarsi in tubi vorticosi che o si chiudono su se stessi o si chiudonoall’infinito. Abbiamo cioe

∇ · ω ≡(∂ωx∂x

+∂ωy∂y

+∂ωz∂z

)≡ 0

dove con i simboli ωx, ωy e ωz si indicano le tre componenti Cartesiane di ω ,e notiamo che il fatto matematico che la divergenza della vorticita e nullasignifica fisicamente che non ci sono ne pozzi ne sorgenti di vorticita sottonessuna condizione. L’evoluzione nel tempo della vorticita nei mezzi fluidi emesso bene in luce dalla cosiddetta equazione di Helmoltz ottenuta facendoil rotore della equazione che esprime il bilancio della quantita di moto

∂u

∂t+ ω × u = −∇p

%−∇

(u · u

2

)(124)

in assenza di forze viscose, cioe per alti numeri di Reynolds. Se il flusso ebarotropico, cioe sia nel caso in cui % = costante, (flussi incompressibili), sianel caso in cui ∇p/% = ∇h, (flussi isentropici), si ottiene

Dω

Dt= ω · ∇u− ω ∇ · u (125)

dove si e fatto uso della identita vettoriale

∇× (a× b) ≡ b · ∇a− b∇ · a− a · ∇b + a∇ · b (126)

e del fatto che ∇ · ω ≡ 0. L’equazione cosı ottenuta descrive la dinamicadella vorticita e puo essere espressa in forma piu leggibile sfruttando larelazione che esprime il bilancio della massa

D%

Dt+ %∇ · u = 0

attraverso la quale si puo scrivere

D

Dt

(ω

%

)=

(ω

%

)· ∇u (127)

42

dove D/Dt esprime al solito la derivata Lagrangiana

D

Dt=

∂

∂t+ u · ∇

Il termine a sinistra dell’equazione scritta ha evidentemente il significato ditrasporto convettivo della vorticita, mentre il termine a destra esprime ilcosiddetto stretching, stiramento, delle linee vorticose dovuto al gradientedella velocita. Notiamo che sulla base di quanto detto nel paragrafo prece-dente questa equazione si legge come una conservazione materiale delle lineevorticose P (λ, t) che ammettono come campo di vettori tangenti

dP

dλ=ω

%

Se quindi con dP indichiamo la lunghezza di un elementino delle stesseall’istante t e con dP0 il valore dello stesso elementino ad un istante t0allora abbiamo

dλ =| dP || ω |%

=| dP0 || ω 0 |%0

e quindi

| dP || dP0 |

=

| ω |%

| ω 0 |%0

(128)

Notiamo ora che se indichiamo con dA la sezione di un tubicino vorticoso altempo t e con dA0 la sua sezione al tempo t0, la conservazione della vorticitacontenuta nel tubicino vorticoso considerato impone che

| ω | dA =| ω 0 | dA0 (129)

mentre la conservazione della massa si puo semplicemente scrivere come

% | dP | dA = %0 | dP0 | dA0

dalle quali si ottiene sempre la relazione (128)

% | dP || ω 0 |= %0 | dP0 || ω |

9 Flussi di strato limite.

Nello spirito di questo corso vediamo ora alcune soluzioni semplici, rappre-sentative, dei flussi di strato limite, cioe di quei flussi che si insinuano trala corrente esterna e la parete e ne raccordano le velocita. Notiamo innan-zitutto che lo strato limite stazionario e sostanzialmente un flusso di taglio

43

nel quale alla derivata temporale si sostituisce una derivata convettiva, e ilflusso evolve non nel tempo ma lungo il corpo a partire dal punto di attacco.Naturalmente c’e una notevole analogia tra le due evoluzioni: un nuovo mo-do di stimare lo spessore dello strato limite laminare e in particolare quellodi applicare ad esso il risultato relativo alla profondita di penetrazione dellavelocita in un fluido messo in moto dallo scorrimento impulsivo di un pia-no. Il tempo convettivo e nello strato limite dato da t = x/Ue dove x e ladistanza dal punto di arresto e Ue la velocita del flusso esterno. Abbiamoallora dalla (97)

δ

x' 1√

Rex

dove

Rex =Uex

ν

e che conferma la relazione trovata in precedenza. Senza entrare nei detta-gli delle varie particolarita dello strato limite incompressibile, compressibile,bidimensionale, tridimensionale, con o senza gradienti di pressione, lamina-re o turbolento, stazionario o non stazionario, riassumiamo alcuni aspettiessenziali. Un primo punto e che lo strato limite e generalmente molto sot-tile rispetto alle dimensioni del corpo che avvolge. Abbiamo visto che ilsuo spessore δ e scalato nel laminare rispetto alla dimensione caratteristicaL del corpo come 1/

√ReL. Cio permette la sua trattazione, anche su cor-

pi complessi e a forte curvatura superficiale, in una geometria semplificata,nella quale x e z sono due coordinate curvilinee superficiali generalmenteortogonali tra loro e con origine nel punto di arresto del flusso esterno, edy una coordinata ad essa normale. Un secondo punto importante e che latrattazione dello strato limite e generalmente subordinata alla conoscenzadi un flusso esterno calcolato sulla base delle equazioni di Eulero e al qualela soluzione di strato limite si sovrappone. In un prossimo futuro, sia conlo sviluppo dei calcolatori sia con lo sviluppo di algoritmi di calcolo semprepiu potenti si potra pensare a soluzioni complete delle equazioni di Navier-Stokes, ma al momento e in particolare per numeri di Reynolds abbastanzaelevati non ci sono valide alternative a questa metodologia. Metodologiache del resto sara sempre valida per spiegare la fenomenologia dello stra-to limite e che inoltre puo essere iterativamente applicata per ricalcolare ilflusso non viscoso esterno sulla base del calcolo di strato limite e tenendoconto delle sue previsioni, (spostamento verso l’esterno del flusso potenziale,determinazione di eventuali separazioni che impongono nuove e diverse con-dizioni di Kutta sul corpo). Un terzo punto e che nello strato limite non c’erecupero di pressione, e la pressione e praticamente quella del flusso ester-no. Come abbiamo visto questa e la grande differenza tra flussi di taglio eflussi irrotazionali: nei flussi di taglio il teorema di Bernoulli non vale piu e

44

praticamente la pressione resta inalterata in direzione normale alle linee dicorrente, cioe normalmente alla parete nei flussi di strato limite. Notiamoche questa invarianza della pressione nella direzione normale alla parete epraticamente cio che permette una trattazione di strato limite cosı comedescritta, e notiamo anche che le accelerazioni e le decelerazioni del flussoesterno sono molto amplificate nello strato limite e tanto piu quanto piu sie prossimi a parete. Per rendersene conto teniamo presente che il teoremadi Bernoulli applicato al flusso esterno dice che una variazione dpe/dx dellapressione causa in esso una variazione di velocita pari a

%UedUedx

= −dpedx

(130)

Una scorretta, ma non troppo, applicazione del teorema di Bernoulli nellostrato limite nella direzione della corrente, cioe in direzione x, permette discrivere

%udu

dx≈ −dp

dx(131)

ed inoltre si ha

dp

dx=dpedx

(132)

in quanto la pressione non cambia normalmente alla parete. Si puo quindistimare che

UedUedx≈ udu

dx(133)

Abbiamo allora lungo una linea di corrente interna allo strato limite

du

u≈ U2

e

u2dUeUe

(134)

da cui si vede che una variazione percentuale nella corrente esterna si am-plifica per esempio di 100 volte la dove u/Ue = 0.1. Cio puo rapidamenteportare in presenza anche di deboli decelerazioni del flusso esterno alla in-versione di velocita nello strato limite e quindi alla separazione del flusso aparete, vedi figura (18), dove si avrebbe non solo u = 0 ma anche(

∂u

∂y

)p

= 0 (135)

e quindi sforzo nullo. La separazione puo avvenire nello strato limite lami-nare, oppure lo strato limite laminare puo diventare sede di instabilita chelo trasformano in turbolento, non riuscendo egli piu a reggere lo sforzo dicoordinare in maniera coerente tutto il flusso di taglio che si e accumulatoa partire dal punto di arresto tra la parete e il flusso esterno. Dal punto divista della resistenza di attrito cio e uno svantaggio perche come vedremo

45

essa aumenta, ma dal punto di vista della separazione cio e un vantaggio inquanto la agitazione turbolenta rivitalizza lo strato limite trasferendo quan-tita di moto dal flusso esterno allo strato limite molto piu rapidamente diquanto operato dalla sola agitazione termica, e cioe dai soli sforzi viscosi.Cio e messo bene in luce dal comportamento dello strato limite attorno ad uncilindro, vedi figura (19), dove si nota al progressivo aumentare del numerodi Reynolds il verificarsi della separazione laminare, del passaggio alla tur-bolenza, della separazione turbolenta, molto piu ritardata e tale da produrreun scia piu stretta e un flusso piu avvolgente. E’ opportuno a questo puntosottolineare che dal punto di vista della configurazione aerodinamica di uncorpo e della massima importanza ottenere flussi attaccati ed evitare quindiseparazioni. Tra i tanti possibili esempi che suffragano questa affermazionene citiamo uno tratto dal rapporto NASA CP 2283, Parte II, Autori vari:Shuttle Performance: Lessons Learned, relativo alla aerodinamica del vetto-re dello Shuttle durante il suo trasferimento dalla base di Edwards a quelladi Cap Canaveral, operato con un Boeing 747, vedi figure (20-23). I proble-mi aerodinamici affrontati erano evidentemente molto grossi e abbastanzainusuali. Nell’appendice B del testo citato viene esaminata anche sotto que-sto aspetto la lezione imparata dall’esperienza dello Shuttle, e l’autore, A.H. Eldridge della Boeing, dice testualmente:

Among the lessons learned from (or perhaps really reaffirmed by) thissatisfying program have been:

• We must always design to achieve orderly airflows (usually attached)and benign vortex shedding from all external surfaces.

• . . . . . . . . . . . . .

• Once again the merits of designing to maintain an orderly, steady flowof air around all external components of the configuration were reaf-firmed. It must be strongly re-emphasized that lightweight structuresare greatly susceptible to fatigue damage accumulation due to sustai-ned unsteady load applications caused by separation and cyclic vortexshedding, and that the noise and airframe responses created by theseare, at best, uncomfortable for the crews who must fly the aircraft.FAIR EVERYTHING IS THE GOOD DESIGN MOTTO, and thentake care that neither adverse pressure gradients nor shock-boundarylayer interactions can undo the good work.

9.1 Strati limite self similari

Vediamo ora di esaminare piu in dettaglio dal punto di vista matematicoalcune semplici soluzioni delle equazioni di strato limite, e piu precisamentequelle corrispondenti agli strati limite cosiddetti self similari. Come vedremoessi corrispondono a flussi esterni molto semplici, e dal punto di vista pratico

46

due almeno tra essi sono particolarmente rappresentativi : quello relativoallo strato limite laminare sulla lamina piana e quello, ovviamente laminare,che si sviluppa a partire da un punto d’arresto regolare.

Abbiamo visto che nel caso di strato limite incompressibile, stazionario,bidimensionale le equazioni di strato limite sono date dalle espressioni

∂u

∂x+∂v

∂y= 0

%u∂u

∂x+ %v

∂u

∂y= −dpe

dx+ µ

∂2u

∂y2(136)

dove pe(x) e la pressione esterna, ed esse vanno risolte sotto le condizioniu = 0, v = 0 per y = 0 e u = Ue(x) per y →∞. Notiamo che la coordinatax ha il significato di coordinata curvilinea lungo il corpo in esame calcolataa partire dal punto di arresto della corrente esterna, la coordinata y dicoordinata normale al corpo, ed inoltre si suppone che, sulla scala dellospessore di strato limite, il flusso esterno si trovi all’infinito. Possiamo anchescrivere alternativamente

dpedx

= −%UedUedx

(137)

con Ue (x) valore della velocita esterna, e cio sia nel caso in cui il flussoesterno e potenziale, sia nel caso di flussi esterni rotazionali non viscosi,in quanto il teorema di Bernoulli e sempre soddisfatto su di una linea dicorrente. Notiamo che lo sforzo di attrito a parete τp e dato dalla espressione

τp = µ

(∂u

∂y

)p

(138)

e che nel sistema (136) compaiono solo le due componenti della velocita ue v, in quanto la pressione e data, essendo quella del flusso esterno pe. Ciosemplifica molto i calcoli e in particolare rende il sistema (136) parabolico,cioe risolubile per avanzamento nella coordinata x.

Prima di procedere alla loro risoluzione ricaviamo una interessante re-lazione dallo studio immediato delle equazioni. A parete, (u = v = 0),abbiamo

µ

(∂2u

∂y2

)p

=dpedx

= −%UedUedx

(139)

dal che si deduce che il profilo di velocita u (y) parte a parete con derivataseconda negativa se la corrente esterna sta accelerando, (pressione esternain diminuzione), mentre per correnti ritardate, (pressione esterna in fase direcupero), la derivata seconda diventa positiva. Da figura (24) si vede che inquest’ultimo caso e inevitabile la presenza di un flesso nel profilo di velocita,dovendo esso raccordarsi all’infinito con la corrente esterna.

47

Vediamo ora come definire lo spessore dello strato limite. Uno spesso-re convenzionale, detto spessore geometrico dello strato limite, e dato dalladistanza dalla parete per la quale la velocita lungo la direzione x raggiungeun valore prefissato, per esempio 0.99Ue oppure 0.995Ue. Indicheremo que-sto spessore genericamente come δg o piu precisamente come δ.99 o δ0.995.Notiamo che in questa definizione c’e un certo grado di arbitrarieta assenteinvece nella definizione dello spessore di spostamento δ∗ definito come

δ∗ =

∫ ∞0

(1− u

Ue

)dy (140)

e dello spessore di quantita di moto ϑ dato da

ϑ =

∫ ∞0

u

Ue(1− u

Ue)dy (141)

mentre il cosiddetto fattore di forma H del profilo di velocita nello stratolimite e dato da

H =δ∗

ϑ(142)

e notiamo che dal punto di vista pratico esse sono abbastanza bene appros-simate dalle espressioni

δ∗ =

∫ δg

0

(1− u

Ue

)dy

ϑ =

∫ δg

0

u

Ue(1− u

Ue)dy

Introduciamo ora il profilo di velocita adimensionalizzato φ definito come

u(x, y)

Ue(x)= φ (x, η) (143)

dove la distanza adimensionale dalla parete η e definita come

η =y

δs(x)(144)

e dove δs e un nuovo spessore, per il momento arbitrario, che chiameremospessore di similitudine. Il significato di questa definizione appare evidentenel momento in cui ci proponiamo di studiare quegli strati limite prodottida quelle particolari correnti esterne Ue(x) per i quali il profilo di velocitau(x, y) e self-similare, per i quali cioe si ha piu semplicemente

u(x, y)

Ue(x)= φ (η) (145)

Se confrontiamo la (143) con la (145) vediamo la grande differenza trale due. L’introduzione delle nuove variabili φ e η nella prima e puramente

48

formale : come la vecchia variabile u dipende da due coordinate, x e y, lanuova variabile φ dipende da due coordinate, x e η. La condizione di selfsimilarita espressa dalla (145) e invece una condizione molto particolare erestrittiva : la nuova variabile φ dipende in questo caso da una sola variabile,η, che prende appunto il nome di variabile di similitudine. La domanda aquesto punto diventa allora la seguente. Esistono correnti esterne per le qualisi formano strati limite self similari ? Al fine di esplorare questa possibilitaintroduciamo la funzione di corrente ψ tale che

u =∂ψ

∂y; v = −∂ψ

∂x(146)

col che la prima delle (136), equazione di bilancio della massa, e automa-ticamente soddisfatta. Per sostituzione si ottiene poi dalla seconda delle(136)

∂ψ

∂y

∂2ψ

∂y∂x− ∂ψ

∂x

∂2ψ

∂y2= Ue

dUedx

+ ν∂3ψ

∂y3(147)

e al fine di risolvere questa equazione introduciamo le nuove variabili

ξ = x ; η =y

δs(148)

e la funzione di corrente adimensionale

f (ξ, η) =ψ

Ueδs(149)

riservandoci sempre di definire piu precisamente in seguito l’andamento conla coordinata x = ξ dello spessore di similitudine δs = δs (x). Nei terminidelle nuove variabili si ha

u =∂ψ

∂y= Uef

′

∂2ψ

∂y2=

Ueδsf

′′

∂3ψ

∂y3=

Ueδ2sf

′′′

−v =∂ψ

∂x= f

d (Ueδs)

dx− f ′

ηUedδsdx

+ Ueδs∂f

∂ξ

∂2ψ

∂x∂y= f

′ dUedx− f ′′

ηUeδs

dδsdx

+ Ue∂f

′

∂ξ(150)

dove l’apice indica la derivazione rispetto ad η. Se inseriamo queste espres-sioni nella (147) si ottiene l’equazione

f′′′

+ff′′ δsν

d (Ueδs)

dx+(1− f ′

f′) δ2sν

dUedx

=Ueδ

2s

ν

(f

′ ∂f′

∂ξ− f ′′ ∂f

∂ξ

)(151)

49

e possiamo ora vedere sotto quali condizioni di corrente esterna Ue questaequazione ammette soluzioni self similari, tali cioe che dipendono dalla solavariabile di similitudine η,

f = f

(y

δs

)(152)

Fisicamente cio significa chiedersi per quali particolari correnti esterne sihanno profili di strato limite che si conservano uguali a se stessi lungo ilcorpo se opportunamente scalati con la x e la y

u

Ue= f ′

(y

δs

)(153)

e si puo vedere facilmente che si hanno le soluzioni cercate nel caso in cuil’andamento della corrente esterna a partire dal punto di arresto x = 0 edato da

Ue = axm (154)

con a ed m costanti e per una scelta di δs tale che

δsx

=1√Uex

ν

=1√Rex

(155)

Svolgendo i calcoli si ottiene allora

f′′′

+m+ 1

2ff

′′+m

(1− f ′

f′)

= 0 (156)

dove ora la derivata in η, variabile di similitudine, e diventata una derivataordinaria, mentre le condizioni al contorno per f (η) sono f = f

′= 0 per

η = 0 e f′

= 1 per η →∞, essendo nei termini di f

u =∂ψ

∂y= Uef

′

v = −∂ψ∂x

= −f d (Ueδs)

dx+ f

′ηUe

dδsdx

(157)

I flussi potenziali esterni ai quali corrispondono le correnti date dalla(154) sono rappresentate in figura (25). Fisicamente essi sono i flussi intornoa diedri investiti da una corrente uniforme all’infinito, e l’apertura del diedroβ in termini di π e legata all’esponente m dalle relazioni

β =2m

m+ 1m =

β

2− β(158)

Notiamo che mentre il coefficiente m e esclusivamente legato all’apertura βdel diedro, il coefficiente a dipende sia dal valore della corrente indisturbata

50

a monte sia dalla geometria successiva del corpo considerato. Per rendercenemeglio conto consideriamo i flussi del tipo

Ue = ax (159)

con esponente m = 1, e notiamo che qualsiasi flusso esterno piano, in pros-simita del punto d’arresto, e approssimabile da una espressione del genere,a patto che il punto di arresto sia un punto regolare, vedi figura (26). Inquesto caso il coefficiente a e dato dal primo termine della espansione inserie di Taylor del flusso esterno considerato, abbiamo cioe che

Ue =

(dUedx

)0x (160)

dove l’indice 0 significa che la derivata e calcolata nel punto di arresto, x = 0.A titolo di esempio abbiamo per il flusso intorno ad un cilindro,

Ue = 2U∞ sin

(x

R

)=

2U∞R

x+ ..... (161)

da cui si deriva che in corrispondenza ad un bordo di attacco cilindrico ilcoefficiente a ha il valore 2U∞/R, dove R e il raggio del cilindro stesso e U∞il valore della velocita della corrente indisturbata.

Consideriamo ora il caso in cui m = 0, che corrisponde al flusso di stratolimite sulla lamina piana, vedi figura (27). In tal caso l’equazione (156)assume la forma

f′′′

+ff

′′

2= 0 (162)

e la sua soluzione, ottenuta per la prima volta da Blasius, e stata in seguitopiu volte migliorata e verificata In tabella (1) vengono riportati i valoricalcolati da Howarth, e nelle figure (28) e (29) sono graficati i profili divelocita per la u e la v. Infine in figura (30) sono riportati i confronti tra ilprofilo di Blasius e quello sperimentale. Tabella e figure sono tratte dal testodello Schlichting, Boundary Layer Theory, al quale si rimanda per ulterioridettagli. Notiamo che nei termini di f(η) l’espressione del coefficiente diattrito locale cf e data da

cf =τp

12%U

2e

=2f ′′(0)√Rex

(163)

essendo

τp = µ

(∂u

∂y

)p

= µ

(∂2ψ

∂y2

)p

= µUef

′′(0)

δs(164)

L’espressione delle spessore di spostamento δ∗ e data da

δ∗ =

∫ ∞0

(1− u

Ue

)dy = δs

∫ ∞0

(1− f ′

)dη (165)

51

per cui

δ∗ = δs limη→∞

(η − f) (166)

mentre lo spessore di quantita di moto ϑ e dato da

ϑ = δs

∫ ∞0

f ′(1− f ′)dη =2δs

3m+ 1

(f ′′(0)−mδ∗

δs

)(167)

Quest’ultima relazione puo essere ricavata notando che dalla equazione (156)si ottiene∫ ∞

0f ′f ′dη =

∫ ∞0

f ′′′

mdη +

∫ ∞0

dη +m+ 1

2m

∫ ∞0

ff ′′dη (168)

e che ∫ ∞0

f ′f ′dη =

∫ ∞0

f ′df = (f ′f)∞ − (f ′f)0 −∫ ∞0

ff ′′dη (169)

Vediamo ora i casi in cui l’esponente m e diverso da zero. Le soluzionirelative sono state ottenute da Falkner e Skan, ed anche in questo casoriportiamo i risultati tratti dal testo dello Schlichting, vedi figura (31), enotiamo che in questo grafico lo spessore geometrico di similitudine δs eposto uguale a

δsx

=

√2

m+ 1

1√Uex

ν

(170)

E’ interessante notare come i profili siano sempre piu stirati nel verso dellacorrente, e quindi sempre piu stabili, per correnti acceleranti, mentre percorrenti deceleranti, cioe in gradiente di pressione avverso, si ha l’immediatanascita di un flesso e la separazione a parete per m = −0.091.

Nella tabella che segue sono riportati per vari valori dell’esponente mil valore del coefficiente locale di attrito cf riferito alla corrente esterna edefinito come

cf =τp

12%U

2e

(171)

e i valori dello spessore di spostamento δ∗, dello spessore di quantita di motoϑ e del fattore di forma del profilo H.

m cf√Rex

δ∗

x

√Rex

ϑ

x

√Rex H =

δ∗

ϑ0 0.664 1.721 0.664 2.591 2.465 0.648 0.292 2.22-0.091 0.0 3.428 0.868 3.94

52

Ricordiamo che la corrente esterna Ue e il numero locale di Reynolds adessa riferito Rex sono dati da

Ue = axm Rex =Uex

ν(172)

e notiamo che il fattore di forma diminuisce per correnti acceleranti ed au-menta per correnti deceleranti raggiungendo il valore di circa 4 alla sepa-razione. E’ interessante anche notare il diverso andamento dello sforzo diattrito a parete τp sulla lamina piana, m = 0, e in prossimita di un bordod’attacco regolare piano, m = 1. Da figura (32) si puo notare che nel primocaso esso parte da un valore infinito, ma integrabile, essendo proporzionalea

τp ∝ x−12 (173)

mentre nel secondo caso l’andamento e lineare, avendosi

τp ∝ x (174)

Per quel che riguarda l’andamento dello spessore di strato limite δ abbiamoinvece, vedi sempre figura (32)

δ ∝ x12 (175)

sulla lamina piana, mentre in vicinanza di un punto d’arresto regolare lospessore di strato limite resta costante ed uguale al valore che ha per x = 0

δ ∝√√√√ νdUedx

(176)

Piu precisamente abbiamo per quel che riguarda lo spessore di spostamentoδ∗

δ∗ = 0.648

√√√√ νdUedx

(177)

per cui su di un cilindro di raggio R investito da una corrente all’infinitoU∞ si ha

δ∗ = 0.648

√νR

2U∞(178)

53

Riferimenti bibliografici

[1] P. Rebuffet (1958) Aerodynamique Experimentale Librairie Polytechni-que Ch. Beranger, Paris et Liege

[2] B. McCormick (1979) Aerodynamics, Aeronautics and Flight MechanicsJohn Wiley and Sons, New York

[3] L. I. Sedov, (1959) Similarity and Dimensional Methods in MechanicsInfosearch LTD, London

[4] Ya. B. Zel’dovich, Yu. P. Raizer, (1966) Phisics of Shock Waves andHigh Temperature Phenomena Academic Press, New York and London

[5] Autori vari, (1983) Shuttle Performance:Lessons Learned NASA CP2283 Part I and II

[6] H. Schlichting, (1955) Boundary Layer Theory Pergamon Press, London

[7] M. Van Dyke, (1982) An Album of Fluid Motion The Parabolic Press,Stanford CA

[8] G. K. Batchelor, (1967) An Introduction to Fluid Dynamics CambridgeUniversity Press, Cambridge

[9] F. M. White, (1974) Viscous Fluid Flow Mc-Graw Hill, New York

54

55

56

57

58

$#

\

\ \

\ \ \

\ \ \

\ \ \\ \

\

F:,f. +A'r^"' 1..oFoo-,,o?a./

F. R: t Pt "to" ' *l*.ì-,,*?"

s. L. al-.",f" ' T,*,lo

.0lq -tt) c )

- - _ +

:ù' ; -

-

,.: it:

\

f tq J,zl o

59

l r c ./ d

f3

! r q ./ d

l tt 1

60

' s $

l i t r : . i $ . S r r r r . t . s s i l u l r l r o t r r g r r r p l r s , r l ' t l r r : l ì n ' l x r l l l i r r r r r / i l . I X l l F r .. l ' t l l l , : l l ) - r s r . c . i r r r r r r r t l o u r i r l x r r n l r t s P l o s i o r r i r r - \ c r r . ] l t . s i r . u .

-l iq. J5) o

("r st,

61

l iq tG) u

u (u)

\ I F

l 1 8

,(l) , (g)

e î - : , . "

62

,0f

L oÉ'R îe'"/- ltafazie"+k-. - - . --

I

. i r

s . L . t .S . L . T .

T.s . L .s.T.

G.e < 2x toí

G " > 1 x r c 5

SrJ" tù^;lt' P,'*';,*,*sh-.|, Q;lulz,*><z-Lev&

S'l*ra,.ioru U.*-sJ,,,,n^ú.*" Itq.%?a,l*

f'Í jg

- - - r P

(1'j

--- f , j , . :

63

- S h u c E l e c a r r i e r a i r c r a f c d u r i . n g A L T f l i g h c i n I 9 7 7 .

scn Shuli%. 6*ìu fr;n*pFRLT fi. in,n?-"',J-l-,ht T^l

d

-0iqt d

- P a n e l i n g f o r p o c e n c i a l f l o w a n a l y s i s .

ia',,

/ r q a a \\ , . " " /frhu,,ce

l < )| F J +ftAl/te,

l nóa,Y , lrasn cP 2283

64

CYLINDRICALSUPPORTS

I J r nl a ' 2L

SHUITLEINCIDENCE

4 0 1 5 '

_l

- E a r l y S C A c o n f i g u r a E i o n .

EFIN

xrENstoì/

f iq' c /

- F i n a l S C A c o n f i g u r a c i o n .

lGsn cP ,2 83

L3

SHUTTLEINCIDENCE

FINS,2OO SQ FT

figuzeÌ- rLt?,o, I lg d"",P (r sss)

65

]tr

's )

I ^"| ùto-z-L<n'-e- 4'*1"

à* D I L€,forc.o,to\

L(ot:zz^le-

Iú?/\Q/A^e-

.;-u?rr.Jo

,**lorn;r-

Jr*?rÀ,) o.**'l-e., , h n

VPtu*" J^ u4 f1'/Yra

I

- .È . .

66

--t't-,

t ) |I L

Q ùtl€,>loi

l . tà*eÀz*

l^Latt

4) "P

f's 2tJ'r**1,

oà,* g'

' Lfu-vt

ro

)cEa

(P= r ) "-+--. . . . . . ./ \

t ^ ì

f l $ = o It , I\ / . /lrt*".

l; rB

t.u

i - t l r t t

u.o

0.+

u.z

N R

v ì ,U . - xu*y v

U.,|

f.l 2s1 5 6

,'4'Ej - î | - . 1

,1 J

1 2 3

67

4-, j : yi/-ú.*. l ' , z (/ È.: \J*AL !

3.431S93.6S0943.Ss03l4'079904-27964

4 479484.6?9334.S79315.079235.27926

5.4i9255.6i9245.s79!4'6.079236.2i923

6.479236.67S236.S79237.07923

00.90.4u 'o0.sI .0

t . 2l . a

i . 32 .0

9 . '

2 .49 . 4

2-SJ ' U

3.23 .4

. J O

3.84.0

4.24.44.64.35.0

00.(x1660.026560.059740.1061 Iu' .t, oJJ r

0.23;950.3229S0.420320.529520.65003

0'-rS 1200.922301.07252r.230991.39652

r.5691i1.746961.929542.1 I 6052.30576

2-49S062.6923s2.SSS263.0s5343.2S329

00.066410.1 3 !7?0. r 9s940.2647 I0.329?9

0.3937S0.456270.516;60-514ii0.62977

0.6s i320-72S990.772460.s t 1520.s4605

0.s76090.901770.923330.941120.95552

0.966960.975S70.9s2690.9s7790.99r55

0.332060.33 r 990.3314?0.3300s0.327390-32301

U . ó T U J V

0'307s70-296670.2s2930.266?5

0.24S3ó0.22S090.206460.ts40lu ' t u róo

0.139t30. l17ss0.09s090'0s0r30.06424

0.050520.03.s970.0294S0.021s70.01591

0.994250.996160.997480.99833n.ooaoa

n.oooît0.9996t0.999770.999S7n.oooo.)

0.99S960.999980'99999r 000001.00000

t'00000I'0000,0r.00000l.Cú.,v((l

0.0t t340 007930.005430.003650.00240

U'UUI AD0.000930.0006r0.000370.N)022

0.000t30-000070.000040'000020-0000I

0.wnl0.000cn0.000000.u..100

< . t5 -4c 'o5 '86.0

6 . 26.46 .66 . 8t . u

7 . 27 .4, , 'o

8.2s.43 .6s.s

f,,q.l a

,.: ia;:

3o

68

3i,l ìol d '

|'^"-r)/tuu;/t L

úi,uanza. Vl" J_'onn*,Fo ,r7"g,-

69

APPUNTI DI GASDINAMICA

CAPITOLO 3

EQUAZIONI MEDIATE PER I FLUSSI

TURBOLENTI

M. GermanoDip. di Ing. Aeronautica e Spaziale

Politecnico di Torino

1

Contents

1 Instabilita e turbolenza 3

2 Studio statistico della turbolenza. Equazioni di Reynolds. 4

3 Il problema della chiusura. L’ipotesi di Boussinesq. Il mod-ello Kt − ε per la viscosita turbolenta. 10

2

1 Instabilita e turbolenza

Come abbiamo gia detto in precedenza molte delle soluzioni esatte trovatesono valide solo per numeri di Reynolds del flusso inferiori ad un valorecritico. Al di sopra di questo si manifestano instabilita, e rapidamente ilflusso diventa caotico. Cio significa che le componenti della velocita e lapressione fluttuano nel tempo, che il flusso diventa tridimensionale e non-stazionario e che quindi una descrizione dettagliata diventa estremamentecomplessa e richiede una enorme informazione. Fortunatamente se le con-dizioni al contorno sono fisse il flusso resta stazionario in media, dove permedia si intende quella temporale, come sara meglio precisato in seguito.Una prima proprieta fondamentale della turbolenza e in questo caso quellodi conservare eventuali simmetrie del flusso, (planarita, assialsimmetria),ma sempre per quel che riguarda i valori medi: le instabilita distruggono lastruttura laminare del flusso ma il caos che subentra coopera a creare unmoto medio non molto diverso come struttura da quello laminare.

Dal punto di vista matematico la turbolenza viene interpretata alla lucedelle teorie dei sistemi dinamici a molti gradi di liberta e sul comportamentodei loro punti fissi, cioe delle loro soluzioni stazionarie, al variare di qualcheparametro di controllo, con conseguente perdita di stabilita e nascita dioggetti molto complessi, non stazionari e caotici detti attrattori strani. Unflusso e infatti assimilabile ad un sistema dinamico a moltissimi gradi di lib-erta. Esso ammette soluzioni stazionarie, laminari, i punti fissi, per ogni nu-mero di Reynolds, ma al di la di un valore critico esse perdono ogni significatoessendo instabili e dando luogo a una nuova struttura, nonstazionaria, caot-ica, in cui i valori di velocita e pressione fluttuano aperiodicamente intornoa valori medi dentro il cosiddetto bacino di attrazione della nuova soluzione.Dal punto di vista fisico e come se all’equilibrio stazionario del flusso lam-inare considerato si sostituisca invecchiando un nuovo equilibrio, dinamico,piu possibilista e accomodante. Notiamo infatti che se da un lato ai flussiturbolenti corrisponde generalmente un aumento di resistenza d’attrito, par-ticolarmente per quel che riguarda i flussi di strato limite, dall’altro si haun notevole vantaggio per quel che riguarda mescolamenti di fluido e aggira-menti di ostacoli, con notevoli diminuzioni per quel che riguarda la resistenzadi forma. Senza la diffusione turbolenta gli effetti diffusivi sarebbero lentis-simi e le separazioni molto piu anticipate, e in fondo si puo dire che l’effettopiu caratterizzante della turbolenza e quello di aumentare fortemente tuttii fenomeni di trasporto.

3

2 Studio statistico della turbolenza. Equazioni diReynolds.

Lo studio della turbolenza avviene oggi essenzialmente in due modi. Il primoe quello diretto, nel quale le equazioni del moto sono studiate in tutti i lorodettagli e vengono ricercate soluzioni, generalmente di natura numerica,dette simulazioni dirette. Il secondo e quello mediato, in cui si definisconooperativamente nuove grandezze, apparentemente piu semplici di quelle orig-inali, e nei termini delle quali si scrivono le nuove equazioni evolutive. Dataper esempio la grandezza turbolenta, caotica, f (~x, t′), viene spontaneo rin-unciare alla sua precisa determinazione e rassegnarsi alla sola determinazionedei valori medi temporali

f (~x) = limT→∞

1

2T

∫ t+T

t−Tf(~x, t′

)dt′ (1)

E’ chiaro che la dipendenza temporale dal tempo viene in tal modo eliminata,e se indichiamo al solito 2 con l’apice le fluttuazioni, si puo scrivere per lecomponenti della velocita e la pressione

u = u+ u′ v = v + v′ w = w + w′ p = p+ p′ (2)

e valgono le seguenti proprieta

u′ = 0 uu = uu+ u′u′ · · ·

∂u

∂t=∂u

∂t= 0

∂u

∂x=∂u

∂x· · · (3)

Se ora procediamo in questa direzione andiamo incontro a due problemifondamentali. Il primo e dovuto al fatto che le medie che normalmentevengono misurate sono le medie temporali, mentre la statistica e basatafondamentalmente sul concetto di medie d’insieme. A questo proposito sipuo notare che nel caso di turbolenza statisticamente stazionaria le medietemporali possono essere considerate anche come medie di insieme, quellecioe che otterrei ripetendo la stessa esperienza in diverse gallerie del vento.

2Non si confonda questa nuova operazione di media con quella fatta sulle molecole eche ci ha permesso di ricavare le equazioni di bilancio. La tecnica statistica e sempre lastessa, ma gli oggetti e le scale sono ovviamente molto diverse. La si trattava di mediaresu di una funzione di distribuzione molecolare e le fluttuazioni erano a livello del liberocammino medio, qui si tratta di mediare nel tempo e le fluttuazioni sono su tempi moltopiu lunghi di quelli intercorrenti tra due urti molecolari.

4

Il discorso e molto complesso, e coinvolge il cosiddetto teorema ergodico.Dato un sistema dinamico non e affatto semplice dimostrare l’equivalenzatra medie temporali e medie d’insieme : spesso questa identita si postula,e sostanzialmente si basa sull’ipotesi che il lancio di un milione di dadi siastatisticamente equivalente a lanciare un dado un milione di volte. Il secondoproblema e dovuto al fatto che e relativamente facile mediare dei segnali, mae molto piu complesso mediare delle equazioni. Se infatti vogliamo descriverela turbolenza nei termini di valori medi, allora dobbiamo costruirci le relativeequazioni di bilancio a partire dalle equazioni di Navier-Stokes, e questo etutt’altro che facile e come vedremo tutt’altro che ben definito dal punto divista matematico.

Mediare delle equazioni ha richiesto molto coraggio e molta fantasia daparte dei ricercatori interessati allo studio della turbolenza. Il primo cheli ebbe fu Osborne Reynolds [1], e le equazioni di Navier-Stokes mediateportano il suo nome. Notiamo che dal punto di vista formale non e in realtacosı difficile mediare le equazioni di bilancio. Se infatti applichiamo ad esse

∂u

∂x+∂v

∂y+∂w

∂z= 0 (4)

∂%u

∂t+∂%uu

∂x+∂%uv

∂y+∂%uw

∂z= −∂p

∂x+ µ

(∂2u

∂x2+∂2u

∂y2+∂2u

∂z2

)(5)

l’operatore di media temporale seguendo le regole della media precedente-mente definite (3) otteniamo formalmente

∂u

∂x+∂v

∂y+∂w

∂z= 0 (6)

∂%uu

∂x+

∂%vu

∂y+∂%wu

∂z= −∂p

∂x+ µ

(∂2u

∂x2+∂2u

∂y2+∂2u

∂z2

)−

− ∂%u′u′

∂x− ∂%u′v′

∂y− ∂%u′w′

∂z(7)

dove per semplicita si e considerato il flusso incompressibile e si e scrittal’equazione mediata della quantita di moto per la sola componente lungola direzione x, (le altre due sono ovviamente derivabili per permutazioneciclica).

5

Notiamo che esse differiscono da quelle precedenti per via di un nuovotermine che ha le caratteristiche di una forza per unita di volume e in cuicompaiono i cosiddetti sforzi di Reynolds Rxx, Rxy, Rxz

Rxx = −%u′u′ Rxy = −%u′v′ Rxz = −%u′w′ (8)

e vediamo subito che il processo di media ha ovviamente lasciato inalteratoil numero delle equazioni, ma ha aumentato il numero delle incognite perchegli sforzi di Reynolds sono calcolabili solo a partire dalla conoscenza direttadella turbolenza, e non sono certo determinabili dalle equazioni mediate so-prascritte. Il problema di risolvere queste equazioni e il cosiddetto problemadella chiusura, dove per chiusura si intende la formulazione di un modellodi turbolenza che esprima gli sforzi di Reynolds in funzione dei valori medi.Un modo per ovviare a questo inconveniente sembrerebbe essere quello discrivere le equazioni evolutive per questi sforzi turbolenti aggiuntivi, masi puo facilmente vedere che cio complica ulteriormente le cose. Se infattiscriviamo per differenza le equazioni di bilancio delle fluttuazioni di massae di quantita di moto otteniamo che

∂u′

∂x+∂v′

∂y+∂w′

∂z= 0 (9)

∂%u′

∂t+

∂%u′u′

∂x+∂%v′u′

∂y+∂%w′u′

∂z= −∂p

′

∂x+

+ µ

(∂2u′

∂x2+∂2u′

∂y2+∂2u′

∂z2

)− ∂(%u′u+ %uu′ − %u′u′)

∂x−

− ∂(%u′v + %uv′ − %u′v′)∂y

− ∂(%u′w + %uw′ − %u′w′)∂z

(10)

Provvisti delle equazioni di bilancio per le grandezze fluttuanti e ora rel-ativamente facile con passaggi algebrici e mediando ottenere le equazioni dibilancio degli sforzi di Reynolds e piu in generale di qualsiasi altra grandezzamedia, ma una volta scritte queste equazioni rivelano la complessita delproblema, in quanto in esse compaiono altre nuove grandezze incognite chenon permettono di avere mai un numero di equazioni pari a quello delleincognite. Introduciamo la notazione compatta

−%u′iu′j = Rij (11)

6

e scriviamo che∂uk∂xk

= 0 (12)

∂%uiuk∂xk

= − ∂p

∂xi+ µ

∂2ui∂x2k

+∂Rik∂xk

(13)

∂%u′i∂t

+∂%u′iu

′k

∂xk= − ∂p

′

∂xi+ µ

∂2u′i∂x2k

−

−∂(%u′iuk + %uiu

′k − %u′iu′k)

∂xk(14)

e che

∂%u′j∂t

+∂%u′ju

′k

∂xk= − ∂p

′

∂xj+ µ

∂2u′j∂x2k

−

−∂(%u′j uk + %uju

′k − %u′ju′k)

∂xk(15)

dove si intende che l’indice ripetuto e sommato. Moltiplichiamo ora la (14)per u′j e la (15) per u′i, sommiamo e mediamo. Si ottiene con qualchepassaggio algebrico e tenendo conto che la media della derivata temporale enulla

DRijDt

= uk∂Rij∂xk

= %Pij +∂Dijk

∂xk+ ϕij − %εij + µ

∂2Rij∂xk∂xk

(16)

dove

Pij = −Rik%

∂uj∂xk− Rjk

%

∂ui∂xk

(17)

rappresenta la produzione per unita di massa e di tempo

Dijk = %u′iu′ju′k + p′u′jδik + p′u′iδjk (18)

rappresenta la diffusione

ϕij = p′

(∂u′i∂xj

+∂u′j∂xi

)(19)

rappresenta la ridistribuzione operata dalle fluttuazioni di pressioni e doveinfine

εij = −2ν∂u′i∂xk

∂u′j∂xk

(20)

7

rappresenta la dissipazione. Se ora indichiamo con

Kt =u′iu′i

2= −Rii

2%(21)

l’energia cinetica turbolenta per unita di massa si ottiene infine per con-trazione dell’equazione precedente

%DKt

Dt= %uk

∂Kt

∂xk= %P +

∂Dk

∂xk− %ε+ µ

∂2Kt

∂xk∂xk(22)

dove ora P rappresenta la produzione di energia cinetica turbolenta perunita di massa e di tempo

P =Rik%

∂ui∂xk

(23)

Dk la diffusione

Dk = −%u′iu′iu′k

2− p′u′k (24)

ε la dissipazione, cioe l’energia turbolenta dissipata per unita di massa e ditempo

ε = ν∂u′i∂xk

∂u′i∂xk

(25)

e dove la ridistribuzione e nulla, essendo per un flusso turbolento incom-pressibile

∂u′i∂xi

= 0 (26)

Notiamo ora che l’energia cinetica turbolenta per unita di massa Kt

Kt =

(u′u′ + v′v′ + w′w′

)2

(27)

di cui sopra abbiamo scritto l’equazione di bilancio, ci fornisce una scala divelocita vt della turbolenza in quanto possiamo scrivere

vt ' K12t (28)

e questa scala di velocita insieme ad una scala di lunghezze indicativa delledimensioni dei grossi vortici lt costituiscono la cosiddetta macroscala delflusso turbolento in esame. La lunghezza lt viene anche detta lunghezza dimescolamento, e su questa scala avviene da parte della turbolenza la cattura

8

di energia ordinata grazie essenzialmente ai vortici piu grossi che attraversola cascata inerziale la trasferiscono a vortici sempre piu piccoli fino alla cosid-detta microscala, o scala dissipativa. E’ infatti peculiare della turbolenzaaccelerare i processi dissipativi grazie a meccanismi inerziali paragonabili aquelli che mettiamo in gioco quando succhiamo una caramella. Chi sciogliee dissipa e la saliva, ma certamente il processo viene accelerato dalla fran-tumazione meccanica della caramella in piccoli pezzi attraverso i denti. Alivello di microscala interviene finalmente la viscosita, e solo a questo livello.Dal punto di vista energetico la turbolenza puo quindi essere interpretatacome uno scambio energetico tra il moto medio e il moto caotico che assi-cura la stabilita del fluido. La quantita di energia ε per unita di massa e ditempo scambiata tra questi due moti e come abbiamo visto la dissipazioneturbolenta, ε e da quanto detto essa assume un ruolo centrale nello studio deiflussi turbolenti. Considerazioni dimensionali dovute al Taylor permettonodi stimare ε a partire dalle grandezze di macroscala vt e lt

ε ' v3tlt

(29)

e notiamo che questa grandezza non va assolutamente confusa con l’energiaturbolenta Kt precedentemente definita. Grossolanamente si puo dire che laenergia cinetica turbolenta da una idea di quanto grande sia la possibilita cheun flusso ha di macinare inerzialmente i grossi vortici, mentre la dissipazioneviscosa indica quando grande sia la possibilita di smaltire i rottami deglistessi.

Attraverso la dissipazione viscosa ε precedentemente definita si puo an-che fare una stima della scala di lunghezze dissipativa, o microscala, lm. An-che questa stima avviene su pure considerazioni dimensionali, ed e dovutaessenzialmente al Kolmogorov. Se infatti supponiamo che la lunghezza dimicroscala lm dipenda unicamente dalla viscosita molecolare ν e dalla dissi-pazione turbolenta ε, con semplici considerazioni dimensionali otteniamo

lm '(ν3

ε

) 14

(30)

mentre la velocita di microscala vm si ottiene grazie al fatto che a livellodissipativo il Reynolds relativo deve essere dell’ordine dell’unita

Rem =vmlmν' 1 (31)

9

Possiamo in conclusione tracciare la tabella (1) che illustra le varie scalefisiche, a partire da quelle molecolari a quelle turbolente fino ad arrivarealle scale geometriche generalmente definite nei termini di una velocitaall’infinito U e di una lunghezza caratteristica del corpo L. Ricordiamoche la velocita di propagazione del suono e la velocita di agitazione termicavat sono dello stesso ordine di grandezza e che la viscosita molecolare ν edata dal prodotto di quest’ultima per il libero cammino medio molecolare l

ν ' lvat (32)

Lunghezze Velocita Tempi

Scala geometrica L U T = L/UMacroscala turbolenza lt vt Tt = lt/vtMicroscala turbolenza lm vm Tm = lm/vmScala molecolare l vat ϑ = l/vat

Table 1: Scale fisiche

3 Il problema della chiusura. L’ipotesi di Boussi-nesq. Il modello Kt − ε per la viscosita turbo-lenta.

Abbiamo visto che le equazioni mediate contengono piu incognite di quelledi partenza, il che matematicamente corrisponde ad un problema indeter-minato. Occorre chiudere con opportune ipotesi il sistema di equazioni ot-tenuto, cioe ridurre il numero di grandezze incognite oppure aumentare il nu-mero delle equazioni. Prima di vedere come si possono modellare le equazioniche descrivono in media i flussi turbolenti e opportuno esaminare la loronatura fisica. Notiamo che a questo proposito il piu potente metodo di stu-dio e sempre quello diretto, in cui le equazioni di Navier-Stokes sono risoltein tutti i dettagli. Per far cio occorre tuttavia avere una risoluzione numer-ica molto elevata, e piu particolarmente una dimensione di griglia di calcolodell’ordine della lunghezza di microscala lm. Con gli odierni mezzi di cal-colo cio e possibile solo per bassissimi numeri di Reynolds, e i primi risultatiottenuti confermano i comportamenti tratteggiati nelle sezioni precedenti.

10

Ripetiamo che la turbolenza e dal punto di vista energetico un fenomenodissipativo. Energia fresca, coerente, di larga scala, dovuta a fluttuazioni dilungo periodo e di grandi lunghezze d’onda viene macinata attraverso unacascata inerziale in fluttuazioni vorticose sempre piu piccole fino a che noninterviene la viscosita a dare il colpo di grazia. Ricordiamo che la cascataviene detta inerziale perche in essa non si ha sostanzialmente alcuna dis-sipazione, e solo la viscosita dissipa, trasformando in calore, ma e chiaroche essa e essenziale al fine di trasformare le grosse strutture vorticose instrutture piu piccole e piu facilmente digeribili.

Vediamo ora come esprimere in termini espliciti gli sforzi di ReynoldsRij , cioe, come si dice usualmente, di modellarli. Il carattere dissipativodella turbolenza e la natura degli sforzi di Reynolds suggeriscono analogiecon quello che e il moto caotico molecolare. Ricordiamo che gia una voltaci siamo trovati di fronte a termini del tipo %u′v′, con la sola differenza cheallora le fluttuazioni di velocita erano a livello molecolare, mentre ora essesono sostanzialmente a livello della scala turbolenta. Il tensore di Reynolds ecomunque composto da termini che rappresentano flussi di quantita di mototrasportati dalla agitazione turbolenta, e se applichiamo gli stessi ragiona-menti applicati all’analisi della agitazione molecolare vediamo che formal-mente si puo scrivere

Rij ' −2

3%Ktδij + 2µtsij (33)

dove la parte anisotropa degli sforzi turbolenti viene fatta dipendere daltensore mediato delle deformazioni di velocita sij

sij =1

2

(∂ui∂xj

+∂uj∂xi− 2δij

3

∂uk∂xk

)(34)

attraverso una viscosita turbolenta µt. Questa ipotesi, che porta il nomedi ipotesi di Boussinesq, pone in analogia l’agitazione turbolenta con quellatermica, e la viscosita turbolenta con quella molecolare dove alla velocita diagitazione termica vat e sostituita per analogia una velocita di macroscala, ovelocita di agitazione turbolenta vt, e al libero cammino medio collisionale latuna lunghezza di macroscala, o lunghezza di mescolamento lt. La conclusionee che strutturalmente le equazione mediate restano uguali a quelle di Navier-Stokes, tranne il fatto che la viscosita e aumentata di una viscosita turbolentaµt data da

µt ' %vtlt (35)

11

ed e chiaro che il problema e ora quello di determinare vt ed lt. Primadi far cio notiamo che l’analogia con l’agitazione molecolare mette in luceun altro peculiare fatto della turbolenza, e cioe la sua naturale tendenzaad aumentare il mescolamento tra le masse fluide. E’ tuttavia importantesottolineare che questa analogia va presa con molta cautela, e non e fuordi luogo vedere ora quali sono le fondamentali differenze tra l’agitazionemolecolare e quella turbolenta. Notiamo subito che non esiste una termodi-namica della turbolenza, al contrario della agitazione termica in cui avevamodistinto tra situazioni di equilibrio e non. L’analogia e per cosı dire a livellodi termocinetica della turbolenza, in quanto occorre sempre ricordare chela turbolenza e dal punto di vista energetico un fenomeno dissipativo, chequindi non si puo sostenere senza delle forzanti che la alimentano estraendoenergia fresca dal moto medio e senza la presenza della viscosita che dis-sipa al termine della cascata inerziale. La conseguenza e che non esiste unauna equazione di stato che leghi l’energia turbolenta Kt alle altre grandezzetermodinamiche, e il problema quindi si presenta estremamente piu compli-cato. Se infatti procediamo nella analisi di questa analogia vediamo che alivello della agitazione molecolare proprio questi legami termodinamici ave-vano permesso di ricavare facilmente la velocita di agitazione termica vat edi legarla alla temperatura assoluta locale. Inoltre la lunghezza caratter-istica sulla scala molecolare e una grandezza ben precisa, data fisicamentedal libero cammino medio collisionale l pure esso ricavabile dai valori dellasezione d’urto molecolare e dalla densita locale. Nel caso della agitazioneturbolenta tutto cio perde di significato e nuovi criteri per la determinazionedi vt e lt si impongono. Occorre subito notare che questi criteri sono an-cora notevolmente arbitrari, e che un modello razionale di turbolenza per ilmomento non esiste ancora. Si fanno delle ipotesi, si controllano i risultaticon con le esperienze e si applicano i modelli di turbolenza ottenuti a situ-azioni di progetto abbastanza simili tra loro. Un modello tra i tanti che estato sviluppato in notevole dettaglio e che viene applicato su larga scala eattualmente il modello Kt − ε. Il modello Kt − ε e un modello cosiddettodifferenziale in quanto per determinare la viscosita turbolenta si risolvonoappunto due equazioni differenziali per queste due grandezze. Dal puntodi vista fisico esso si rifa alla visione energetica della turbolenza, cascatainerziale piu dissipazione viscosa. Come abbiamo visto in precedenza le duegrandezze piu significative a questo proposito sono l’energia turbolenta perunita di massa Kt e la dissipazione ε, energia dissipata per unita di massae di tempo. Ricordiamo le relazioni che permettono di ricavare da esse una

12

velocita di macroscala o di mescolamento data da

vt ' K12t (36)

e una lunghezza di macroscala o di mescolamento lt data da

lt 'K

32t

ε(37)

per cui si ottiene una viscosita turbolenta data da

µt = cµ%K2t

ε(38)

dove cµ e una costante numerica. Come abbiamo visto in dettaglio per Kt

lo studio dei momenti di ordine superiore delle equazioni di Navier-Stokesmediate permette di ricavare due equazioni di bilancio per Kt e per ε cheaccoppiate con opportune ipotesi di chiusura vanno risolte accoppiate a con-dizioni al contorno spesso non facili da imporre. Nel modello standard Kt−ε[4] esse hanno la seguente forma

%DKt

Dt=

∂

∂xj

((µ+

µtσk

)∂Kt

∂xj

)+ %P − %ε

%Dε

Dt=

∂

∂xj

((µ+

µtσε

)∂ε

∂xj

)+

ε

Kt

(cε1%P − cε2%ε

)(39)

dove P , produzione di energia turbolenta per unita di massa, e data da

P =Rij%

∂ui∂xj

(40)

e dove σk, σε, cε1, cε2 sono quattro costanti numeriche. Le due equazioni pos-sono essere lette nel seguente modo : a sinistra c’e il termine di trasporto con-vettivo e a destra il termine diffusivo e il termine di produzione. Quest’ultimoe a sua volta diviso in due parti, il termine di produzione vero e proprio e iltermine di produzione negativa, e cioe di dissipazione. Nel caso del bilanciodell’energia turbolenta il primo e dato da P , produzione di energia turbo-lenta per unita di massa, ed il secondo e ovviamente dato da ε, dissipazionedi energia turbolenta per unita di massa. Meno evidente e il significato deitermini di produzione nell’equazione di bilancio per ε. I valori raccoman-dati per le cinque costanti arbitrarie del modello standard [4] Kt − ε sonoriportati in tabella (2)

13

cµ σk σε cε1 cε20.09 1.0 1.3 1.44 1.92

Table 2: Costanti modello Kt − ε

References

[1] O. Reynolds; On the dynamical theory of incompressible viscous fluidsand the determination of the criterion, Philos. Trans. Roy. Soc. A 186,pp. 123-164, (1895)

[2] J. Boussinesq; Essai sur la theorie des eaux courantes, Mem. pres. pardiv. savants a l’Acad. Sci. 23, 1-680, (1877)

[3] H. Tennekes, J. L. Lumley; A First Course in Turbulence The MITPress Cambridge (1972)

[4] V. C. Patel, W. Rodi, G. Scheuerer; Turbulence models for near-walland low Reynolds number flows : a review, AIAA Journal, 23, pp. 1308-1319, (1985)

14