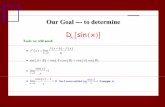
Applications of Trig Functions
of 20
/20
Embed Size (px)
description
Applications of Trig Functions. EQ: How do I use trigonometry in real-life application problems?. Angles of Elevation and Depression. ?. - PowerPoint PPT Presentation
Transcript of Applications of Trig Functions
Applications of Trig Functions
EQ: How do I use trigonometry in real-life application problems?
Angles of Elevation and Depression
4. A closed circuit television camera is mounted on a wall 7.4 feet above a
security desk in an office building. It is used to view an entrance door 9.3 feet
from the desk. Find the angle of depression from the camera lens to the
entrance door.
7.4 feet
?
?9.3 feet
5. The world’s longest escalator is the Leningrad Underground in Lenin Square. The escalator has an angle of elevation of
10.36° and a vertical rise of 195.8 ft. Find the length of the escalator.
195.8 feet
10.36°
?
6. Find the height of a flagpole which casts a shadow of 9.32 m when the sun makes and angle of 63 to the
horizontal.
9.32 m
63
63
?
7. A train must climb at a constant gradient of 5.5 m for every 200 m of
track. Find the angle of incline.
200 m5.5 m
?
8. Find , the pitch of the roof.
Trigonometry and 3-D Figures
EQ: How do you find trigonometric ratios to find
unknown sides and angles in 3-D figures?
9. In the triangular prism, find DF and the angle AFD.
10. All edges of a square-based pyramid are 10 cm in length. Find the angle between the slant edge and a
base diagonal.
11. Find the angle between QW and the base of the 3-D figure.
12. Find the angle PV makes with QV.
13. A symmetric square-based pyramid has base lengths of 6cm and
height of 8cm as shown. Find the measure of the face TQR and the base
Areas of Triangles
EQ: How do you find the area of a triangle using
trigonometry?
Review
What happens if you don’t know the height???
There are some cases where you don’t need the height to find the
area…
What happens if you don’t know the height???
There are some cases where you don’t need the height to find the
area…You have two sides and the
included angle
Labeling a TriangleIf you have a triangle ABC with
angles A, B, C the sides opposite these angles are a, b, c
Formula for the Area of a Triangle when you have 2 sides and the
included angle.
The area of triangle is half of the product of two sides and the sine
of the included angle
Find the area of the triangle:
