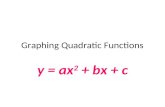2.5 Graphing Quadratic Functions

There are two main methods for graphing a quadratic

I. From Standard Form f (x) = ax2 + bx + c

Axis of Symmetry:

Vertex:

y-int: (when x = 0)

x-int: (when y = 0) set = 0 & solve

2

bx

a

(aka parabola)

,2 2

b bf

a a

0, 0f

(s1, 0) (s2, 0)

Ex 1) f (x) = 3x2 – 9x –12

a) Axis of Symmetry:

b) Vertex:

c) y-int: (0, ??)

( 9) 9 3

2 2(3) 6 2

bx

a

3

2x

3,??

2

23 3 3

3 9 122 2 2

f

9 27 27 273 12 12

4 2 4 2

27 54 48 75

4 4 4 4 3 75

,2 4

20 3 0 9 0 12 12f (0, –12)

Ex 1) f (x) = 3x2 – 9x –12 cont…

d) x-int: (??, 0)

e) Graph

(4, 0) and (–1, 0)

0 = 3x2 – 9x –120 = 3(x2 – 3x –4)0 = 3(x – 4)(x + 1)x = 4, –1

3 75,

2 4

(0, –12)

from prev:

Ex 2) Finding zeros using calculator f (x) = 4x2 – 13x + 5

y = type in 4x2 – 13x + 5

2nd CALC

push graph

arrow over to right of it & hit ENTER

ENTER again

do same for other int

2: zeroput cursor on left side & hit ENTER

0.446 & 2.804

II. From Vertex Form

Change standard to vertex form by completing the square and then use transformations of x2 to graph

Ex 3) Graph f (x) = 2x2 + 12x + 17

f (x) = 2(x2 + 6x ) + 17+ 9

f (x) = 2(x + 3) 2 – 1

The graph of x2 has moved 3 left, 1 down and gotten skinnier by the number 2

– 18

Ex 4) Do it the other way! Write equation from a picture

y = ____(x – ____ ) 2 + ____

vertex: (2 , 4)

y = –2(x – 2) 2 + 4

skinny by 2 a = –2

upside down a is (–)

How???To find ‘a’: plug in a point (1, 2): y = a(x – 2)2 + 4 2 = a(1 – 2)2 + 4–2 = a

Homework

#205 Pg 91 #1–29 odd, 30–35 all, 36, 38, 46