Exponential functions

To explore the properties of exponential functions and their graphs.

To understand the nature and behavior of exponential growth and decay.

To solve problems leading to exponential equations

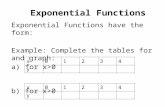
ExponentialFunctions

Inanexponentialfunctiontheunknownappearsintheexponentlikein:

f(x)=2x

Plot the graph of y=2x for 5 x 5

ExponentialFunctions

Inthisgraphasxgetslargerpositivevalues,theyvaluesgetverylarge,itapproachestoinfinity

Forlargernegativevaluesofx,theyvaluesgetsmaller,approachingtozero.Butitneverreacheszero.Wesaythatthexaxisisanasymptotetothegraph

Plot the graph of y=2x for 5 x 5

always increasing

always positive

asymptote:

y-intercept:

OnGDCexplorethegraphsof:

g(x)=3x h(x)=4xf(x)=2x

y=2xy=3xy=4

x

y- intercept:

asymptote:

Plotthegraphof

always decreasing

always positive

asymptote:

y-intercept:

Note: can be written as

Conclusions: y=ax ,a>1

Exponential growth

Asymptote: y=0

y- intercept: (0,1)

the graph is above the x-axis

asiny=2x

Conclusions: y=ax ,0

Exponentialfunctionscanbeusedtomodelreallifesituationsas:growingofaninvestment,ofatumor,ofapopulation,etc.

Thenumberofbacteriainaculture,N,ismodelledbythefunction: N=1000x20.2t,t0wheretismeasuredindays.

Findtheinitialnumberofbacteriaintheculture.

Findthenumberofbacteriaafter5days.

Howlongdoesittakeforthenumberofbacteriatogrowto4000?

1000

2000

10days

UseyourGDCtoplotthegraphofN(t).

Mexico'spopulationisincreasingatarateof2%peryear.CalculatehowlongwillittakeforMexico'spopulationtodouble.

InNigeriathepopulationisincreasingatarateof6.2%peryear.CalculatehowlongwillittakeforNigeria'spopulationtodouble.

ThetemperatureT,indegreesCelsius,ofacoolingliquidismodelledbytheequation:

T=24+72(0.6)3t

wheretisthetimeinminutesafterthecoolingbegins.

a)Whatistheinitialtemperatureoftheliquid?b)Findthetemperatureoftheliquidafter2min.c)Howlongdoesittakefortheliquidtocoolto26oC?d)Whattemperaturedoesthemodelpredicttheliquidwilleventuallyreach?

Wehavebeenworkingwithexamplesofexponentialgrowthanddecayandweuseddifferentbases,baseslike10and2arecommonlyusedformodellingcertainapplications.Howeverthemostimportantbaseisanirrationalnumberdenotedwiththeletter"e".(e2.71828)

Doyouremembertheformulatocalculatecompoundinterest?

A:futurevalueC:initialvaluer:rateofinterestn:numberofperiods

wearegoingtostudywhathappenswhenwecompoundtheinterestcontinuously

wecanwriterasadecimal,thentheformulawillbe:

Ifwecompoundtheinteresttwiceayeartheformulawillbe:

Tosimplifythisstudy,let'smaker=1,C=1

Ifwecompoundtheinterestthreetimesayeartheformulawillbe:

Ifwecompoundtheinteresttwelvetimesayeartheformulawillbe:

wecancontinuetocompoundtheinterestdaily,minutely,secondly...

Usethemenutableinyourcalculatortocomplete:

compounding n

annualsemiannual

quaterly

monthly

daily

hourlyeveryminute

everysecond

12

4

12

365

8760

52560031536000

22.25

2.4414...

2.613035...

2.714567...

2.718126...2.71827921..2.71828247..

Nowmovetothegraphmenuandplotthegraphof

wesaythatthisfunctiontendstonumbere

Wesaythattheexpressiontendstoe:

The irrational number e ( Euler's number)

http://torus.math.uiuc.edu/eggmath/Expon/numbere.html

http://abcnews.go.com/Technology/WhosCounting/story?id=99501&page=1

Therearemanyrealsituationsofcontinuouschange,tomodelthemthemostsuitablefunctionis

Useyourcalculatortodrawthesefunctions.

continuousgrowth

continuousdecay

UseyourGDCtodrawtheexponentialfunction:

Inreallife,thegrowthofbacteriaandothernaturalphenomenasuchaspopulationgrowthfollowanexponentialmodel.

Solvetheequation:

Buteisjustanumber,soitcanbeusedasanyother

Useyourcalculatortofind:

e2 2e1 e2

Solvetheequation:

Solvetheequation:

Solveworksheetexponentialequations

Bookpage48,Ex2Bandpage51Ex2C

ExponentialEquationsandFunctions2014.docx

Y11 EVExponential Equations and Functions

1- NO GDC Solve the following equations

1)

5)

9)

2)

6)

10)

3)

7)

11)

4)

8)

12)

2- No GDC Solve the equations

1

1) 4x - 3 (2 x) + 2=0

2) 25x - 6 ( 5x) +5=0

3) 9x - 10 (3x) +9 =0

4) 25 x 10 (5x)+25 =0

3- No GDC (a) Complete the table..

Function

y-intercept

Increasing or Decreasing

Horizontal asymptote

Root

(b) Sketch each of the functions given in (a). Show clearly all the features found in the table.

4. No GDC Consider the function f(x) = p(0.5)x + q ,where p and q are constants. The graph of f(x) passes through the points (0, 6) and (1, 4) and is shown below.

(a)Write down two equations relating p and q.

(b)Find the value of p and of q.

(c)Write down the equation of the horizontal asymptote to the graph of f(x).

5. No GDC The following diagram shows the graph of y = 3x + 2. The curve passes through the points

(0, a) and (1, b). .

(a)Find the value of

(i)a;(ii)b.

(b)Write down the equation of the asymptote to this curve.

6.No GDC. Consider the function f(x) = 1.25 ax, where a is a positive constant and x 0.The diagram shows a sketch of the graph of f. The graph intersects the y-axis at point A and the line L is its horizontal asymptote.

(a)Find the y-coordinate of A.

The point (2, 1) lies on the graph of y = f(x)

(b)Calculate the value of a.

(c)Write down the equation of L.

7.Shiyun bought a car in 1999. The value of the car V, in USD, is depreciating according to the exponential model

V = 25 000 1.50.2t, t 0,

where t is the time, in years, that Shiyun has owned the car.

(a)Write down the value of the car when Shiyun bought it.

(b)Calculate the value of the car three years after Shiyun bought it. Give your answer correct to two decimal places.

(c)Calculate the time for the car to depreciate to half of its value since Shiyun bought it.

8.A rumour spreads through a group of teenagers according to the exponential model

N = 2 (1.81)0.7t

where N is the number of teenagers who have heard the rumour t hours after it is first started.

(a)Find the number of teenagers who started the rumour.

(b)Write down the number of teenagers who have heard the rumour five hours after it is first started.

(c)Determine the length of time it would take for 150 teenagers to have heard the rumour. Give your answer correct to the nearest minute.

Answers:

1.

2

1. x= 3

2. x= -2

3. x=-2

4. x=-5

5. x= 1/3

6. x=0

7. x=1/3

8. x=2/3

9. x=-11/4

10. x=0, x=2

11. x=-3/2

12. x=-2

2. (1) x= 0, x=1 (2) x= 0, x=1 (3) x= 0, x=3 (4) x=1

4.(a)p + q = 6; 0.5p + q = 4 (b) p = 4, q = 2 (c) y = 2

5.(a)(i)a = 3 (ii) b = 2 (b) y = 2

6.(a)0.25 (b) a = 2 (c) y = 1.25

7.(a) 25 000 USD (b)19 601.32 USD (c) 8.55

8.(a)N = 2 (b) 16.0 (3 s.f.) (c) 624 minutes

SMART Notebook

Attachments

ExponentialEquationsandFunctions2014.docx

Y11 EVExponential Equations and Functions

1- NO GDC Solve the following equations

1)

5)

9)

2)

6)

10)

3)

7)

11)

4)

8)

12)

2- No GDC Solve the equations

1

1) 4x - 3 (2 x) + 2=0

2) 25x - 6 ( 5x) +5=0

3) 9x - 10 (3x) +9 =0

4) 25 x 10 (5x)+25 =0

3- No GDC (a) Complete the table..

Function

y-intercept

Increasing or Decreasing

Horizontal asymptote

Root

(b) Sketch each of the functions given in (a). Show clearly all the features found in the table.

4. No GDC Consider the function f(x) = p(0.5)x + q ,where p and q are constants. The graph of f(x) passes through the points (0, 6) and (1, 4) and is shown below.

(a)Write down two equations relating p and q.

(b)Find the value of p and of q.

(c)Write down the equation of the horizontal asymptote to the graph of f(x).

5. No GDC The following diagram shows the graph of y = 3x + 2. The curve passes through the points

(0, a) and (1, b). .

(a)Find the value of

(i)a;(ii)b.

(b)Write down the equation of the asymptote to this curve.

6.No GDC. Consider the function f(x) = 1.25 ax, where a is a positive constant and x 0.The diagram shows a sketch of the graph of f. The graph intersects the y-axis at point A and the line L is its horizontal asymptote.

(a)Find the y-coordinate of A.

The point (2, 1) lies on the graph of y = f(x)

(b)Calculate the value of a.

(c)Write down the equation of L.

7.Shiyun bought a car in 1999. The value of the car V, in USD, is depreciating according to the exponential model

V = 25 000 1.50.2t, t 0,

where t is the time, in years, that Shiyun has owned the car.

(a)Write down the value of the car when Shiyun bought it.

(b)Calculate the value of the car three years after Shiyun bought it. Give your answer correct to two decimal places.

(c)Calculate the time for the car to depreciate to half of its value since Shiyun bought it.

8.A rumour spreads through a group of teenagers according to the exponential model

N = 2 (1.81)0.7t

where N is the number of teenagers who have heard the rumour t hours after it is first started.

(a)Find the number of teenagers who started the rumour.

(b)Write down the number of teenagers who have heard the rumour five hours after it is first started.

(c)Determine the length of time it would take for 150 teenagers to have heard the rumour. Give your answer correct to the nearest minute.

Answers:

1.

2

1. x= 3

2. x= -2

3. x=-2

4. x=-5

5. x= 1/3

6. x=0

7. x=1/3

8. x=2/3

9. x=-11/4

10. x=0, x=2

11. x=-3/2

12. x=-2

2. (1) x= 0, x=1 (2) x= 0, x=1 (3) x= 0, x=3 (4) x=1

4.(a)p + q = 6; 0.5p + q = 4 (b) p = 4, q = 2 (c) y = 2

5.(a)(i)a = 3 (ii) b = 2 (b) y = 2

6.(a)0.25 (b) a = 2 (c) y = 1.25

7.(a) 25 000 USD (b)19 601.32 USD (c) 8.55

8.(a)N = 2 (b) 16.0 (3 s.f.) (c) 624 minutes

SMART Notebook

Page 1Page 2Page 3Page 4Page 5Page 6Page 7Page 8Page 9Page 10Page 11Page 12Page 13Page 14Page 15Page 16Page 17Page 18Page 19Page 20Page 21Page 22Page 23Page 24Page 25Page 26Page 27Page 28Attachments Page 1